Science and Technology Class 9 Notes Chapter 1 Maharashtra Board

Laws of Motion

Introduction to Motion

What is Motion?

Motion is when an object changes its position with respect to its surroundings. If the position doesn’t change, the object is at rest.

Examples of motion: A flying bird, leaves moving in the air.
Examples of rest: A stationary train, a stone on a hill.

Relative Concept:

Motion depends on your point of view. For example, if you’re in a bus, the person next to you seems still, but both of you are moving relative to the ground. To decide if something is moving, compare it to a fixed point (like the ground or a tree).

Distance and Displacement

Distance:

The total length of the path an object travels from one point to another.
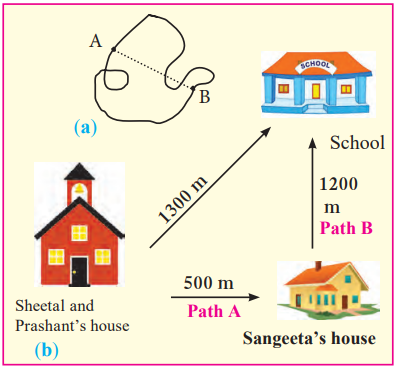
Example: If Sheetal walks 500 m to Sangeeta’s house and then 1200 m to school, her total distance is 1700 m.

Displacement:

The shortest distance between the starting and ending points, in a straight line.
Example: If Sheetal’s house to school is 1300 m straight, her displacement is 1300 m, even if she took a longer path.

Key Difference:

Distance can be more than displacement. If an object returns to its starting point (e.g., a car going from P to Q and back to P), displacement is 0, but distance is not.

Activity Example:

Swaralee walks around a circular field (radius 100 m) for one round.
- Distance = Circumference = 2 × 3.14 × 100 = 628 m.
- Displacement = 0 m (she’s back at the starting point).

Who Reaches Faster?

Sheetal (via Sangeeta’s house: 500 m + 1200 m = 1700 m) takes 29 minutes.
Prashant (straight to school: 1300 m) takes less time because the path is shorter.

Speed and Velocity

Speed:

How fast an object covers distance.
Formula: Speed = Total Distance / Total Time.
Units: m/s (SI system) or cm/s (CGS system).
Example: Sheetal’s average speed = 1700 m / 29 min ≈ 58.6 m/min.

Velocity:

Speed in a specific direction, related to displacement.
Formula: Velocity = Displacement / Time.
Example: Sheetal’s velocity = 1300 m / 29 min ≈ 44.83 m/min (straight-line path).

Difference:

Speed is a scalar (only magnitude).
Velocity is a vector (magnitude + direction).
If motion is straight, speed = velocity; otherwise, they differ.

Effect on Velocity:

Sachin on a motorbike:
1. If speed increases/decreases but direction stays the same, velocity changes in magnitude.
2. On a turn, speed may stay constant, but velocity changes due to direction change.
3. If both speed and direction change on a turn, velocity changes more.

Uniform and Non-Uniform Motion

Uniform Motion:

Object covers equal distances in equal time intervals.
Example: A car moving at a steady 60 km/h.
Graph: Distance-time graph is a straight line (slope shows speed).

Non-Uniform Motion:

Object covers unequal distances in equal time intervals.
Example: A bus in traffic.
Graph: Distance-time graph is a curve (not straight).

Activity:

Roll a ball down a sloped tube. Velocity increases from top to bottom (non-uniform motion).

Acceleration

What is Acceleration?

The rate of change of velocity.
Formula: Acceleration = (Final Velocity – Initial Velocity) / Time = (v – u) / t.
Units: m/s².

Types:

Uniform Acceleration: Velocity changes by equal amounts in equal time intervals (e.g., free fall).
Non-Uniform Acceleration: Velocity changes unevenly (e.g., car in traffic).

Positive and Negative Acceleration:

Positive: Velocity increases (e.g., speeding up).
Negative: Velocity decreases (deceleration, e.g., slowing down).
Zero: Velocity stays the same (no acceleration).

Example:

Sliding down a park slide: Velocity is low at the top, high in the middle, and zero at the bottom.

Distance-Time and Velocity-Time Graphs

Distance-Time Graph:

Uniform Motion: Straight line (e.g., car data: 20 m, 40 m, 60 m in 1, 2, 3 s).

Non-Uniform Motion: Curved line (e.g., bus data varies irregularly).

Slope = Speed.

Velocity-Time Graph:

Uniform Velocity: Horizontal line (e.g., train at 60 km/h for 5 hours).

Distance = Area under the graph (e.g., between 2-4 hours = 60 × 2 = 120 km).

Uniform Acceleration: Straight line (e.g., car velocity increases from 16 to 32 m/s in 5 s).

Distance = Average velocity × Time (e.g., (32 + 16) / 2 × 10 s = 240 m).

Equations of Motion

Derived using velocity-time graphs for uniform acceleration.

First Equation: v = u + at

Relates velocity (v), initial velocity (u), acceleration (a), and time (t).

Second Equation: s = ut + (1/2)at²

Relates displacement (s), initial velocity (u), acceleration (a), and time (t).

Third Equation: v² = u² + 2as

Relates final velocity (v), initial velocity (u), acceleration (a), and displacement (s).

Graphical Method:

Area under the velocity-time graph gives displacement.

Uniform Circular Motion

What is It?

Motion along a circular path at constant speed, but velocity changes due to direction change.
Examples: Tip of a clock’s second hand, a stone in a sling.

Speed Formula:

Speed = Circumference / Time = 2πr / t (where r = radius, t = time for one round).

Activity:

Trace a polygon (square, pentagon) and note direction changes. As sides increase (to infinity), it becomes a circle.

Direction of Velocity:

A coin on a spinning disc flies off tangentially (perpendicular to the radius), showing velocity direction changes continuously.

Newton’s Laws of Motion

First Law (Law of Inertia):

“An object stays at rest or moves straight at a constant speed unless an unbalanced force acts on it.”
Example: A coin on cardboard stays still until the cardboard is hit.
Inertia depends on mass (more mass = more inertia).

Balanced vs. Unbalanced Forces:

Balanced: Forces cancel out (e.g., tug-of-war with equal pull).
Unbalanced: Net force causes motion (e.g., tug-of-war with unequal pull).

Second Law:

“The rate of change of momentum is proportional to the applied force and happens in the force’s direction.”
Formula: F = m × a (Force = Mass × Acceleration).
Momentum (P) = m × v (mass × velocity).
Unit: 1 Newton (N) = 1 kg × 1 m/s².
Example: A heavier ball is harder to catch at the same speed due to more momentum.

Third Law:

“Every action has an equal and opposite reaction.”
Example: A balloon boat moves forward as air escapes backward.
Action and reaction act on different objects, so they don’t cancel.

Law of Conservation of Momentum

Principle:

“Total momentum before and after a collision is the same if no external force acts.”
Example: A bullet and gun-bullet moves forward, gun recoils backward, total momentum = 0.

Formula:

m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂ (initial momentum = final momentum).

Examples:

Cannon recoil: 500 kg cannon at 0.25 m/s = 125 kg m/s momentum.
Two balls colliding: Momentum redistributes based on masses and velocities.