मराठी इयत्ता १० वी Chapter 1 गुरुत्वाकर्षण Vigyan Solution महाराष्ट्र Board Marathi

स्वाध्याय

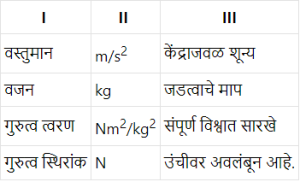
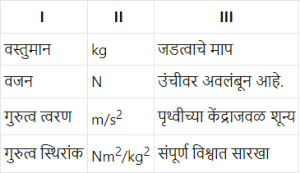
Q १. खालील तक्त्यातील तीनही स्तंभातील नोंदी मधील संबंध लक्षात घेऊन त्याप्रमाणे तक्ता परत लिहा.

उत्तरे.

Q २. खालील प्रश्नांची उत्तरे लिहा.

अ. वजन व वस्तुमान यातील फरक काय आहे? एखाद्या वस्तूचे पृथ्वीवरील वस्तुमान व वजन मंगळावरही तेवढेच असतील का? का?

उत्तरे. वस्तूचे वस्तुमान पृथ्वीवर व मंगळावर समान असेल, परंतु वजन मात्र समान नसेल, कारण g चे मंगळावरील मूल्य पृथ्वीवरील g च्या मूल्यापेक्षा वेगळे आहे.

आ. मुक्त पतन, गुरुत्व त्वरण, मुक्ति वेग व अभिकेंद्री बल म्हणजे काय?

उत्तरे. एखादी वस्तू केवळ गुरुत्वीय बलाच्या प्रभावाने गतिमान असल्यास त्या गतीला मुक्त पतन म्हणतात.

पृथ्वीच्या (अथवा इतर ग्रहाच्या/उपग्रहाच्या/ताऱ्याच्या) गुरुत्वीय बलामुळे वस्तूचे त्वरण होते. या त्वरण पृथ्वीचे (अथवा त्या ग्रहाचे/उपग्रहाचे/ताऱ्याचे) गुरुत्व त्वरण म्हणतात.

ज्या विशिष्ट आरंभ वेगामुळे पृथ्वीच्या (अथवा इतर ग्रहाच्या/उपग्रहाच्या/ताऱ्याच्या) पृष्ठभागापासून सरळ वर जाणारी वस्तू पृथ्वीच्या (अथवा त्या ग्रहाच्या/उपग्रहाच्या/ताऱ्याच्या) गुरुत्वाकर्षणापासून मुक्त होते त्यास मुक्तिवेग म्हणतात. या वेळी वस्तू पृथ्वीपासून (अथवा त्या ग्रहापासून/उपग्रहा पासून/ताऱ्यापासून) अनंत अंतरावर जाऊन स्थिर होईल.

वर्तुळाकार कक्षेत फिरणाऱ्या कोणत्याही वस्तूवर वर्तुळाच्या केंद्राच्या दिशेने बल प्रयुक्त होत असते. या बलास अभिकेंद्री बल म्हणतात.

इ. केप्लरचे तीन नियम लिहा. त्यामुळे न्यूटनला आपला गुरुत्व सिद्धांत मांडण्यात कशी मदत झाली?

उत्तरे.  केप्लरचा पहिला नियम: ग्रहाची कक्षा ही लंब-वर्तुळाकार असून, सूर्य त्या कक्षेच्या एका नाभीवर असतो.

पुढील आकृतीमध्ये एका ग्रहाची सूर्याभोवतीच्या परिभ्रमणाची लंबवर्तुळाकार कक्षा दाखवली आहे. सूर्याची स्थिती S ने दाखवली आहे.

ग्रहाची सूर्याभोवतीची परिभ्रमण कक्ष (प्रारूप आकृती)

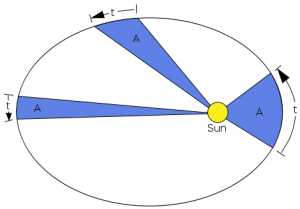
केप्लरचा दुसरा नियम: ग्रहाला सूर्याशी जोडणारी सरळ रेषा, ही समान कालावधीत समान क्षेत्रफळ व्यापन करते.
समान कालावधीत ग्रहाचे विस्थापन A → B, C → D, E → F असे होते. आकृतीमधील ASB, CSD व ESF ही क्षेत्रफळे समान आहेत.

केप्लरचा तिसरा नियम: सूर्याची परिक्रमा करणाऱ्या ग्रहाच्या आवर्तकालाचा वर्ग हा ग्रहाच्या सूर्यापासूनच्या सरासरी अंतराच्या घनाला समानुपाती असतो. म्हणजे ग्रहाचा आवर्तकाल T असेल व सूर्यापासून ग्रहाचे सरासरी अंतर r असेल, तर T2 ∝ r3 , म्हणजेच ., `”T”^2/”r”^3` स्थिर = K ……(1)

ग्रहाची सूर्याभोवतीची वर्तुळाकार गती

समजा एक वस्तू एकसमान वर्तुळाकार गतीने गतिमान आहे. अशा प्रकारे गतिमान असलेल्या वस्तूवर केंद्राकडे निर्देशित अभिकेंद्री बल प्रयुक्त होत असते, हे आपण पाहिले. या वस्तूचे वस्तुमान m ने, तिच्या कक्षेची त्रिज्या r ने व तिची चाल v ने दर्शविली तर या बलाचे परिमाण `”mv”^2/”r”` एवढे असते, हे गणिती क्रियेद्वारे दाखवता येते.

आता जर एक ग्रह वर्तुळाकार कक्षेत सूर्याची परिक्रमा करत असेल तर त्यावर सूर्याच्या दिशेने प्रयुक्त होणारे अभिकेंद्री बल F = `”mv”^2/”r”` असले पाहिजे. येथे m हे ग्रहाचे वस्तुमान, v ही त्याची चाल व r ही ग्रहाच्या वर्तुळाकार कक्षेची त्रिज्या म्हणजेच ग्रहाचे सूर्यापासूनचे अंतर आहे. त्याची चाल आपण त्याचा आवर्तकाल (T) म्हणजे सूर्याभोवती एक परिक्रमा करण्याचा कालावधी व त्रिज्या वापरून काढू शकतो.

ग्रहाने एका परिक्रमेत पार केलेले अंतर = कक्षेचा परीघ = 2πr ; r = सूर्यापासूनचे अंतर , त्यासाठी लागलेला वेळ = आवर्त काल = T

v = कक्षेचा परिघ/आवर्त काल = `(2pi”r”)/”T”`

F = `”mv”^2/”r” = (“m”((2pi”r”)/”T”)^2)/”r” = (4 “m” pi^2 “r”)/”T”^2`, ह्यास r2 ने गुणल्यावर व भागल्यावर आपल्यास मिळते की, F = `(4 “m” pi^2)/”r”^2 (“r”^3/”T”^2)` केप्लरच्या तिसऱ्या नियमा प्रमाणे `”T”^2/”r”^3` = K हे स्थिर असते. म्हणून F = `(4 “m” pi^2)/(“r”^2 “K”)` पण `(4″m”pi^2)/”K”` = स्थिर, म्हणून F ∝ `1/”r”^2`

म्हणजे सूर्य व ग्रह यामधील अभिकेंद्री बल, जे ग्रहाच्या परिभ्रमणास कारणीभूत असते, ते त्यांच्यामधील अंतराच्या वर्गाच्या व्यस्त प्रमाणात असते. हेच गुरुत्वीय बल असून ते अंतराच्या वर्गाच्या व्यस्त प्रमाणात असते असा न्यूटनने निष्कर्ष काढला. गुरुत्वाकर्षणाचे बल हे निसर्गातील इतर बलांच्या तुलनते अत्यंत क्षीण असते परंतु ते संपूर्ण विश्वाचे नियंत्रण करते व विश्वाचे भवितव्य निश्चित करते. ग्रह, तारे व विश्वातील इतर घटक ह्यांच्या प्रचंड वस्तुमानांमुळे हे शक्य होते.

ई. एक दगड u वेगाने वर फेकल्यावर h उंची पर्यंत पोचतो व नंतर खाली येतो. सिद्ध करा की त्याला वर जाण्यास जितका वेळ लागतो तितकाच वेळ खाली येण्यास लागतो.

उत्तरे. गतीविषयक समीकरणे: