Solutions For All Chapters – गणित Class 6
Ex 12.1 – बीजगणित
प्रश्न 1. तीलियों से निम्न प्रतिरूप बनाने के लिए आवश्यक तीलियों की संख्या के लिए नियम ज्ञात कीजिए। नियम लिखने के लिए एक चर का प्रयोग कीजिए :
हल :
(a) U के लिए:
उपरोक्त आकृति से स्पष्ट है कि एक U बनाने में 3 माचिस की तीलियों का प्रयोग किया गया है।
अतः नियम होगा :
वांछित माचिस की तीलियों की संख्या = 3n, जहाँ n का मान 1, 2, 3….. ले सकते हैं।
(b) Z के लिए:
उपरोक्त आकृति से स्पष्ट है कि एक Z बनाने में 3 माचिस की तीलियों का प्रयोग किया गया है।
अत: नियम होगा :
वांछित माचिस की तीलियों की संख्या = 3n, जहाँ n का मान 1, 2, 3….. ले सकते हैं।
(c) B के लिए :
उपरोक्त आकृति से स्पष्ट है कि एक B बनाने में 5 माचिस की तीलियों का प्रयोग किया गया है।
अतः नियम होगा :
वांछित माचिस की तीलियों की संख्या = 5n, जहाँ n का मान 1, 2, 3,…..ले सकते हैं।
(d) S के लिए :
उपरोक्त आकृति से स्पष्ट है कि एक S बनाने में 5 माचिस की तीलियों का प्रयोग किया गया है।
अतः नियम होगा :
वांछित माचिस की तीलियों की संख्या = 5n, जहाँ n का मान 1, 2, 3….. ले सकते हैं।
(e) A के लिए:
उपरोक्त आकृति से स्पष्ट है कि एक A बनाने में 6 माचिस की तीलियों का प्रयोग किया गया है।
अतः नियम होगा :
वांछित माचिस की तीलियों की संख्या = 6n, जहाँ n का मान 1, 2, 3….. ले सकते हैं।
प्रश्न 2. गणतंत्र दिवस के अवसर पर बच्चे मुख्य अतिथि के सम्मुख सामूहिक ड्रिल का प्रदर्शन कर रहे हैं। एक पंक्ति में 10 बच्चे हैं। यदि पंक्तियों की संख्या ज्ञात हो, तो बच्चों की संख्या प्राप्त करने के लिए क्या नियम है? (पंक्तियों की संख्या के लिए a का प्रयोग कीजिए)।
हल : यदि पंक्तियों की संख्या मानलिया जाए तथा एक पंक्ति में बच्चों की संख्या 10 हो तो तो बच्चों की संख्या प्राप्त करने के लिए नियम 10a होगा।
प्रश्न 3. एक टोकरी में 60 केले हैं आप टोकरियों की संख्या के पदों में केले की कुल संख्या को किस प्रकार लिखेंगे? टोकरियों की संख्या के लिए b का प्रयोग कीजिए-
हल :
एक टोकरी में केले की संख्या 60 है।
और मान लिया कि टोकरियों की संख्या b है।
तब टोकरियों की संख्या के पदों में केले की कुल संख्या 60 × b = 60b होगी।
प्रश्न 4. लोकेश अपनी कक्षा के प्रत्येक विद्यार्थी को जन्म दिन के उपलक्ष्य पर 2 टॉफियाँ बाँटता है। विद्यार्थियों की संख्या ज्ञात होने पर क्या आप कुल टॉफियों की संख्या बता सकते हैं? विद्यार्थियों की संख्या के लिए m का प्रयोग कीजिए।
हल :
प्रत्येक विद्यार्थी को 2 टॉफी दिया जाता है।
माना कि विद्यार्थियों की संख्या m हो, तब,
विद्यार्थियों की संख्या m होने पर आवश्यक टॉफियों की संख्या 2 × m = 2m होगी।
प्रश्न 5. सीमा गुड़िया की बड़ी बहन है। सीमा गुड़िया से 5 वर्ष बड़ी है
(a) क्या आप सीमा की आयु :गुड़िया की आयु के पदों में लिख सकते हैं?
(b) क्या आप गुड़िया की आयु सीमा की आयु के पदों में लिख सकते हैं?
हल : माना कि गुड़िया की आयु x वर्ष हो तब
(a) तब सीमा की आयु गुड़िया से 5 वर्ष अधिक है।
सीमा की आयु = (x + 5) वर्ष।
अतः सीमा की आयु गुड़िया की आयु के पदों में (x + 5) वर्ष होगी।
(b) माना कि सीमा की आयु वर्ष है
प्रश्न से सीमा गुड़िया से 5 वर्ष बड़ी है
सीप की आयु = गुड़िया की आयु + 5
y = गुड़िया की आयु + 5
गुड़िया की आयु = y – 5
प्रश्न 6. अमरुद की बड़ी टोकरियों में से छोटी टोकरियों में अमरुद को रखा जाना है। जब एक बड़ी टोकरी को खाली किया जाता है तो उसके अमरुदों से तीन छोटी टोकरियाँ भर जाती है और फिर भी 25 अमरुदें शेष रह जाते हैं। यदि एक छोटी टोकरी में अमरुदों की संख्या को x लिया जाय, तो बड़ी। टोकरी में अमरुदों की संख्या क्या है?
हल : माना कि यदि एक छोटी टोकरी में अमरुदों की संख्या x लिया जाय तो 3 छोटी टोकरियों में अमरुदों की संख्या 3x होगी
प्रश्न से, एक बड़ी टोकरी में अमदों की संख्या = 3 × x + 25
अर्थात् 3x + 25 होगी।
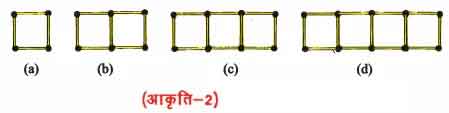
प्रश्न 7. (a) अलग-अलग लम्बाई के तीलियों से बने हुए आयतों के नीचे दिए हुए प्रतिरूपों को देखिए (अकृति 2) ये आयत अलग-अलग नहीं है। दो संलग्न आयतों में एक तं नी उभयनिष्ठ है। इस प्रतिरूप को देखिए और वह नियम ज्ञात कीजिए जो आयतों की संख्या के पदों में आवश्यक तीलियों की संख्या देता है।
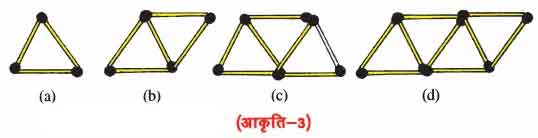
(b) तीलियों से त्रिभुजों का एक प्रतिरूप (आकृति-3) दर्शा रही है उपरोक्त प्रश्न 7(a) की तरह वह व्यापक नियम ज्ञात कीजिए जो त्रिभुज की संख्या के पदों में आवश्यक तीलियों की संख्या देता है।
हल :
(a) एक आयत को बनाने में आवश्यक तीलियों की संख्या 4 होती है जबकि दो आयत के बनाने में आवश्यक तीलियों की संख्या 7 होती है क्योंकि ये दोनों आयत अलग-अलग नहीं हैं ये आयत संलग्न है जिसके कारण एक तीली उभयनिष्ठ है । उभयनिष्ठ होने के कारण दो आयत बनाने पर एक तीली की संख्या कम हो जाती है। तथा 7 को (2 × 4 – 1) लिख सकते हैं।
तीन आयत बनाने में दो तीली उभयनिष्ठ होती है जिसके कारण इन्हें बनाने में आवश्यक तीलियों की संख्या 10 होती है। 10 को (3 × 4 – 2)
चार आयत बनाने में तीन तीलियाँ उभयनिष्ठ होती है जिसके कारण इन्हें बनाने में आवश्यक तीलियों की संख्या 13 अर्थात् (4 × 4 – 3) होती है।
इस प्रकार हम देखते हैं कि n उभयनिष्ठ आयत को बनाने के लिए आवश्यक तीलियों की संख्या {n × 4 – (n – 1)}
= 4n – n + 1 = 3n + 1 होता है।
(b) एक त्रिभुज बनाने के लिए आवश्यक तीलियों की संख्या 3 होती है। दो त्रिभुज बनाने पर एक तीली उभयनिष्ठ हो जाने के कारण तीलियों की संख्या 5 अर्थात् (2 × 3 – 1) होती है।
तीन त्रिभुज बनाने पर तीली उभयनिष्ठ हो जाने के कारण तीलियों की संख्या 7 अर्थात (3 × 3 – 2) होती है।
चार त्रिभुज बनाने पर तीन तीलियाँ उभयनिष्ठ हो जाने के कारण तीलियों की संख्या 9 अर्थात् (4 × 3 – 3) होती है।
इस प्रकार हम देखते हैं कि n उभयनिष्ठ त्रिभुजों को बनाने के लिए आवश्यक तीलियों की संख्या {n × 3 – (n – 1)}
अर्थात् (3n – n + 1) = 2n + 1 होगा।


Very Good