Notes For All Chapters Maths Class 10 CBSE
Circle: A circle is a collection of all points in a plane which are at a constant distance from a fixed point.
Centre: The fixed point is called the centre.
Radius: The constant distance from the centre is called the radius.
Chord: A line segment joining any two points on a circle is called a chord.
Diameter: A chord passing through the centre of the circle is called diameter. It is the longest chord.
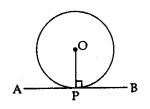
Tangent: When a line meets the circle at one point or two coincidings The line is known as points, a tangent.
The tangent to a circle is perpendicular to the radius through the point of contact.
⇒ OP ⊥ AB
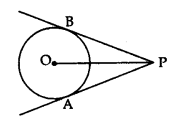
The lengths of the two tangents from an external point to a circle are equal.
⇒ AP = PB
Length of Tangent Segment
PB and PA are normally called the lengths of tangents from outside point P.
Properties of Tangent to Circle
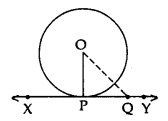
Theorem 1: Prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
Given: XY is a tangent at point P to the circle with centre O.
To prove: OP ⊥ XY
Construction: Take a point Q on XY other than P and join OQ
Proof: If point Q lies inside the circle, then XY will become a secant and not a tangent to the circle
OQ > OP
This happens with every point on the line XY except the point P. OP is the shortest of all the distances of the point O to the points of XY
OP ⊥ XY …[Shortest side is the perpendicular]
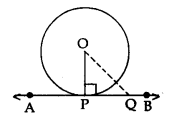
Theorem 2: A line drawn through the end point of a radius and perpendicular to it, is the tangent to the circle.
Given: A circle C(O, r) and a line APB is perpendicular to OP, where OP is the radius.
To prove: AB is tangent at P.
Construction: Take a point Q on the line AB, different from P and join OQ.
Proof: Since OP ⊥ AB
OP < OQ ⇒ OQ > OP
The point Q lies outside the circle.
Therefore, every point on AB, other than P, lies outside the circle.
This shows that AB meets the circle at point P.
Hence, AP is a tangent to the circle at P.
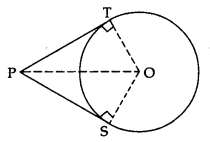
Theorem 3: Prove that the lengths of tangents drawn from an external point to a circle are equal
Given: PT and PS are tangents from an external point P to the circle with centre O.
To prove: PT = PS
Construction: Join O to P, T and S.
Proof: In ∆OTP and ∆OSP.
OT = OS …[radii of the same circle]
OP = OP …[common]
∠OTP = ∠OSP …[each 90°]
∆OTP = ∆OSP …[R.H.S.]
PT = PS …[c.p.c.t.]
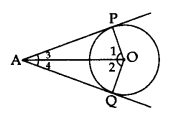
Note: If two tangents are drawn to a circle from an external point, then:
- They subtend equal angles at the centre i.e., ∠1 = ∠2.
- They are equally inclined to the segment joining the centre to that point i.e., ∠3 = ∠4.
∠OAP = ∠OAQ

Leave a Reply