Electricity
Solutions For All Chapters Science 10 CBSE
NCERT TEXTBOOK Solutions for Class 10 Science
1. A piece of wire of resistance R is cut into five equal parts. These parts are then connected in parallel. If the equivalent resistance of this combination is R′, then the ratio R/R′ is –
(a) 1/25
(b) 1/5
(c) 5
(d) 25
Answer: (d) 25
2. Which of the following terms does not represent electrical power in a circuit?
(a) I2R
(b) IR2
(c) VI
(d) V2 / R
Answer:
(b)IR2
3. An electric bulb is rated 220 V and 100 W. When it is operated on 110 V, the power consumed will be –
(a) 100 W
(b) 75 W
(c) 50 W
(d) 25 W
Answer: (d) 25 W
4. Two conducting wires of the same material and of equal lengths and equal diameters are first connected in series and then parallel in a circuit across the same potential difference. The ratio of heat produced in series and parallel combinations would be –
(a) 1:2
(b) 2:1
(c) 1:4
(d) 4:1
Answer: (c) 1:4
Q5. How is a voltmeter connected in the circuit to measure the potential difference between two points?
Answer: A voltmeter is always connected in parallel to the component across which potential difference is to be measured.
Q6. A copper wire has diameter 0.5 mm and resistivity of 1.6 × 10⁻⁸ Ω m. What will be the length of this wire to make its resistance 10 Ω? How much does the resistance change if the diameter is doubled?
Answer:
We know the formula for resistance:
ρ=1.6× 10-8 Ωm
𝑅=10 Ω
diameter 𝑑=0.5 mm = 0.0005 m
d=0.5 mm=0.0005 m,
radius 𝑟 = \(\frac{d}{2}\) =0.00025
So the cross-sectional area:
A=π r2 =π(0.00025)2 =1.963× 10-7 m2
Now,
l=122.7 m (approximately 123 m)
If the diameter is doubled:
New diameter
𝑑′=2×0.5 mm=1 mm=0.001 m
New radius
𝑟′=0.0005 m
New area:
A′= π (0.0005)2 = 7.854 × 10-2 m2
So,
Final Result:
Required length of wire = 123 m (approx.)
Resistance when diameter is doubled = 2.5 Ω
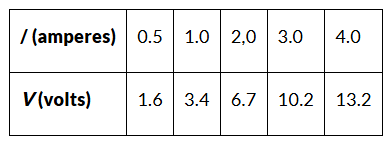
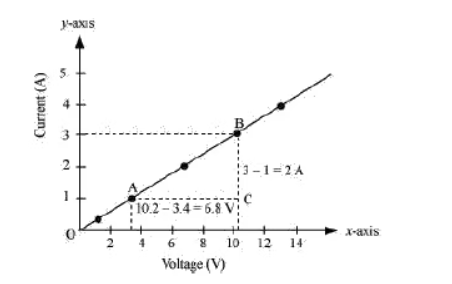
Q 7. The values of current I flowing in a given resistor for the corresponding values of potential difference V across the resistor are given below –
Answer: Plot a graph between V and I and calculate the resistance of that resistor. The plot between voltage and current is called IV characteristic. The voltage is plotted on x-axis and current is plotted on y-axis. The values of the current for different values of the voltage are shown in the given table
The IV characteristic of the given resistor is plotted in the following figure.
The slope of the line gives the value of resistance (R) as,
Therefore, the resistance of the resistor is 3.4 Ω.
Q8. When a 12 V battery is connected across an unknown resistor, there is a current of 2.5 mA in the circuit. Find the value of the resistance of the resistor.
Answer: We are given:
Potential difference, V = 12 V
Current, I = 2.5 mA = 2.5 × 10⁻³ A
Using Ohm’s Law:
The resistance of the resistor is 4800 Ω (4.8 kΩ).
Q 9. A battery of 9 V is connected in series with resistors of 0.2 Ω, 0.3 Ω, 0.4 Ω, 0.5 Ω and 12 Ω, respectively. How much current would flow through the 12 Ω resistor?
Answer: Since all the resistors are connected in series, the total resistance is the sum of all individual resistances.
R=0.2+0.3+0.4+0.5+12
R=13.4 Ω
The total potential difference of the battery is
V=9 V
Using Ohm’s Law:
In a series circuit, the same current flows through all resistors.
Therefore, the current through the 12 Ω resistor is also 0.67 A.
Q 10. How many 176 Ω resistors (in parallel) are required to carry 5 A on a 220 V line?
Answer: –
We are given:
Voltage, 𝑉=220
Current, 𝐼=5
Resistance of each resistor, 𝑅=176Ω
First, find the equivalent resistance required for the circuit using Ohm’s law:
Now, for n,resistors of resistance R connected in parallel
4 resistors of 176 Ω in parallel are required.
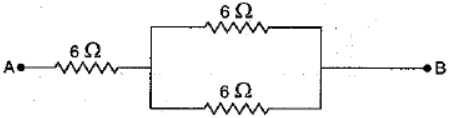
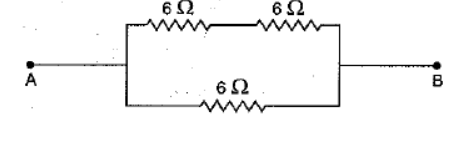
Q11: Show how you would connect three resistors, each of resistance 6 Ω so that the combination has a resistance of (i) 9 Ω, (ii) 4 Ω.
Ans: (i) When two 6 Ω resistances are in parallel and the third is in combination with this, the equivalent resistance will be 9Ω.
(if) When two 6 Ω resistances are in series and the third is in parallel to them, then it will be 4 Ω.
Q 12.Several electric bulbs designed to be used on a 220 V electric supply line, are rated 10 W. How many lamps can be connected in parallel with each other across the two wires of 220 V line if the maximum allowable current is 5 A?
Answer: Power of each lamp = 10 W
Supply voltage = 220 V
Current drawn by each lamp:
Maximum allowable current = 5 A
Number of lamps that can be connected in parallel:
Therefore, 110 lamps can be connected in parallel.
Q 12. A hot plate of an electric oven connected to a 220 V line has two resistance coils A and B, each of 24 Ω resistance, which may be used separately, in series, or in parallel. What are the currents in the three cases?
Answer: Resistance R1 of the bulb is given by the expression:
R1= \(\frac{V^2}{P}\)
Supply voltage, 𝑉=220
Maximum allowable current, 𝐼=5
Rating of each bulb, P=10W
R1=\(\frac{220^2}{10}\) =4840Ω
According to Ohm’s law,
V=IR
Let R be the total resistance of the circuit for 𝑥 number of electric bulbs.
Since the bulbs are connected in parallel,
R=\(\frac{r_1}{𝑥}\) =4840Ω
Q13. A hot plate of an electric oven connected to a 220 V line has two resistance coils A and B, each of 24 Ω resistance, which may be used separately, in series, or in parallel. What are the currents in the three cases?
Answer: Given , \( R_A -R_B \) = 24 Ω . Use Ohm’s law I = \(\frac{V}{R}\).
(A) One coil used separately
Here the resistance R=24 Ω
I=\(\frac{220}{24}\) =9.1666… A≈9.17 A
(B) Two coils in series
Equivalent resistance \( R_Series \) =24+24=48 Ω.
I = \(\frac{220}{48}\)=4.5833… A≈4.58 A
(C) Two coils in parallel
\(\frac{1} R_parallel \) = \(\frac{1}{24}\) + \(\frac{1}{24}\)–\(\frac{1}{12}\) =\( R_parallel \) =12 Ω
I = \(\frac{220}{12}\) =18.3333… A≈18.33 A
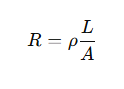
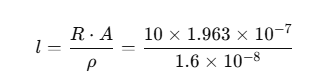
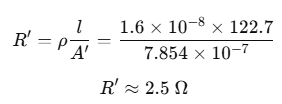
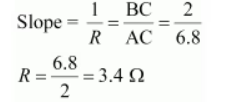
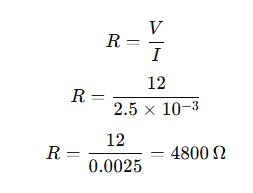
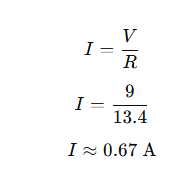
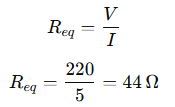
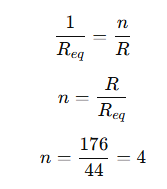
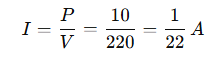
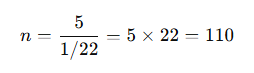
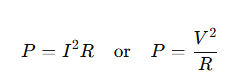
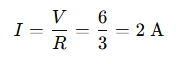
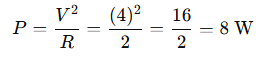

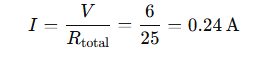
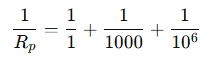
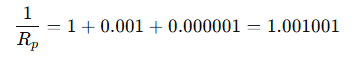
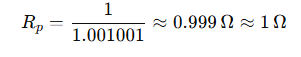

Leave a Reply