Applications Of Integrals, Class 12 Mathematics R.D Sharma Solutions

Page 21.13 Ex.21.1

Q1.

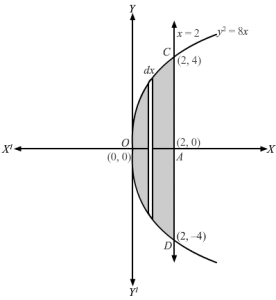
y2=8x represents a parabola with vertex at origin and axis of symmetry along the +ve direction of x-axisx=2 is line parallel to y-axisLet (x, y) be a given point on the parabola , y2=8xSince parabola y2=8x is symmetric about x-axis ,∴Required area =2 area OCAO On slicing the area above x-axis into vertical strips of length =y and width =dx ⇒area of rectangular strip=y dxThe approximating rectangle moves between x=0 and x=2. So, area A=2 area OCAO⇒A=2∫02y dx=2∫02y dx as y>0 ⇒A=2∫028x dx ⇒A=2×2∫022x dx= 42∫02x dx⇒A= 42 x323202=832 232-0 =83×22=323 sq. units∴ Area A=323 sq. units

Q2.

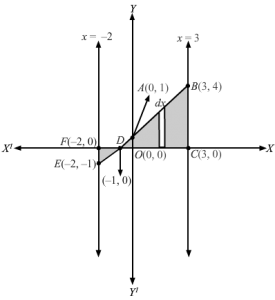
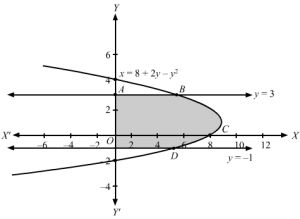
∵ y-1 =x is a straight line cutting x-axis at D(-1, 0) and y-axis at A( 0, 1) And, x=-2 and x=3 are straight lines parallel to y-axis Also, since y =-1+x, for x≤-1And y = 1+x, x>-1∴ Area of region bound by line y-1=x , x axis and the ordinates x=-2 and x=3 isArea A = area FED+area DOA +area OABC⇒A=∫-23y dx⇒A=∫-2-1y dx +∫-10y dx +∫03y dx⇒A=∫-2-1-1+x dx +∫-101+x dx+∫031+x dx⇒A=-x+x22-2-1+x+x22-10+x+x2203⇒A=1-12-2+42+0+1-12+3+92⇒A=-1+32+1-12+3+92=3+3-1+92=3+112=172 sq. units∴Area of the bound region =172 sq. units

Q3.

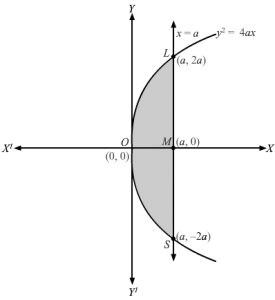
The equation y2=4ax represents a parabola, with vertex at (0, 0) and symmetric about positive side of x-axis x=a is a line parallel to y-axis , and cutting x-axis at (a, 0)Making vertical strips of length =y and width=dx in the quadrant OLSO.Area of approximating rectangle =y dxSince the approximating rectangle can move between x=0 and x=a ,and as the parabola is symmetric about x-axis ,Required shaded area OLSO=A=2× Area OLMOA= 2∫0ay dx=2∫0ay dx As, y>0⇒y =y⇒A=2∫0a4ax dx⇒A=4∫0aax dx⇒A=4a∫0ax dx⇒A=4a x32320a⇒A=83aa32-0⇒A=83a2 sq. units

Page 21.14 Ex.21.1

Q4.

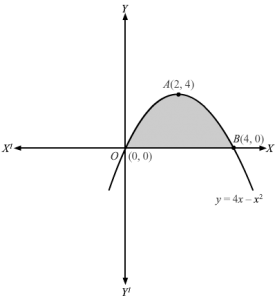
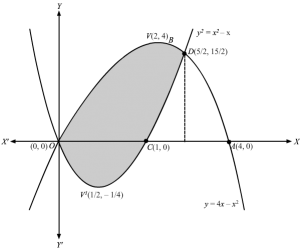
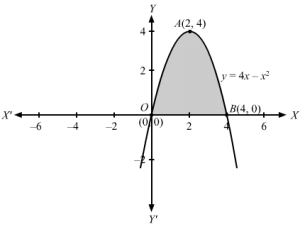
The equation y=4x-x2 represents a parabola opening downwards and cutting the x axis at O(0, 0) and B(4, 0)Slicing the region above x axis in vertical strips of length= y and width =dx , area of corresponding rectangle is = y dxSince the corresponding rectangle can move from x=0 to x=4,∴Required area OABO isA=∫04y dx= ∫04y dx As, y>0 for 0≤ x≤ 4 ⇒ y =y⇒ A=∫044x-x2 dx ⇒ A=4×22-x3304⇒ A=32-643⇒ A=323 square units

Q5.

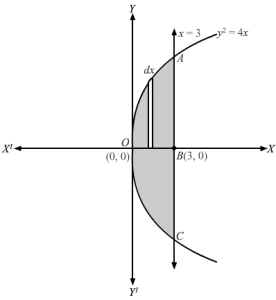
y2=4x represents a parabola with vertex at (0, 0) and axis of symmetry along the +ve direction of x axis x=3 is a line parallel to y axis and cutting x axis at (3, 0)Since y2=4x is symmetrical about x axis , ∴Required area A=OA CO=2× area OABOSlicing the area above x axis into vertical strips of length=y and width = dx Area of corresponding rectangle= y dxThe corresponding rectangle moves from x=0 to x=3A=2× area OABO⇒A=2∫03 y dx= 2∫03 y dx As, y=y, y>0⇒A= 2∫034x dx ⇒A=4∫03x dx ⇒A=4×323203= 83×3203=83×33=83 sq. units∴Area of region bound by curve y2=4x and x=3 is 83 sq. units

Q6.

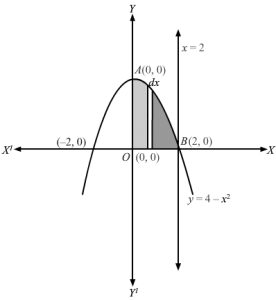
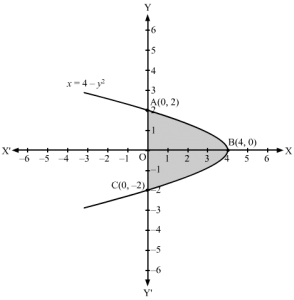
y=4-x2, 0≤x≤2 represents a half parabola with vetex at (4, 0) x=2 represents a line parallel to y-axis and cutting x-axis at (2, 0) In quadrant OABO, consider a vertical strip of length= y, width=dx∴Area of approximating rectangle= y dx The approximating rectangle moves from x=0 to x=2⇒A=Area OABO =∫02 y dx ⇒A=∫02 y dx As, y>o, y =y⇒A=∫024-x2 dx ⇒A=4x-x3302⇒A=8-83⇒A=163 sq. units∴The area enclosed by the curve and x-axis and given lines =163 sq. units

Q7.

y=x+1 in 0, 4 represents a curve which is part of a parabola x=4 represents a line parallel to y-axis and cutting x-axis at (4, 0)Enclosed area bound by the curve and lines x=0 and x=4 is OABCOConsider a vertical strip of lenght =y and width=dx∴Area of approximating rectangle= y dxThe approximating rectangle moves from x=0 to x=4⇒A=Area OABCO=∫04y dx⇒A=∫04y dx y>0⇒y =y⇒A=∫04x+1 dx⇒A=∫04x+112 dx⇒A=x+1323204⇒A=23532-1 sq. units∴ Enclosed area between the curve and given lines =23532-1 sq. units

Q8.

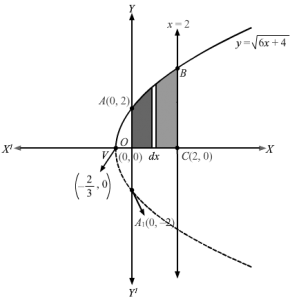
y=6x+4 represents a parabola, with vertex V(-23, 0) and symmetrical about x-axis x=0 is the y-axis . The curve cuts it at A(0, 2 ) and A'(0, -2)x=2 is a line parallel to y-axis, cutting the x-axis at C(2, 0)The enclosed area of the curve between x=0 and x=2 and above x-axis =area OABCConsider, a vertical strip of length =y and width =dx Area of approximating rectangle =y dxThe approximating rectangle moves from x=0 to x=2 ⇒area OABC =∫02y dx⇒A=∫02y dx As, y>0 , y =y⇒A=∫026x+4 dx ⇒A=∫026x+412 dx⇒A=166x+4323202⇒A=2181632-432⇒A=21843-23⇒A=21864-8 =218×56 =569 sq. units∴Enclosed area =569 sq. units

Q9.

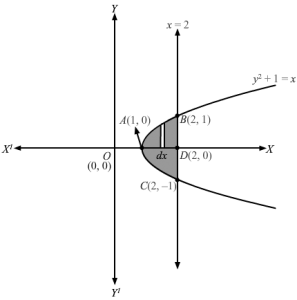
y2+1=x, x≤2 is a parabola with vertex (1, 0) and symmetrical about +ve side of x-axis x=2 is a line parallel to y-axis and cutting x-axis at (2, 0)Consider, a vertical section of height= y and width =dx in the first quadrant⇒ area of corresponding rectangle = y dxSince, the corresponding rectangle is moving from x=1 to x=2 and the curve being symmetrical∴A=area ABCA=2×area ABDA⇒A=2∫12y dx ⇒A=2∫12y dx y=y as y>0⇒A=2∫12x-1 dx y2+1=x ⇒y=x-1 ⇒A=2x-1323212 ⇒A=43132-0⇒A=43 sq. units∴Enclosed area=43 sq. units

Q10.

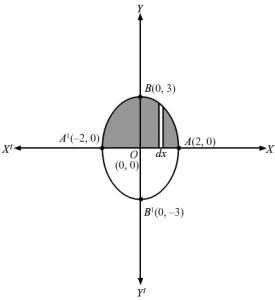
Since in the given equation x24+y29 =1, all the powers of both x and y are even, the curve is symmetrical about both the axis .∴Area encloed by the curve and above x axis = area A’BA =2×area enclosed by ellipse and x-axis in first quadrant(2, 0 ), (-2, 0) are the points of intersection of curve and x-axis(0, 3), (0, -3) are the points of intersection of curve and y-axisSlicing the area in the first quadrant into vertical stripes of height =y and width =dx∴Area of approximating rectangle =y dxApproximating rectangle can move between x=0 and x=2 A=Area of enclosed curve above x-axis =2∫02y dx⇒A=2∫02y dx⇒A=2∫02324-x2 dx⇒A=3∫024-x2 dx⇒A=312x 4-x2 +12 4 sin-1×02=30+12×4 sin-11=3×12×4×π2= 3π sq. units∴Area of enclosed region above x-axis = 3π sq. units

Q11.

We have,9×2+4y2=36 …..1⇒4y2=36-9×2⇒y2=944-x2⇒y=324-x2 …..2From 1 we get⇒x24+y29 =1Since in the given equation x24+y29 =1, all the powers of both x and y are even, the curve is symmetrical about both the axes.∴Area enclosed by the curve and above x axis = 4×area enclosed by ellipse and x-axis in first quadrant(2, 0 ), (-2, 0) are the points of intersection of curve and x-axis(0, 3), (0, -3) are the points of intersection of curve and y-axisSlicing the area in the first quadrant into vertical stripes of height =y and width =dx∴Area of approximating rectangle =y dxApproximating rectangle can move between x=0 and x=2A=Area of enclosed curve=4∫02y dx⇒A=4∫02324-x2dx From 2=4×32∫024-x2dx=6∫0222-x2dx=6×222-x2+1222sin-1×202=60+124sin-11=612×4π2⇒A=6π sq units

Q12.

We have,y=21-x2⇒y2=1-x2⇒y24=1-x2⇒x2+y24=1⇒x21+y24=1Since in the given equation x21+y24 =1, all the powers of both x and y are even, the curve is symmetrical about both the axes .∴Required area=area enclosed by ellipse and x-axis in first quadrant(1, 0 ), (-1, 0) are the points of intersection of curve and x-axis(0, 2), (0, -2) are the points of intersection of curve and y-axisSlicing the area in the first quadrant into vertical stripes of height =y and width =dx∴Area of approximating rectangle =y dxApproximating rectangle can move between x=0 and x=1 A=Area of enclosed curve above x-axis =∫01y dx⇒A=∫0121-x2 dx=2∫011-x2 dx=212×1-x2+12sin-1×01=212sin-11=212π2-0⇒A=π2 sq.units

Q13.

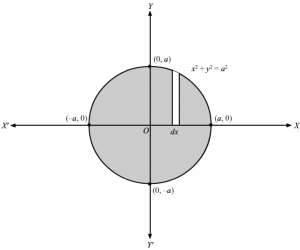
We have,y=a2-x2⇒y2=a2-x2⇒x2+y2=a2Since in the given equation x2+y2=a2, all the powers of both x and y are even, the curve is symmetrical about both the axis .∴Required area = area enclosed by circle in first quadrant(a, 0 ), (-a, 0) are the points of intersection of curve and x-axis(0, a), (0, -a) are the points of intersection of curve and y-axisSlicing the area in the first quadrant into vertical stripes of height =y and width =dx∴Area of approximating rectangle =y dxApproximating rectangle can move between x=0 and x=aA=Area of enclosed curve in first quadrant =∫0ay dx⇒A=∫0aa2-x2 dx=12xa2-x2+12a2sin-1xa0a=12a2sin-11=12a2π2 =a2π4 sq units

Q14.

We have,
Straight line 2y = 5x + 7 intersect x-axis and y-axis at ( −1.4, 0) and (0, 3.5) respectively.
Also x = 2 and x = 8 are straight lines as shown in the figure.
The shaded region is our required region whose area has to be found.
When we slice the shaded region into vertical strips, we find that each vertical strip has its lower end on x-axis and upper end on the line
2y = 5x + 7
So, approximating rectangle shown in figure has length = y and width = dx and area = y dx.
The approximating rectangle can move from x = 2 to x = 8.
So, required is given by,
A=∫28y dx=∫285x+72 dx=12∫28(5x+7) dx=1252×2+7×28=1252×64+56-52×4-14=12×192=96 sq units

Q15.

Area of the circle x² + y² = a² will be the 4 times the area enclosed between x = 0 and x = a in the first quadrant which is shaded.
A=4∫0ay dx=4∫0aa2-x2 dx=412xa2-x2+12a2sin-1xa0a=40+12a2sin-11=412a2π2 ∵ sin-11=π2=a2π sq units

Q16.

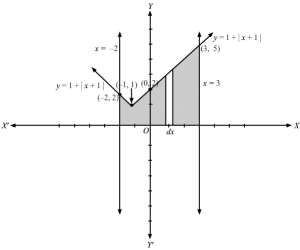
We have,
y = 1 + | x + 1 | intersect x = − 2 and at ( −2, 2) and x = 3 at (3, 5).
And y = 0 is the x-axis.
The shaded region is our required region whose area has to be found

y=1+x+1=1-x+1 x<-11+x+1 x≥1=-x x<-1x+2 x≥1
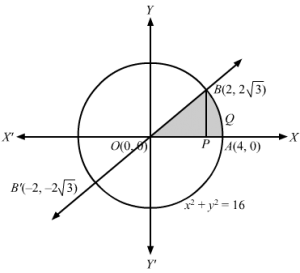
Let the required area be A. Since limits on x are given, we use horizontal strips to find the area:
A=∫-23ydx=∫-2-1ydx+∫-13ydx=∫-2-1-x dx+∫-13x+2dx=-x22-2-1+x22+2x-13=-12-42+92+6-12+2=32+8+82=32+8+4=272 sq. units

Q17.

Answer :

We have,
y = | x − 5 | intersect x = 0 and x = 1 at (0, 5) and (1, 4)
Now,
y=x-5=-x-5 For all x∈0, 1
Integration represents the area enclosed by the graph from x = 0 to x = 1
A=∫01ydx=∫01x-5 dx=∫01-x-5 dx=-∫01x-5 dx=-x22-5×01=-12-5-0-0=–92=92 sq. units

Q18.

We have,
y = | x + 3 | intersect x = 0 and x = −6 at (0, 3) and (−6, 3)
Now,
y=x+3=x+3 For all x>-3-x+3 For all x<-3

Integral represents the area enclosed between x = −6 and x = 0
∴A=∫-60y dx=∫-6-3y dx+∫-30y dx=∫-6-3-x+3 dx+∫-30x+3 dx=-x22+3x-6-3+x22+3x-30=-92-9-362+18+0+0-92+9=-92+9+362-18-92+9=9 sq.

units

Q19.

Answer :

We have,
y = | x + 1 | intersect x = −4 and x = 2 at (−4, 3) and (2, 3) respectively.
Now,
y=x+1=x+1 For all x>-1-x+1 For all x<-1

Integral represents the area enclosed between x = −4 and x = 2
A=∫-42ydx=∫-4-1ydx+∫-12ydx=∫-4-1-x+1dx+∫-12x+1dx=-x22+x-4-1+x22+x-12=-12-1-162+4+42+2-12+1=-3-152+5-12=-3+152+5-12=9 sq. units

Q20.

Answer :

We have,
xy-3x-2y-10=0⇒xy-2y=3x+10⇒yx-2=3x+10⇒y=3x+10x-2
Let A represent the required area:
⇒A=∫34ydx=∫343x+10x-2dx=∫343x-6+16x-2dx=∫343+16x-2dx=3x+16 log x-234=12+16 log 2 -9 -16 log 1=3+16 log 2 sq. units

Q21.

x	0	π6	π2	5π6	π
sin x	0	12	1	12	0
y=π2+2sin2x	1.57	2.07	3.57	2.07	1.57

y=π 2+2 sin2 x is an arc cutting y-axis at (1.57, 0 ) and x=π at π, 1.57x=π is a line parallel to y-axis Consider, a vertical strip of length =y and width =dx in the first quadrant∴Area of the approximating rectangle =y dx The approximating rectangle moves from x=0 to x=π ⇒Area of the shaded region =∫0πy dx ⇒A=∫0πy dx ⇒A=∫0ππ 2+2 sin2x dx⇒A=∫0ππ 2+21-cos 2×2 dx⇒A=π 2∫0πdx +∫0π1-cos 2x dx⇒A=π 2×0π +x-sin 2×20π⇒A=π 2π + π -sin 2π 2-0⇒A=π π 2+1⇒A=π π+2 2⇒A=π2 π+2 sq. units∴Area of curve bound by x=0 and x=π is π2 π+2 sq. units

Q22.

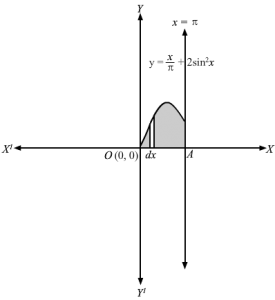
The table for different values of x and y is

x	π6	π2	5π6	π
sinx	12	1	12	0
y=xπ+2sin2 x	23	52	43	1

y=xπ+2 sin2 x , is an arc cutting y-axis at O(0, 0) and cutting x=π at π, 1 Consider a vertical strip of length = y and width = dx in the first quadrant∴ Area of approximating rectangle = y dxThe approximating rectangle moves from x=0 to x=π⇒Area of the shaded area =∫0πy dx⇒A=∫0πy dx As, y>0 ⇒ y =y⇒A=∫0πxπ+2 sin2 x dx⇒A=1π∫0πx dx +2 ∫0πsin2 x dx⇒A=1πx220π+2×2-12sin x cos x 0π⇒A=π22π+22π-12sin π cos π -0 ⇒A=π2+π⇒A=3π2 sq. units ∴Area of the curve enclosed between x=0 and x=π is 3π2 sq. units

Q23.

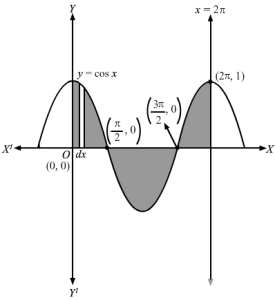
The shaded region is the required area bound by the curve y=cos x , x axis and x=0 , x=2πConsider a vertical strip of length= y and width= dx in the first quadrant Area of the approximating rectangle = y dxThe approximating rectangle moves from x=0 to x=2πNow ,0≤x≤π2and 3π2≤x≤2π , y>0⇒y =yπ2≤x≤3π2, y<0⇒y =-y⇒Area of the shaded region =∫02π y dx⇒A=∫0π2 y dx +∫π23π2 y dx +∫3π22π y dx⇒A=∫0π2 y dx +∫π23π2-y dx +∫3π22π y dx⇒A=∫0π2 cos x dx +∫π23π2-cos x dx +∫3π22πcos x dx⇒A=sin x0π2+-sin xπ23π2+-sin x3π22π⇒A=1+1+1+0–1⇒A=4 sq. units Area bound by the curve y=cos x, x-axis and x=0, x=2π=4 sq. units

Q24.

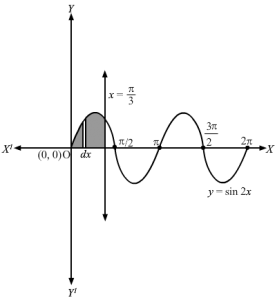
The shaded area A1 is the required area bound by the curve y=sin x and x=0, x=π3The shaded area A2 is the required area bound by the curve y=sin 2x and x=0, x=π3∴ A1 =∫0π3y dx⇒A1=∫0π3y dx As, y>0 , y=y⇒A1=∫0π3sin x dx⇒A1=-cos x0π3 ⇒A1=-cos π3+cos 0⇒A1=-12+1=12 … 1And, A2=∫0π3y dx⇒A2=∫0π3y dx As, y>0 , y=y⇒A2=∫0π3sin 2x dx⇒A2=∫0π32 sin x cos x dx⇒A2=2-14cos 2×0π3⇒A2=12-cos 2π3+cos 0⇒A2=121+12 =12×32 … 2From 1 and 2A1A2=12 12×32=23 Thus, the area of curve y=sin x and y=sin 2x for x=0 and x=π3 are in the ratio 2 : 3

Page 21.15 Ex.21.1

Q25.

Consider the value of y for different values of x

x	0	π4	π3	π2	2π3	5π6	π
y=cos2 x	1	0.5	0.25	0	0.25	0.75	1
y =sin2x	0	0.5	0.75	1	0.75	0.25	0

Let A₁ be the area of curve y=cos2x between x=0 and x=π
Let A₂ be the area of curve y=sin2 x between x=0 and x=π

Consider, a vertical strip of length =y and width =dx in the shaded region of both the curves

The area of approximating rectangle =y dx

The approximating rectangle moves from x=0 to x=πA1=∫0πy dx⇒A1=∫0πy dx 0≤x≤π , y>0 ⇒y=y⇒A1=∫0πcos2 x dx⇒A1=∫0π1+cos 2x dx cos2 x=1+cos 2x ⇒A1=12x+sin 2×20π⇒A1=12π+sin 2π2-0⇒A1=π2 Sq. unitsAlso,A2=∫0πy dx⇒A2=∫0πy dx 0≤x≤π , y>0 ⇒y=y⇒A2=∫0πsin2 x dx⇒A2=x2-14sin 2×20π⇒A2=π2-14sin 2π2⇒A2=π2 sq. units∴Area of curves y=cos2 x and area of curve y=sin2 x are both equal to π2sq. units

Q26.

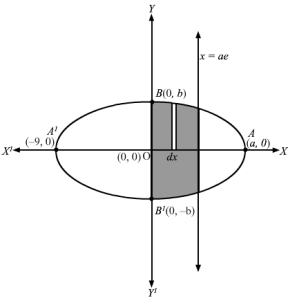
x2a2+y2b2=1 represents a parabola , symmetrical about both the axis .It cuts x axis at Aa, 0 and A’-a, 0It cuts y axis at B0, b and B’0, -bx=ae is a line parallel to y axis Consider a vertical strip of length =y and width=dx ,in the first quadrantArea of approximating rectangle in first quadrant = y dxApproximating rectangle moves from x=0 to x=aeArea of the shaded region =2 area in the first quadrant ⇒A=2∫0aey dx⇒A=2∫0aey dx As, y>0 , y=y⇒A=2∫0aebaa2-x2 dx x2a2+y2b2=1 ⇒y=baa2-x2 ⇒A=2ba∫0aea2-x2 dx ⇒A=2ba12xa2-x2 +12a2sin-1xa0ae⇒A=2ba12aea2-a2e2 +12a2sin-1aea-0⇒A=baa2e1-e2 +12a2sin-1e⇒A=baa2e1-e2 +12sin-1e⇒A=abe1-e2 +12sin-1e sq. units∴Required area of the ellipse bound by x=0 and x=ae is= abe1-e2 +12sin-1e sq. units

Page 21.21 Ex.21.2

Q1.

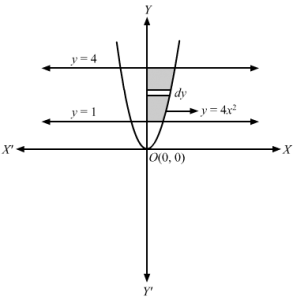
y=4×2 represents a parabola , openeing upwards, symmetrical about +ve y-axis and having vertex at O(0, 0)y=1 is a line parallel to x-axis , cutting parabola at -12 , 1 and 12, 1y=4 is a line parallel to x axis , cutting parabola at -1, 1 and 1, 1x=0 is the y-axis Consider a horizontal strip of length= x and width=dy in the first quadrantArea of approximating rectangle =x dyApproximating rectangle moves from y=1 to y=4 Area of the curve in the first quadrant enclosed by y=1 and y=4 is the required area of the shaded region ∴Area of the shaded region =∫04x dy⇒A=∫14x dy As, x>0, x =x⇒A=∫14y4 dy ⇒A= 12∫14y dy ⇒A=12y323214⇒A=12×23432-132⇒A=138-1⇒A=73 sq. units∴The area enclosed by parabola in the first quadrant and y=1, y=4 is 73 sq. units

Q2.

x2=16 y is a parabola, with vertex at O0, 0 and symmetrical about +ve y-axis y=1 is line parallel to x-axis cutting the parabola at -4, 1 and 4, 1 y=4 is line parallel to x axis cutting the parabola at -8, 1 and 8, 1 Consider a horizontal strip of length= x and width =dy∴ Area of approximating rectangle = x dy The approximating rectangle moves from y=1 to y=4 Area of the curve in the first quadrant enclosed by y=1 and y=4 is the shaded area∴Area of the shaded region =∫14x dy⇒A=∫14x dy As, x>0, x=x⇒A=∫1416 y dy⇒A=4∫14y dy⇒A=4y323214⇒A=83432-132⇒A=83×7=563 sq. units∴Area enclosed by parabola in the first quadrant and y=1 and y=4 is 563 sq. units

Page 21.22 Ex.21.2

Q3.

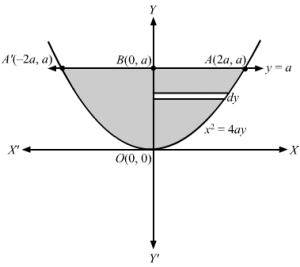
x2=4ay represents a parabola with vertex O(0, 0) opening upwards and symmetrical about y-axis. F(0, a ) is the focus of the parabola and y=a its latus rectumConsider a horizontal strip of length =x and width dy in the first quadrant ∴Area of approximating rectangle=x dyThe approximating rectangle moves from y=0 to y=a ⇒Area OAB =∫0ax dy⇒Area OAA’O=2×Area OAB ⇒A=2∫0ax dy =∫0ax dy As, x>0 ⇒x=x⇒A=2∫0a4ay dy⇒A=2×2a∫0ay dy⇒A=4a y32320a⇒A=4a 23a32-0⇒A=83a2 sq. units

Q4.

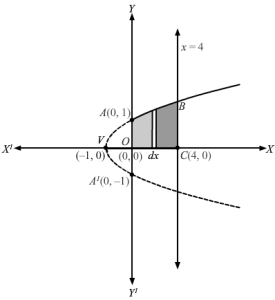
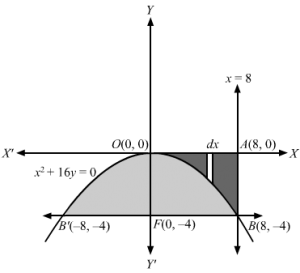
x2+16 y=0 ⇒x2 =-16 yComparing it with equation of parabola x2=4ay⇒a=-4Thus, x2+16 y=0 represents a parabola, opening downwards, with vertex at O(0, 0) and -ve y-axis being its axis of symmetry Focus of the parabola is F(0, -4)y=-4 is the latus rectum of the parabolaThe latus rectum cuts the parabola at B(8, -4) and B'(-8, -4)x=8 cuts the x-axis at A(8, 0)Area of the curve bound by latus rectum= Shaded area BOB’B= 2 Area OBF …1Consider a vertical strip of length= y and width=dx in shaded area OAB such that point P(x, y ) lies on the parabolaThe area of the approximating rectangle = y dxBut the approximating rectangle moves from x=0 to x=8∴Area of the shaded region OAB=∫08y dx ⇒A=∫08-x2 16 dx ∵ x2=-16 y⇒y=-x2 16 ⇒Area of the shaded region OAB=∫08 x2 16 dx =116×13×308=8×8×816×3=323 sq. units …2So, area of rectangle OABF = OA ×AB =8×4 =32 sq. units …3 From 2 and 3Area of OBF=Area of rectangle OABF -Area of the shaded region OAB=32 -323=643 sq. units ⇒Shaded area BOB’B= 2 Area OBF=2×643=1283 sq. units Thus, area of the curve x2+16 y =0 bound by its latus rectum =1283 sq. units

Page 21.47 Ex.21.3

Q1.

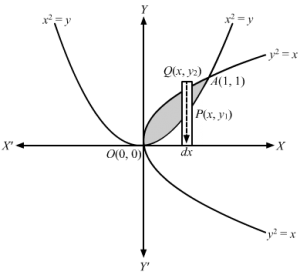
y2=x is a parabola, opening sideways, with vertex at O(0, 0) and +ve x-axis as axis of symmetry x2 =y is a parabola, opening upwards, with vertex at O(0, 0) and +ve y-axis as axis of symmetry Soving the above two equations,x2=y4=y ⇒y4-y =0 ⇒y=0 or y=1 . So, x=0 or x=1⇒O0, 0 and A(1, 1) are points of intersection of two curvesConsider a vertical strip of length = y2-y1 and width= dx ⇒Area of approximating rectangle =y2-y1 dx Approximating rectangle moves from x=0 to x=1⇒Area of the shaded region =∫01y2-y1 dx ⇒A=∫01 y2-y1 dx As, y2-y1>0 ⇒y2-y1=y1⇒A=∫01 x -x2 dx ⇒A=x3232-x3301⇒A=23×132-133 -0⇒A=23-13⇒A=13 sq. units Thus, area enclosed by the curves =13 sq. units

Q2.

3×2=16 y … 1 is a parabola with vertex at (0, 0) opening upwards and symmetrical about +ve y-axis 4y2=9x … 2 is a parabola with vertex at (0, 0) opening sideways and symmetrical about +ve x-axis Solving the equations 1 and 2, we get the points of intersection of the two parabolas O(0, 0) and A(4, 3 ) Consider a vertical strip of length= y2-y1 and width = dx such that P(x, y1) lies on 1 and Q(x, y2) lies on 2⇒area of approximating rectangle =y2-y1 dx Approximating rectangle moves from x=0 to x=4⇒Area of the shaded region =∫04y2-y1 dx =∫04y2-y1 dx As, y2-y1 =y2-y1 for y2-y1>0 ⇒A=∫0494x -316×2 dx ⇒A=32∫04x dx -316∫04×2 dx ⇒A=32×323204-316×3304⇒A=432-116×43⇒A=8-4=4 sq. units ∴Area bound by the two curves = 4 sq. units

Q3.

y=x … 1 is a parabola opening side ways, with vertex at O(0, 0) and +ve x-axis as axis of symmetry x=y …2 is a straight line passsing through O(0, 0) and at angle 45o with the x-axisSolving 1 and 2 y2=x=y ⇒y2=y ⇒y(y-1)=0 ⇒y=0 or y=1 and x=0 or x=1Thus, the line intersects the parabola at O(0, 0 ) and A(1, 1)Consider a approximating rectangle of length =y2-y1 and width= dx Area of approximating rectangle= y2 -y1 dxApproximating rectangle moves from x=0 to x=1 ∴Area of the shaded region=∫01 y2 -y1 dx =∫01 y2 -y1 dx As, y2 >y1, y2 -y1=y2-y1 ⇒A=∫01 x -x dx ⇒A=x3232-x2201⇒A=13232-122-0⇒A=23-12=16 sq. units ∴Area bound by the parabola and straight line = 16 sq. units

Q4.

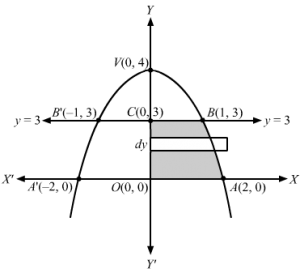
y=4-x2 is a parabola, with vertex (0, 4), opening downwars and having axis of symmetry as -ve y-axis y=0 is the x-axis, cutting the parabola at A(2, 0) and A'(-2, 0)y=3 is a line parallel to x-axis, cutting the parabola at B(1, 3 ) and B'(-1, 3) and y-axis at C(0, 3) Required area is the shaded area ABB’A =2 area ABCOConsider a horizontal strip of length= x2-x1 and width=dy in the shaded region Area of approximating rectangle= x2-x1 dyThe approximating rectangle moves from y=0 to y=3 ∴Area of shaded region = 2∫30×2-x1 dy ⇒A=2∫03×2-x1 dy As, x 2-x1 =x2-x1 , x2>x1 ⇒A=2∫034-y -0 dy⇒A=-24-y3232 03⇒A=-24-y3232 03⇒A=2 ×23432-132⇒A=43×7 ⇒A=283 sq. units∴Area bounded by the two parabolas =283 sq. units

Q5.

Let R=x, y : x2 a2+y2b2≤ 1≤xa+yb⇒R1=x, y : x2 a2+y2b2≤ 1and R2 =x, y : 1≤xa+ybThen, R =R1∩R2Consider x2 a2+y2b2=1. This represents an ellipse, symmetrical about both axis and cutting x-axis at A(a, 0) and A'(-a, 0) and y-axis at B(0, b), B'(0, -b)⇒ R1= x2 a2+y2b2≤ 1 represents the area inside the ellipse xa+yb=1 = represents a straight line cutting x-axis at A(a, 0) and y-axis at B(0, b)⇒R2=xa+yb≥1represents the area above the straight line ⇒R =R1∩R2 represents the smaller shaded area bounded by the line and the ellipse In the shaded region, consider a vertical strip with length=y2-y1 and width =dx, such that P(x, y2) lies on ellipse and Q(x, y1) lies on the straight line Area of approximating rectangle=y2 -y1 dx The approximating rectangle moves from x=0 to x=a∴Area of the shaded region =∫0ay2 -y1 dx =∫0ay2 -y1 dx As, y2>y1, y2 -y1= y2-y1 ⇒A= ∫0abaa2-x2 -baa-x dx⇒A=∫0abaa2-x2dx – ∫0abaa-x dx⇒A=bax2a2-x2+12a2 sin-1xa0 a -baax-x22⇒A=ba0+12a2 sin-11-a2-a22⇒A=ba12a2×π2-a22⇒A=ab2π2-1⇒A=ab4π-2 sq. units

Q6.

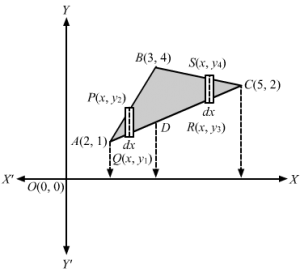
Consider the points A(2, 1), B(3, 4) and C(5, 2) We need to find area of shaded triangle ABCEquation of AB is y-1=4-33-2 x-2⇒3x-y-5=0 … 1Equation of BC isy-4=2-45-3 x-3⇒x=y-7=0 … 2Equation of CA is y-2=2-15-2 x-5⇒x-3y+2=0 … 3Area of ΔABC =Area of ΔABD+Area of ΔDBC In ΔABD, Consider point P(x, y2) on AB and Q(x, y1) on AD Thus, the area of approximating rectangle with length=y2-y1 and width=dx is y2-y1 dxThe approximating rectangle moves from x=2 to x=3∴ Area of ΔABD =∫23y2-y1 dx =∫23y2-y1 dx ⇒A=∫233x-5-x+13 dx⇒A=∫239x-15-x-13 dx ⇒A=∫238x-163 dx⇒A=138×22-16×23⇒A=134×32-16×3-4×22+16×2⇒A=1368-64⇒A=43 sq. units Similarly, for S(x, y4) on AB and R(x, y3) on DC Area of approximating rectangle of length y4-y3 and width dx= y4-y3 dxApproximating rectangle moves from x=3 to x=5∴Area BDC=∫35y4-y3 dx⇒A=∫357-x -x+13 dx⇒A=13∫3520-4x dx⇒A=1320 x-4×2235⇒A=13100-50-60-18⇒A=1350-42=83 sq. units ∴Area of ΔABC =Area of ΔABD +Area of ΔDBC=43+83=123 =4 sq. units

Q7.

Equation of line AB isy-1=5-10+1x–1⇒y=4x+5 Area under the line AB = area ABDO=∫-104x+5 dx=4×22+5x-10=0-2-5⇒Area ABDO=3 sq. units … 1Equation of line BC is y-5=2-53-0x-0⇒y=-x+5 Area under line BC =Area OBCP=∫03-x+5 dx=-x22+5×03=-92+15 -0⇒Area OBCP=212 sq. units … 2Equation of line CA isy-2=2-13–1x-3 ⇒4y =x+5∴Area under line AC =Area ACPA⇒A=∫-13x+54dx⇒A=14×22+5x-13⇒A=14322+5×3–122+5-1⇒A=1492+15-12+5⇒Area ACPA=244=6 sq. units … 3From 1, 2 and 3Area Δ ABC =Area ABDO+Area OBCP-Area ACPA⇒A=3+212-6⇒A=212-3 =21-62=152 sq. units ∴Area Δ ABC=152 sq. units

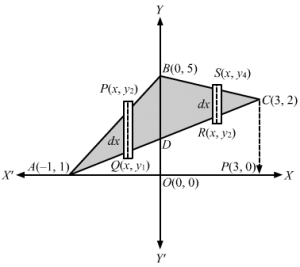
Q8.

Solving the given equations The point of intersection of the three lines are A(0, 1), B(4, 13) and C(4, 9). We need to find the area of ABCArea under line AB=area OABCL⇒Area OABCL=∫043x+1 dx Equation of BC is y=3x+1 and x moves from A, x=0 to B, x=4 =3×22+x04 =3422+4=24+4=28 sq. unitsArea under line BC =Area OACL⇒Area OACL=∫042x+1dx Equation of BC is y=2x+1 and x moves from A, x=0 to C, x=4 =2×22+x04=16+4=20 sq. units∴Area ΔABC = Area OABCL-Area OACL⇒Area ΔABC=28-20 =8 sq. units ∴Area of triangle formed by the three given lines=8 sq. units

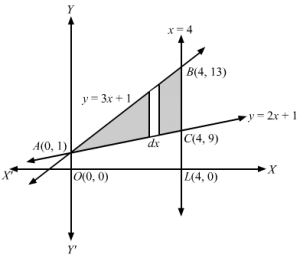
Q9.

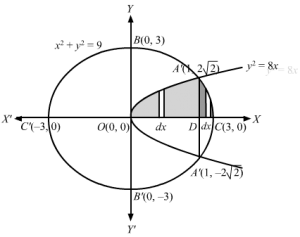
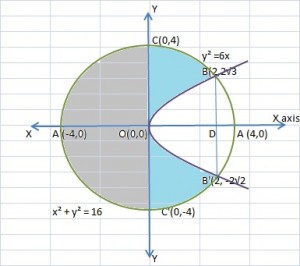
Let R=x, y: y2≤8x, x2+y2≤9R1=x, y: y2≤8xR2=x, y: x2+y2≤9Thus, R=R1∩R2 Now, y2=8x represents a parabola with vertex O(0, 0) and symmetrical about x-axis Thus, R1 such that y2≤8x is the area inside the parabola Also, x2+y2=9 represents with circle with centre O(0, 0) and radius 3 units. The circle cuts the x axis at C(3, 0) and C'(-3, 0 ) and Y-axis at B(0, 3) and B'(0, -3 )Thus, R2 such that x2+y2≤9 is the area inside the circle⇒R =R1∩R2 =Area OACA’O=2 shaded area OACO … 1The point of intersection between the two curves is obtained by solving the two equationsy2=8x and x2+y2=9 ⇒x2+8x=9 ⇒x2+8x -9 =0⇒x+9x-1=0⇒x=-9 or x=1Since, parabola is symmetric about +ve x-axis, x=1 is the correct solution ⇒y2=8 ⇒y=±22Thus, A1, 22 and A’ 1, -22 are the two points of intersectionArea OACO =area OADO +area DACD … 2Area OADO =∫018x dx Area bound by curve y2=8x between x=0 and x=1=22×323201⇒Area OADO=423 … 3∴Area DACD = area bound by x2+y2=9 between x=1 to x=3⇒A=∫139-x2 dx =12×9-x2+129 sin-1×313=0+92 sin-133 -129-12 -92 sin-113=92 sin-11 -128 -92 sin-113=92 π2-1222 -92 sin-113⇒Area DACD=9 π4-2 -92 sin-113 … 4From 1, 2, 3 and 4R=Area OACA’O =2423+9 π4-2 -92 sin-113 =2423-2 +9 π4-92 sin-113 ∴Area OACA’O =223 +9π4-92 sin-113 sq. units

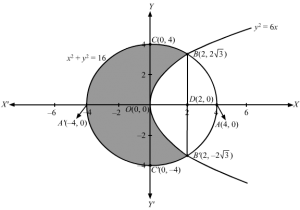
Q10.

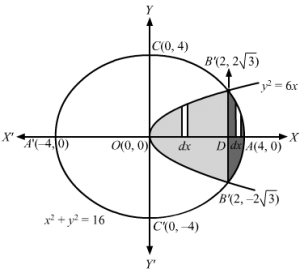
Points of intersection of the parabola and the circle is obtained by solving the simultaneous equations

x2+y2=16 and y2=6x⇒x2+6x=16 ⇒x2+6x-16 =0⇒x+8x-2=0⇒x=2 or x=-8 , which is not the possible solution. ∴ When x=2, y=±6×2 =±12=±23∴B2 ,23 and B’2 ,-23 are points of intersection of the parabola and circle. Now,Required area= areaOBAB’O =2areaOBAO =2areaOBDO+areaDBAD =2×∫026xdx +∫2416-x2 dx =2×6×323202+12×16-x2 +12×16 sin-1×424 =2× 6×23×232-0 +12416-42 +12×16 sin-144-12×216-22 -12×16 sin-124 =2 × 6×23×22+0+8 sin-11-12 -8 sin-112 =2×833+8×π2-23-8π6 =2 83-633+8π2-π6 =2233+82π6 =433+16π3

Q11.

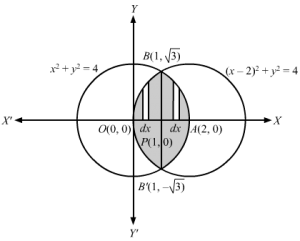
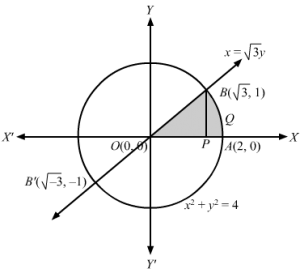
x2+ y2 = 4 …….(1) represents a circle with centre O(0,0) and radius 2
x-22+y2 = 4 ……(2) represents a circle with centre A(2 ,0) and radius 2

Points of intersection of two circles is given by solving the equations

x-22=x2⇒x2-4x+4 =x2⇒x=1 ∴y2=3 ⇒y =±3Now, B1,3 and B’1,-3 are two points of intersection of the two circlesWe need to find shaded area= 2×areaOBAO …1AreaOBAO=areaOBPO +areaPBAP =∫01y1dx+∫12y2dx ∵y1>0 ⇒y1=y1 and y2>0 ⇒y2=y2=∫01y1 dx+∫12y2dx=∫014-x-22 dx+∫124-x2 dx=12x-24-x-22 +12×4×sin-1x-2201+12×4-x2 +12×4×sin-1×212=-32+2sin-1-12 -0+2sin-1-1+0-123+2sin-11-sin-112=-32+2sin-1-12 -0-2sin-1-1+0-123+2sin-11-2sin-112=-3-4sin-112 +4sin-11=-3-4×π6 +4×π2=-3-2π3 +2π=4π3-3Now, From equation 1Shaded area= 2×areaOBAO=24π3-3=8π3-23 sq units

Q12.

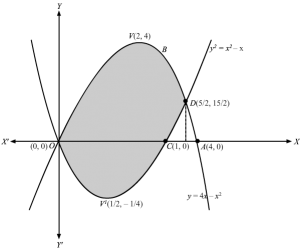
We have, y2=x and x+y=2
To find the intersecting points of the curves ,we solve both the equations.

y2+y-2=0⇒y+2y-1=0⇒y=-2 or y=1∴x=4 or 1Consider a horizantal strip of length x2-x1 and width dy where Px2,y lies on straight line and Qx1,y lies on the parabola.Area of approximating rectangle =x2-x1 dy , and it moves from y=-2 to y=1Required area = areaOADO =∫-21×2-x1 dy=∫-21×2-x1 dy ∵x2-x1=x2-x1 as x2>x1=∫-212-y-y2 dy=2y-y22-y33-21=2-12-13–4-2+83=2-12-13+6-83=92 sq units Area enclosed by the line and given parabola =92 sq units

Q13.

The given region is the intersection of
y2≤3x and 3×2+3y2≤16
Clearly ,y2 = 3x is a parabola with vertex at (0, 0) axis is along the x-axis opening in the positive direction.
Also 3×2 + 3y2 = 16 is a circle with centre at origin and has a radius 163.
Corresponding equations of the given inequations are
y2=3x …..1and3x2+3y2=16 …..2
Substituting the value of y2 from (1) into (2)
3×2+9x=16
⇒3×2+9x-16=0
⇒x=-9±81+1926
⇒x=-9±2736
By figure we see that the value of x will be non-negative.
∴x=-9+2736
Now assume that x-coordinate of the intersecting point, a=-9+2736
The Required area A = 2(Area of OACO + Area of CABC)
Approximating the area of OACO the length =y1 width = dx
Area of OACO =∫0ay1 dx
=∫0ay1 dx
=∫0a3xdx ∵y21=3x ⇒ y1=3x
=23 x323a0
=23a323
Therefore, Area of OACO =23a323
Similarly approximating the are of CABC the length =y2 and the width = dx
Area of CABC =∫a43y2 dx
=∫a43y2 dx
=∫a43163-x2 dx ∵3×2+3y22=16 ⇒y2=163-x2
=x2163-x2 +83sin-1x34a43
=423163-163+83sin-14343-a2163-a2-83sin-1a34

=-a2163-a2+83sin-11-83sin-1a34
Area of CABC =-a2163-a2+4π3-83sin-1a34
Thus the required area A = 2(Area of OACO + Area of CABC)
=223a323-a2163-a2+4π3-83sin-1a34
=4a323-a163-a2+8π3-163sin-1a34
Hence, the reguired area is,4a323-a163-a2+8π3-163sin-1a34 square units , where a=-9+2736

Q14.

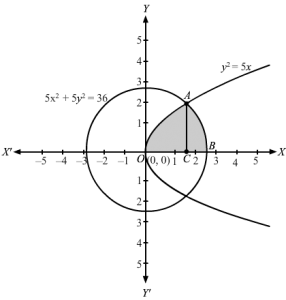
The given region is intersection of
y2≤5x and 5×2+5y2≤36
Clearly, y2≤5x is a parabola with vertex at origin and the axis is along the x-axis opening in the positive direction.Also 5×2+5y2≤36 is a circle with centre at the origin and has a radius 365 or 65.
Corresponding equations of given inequations are
y2=5x …..1 5×2+5y2=36 …..2
Substituting the value of y2 from (1) into (2), we get

5×2+25x=36
⇒5×2+25x-36=0
⇒x=-25±625+72010
⇒ x=-25±134510
From the figure we see that x-coordinate of intersecting point can not be negative.
∴x=-25+134510
Now assume that x-coordinate of intersecting point, a=-25+134510
The Required area,
A = 2(Area of OACO + Area of CABC)
Approximating the area of OACO the length =y1 and a width = dx=|y1=dx
Area of OACO=∫0ay1dx
=∫0ay1 dx
=∫0a5xdx ∵ y12=5x ⇒ y1=5x
= 52x323a0
Therefore, Area of OACO =25a323
Similarly approximating the area of CABC the length =y2 and the width = dx
Area of CABC=∫a65y2dx
=∫a65y2 dx
=∫a65365-x2dx
=x2365-x2 +185sin-1x56a65
=625365-365+185sin-11-a2365-a2-185sin-1a56
=0+185sin-11-a2365-a2-185sin-1a56
=185×π2-a2365-a2-185sin-1a56
Area of CABC =9π5-a2365-a2-185sin-1a56
Thus the Required area, A = 2(Area of OACO + Area of CABC)
A=2 25a323+ 9π5-a2365-a2-185sin-1a56
=45a323+18π5-a365-a2-365sin-1a56 , Where, a=-25+134510 .

Q15.

To find the points of intersection between two parabola let us substitute x=y24 in x2=4y.

y242=4y⇒y4-64y=0⇒yy3-64=0⇒y=0, 4
⇒x=0, 4

Therefore, the points of intersection are A(4, 4) and C0, 0.

Therefore, the area of the required region ABCD =∫04y1dx-∫04y2dx where y1=2x and y2=x24

Required Area
=∫042xdx-∫04x24dx=2×2×323-x31204=2×24323-4312-2×20323-0312

After simplifying we get,

=323-163=163 square units

Q16.

To find the point of intersection of the parabolas substitute y=x24b in y2=4ax we get

x416b2=4ax⇒x4-64ab2x=0⇒xx3-64ab2=0⇒x=0 and x=4ab23⇒y=0 and y=4a2b3

Therefore, the required area ABCD = ∫04ab23y1-y2dx where y1=2ax and y2=x24b.

Required area =
∫04ab23y1-y2dx=∫04ab232ax-x24bdx=4a3x32-x312b04ab23=4a34ab2332-4ab23312b-4a3032-0312a=16ab3square units

Q17.

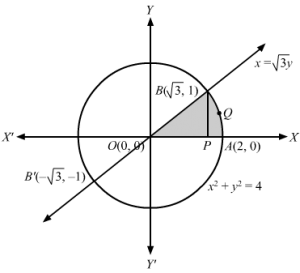
x2+y2 =4 represents a circle with centre O(0,0) and radius 2 , cutting x axis at A(2,0) and A'(-2,0)

x=3 y represents a straight line passing through O(0,0)

Solving the two equations we get

x2+y2 =4 and x=3 y ⇒3y2+y2=4⇒4y2 =4 ⇒y=±1⇒x =±3B3 , 1 and B’-3 , -1 are points of intersection of circle and straight lineShaded areaOBQAO= areaOBPO+area BAPB =13∫03 x dx+∫324-x2 dx =13×2203+12×4-x2+42sin-1×232 =32+0-32+2sin-1 1-sin-132 =32-32+2π2-π3 =π3 sq units Area bound by the circle and straight line above x axis =π3 sq units

Q18.

The given curves are
y=x-1 …..1
y=-x-1+1 …..2
Clearly y=x-1 is cutting the x-axis at (1, 0) and the y-axis at (0, 1) respectively.
Also y=-x-1+1 is cutting both the axes at (0, 0) and x-axis at (2, 0).
We have,
y=x-1y=x-1 x≥11-x x<1Andy=-x-1+1y=2-x x≥1 x x<1Solving both the equations for x<1y=1-x and y=x,We get x=12 and y=12And solving both the equations for x≥1y=x-1 and y=2-x,We get x=32 and y=12
Thus the intersecting points are 12, 12 and 32, 12.
The required area A = ( Area of ABFA + Area of BCFB)
Now approximating the area of ABFA the length = y1 and width = dx
Area of ABFA
=∫121x-1-xdx=∫1212x-1dx=x2-x121=14
Similarly approximating the area of BCFB the length =y2 and width= dx
Area of BCFB
=∫1322-x-x-1 dx=∫1323-2x dx=3x-x2132=14
Thus the required area A =( Area of ABFA + Area of BCFB)
=14+14=12
Hence the required area is 12 square units.

Q19.

Points of intersection of the parabola and the circle is obtained by solving the simultaneous equations

x2+y2=16a2 and y2=6ax⇒x2+6ax=16a2 ⇒x2+6ax-16a2=0⇒x+8ax-2a=0⇒x=2a or x=-8a , x=-8a is not the possible solution. ∴ When x=2a, y=±6a×2a =±12a=±23a∴B2a ,23a and B’2a ,-23a are points of intersection of the parabola and circle. Now, Required area= areaOBAB’O =2×areaOBAO =2areaOBDO+areaDBAD =2×∫02a6axdx +∫2a4a16a2-x2 dx =2×6ax323202a+12x16a2-x2 +12×16a2 sin-1x4a2a4a =2× 6a×23×2a32-0 +12×4a16a2-4a2 +12×16a2 sin-14a4a-12×2a16a2-2a2 -12×16a2 sin-12a4a =2 × 6a×23×2a2a+0+8a2sin-11-23a2 -8asin-112 =2×8a233+8a2×π2-23a2-8a2π6 =2 83-633a2+8π2-π6a2 =2233a2+8a22π6 =433a2+16π3a2 =4a234π+3

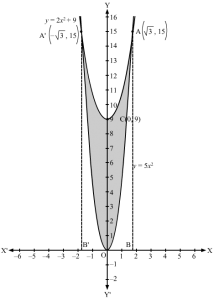
Q20.

The given equations are x2+y2=8x ⋯1 and y2=4x ⋯2
Clearly the equation x2+y2=8x is a circle with centre 4,0 and has a radius 4.Also y2=4x is a parabola with vertex at origin and the axis along the x-axis opening in the positive direction .
To find the intersecting points of the curves ,we solve both the equation.(2
∴ x2+4x=8x
⇒ x2-4x=0
⇒xx-4=0
⇒x=0 and x=4
When x=0, y=0
When x=4, y=±4

To approximate the area of the shaded region the length =y2-y1 and the width = dx
A=∫04y2-y1dx
=∫04y2-y1dx ∵y2>y1 ∴y2-y1= y2-y1
=∫0416-x-42 – 4xdx ∴y2=16-x-42 and y1=2x

=∫0416-x-42dx -∫044xdx
=x-4216-x-42+ 162sin-1x-4440-4×32340
=0+0-0-8sin-1-44-43×432
=8π2-323=4π-323
Hence the required area is 4π-323 square units.

Q21.

y=5×2 represents a parabola with vertex at O0,0 and opening upwards , symmetrical about +ve y axis y= 2×2+9 represents the wider parabola , with vertex at C0,9 To find point of intersection , solve the two equations 5×2=2×2+9 ⇒3×2=9⇒x=±3⇒y=15Thus A 3,15 and A’-3,15 are points of intersection of the two parabolas.Shaded area A’OA=2×areaOCAOConsider a vertical stip of length= y2- y1 and width=dx Area of approximating rectangle =y2- y1dx The approximating rectangle moves from x=0 to x=3∴AreaOCAO =∫03y2- y1dx =∫03y2- y1dx ∵y2- y1 =y2- y1 as y2>y1=∫032×2+9-5x2dx =∫039-3x2dx=9x-3×3303=93-33=63 sq units∴Shaded area B’A’AB=2 area OCAO =2×63 =123 sq unitsThus area enclosed by two parabolas =123 sq units

Q22.

We have, two parabolas y = 2x² and y = x² + 4

To find point of intersection , solve the two equations 2×2=x2+4⇒x2=4⇒x=±2∴y=4Thus A (2,4) and A'(-2 ,4 ) are points of intersection of the two parabolasShaded area =2×areaOCAOConsider a vertical stip of length y2- y1 and width dx Area of approximating rectangle=y2- y1 dx The approximating rectangle moves from x=0 to x=2AreaOCAO =∫02y2- y1dx =∫02y2- y1dx ∵y2- y1 =y2- y1 as y2>y1=∫02×2+4-2x2dx=∫024-x2dx=4x-x3302=8-82=163 sq unitsShaded area =2×areaOCAO =2×163 =323 sq units

Q23.

We have, y=2x and y=2x-x2
The two curves do not intersect each other
We need to find shaded area OABVO

x=2 is a line parallel to y axis , cutting y=2x at B 2,4We need to find shaded area OABVOConsider a vertical strip of length y2-y1 and width dx such that Px,y2 lies on y=2x and Qx,y1 lies on y=2x-x2 The area of approximating rectangle = y2-y1 dx The approximating rectangle moves from x=0 to x=2Thus area of shaded region =∫02 y2-y1 dx =∫02y2-y1 dx ∵y2>y1⇒y2-y1 = y2-y1=∫022x -2x-x2 dx =2xlog x-2×22+x3302=4log 2-4+83=3log 2-43 sq units Thus, Area bound by two curves = 3log 2-43 sq units

Q24.

3×2+5y=32 represents a downward opening parabola, symmetrical about negative x-axis

vertex of the parabola is D 0, 325 . It cuts the X axis at B323 ,0 and B’-323 ,0Also,y=x-2 ⇒y=x-2 , x≥22-x , x<2 y=x-2 , x≥2 represents a line , cutting the x axis at A2, 0 and the parabola at C 3, 1And y=2-x, x<2 represents a line, cutting the parabola at -2, 4Shaded area AEYCA =∫-2232-3×25-2-xdx +∫2332-3×25-x-2dx =∫-2332-3x25dx -∫-222-xdx +∫23x-2dx=1532x-x3-23-2x-x22-22-x22-2×23=1532×3-27+64-8-4-2+4+2-92-6-2+4=1596-35+64-8-92-4=1255-4-92=25-4-92=21-92=42-92=332 sq units

Q25.

x2 +y2 =25 represents a circle with centre O(0, 0 radius 5, Cutting the +ve x-axis at C5, 04y = 4-x2 ⇒4y =4-x2 -2≤x≤2×2 -4 x≥2⇒ 4y =4-x2 ,-2≤x≤2 represents an arc of the parabola opening down wards, vertex at V 0, 1, cutting the x axis at A 2,0 and A’-2, 0.and 4y =x2 -4 ,x≥2 represents an arc of the parabola opening up wards, vertex at 0,-1, cutting the x axis at A 2, 0 and A’-2, 0.Clearly A 2, 0 and A’-2, 0 are points of intersection of arcs of the two parabolas4y=x2 -4 cuts the circle at B4, 3 in the first quadrantThus area of shaded region = area of circle between x=0, x=4 – area of 4y =4-x2 between x=0 ,x=2 -area of 4y =x2 -4 between x=2, x=4=∫0425-x2dx-∫024-x2 4dx-∫24×2 -4 4dx=12×25-x2 +12×25sin-1×504 -4×4-x34×302-x34×3-4×424=12×4×3+12×25sin-145 -2-23-163-4-23+2=6+12×25sin-145-43-83=252sin-145 +2 sq units

Q26.

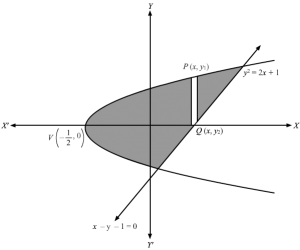
We have, y2 =2x+1 and x-y-1=0

To find the intersecting points of the curves ,we solve both the equations.

y2=21+y+1⇒y2-2-2y-1=0⇒y2-2y-3=0⇒y-3y+1=0⇒y=3 or y=-1∴x=4 or 0Consider a horizantal strip of length x2-x1 and width dy where Px2,y lies on straight line and Qx1,y lies on the parabola.Area of approximating rectangle =x2-x1 dy , and it moves from y=-1 to y=3Required area = areaOADO =∫-13×2-x1 dy=∫-13×2-x1 dy ∵x2-x1=x2-x1 as x2>x1=∫-131+y-12y2-1dy=∫-131+y-12y2+12dy=∫-1332+y-12y2dy=32y+y22-16y3-13=92+92-276–32+12+16=92+56=163 sq units Area enclosed by the line and given parabola =163 sq units

Q27.

We have, y = x − 1 and (y − 1)2 = 4 (x + 1)

∴x-1-12=4x+1⇒x-22=4x+1⇒x2+4-4x=4x+4⇒x2+4-4x-4x-4=0⇒x2-8x=0⇒x=0 or x=8∴y=-1 or 7Consider a horizantal strip of length x2-x1 and width dy where Px2,y lies on straight line and Qx1,y lies on the parabola.Area of approximating rectangle =x2-x1 dy , and it moves from y=-1 to y=7Required area = areaOADO =∫-17×2-x1 dy=∫-17×2-x1 dy ∵x2-x1=x2-x1 as x2>x1=∫-171+y-14y-12-4dy=∫-171+y-14y-12+1dy=∫-172+y-14y-12dy=2y+y22-112y-13-17=14+492-112×6×6×6–2+12+112×2×2×2=14+492-18–2+12+23=412+56=643 sq units Area enclosed by the line and given parabola =643 sq units

Q28.

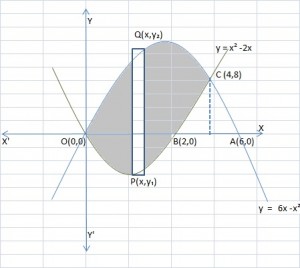
We have, y=6x -x2 and y=x2-2x

Solving the two equations, we get,∴x2-2x = 6x-x2 ⇒2×2 -8x =0⇒x = 0 or x = 4⇒y = 0 or y = 8 Consider a vertical strip of length=y2-y1 and width=dx in the shaded region Area of the shaded region =∫04y2-y1 dx=∫04y2-y1 dx ∵ y2-y1 ⇒y2-y1 as y2>y1 = ∫046x-x2 -x2-2x dx = ∫048x-2x2dx =8×22-2×3304=4×2-2×3304 =4×4×4-23×4×4×4=13×4×4×4 =643 sq units Area enclosed by the two parabolas =643 sq units

Q29.

Answer :

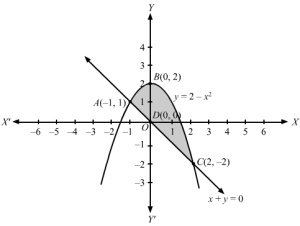
The graph of the parabola y=2-x2 and the line x+y=0 can be given as:

To find the points of intersection between the parabola and the line let us substitute x=-y in y=2-x2.

y=2-y2⇒y2+y-2=0⇒y-1y+2=0⇒y=1, -2
⇒x=-1, 2

Therefore, the points of intersection are A(-1, 1) and C2, -2.

The area of the required region ABCD =∫-12y1dx-∫-12y2dx where y1=2-x2 and y2=-x

Required Area
=∫-122-x2+xdx=2x-x33+x22-12=22-233+222-2-1–133+-122

After simplifying we get,

=92 square units

Q30.

We have, y=4x-x2 and y=x2-x
The points of intersection of two curves is obtained by solving the simultaneous equations

∴x2 -x=4x-x2⇒2×2 -5x =0 ⇒x=0 or x=52⇒y=0 or y=154⇒O0,0 and D 52 ,154 are points of intersection of two parabolas.In the shaded area CBDC , consider P(x,y2) on y =4x-x2 and Q(x,y1) on y=x2 -xAreaOBDCO = areaOBCO +areaCBDC=∫01y dx +∫152y2 -y1 dx=∫01y dx +∫152y2 -y1 dx ∵y>0 ⇒y =y and y2 -y1⇒y2-y1 as y2>y1 =∫014x-x2dx +∫1524x-x2-x2 -xdx=4×22-x3301+∫1525x-2x2dx=2×2 -x3301+5×22-2×33152=2-13+52522-23523 -52+23=53+5231-23 -116=53+52313-116=10-116+12524 =12124 sq units …1AreaOCV’O =∫01y dx =∫01-y dx ∵y<0 ⇒y =-y=∫01-x2 -xdx=∫01x-x2 dx=x22-x3 301=12-13=16 sq units …2From 1 and 2Shaded area=areaOBDCOand areaOCV’O =12124+16 =12524 sq units

Q31.

We have, y=x2+2 and y=x
We see that parabola and the line y=x do not intersect
x =1 is a line parallel to y axis

Point of intersection between parabola and x=1 is
Putting x=1 in y=x2+2, we get,y=1+2=3Point of intersection of two lines is given by Putting x=1 in y=x, we get,y=1 Consider a vetical strip of length y2-y1 and width=dx such that Px,y2 lies on parabola and Qx ,y1 lies on y=xShaded area=∫01y2-y1 dx=∫01y2-y1 dx ∵y2-y1 ⇒y2-y1as y2>y1 ,=∫01×2 +2-x dx=∫01×2 +2-xdx=x3 3-x2 2+2×01=13-12+2=2-3+126=116sq units Thus, area enclosed by parabola and given two lines =116 sq units

Q32.

x = y<sup>2</sup> is a parabola opening towards positive x-axis , having vertex at O (0,0) and symmetrical about x-axis
x = 3 − 2y<sup>2</sup> is a parabola opening negative x-axis, having vertex at A (3, 0) and symmetrical about x-axis, cutting y-axis at B and B’

Solving the two equations for the point of intersection of two parabolas

x =y2x=3-2y2⇒y2 =3-2y2 ⇒3y2 =3⇒y =±1y=1 ,⇒x=1 and y=-1 ⇒x=1⇒E1,1 and F1,-1are two points of intersection. The curve character changes at E and F .Draw EF parallel to y-axis.C(1, 0) is the point of intersection of EF ith x-axisSince both curves are symmetrical about x-axis ,Area of shaded region OEAFO = 2 Area OEAO =2Area OECO +area CEAC …..1Area OECO =∫o1y1 dx where Px, y1 is a point on x=y2 =∫o1y1 dx as y1 >0=∫o1x dx=x323201 =23 sq units …..2area CEAC =∫13y2 dx where Qx, y2 is a point on x=3-2y2 =∫13y2 dx as y2 >0 =∫133-x2dx=12∫133-x dx=12-3-x323213=12×230+232=2×222×3=43 sq. units …..3 From 1, 2 and 3, we get Therefore, area of Shaded region OEAFO =223 +43 =2×2 =4 sq units

Q33.

We have, y=4x-x2 and y=x2-x
The points of intersection of two curves is obtained by solving the simultaneous equations

∴x2 -x=4x-x2⇒2×2 -5x =0 ⇒x=0 or x=52⇒y=0 or y=154⇒O0,0 and D 52 ,154 are points of intersection of two parabolas.In the shaded area CBDC , consider P(x,y2) on y =4x-x2 and Q(x,y1) on y=x2 -xWe need to find ratio of areaOBDCOand areaOCV’OAreaOBDCO = areaOBCO +areaCBDC=∫01y dx +∫152y2 -y1 dx=∫01y dx +∫152y2 -y1 dx ∵y>0 ⇒y =y and y2 -y1⇒y2-y1 as y2>y1 =∫014x-x2dx +∫1524x-x2-x2 -xdx=4×22-x3301+∫1525x-2x2dx=2×2 -x3301+5×22-2×33152=2-13+52522-23523 -52+23=53+5231-23 -116=53+52313-116=10-116+12524 =12124 sq units …1AreaOCV’O =∫01y dx =∫01-y dx ∵y<0 ⇒y =-y=∫01-x2 -xdx=∫01x-x2 dx=x22-x3 301=12-13=16 sq units …2From 1 and 2 Ratio=AreaOBDCOAreaOCV’O=1212416=1214=121: 4 ≤

Page 21.49 Ex.21.3

Q34.

We have,y=x-1⇒y=x-1 for x≥11-x for x<1
y = x − 1 is a straight line passing through A(1, 0)
y = 1 − x is straight line passing through A(1, 0) and cutting y-axis at B(0, 1)

y=3-x⇒y=3-x for x≥o3–x =3+x for x<0

y = 3 − x is straight line passing through C(0, 3) and D(3, 0)
y = 3 + x is a straight line passing through C(0, 3) and D'(−3, 0)
The point of intersection is obtained by solving the simultaneous equations
y=x-1and y=3-xWe get⇒x-1=3-x⇒2x-4 =0⇒x=2⇒y=2-1=1Thus P2, 1 is point of intersection of y=x-1 and y=3-xPoint of intersection for y=1-xy=3+x⇒1-x=3+x⇒2x=-2⇒x=-1⇒y=1–1 =2 Thus Q-1, 2 is point of intersection of y=1-x and y=3+xSince the character of function changes at C0, 3 and A(1, 0) , draw AM perpendicular to x-axis Required area =Shaded areaQCPAQ= AreaQCB+AreaBCMAB+areaAMPA …..1 AreaQCB =∫-103+x -1-xdx=∫-102+2x dx=2x+x2-10= 0–2+1=1 sq unit …..2AreaBCMA =∫013-x-1-x dx=∫012 dx =2×01 = 2 sq unit …..3AreaAMPA =∫123-x-x-1 dx=∫124-2x dx=4x-x212 =8-4 -4-1=1 sq unit …..4From 1, 2, 3 and 4Shaded area =1+2+1 =4 sq units

Q35.

We have,y=x-1⇒y=x-1 x≥11-x x<1
y = x − 1 is a straight line originating from A(1, 0) and making an angle 45o with the x-axis
y = 1 − x is a straight line originating from A(1, 0) and making an angle 135o with the x-axis

y = x is a straight line parallel to x-axis and passing through B(0, 1)

The point of intersection of two lines with y = 1 is obtained by solving the simultaneous equations

y=1and y=x-1 ⇒1=x-1⇒x-2=0⇒x=2⇒C2, 1 is point of intersection of y=x-1 and y=1y=1 and y=1-x⇒1=1-x⇒x=0⇒B0, 1 is point of intersection of y=1-x and y=1Since y= x-1 changes character at A(1, 0) ,Consider point P (1,1) on BC such that PA is perpendicular to x-axis.Required shaded area ABCA = area ABPA+area PCAP=∫011-1-xdx +∫121-x-1dx=∫01x dx +∫122-x dx=x2201+2x-x2212=12+4-2-2+12=12+12=1 sq. unit

Q36.

We have, x2+y2 =32 and y=x

The point of intersection of the circle and parabola is obtained by solving the two equations

∴x2+x2=32⇒2×2=32 ⇒x2=16 ⇒x=±4 ∴y=±4 Thus C4, 4 and C’-4, -4 are points of intersection of the circle and straight line.Required shaded areaOCAPO = areaOCPO+areaPCAP=∫04y1dx+∫432y2dx=∫04y1 dx+∫432y2 dx ∵y1>0 ⇒y1=y1 and y2>0 ⇒y2=y2=∫04x dx+∫43232-x2 dx =x2204+12×32-x2+12×32 sin-1×32432= 8+8π -8-4π=4π sq units.

Q37.

Points of intersection of the parabola and the circle is obtained by solving the simultaneous equations

x2+y2=16 and y2=6x⇒x2+6x=16 ⇒x2+6x-16 =0⇒x+8x-2=0⇒x=2 or x=-8 , which is not the possible solution. ∴ When x=2, y=±6×2 =±12=±23∴B2 ,23 and B’2 ,-23 are points of intersection of the parabola and circle. Required area = AreaOB’C’A’CBO= area of circle -areaOBAB’O Area of circle with radius 4 =π×42=16π Now, Area OBAB’O =2areaOBAO =2areaOBDO+areaDBAD =2×∫026xdx +∫2416-x2 dx =2×6×323202+12×16-x2 +12×16 sin-1xa24 =2× 6×23×232-0 +12416-42 +12×16 sin-144-12×216-22 -12×16 sin-124 =2 × 6×23×22+0+8 sin-11-12 -8 sin-112 =2×833+8×π2-23-8π6 =2 83-633+8π2-π6 =2233+82π6 =433+16π3Shaded area =16π-433+16π3=48π-16π3- 433=32π3- 433=438π-3 sq units

Q38.

The points of intersection C and D are obtained by solving the two equations

∴x2=x+2⇒x2-x-2=0⇒x-2x+1=0⇒x=2 or x=-1⇒y=22=4 or y=-12=1Thus C(2,4 and D-1,1 are the points of intesection of two curvesConsider a vertical steip of length y2-y1 and width dx where Px,y2 lies on straight line and Qx,y1 lies on the parabola.Area of approximating rectangle =y2-y1 dx , and it moves from x=-1 to x=2Required area = areaODBCO =∫-12y2-y1 dx=∫-12y2-y1 dx ∵y2-y1=y2-y1 as y2>y1=∫-12x+2-x2 dx=∫-12x+2-x2 dx=x22+2x-x33-12=42+4-83-12+2-13=92 sq units Area enclosed by the line and given parabola =92 sq units

Q39.

R=x,y:0≤y≤x2+3 , 0≤y≤2x+3 , 0≤x≤3R1=x,y :0≤y≤x2+3 R2=x,y : , 0≤y≤2x+3 R3=x,y : 0≤x≤3⇒ R=R1∩R2∩R3

y = x2 + 3 is a upward opening parabola with vertex A(0, 3).
Thus R1 is the region above x-axis and below the parabola
y = 2x + 3 is a straight line passing through A(0, 3) and cuts y-axis on (−3/2, 0).
Hence R2 is the region above x-axis and below the line
x = 3 is a straight line parallel to y-axis, cutting x-axis at E(3, 0).
Hence R3 is the region above x-axis and to the left of the line x = 3.
Point of intersection of the parabola and y = 2x + 3 is given by solving the two equations
y=x2+3y=2x+3⇒x2+3=2x+3⇒x2-2x=0⇒xx-2=0⇒x=0 or x=2⇒y=3 or y=7⇒A0, 3 and B2, 7 are points of intersectionAlso ,x=3 cuts the parabola at C3, 12 and x=3 cuts y=2x+3 at D3, 9 We require thearea of shaded region. Total shaded area =∫02×2+3dx +∫232x+3 dx=x33+3×02+2×22+3×23=x33+3×02+x2+3×23=83+6+9+9-4-6=83+6+8=8+423=503 sq. units

Q40.

y=1-x2 ⇒y2 =1-x2⇒x2+y2 =1
Hence, y=1-x2 represents the upper half of the circle x2 + y2 = 1 a circle with centre O(0, 0) and radius 1 unit.
y = x represents equation of a straight line passing through O(0, 0)
Point of intersection is obtained by solving two equations

y=xy=1-x2⇒x=1-x2⇒x2=1-x2⇒2×2=1 ⇒x=±12 ⇒y=±12D12,12 and D’-12,-12 are two points of intersection between the circle and the straight lineAnd D12, 12 is the intersection point of y=1-x2 and y=x.Required area=Shaded area ODAEO =Area ODEO + area EDAE …..1Now, area ODEO =∫012x dx=x22012 =12122=14 sq units …..2Area EDAE =∫1211-x2 dx=12×1-x2+×12×sin-1×1121=0+12sin-11 -12×12×1-122 -12sin-112=12×π2-14-12×π4 using, sin-11=π2 and sin-112=π4=π4-π8-14=π8-14 sq units …..3From 1, 2 and 3, we getAreaODAEO =14+π8-14 =π8 sq. units

Q41.

We have,y=4x+5 …..1y=5-x …..24y=x+5 …..3
All the three equations represent equations of straight lines
The points of intersection is obtained by solving simultaneous equations
From 1 and 24x+5=5-x⇒5x=0⇒x=0 ⇒y=5 Thus A0, 5 is the point of intersection of 1 and 2From 2 and 345-x=x+5⇒5x=15⇒x=3⇒y=2Thus B3, 2 is the point of intersection of 2 and 3From 1 and 344x+5=x+5⇒15x=-15⇒x=-1⇒y=1Thus C-1, 1 is the point of intersection of 1 and 3Area ABC =areaABP +area PAB=∫-104x+5-x+54 dx +∫035-x-x+54 dx=∫-10154x+154 dx +∫03154-54x dx=154×22+x-10 +543x-x2203=154-12+1 +549-92=158+54×92=158+458 =608=152 sq. units

Q42.

Let the two curves be named as y1 and y2 where
y1:x-32+y2=9 …..1y2:x2+y2=9 …..2
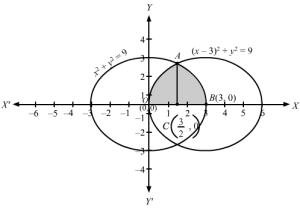
The curve x2 + y2 = 9 represents a circle with centre (0, 0) and the radius is 3.
The curve (x − 3)2 + y2 = 9 represents a circle with centre (3, 0) and has a radius 3.
To find the intersection points of two curves equate them.
On solving (1) and (2) we get
x=32 and y=±332
Therefore, intersection points are 32, 332 and 32, -332 .
Now, the required area(OABO) =2[area(OACO) +area(CABC)]
Here,
AreaOACO=∫032Y1dx
=∫0329-x-32dx
And
AreaCABC=∫323Y2dx
=∫3239-x2dx
Thus the required area is given by,
A = 2[area(OACO) +area(CABC)]
2∫0329-x-32 dx + ∫3239-x2dx
=2x-329-x-32+92sin-1x-33032+2×29-x2+92sin-1×3332
=232-329-33-32 +92sin-132-33-0-329-0-32-92sin-10-33+2329-32+92sin-133-349-94-92sin-1323

=2-938-9π12+9π4+29π4-938-9π12

=-1838-18π12+18π4+18π4-1838-18π12

=-3638-36π12+36π4

=-932-3π+9π
=6π-932
Hence the required area is 6π-932 square units.

Q43.

Let R=x, y: x2+y2≤4 ,x+y≥2R1=x, y: x2+y2≤4R2=x, y: x+y≥2∴R=R1∩R2
The region R1 represents interior of the circle x2 + y2 = 4 with centre (0, 0) and has a radius 2.
The region R2 lies above the line x + y =2
The line x + y =2 and circle x2 + y2 = 4 intersect each other at (2, 0) and (0, 2).
Here, the length of the shaded region is given by y2-y1 where y2 is y for the circle x2 + y2 = 4 and y1 is y for the line x + y = 2 ; y2 > y1 and the width of the shaded portion is dx.
Therefore the area,
A=∫02y2-y1dx=∫024-x2-2-xdx=12×4-x2+42sin-1×202-2x-x2202=224-22+42sin-122-024-02-42sin-102-22-222-20+022=0+2sin-11-0-0-4-2-0+0=2sin-11-2=2×π2-2=π-2

Q44.

Let R=x, y : x29+y24≤1≤x3+y2R1=x,y : x29+y24≤1 and R2=x,y : 1 ≤x3+y2∴R=R1∩ R2x29+y24=1 represents an ellipse, with centre at O(0, 0) , cutting the coordinate axis at A3, 0, A’-3, 0, B0, 2 and B’0, -2Hence, R1 is area interior to the ellipse x3+y2=1⇒2x+3y=6 represents a straight line cutting the coordinate axis at A3, 0 and B0, 2Hence,R2 will be area above the line⇒A3, 0 and B0, 2 are points of intersection of ellipse and straight line.Area of shaded region,A=∫0341-x29-21-x3 dx=∫0336-4×29-6-2x3dx=13∫0329-x2-6-2x dx=132×12×9-x2+12×9 sin-1×3-6x-2×2203=13×9-x2+9 sin-1×3-6x+x203=130+9sin-11-18+9-0 =139π2-9=3π2 -3 sq units

Q45.

x-1≤y≤5-x2x-1=5-x2x=2,-1A=∫-125-x2-x-1dx=∫-125-x2+∫-11x-1dx+∫121-xdx=x25-x2+52sin-1×5-12+x22-x-11+x-x2212=52sin-125+sin-115+12

Q46.

A(4, 1), B(6, 6) and C(8, 4) are three given points.
Equation of AB is given byy-1 =6-16-4x-4⇒y-1 =52x-4⇒y=52x-9 …..1Equation of BC is given byy-6 =4-68-6 x-6⇒y-6 =-x-6⇒y=-x+12 …..2Equation of CA is given by⇒y-4=1-44-8x-8⇒y-4=34x-8⇒y=34x-2 …..3
Required area of shaded region ABC
Shaded areaABC = areaABD + areaDBC Consider a point Px, y2on AB and Qx, y1 on AD⇒for a vertical strip of length =y2-y1 and width= dx, area =y2-y1dx,The approximating rectangle moves from x=4 to x=6Hence areaABD =∫46y2-y1dx=∫4652x-9-34x-2dx=∫4674x-7dx=74×x22-7×46=7836-16-76-4=78×20 -14=352-14=35-282 =72 sq units

Consider a point Sx, y4 on BC and Rx, y3 on DC For a vertical strip of length =y4-y3 and width= dx, area =y4-y3dx,The approximating rectangle moves from x=6 to x=8⇒area BDC=∫68-x+12-34x-2 dx=∫68-74x +14dx=- 74×x22 +14×68=- 7×28+14×68=-7864-36 +148-6=-78×28 +28=28 8=7 2Thus required areaABC=72+72=7 sq. units

Q47.

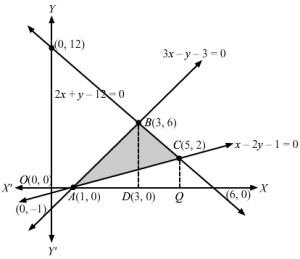
We have,

3x -y-3=0 ⋯12x+y-12=0 …2x-2y -1=0 …3
Solving 1 and 2, we get, 5x-15=0 ⇒x=3 ∴y =6B(3,6) is point of intersection of 1 and 2Solving 1 and 3, we get, 5x=5⇒x=1 ∴y=0A1,0 is point of intersection of 1 and 3Solving 2 and 3, we get, 5x=25 ⇒x=5 ∴y=2C5,2 is point of intersection of 2 and 3Now, Area ABC =area bound by 1 between x=1 and x=3 +area bound by 2 between x=3 and x=5 -area bound by 3 between x=1 and x=5 =∫133x-3 dx+∫3512-2xdx-∫15x-12dx =3×x22-3×13+12x-2×x2235-12×22-x15 =3×22-x13+12x-x235-12×22-x15 =392-3-312-1+12-25-12-9-12252-1-12-1 =6+8-4 =10 sq units

Q48.

x2 + y2 =16 represents a circle with centre O(0,0) and cutting the x axis at A(4,0)

y=3 x represents straight passing through O(0,0)

Point of intersection is obtained by solving the two equations

x2+y2 =16 and y=3 x ⇒x2+3 x2 =16⇒4×2 =16 ⇒x=±2⇒y =±23B2 ,23 and B’-2 ,-23 are points of intersection of circle and straight lineShaded areaOBQAO= areaOBPO+area PBQAP =∫023 x dx+∫2416-x2 dx =3×2202+12×16-x2+162sin-1×424 =23 +8×π2-23-8×π6 =23 +4π-23-4π3 =8π3 sq units Area bound by the circle and straight line above x axis =23 +-23+8×2π6 =8π3 sq units

Q49.

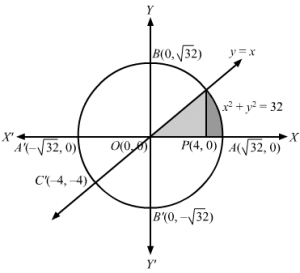
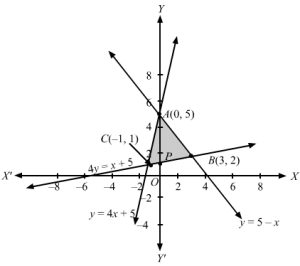
x2+y2 =4 represents a circle with centre O(0,0) and radius 2 , cutting x axis at A(2,0) and A'(-2,0)

x=3 y represents a straight line passing through O(0,0)

Solving the two equations we get

Q50.

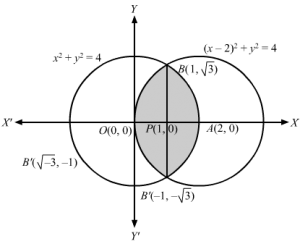
x2+ y2 = 4 …….(1) represents a circle with centre O(0,0) and radius 2
x-22+y2 = 4 ……(2) represents a circle with centre A(2 ,0) and radius 2

Points of intersection of two circles is given by solving the equations

Page 21.56 Ex.21.4

Q1.

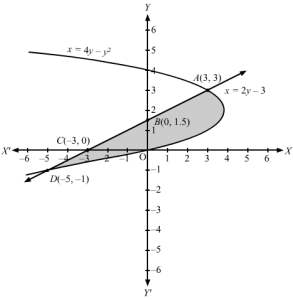
To find the point of intersection of the parabola x = 4y − y² and the line x = 2y − 3
Let us substitute x = 2y − 3 in the equation of the parabola.
2y-3=4y-y2⇒y2-2y-3=0⇒y+1y-3⇒y=-1, 3
Therefore, the points of intersection are D(−1, −5) and A(3, 3).
The area of the required region ABCDOA,
A=∫-13×1-x2 dy where, x1=4y-y2 and x2=2y-3=∫-13×1-x2 dy ∵x1>x2=∫-134y-y2-2y-3 dy=∫-134y-y2-2y+3 dy=∫-13-y2+2y+3dy=-y33+2y22+3y-13=-y33+y2+3y-13=-333+32+9-13+1-3=-32+32+9-13-1+3=11-13=323 sq. units

Q2.

The parabola cuts y-axis at (0, 4) and (0, −2).
Also, the points of intersection of the parabola and the lines y = 3 and y = −1 are B(5, 3) and D(5, −1) respectively.
Therefore, the area of the required region ABCDE
A=∫-13x dy=∫-138+2y-y2dy=8y+y2-y33-13=83+32-333-8-1+-12–133=24+9-9–8+1+13=24–7+13=24+7-13=31-13=923 sq. units

Q3.

To find the points of intersection between the parabola and the line let us substitute y = 2x − 4 in y2 = 4x.
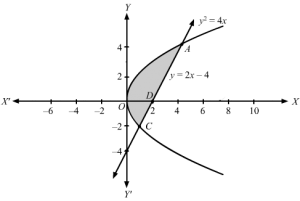
2x-42=4x⇒4×2+16-16x=4x⇒4×2-20x+16=0⇒x2-5x+4=0⇒x-1x-4=0⇒x=1, 4
⇒y=-2, 4
Therefore, the points of intersection are C(1, −2) and A(4, 4).

(i) Using Horizontal Strips:
The area of the required region ABCD
A=∫-24×1-x2dy where, x1=y+42 and x2=y24=∫-24y+42-y24 dy=y24+2y-y312-24=424+2×4-4312–224+2-2–2312=4+8-163-1-4+23=12-163+3-23=15-183=15-183=15-6=9 sq. units
(ii) Using Vertical Strips:
The area of the required region ABCD
A=∫04y2dx-∫14y1dx Where, y2=2x and y1=2x-4
=∫042xdx-∫142x-4dx=43×3204-x2-4×14=43432-43032-42-4×4-12-4×1=323-0-0-1-4=323-3=233 square units

Page 21.56 (Multiple Choice Questions)

Q1.

Answer :

(b) 1
The area bounded by the curves y=2kx, x=0, and x=2 is given by ∫022kxdx.
It is given that ∫022kxdx=3loge2

⇒1k2kxloge202=3loge2⇒1k2k2loge2-2k0loge2=3loge2⇒1k22kloge2-1loge2=3loge2⇒1k22k-1=3⇒22k-1=3k⇒22k-3k-1=0⇒k=1

Clearly, k = 1 satisfies the equation.Hence, k = 1

Q2.

Answer :

We have,x=y24 …..1×2=4y …..2
Points of intersection of two parabola is given by,
y242=4y⇒y4-64y=0⇒yy3-64=0⇒y=0, 4⇒x=0, 4

Therefore, the points of intersection are A(0, 0) and C(4, 4).

Therefore, the area of the required region ABCD,

=∫04y1-y2dx where, y1=2x and y2=x24=∫042x-x24 dx=2×2×323-x31204=2×24323-4312-2×20323-0312=323-163-0=163 square units

Q3.

Answer :

(b) 1 sq. units

The point of intersection of the curve and the straight line is A(e, 1).
Therefore, the area of the required region ABC,
A=∫01×1-x2 dy where, x1=e and x2=ey=∫01e-eydy=ey-ey01=e1-e1-e0-e0=e-e+1=1 square unit

Q4.

Answer :

b. 92 sq. units

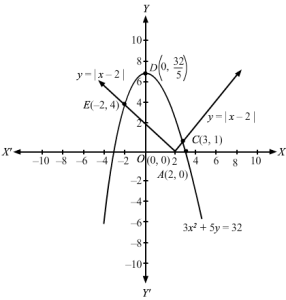
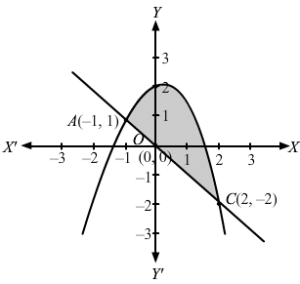
To find the points of intersection of x + y = 0 and y = 2 − x².
We put x = − y in y = 2 − x², we get

y=2-y2⇒y2+y-2=0⇒y-1y+2=0⇒y=1, -2
⇒x=-1, 2
Therefore, the points of intersection are A(−1, 1) and C(2, −2).

The area of the required region ABCD,

A=∫-12y1-y2dx Where, y1=2-x2 and y2=-x=∫-122-x2+x dx=2x-x33+x22-12=22-233+222-2-1–133+-122=4-83+2–2+13+12=6-83+2-13-12=8-93-12=5-12=92 square units.

Q5.

Answer :

b. 323

The points of intersection of the parabola and the y-axis are A(0, 2) and C(0, −2).
Therefore, the area of the required region ABCO,
A=∫-22x dy=∫-224-y2 dy=4y-y33-22=42-233-4-2–233=8-83–8+83=8-83+8-83=16-163=323 square units

Q6.

Answer :

(a) A_n + A_n −2 = 1n-1
An=Area bounded by the curve y=tanxn=tannx and the lines x=0, y=0, and x=π4.

Therefore,

An=∫0π4tannxdx⇒An-2=∫0π4tann-2xdx
Consider, An=∫0π4tannxdx
⇒An=∫0π4tann-2xtan2xdx⇒An=∫0π4tann-2xsec2x-1dx⇒An=∫0π4tann-2xsec2x-tann-2xdx⇒An=∫0π4tann-2xsec2xdx-∫0π4tann-2xdx
⇒An+An-2=∫0π4tann-2xsec2xdx

Now, An+An-2=∫0π4tann-2xsec2xdx

Let u=tanx⇒du=sec2xdx
Also, when x=0, u=0 and when x=π4, u=1

Therefore,

An+An-2=∫0π4tann-2xsec2xdx
=∫01un-2du=un-1n-101=1n-1-0=1n-1

Page 21.57 (Multiple Choice Questions)

Q7.

Answer :

c) π6-3-18

We have,x2+y2-6x-4y+12≤0y≤xx≤52Following are the corresponding equations of the given inequation.x2+y2-6x-4y+12=0 …..1y=x …..2x=52 …..3
Here, ABC is our required region in which point A is intersection of (1) and (3), point B is intersection of (1) and (2) and point C is intersection of (2) and (3).
By solving (1), (2) and (3) we get the coordinates of B and C as
B≡2, 2C≡52, 52
Now, the equation of the circle is,
x2+y2-6x-4y+12=0⇒x-32+y-22=1⇒y-22=1-x-32⇒y-2=±1-x-32⇒y=±1-x-32+2⇒y=1-x-32 +2 or -1-x-32+ 2y=1-x-32 +2 is not possible,Therefore, y=-1-x-32+ 2
The area of the required region ABC,
A=∫252y2-y1 dx Where, y1=-1-x-32+2 and y2=x=∫252x–1-x-32+2 dx=∫252x+1-x-32-2 dx=x22+x-321-x-32+12sin-1x-3-2×252=5222+52-321-52-32+12sin-152-3-252-222+2-321-2-32+12sin-12-3-22=258-141-14+12sin-1-12-5-2-12×0+12sin-1-1-4=-158-38+12×-π6-+12×-π2-2=-158-38-π12+π4+2=π6-3-18

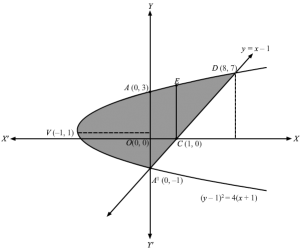
Q8.

Answer :

(a) 2

The point of intersection of the curves y=logex+e and x=loge1y is (0, 1)
y=logex+e⇒x+e=ey⇒x=ey-eHere taking, x1=ey-eand x2=loge1y
Therefore, area of the required region,
A=∫01×2-x1dy Where, x1=ey-e and x2=loge1yA=∫01loge1ydy-∫01ey-edyA=∫01loge1ydy-ey-ey01 …..1Let I=∫loge1ydyPutting 1y=t⇒-1y2dy=dt⇒dy=-y2 dt⇒dy=-1t2 dtTherefore, integral becomesI=∫-1t2 loget dt=-loge t ∫1t2dt-∫1t×1tdt=1 tloge t+1t=y loge 1y+yNow, 1 becomesA=y loge 1y+y01-ey-ey01 =y loge1y+y-ey+ey01=loge1+1-e1+e1-0+0-e0+e0=2

Q9.

Answer :

The tangent passes through the point with ordinate 3, so substituting y = 3 in equation of parabola (y − 2)2 = x − 1, we get x = 2
Therefore, the line touches the parabola at (2, 3).
We have,
y-22=x-1⇒y-2=x-1⇒y=x-1+2
Slope of the tangent of parabola at x = 2
dydxx=2=12x-1x=2=12
Therefore, the equation of the tangent is given as:
y-y0=mx-x0⇒y-3=12x-2⇒y=12x+2
Therefore, area of the required region ABC,
A=∫03×1-x2dy Where, x1=y-22+1 and x2=2y-2=∫03×1-x2dy=∫03y-22+1-2y-2dy=∫03y-2-12dy=∫03y-32dy=y-33303=3-333-0-333=9

Therefore the answer is (d)

Q10.

Answer :

(a) 2 sq. units

The required area ABC,
A=∫0πy dx=∫0πsinxdx=-cosx0π=-cosπ+cos0=1+1=2 square units

Q11.

Answer :

b) 16a23

To find the point of intersection of the parabolas substitute y=x24a in y2=4ax we get
x416a2=4ax⇒x4-64a3x=0⇒xx3-64a3=0⇒x=0 or x=4a⇒y=0 or y=4a
Therefore, the required area ABCD,
A=∫04ay1-y2dx Where, y1=2ax and y2=x24a=∫04a2ax-x24adx=4a3x32-x312a04a=4a34a32-4a312a-4a3032-0312a=4a38a32-64a312a-0=32a23-16a23=16a23 square units

Q12.

Answer :

b) 9130

Clearly, from the figure the minimum value of y is 3 when x = 0 or 1.
Therefore, the required area ABCD,
A=∫01y dx Where, y=x4-2×3+x2+3=∫01×4-2×3+x2+3dx=x55-2×44+x33+3×01=155-2144+133+31-055-2044+033+30=15-12+13+3-0=6-15+10+9030=9130 square units

Q13.

Answer :

b) 43a2

Clearly, the latusrectum passes x-axis through the point D(a, 0).
Therefore, the required area ABCD,
A=∫0ay dx Where, y=2ax=∫012ax dx=4a3x320a=4a3a32-4a3032=43a2 square units

Q14.

Answer :

Non of the given option is correct.

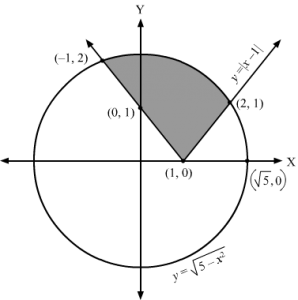
To find the points of intersection of the line and the circle substitute y = 1 − x in x2 + y2 = 1,we get A(0, 1) and B(1, 0).

Therefore, the required area of the shaded region,

A=∫01y1-y2 dx Where, y1=1-x2 and y2=1-x=∫011-x2-1-x dx==∫011-x2-1+x dx=x21-x2+12sin-1x-x+x2201=121-12+12sin-11-1+122-021-02+12sin-10-0+022=π4-12 square units

Q15.

Answer :

c) 323 sq. units

Common region of two given parabola y = 2xsup>2 and y = xsup>2 + 4 is infinite as we see in the figure here.
Therefore, area common to these two parabola is infinity.

DISCLAIMER:
In the question, instead of
“The area common to the parabola y = 2xsup>2 and y = xsup>2 + 4 is”
It should be
“The closed area made by the parabola y = 2xsup>2 and y = xsup>2 + 4 is”
Solution of this question is as follow.

To find the point of intersection of the parabolas equate the equations y = 2xsup>2 and y = xsup>2 + 4 we get

2×2=x2+4⇒x2=4⇒x=±2∴y=8

Therefore, the points of intersection are A(−2, 8) and C(2, 8).

Therefore, the required area ABCD,
A=∫-22y1-y2dx Where, y1=x2+4 and y2=2×2=∫-22×2+4-2×2 dx=∫-224-x2 dx=4x-x33-22=42-233-4-2–233=8-83–8+83=8-83+8-83=16-163=323 square units

Q16.

Answer :

d) 92

To find the point of intersection of the parabola y = xsup>2 + 1 and the line x + y = 3 substitute y = 3 − x in y = xsup>2 + 1
3-x=x2+1⇒x2+x-2=0⇒x-1x+2=0⇒x=1 or x=-2∴y=2 or y=5
So, we get the points of intersection A(−2, 5) and C(1, 2).
Therefore, the required area ABC,
A=∫-21y1-y2dx Where, y1=3-x and y2=x2+1=∫-213-x-x2+1dx=∫-213-x-x2-1dx=∫-212-x-x2dx=2x-x22-x33-21=21-122-133-2-2–222–233=2-12-13–4-2+83=2-12-13+4+2-83=8-12-93=5-12=92 square units

Q17.

Answer :

(d) none of these

The line x=π3 meets the curve y=cos x at Bπ3, 12
Area between the curve y = cos x and x-axis from x =0 and x = π3 is,
A1=∫0π3y1dx Where, y1=cosx=∫0π3cosxdx=sinx0π3=sinπ3-sin0=32

The line x=π3 meets the curve y=cos 2x at B’π3, -12

Area between the curve y = cos 2x and x-axis from x =0 and x = π3 is,
A2=∫0π4y2 dx-∫π4π3y2 dx Where, y2 = cos 2x=∫0π4cos 2x dx-∫π4π3cos 2x dx=12sin 2×0π4-12sin 2xπ4π3=12sin π2-sin 0-12sin 2π3-sin π2=12-1232-1=12-34+12=1-34=4-34

Therefore the ratios will be

A1:A2=A1A2=324-34=234-3

Q18.

Answer :

(d) 4

Required shaded area,A=∫0π2cos x dx+∫π23π2-cos x dx+∫3π22πcos x dx=∫0π2cos x dx-∫π23π2cos x dx+∫3π22πcos x dx=sinx 0π2-sinx π23π2+sinx 3π22π=sinx 0π2-sinx π23π2+sinx 3π22π=1-0–1-1+0–1=1+2+1=4 sq units

Q19.

Answer :

Disclaimer : Non of the given option is correct

Point of intersection is obtained by solving the equation of parabola ysup>2 = x and equation of line 2y = x, we have
y2=x and 2y =x⇒y2=2y ⇒y2-2y =0⇒y =0 or y=2⇒x=0 or x=4Thus O0, 0 and A4, 2 are the points of intersection of the curve and straight line. Area bound by them A=∫04y1-y2 dx Where, y1=x and y2=x2=∫04x-x2 dx=x3232-12×x2204=23×32-x2404=23432-14×42 -0=23×23-164=163-4=16-123=43 sq units

Q20.

Answer :

c) 323 sq. units

Point of intersection of parabola y = 4x − x2 with x-axis is given by
y=4x-x2 and y=0 Equation of x axis⇒4x-x2=0⇒x=0 or x=4 ⇒y=0 , y=0 Thus O0, 0 and B4, 0 are points of intersection of parabola and x-axis.Required shaded area =∫044x -x2 dx =2 x2-x3304 =2×16-643-0 =96-643 =323 square units

Page 21.58 (Multiple Choice Questions)

Q21.

Answer :

y2 2a−x=x3y=x32a−x
Let x = 2a sin2θ
dx = 4a sinθ cosθ dθ

Area= ∫02ax32a−xdx=∫0π28a3sin6θ2a cos2θ ·4a sinθ cosθ dθ=8a2∫0π2sin6θ sinθ dθ=8a2∫0π2sin4θ dθ=8a2∫0π2sin2θ1−cos2θ dθ=8a2∫0π21−cos2θ2 dθ−14∫0π2sin22θ dθ=8a2 12θ0π2−sin2θ40π2−14∫0π21−cos 4θ2dθ=8a2 π4−0−14π4−0=8a2 π4−π16=32πa2

Q22.

Answer :

(b) 2/3

Point of intersection of the parabola x2 = 4y and straight line x = 2 is given by
x2=4y and x=2⇒4=4y⇒y=1A2, 1 is the point of intersection of the curve and straight lineArea of shaded region OAB=∫02y dx =∫02×24 dx =x31202 =2312 -0 =23 square units

Q23.

Answer :

y=fx If A is the the area bound by the curve , x-axis , x=1 and x=b ⇒∫1bfx dx =A1b=b-1sin 3b+4 Given⇒fx=ddxx-1sin3x+4=sin3x+4ddxx-1 +x-1ddxsin3x+4=sin3x+4+3x-1cos3x+4

Q24.

Answer :

Non of the given option is correct.

Point of intersection of both the parabolas y2 = 8x and x2 = 8y is obtained by solving the two equations

y2=8x and x2=8y ∴y464-8y=0⇒yy3-83-0⇒y=0 or y=8⇒x=0 or x=8 ∴O0, 0 and A8, 8 are the points of intersection. Area of the shaded region =∫08y2-y1 dx =∫08y2-y1dx =∫088x-x28dx =832×32-18×x3308 =23×8×832-18×833-0 =23×8×88 -823 =23×82-823 =8232-1 =643 sq units

Q25.

Answer :

a) 163

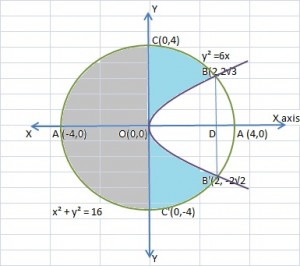
y² = 8x represents a parabola opening side ways , with vertex at O(0, 0) and Focus at B(2, 0)

Thus AA’ represents the latus rectum of the parabola.

The points of intersection of the parabola and latus rectum are A(2, 4) and A'(2, −4)

Area bound by curve , x-axis and latus rectum is the area OABO,

The approximating rectangle of width =dx and length=y has area =y dx, and moves from x=0 to x=2area OABO =∫02y dx=∫02y dx y>0 ,⇒y=y=∫028xdx=22∫02xdx=22×323202=22×23232-0=423×22=163 sq units

Q26.

Answer :

d) 174

x=-2 and x=1 intersect the curve y = x3 at A-2, -8 and B 1, 1 respectivelyIf Px, y1 lies on OA & Q x, y2 lies on curve OB Then, y1>0 ⇒y1 =y1& y2<0⇒y2 = -y2Area of curve bound by the two lines=shaded area OADO + Shaded area OCBO=∫-20y2 dx +∫01y1dx=∫-20-y2dx +∫01y1dx=∫-20-x3 dx +∫01×3 dx=-x44-20+x4401=0–164 +14-0=4+14=174 sq units

Q27.

Answer :

c) 23

The given equation of the curve is
y= x x⇒y = x2 x≥0-x2 x<0Now, solving x=1 and y=xx we getx=1 ⇒y=1 ⇒A1, 1 is point of intersection of the cuve y=xx and x=1Also, solving x=-1 and y=xx we getx=-1 ⇒y=-1⇒A’-1, -1 is point of intersection of the cuve y=xx and x=-1If Px, y1 , x>0 is a point on y= x x then y1>0 ⇒ y1 =y1 And Qx, y2 , x<0 is a point on y= x x then y2<0 ⇒y2 = -y2Required area =∫-10y2 dx +∫01y1 dx=∫-10-y2 dx +∫01y1 dx=∫-10–x2 dx +∫01×2 dx=∫-10×2 dx +∫01×2 dx=x33-10+x3301=0–133 +133-0=13+13=23 sq units

Q28.

Answer :

(b) 2-1

Points of intersection is obtained by solving y=sinx and y=cos x ∴sin x= cos x⇒x=π4 Thus the two functions intesect at x= π4 ⇒ y=sin π4 =12Hence Aπ4 , 12 is the point of intersection.∴Area bound by the curves and the y-axis when 0≤x≤π2,A =∫012 x1 dy +∫121×2 dy=∫012 x1 dy +∫121x2dy=∫0 12sin-1y dy +∫121cos-1 y dy=y sin-1 y +1-y2012+y cos -1y-1-y2121=12sin-1 12+1-12 – 1+1×cos -11-0-12cos -112+1-12 = 12×π4 +12 -1 +0-12×π4 +12=12+12-1=22-1=2-1 sq units

Q29.

Answer :

Points of intersection of the parabola and the circle is obtained by solving the simultaneous equations

x2+y2=16 and y2=6x⇒x2+6x=16 ⇒x2+6x-16 =0⇒x+8x-2=0⇒x=2 or x=-8 x can not be -8 as in this case it will be the point outside circle.∴x=2∴ When x=2, y=±6×2 =±12=±23∴B2 , 23 and B’2 , -23 are points of intersection of the parabola and circle. Required area = AreaOB’C’A’CBO= area of circle-areaOBAB’O Area of circle with radius 4 =π×42=16π Now, AreaOBAB’O =2areaOBAO =2areaOBDO+areaDBAD =2×∫026x dx +∫2416-x2 dx =2×6×323202+x216-x2 +12×16 sin-1×424 =2× 6×23×232-0 +12416-42 +12×16 sin-144-2216-22 -12×16 sin-124 =2 × 6×23×22+0+8 sin-11-12 -8 sin-112 =2×833+8×π2-23-8π6 =2 83-633+8π2-π6 =2233+82π6 =433+16π3Shaded area =16π-433+16π3=48π-16π3- 433=32π3- 433=438π-3 sq units

Q30.

Answer :

(b) π − 2

We have, x2 + y2 = 4 represents a circle with centre at O(0,0) and radius 2
x + y = 2 represents a straight line cutting the x-axis at A(2, 0) and y axis at B(0, 2)

Thus , A (2,0) and B(0,2) are also the points of intersection of the straight line and the circle

Smaller area enclosed by the curve and straight line is the shaded area

Shaded area ABCA=areaOBCA – areaOBAO =∫024-x2 dx -∫022-xdx ∵x2+y2=4⇒y=4-x2 and x+y=2⇒y=2-x=∫024-x2 +x-2dx=12×4-x2 +12×4×sin-1×2 +x22-2×02=12×24-22 +2×sin-122 +222-2×2-0 =0+2×π2+2-4 =π-2 sq units

Q31.

Answer :

b) 13

The points of intersection of the straight line and the parabola is obtained by solving the simultaneous equations
y2=4x and y=2x⇒2×2=4x⇒4×2=4x⇒xx-1=0⇒x=0 or x=1⇒y=0 or y=2Thus O0, 0 and A1, 2 are the points of intersection of the parabola and straight lineShaded area is the required area.Using the horizontal strip method ,Shaded area =∫02×2-x1dy =∫02y2-y24 dy =12y22-14y3302 =1422 -11223-0 =1-812 =12-812 =13 sq. units

Q32.

Answer :

(a) π

x2 + y2 = 4 represents a circle with centre at origin O(0, 0) and radius 2 units, cutting the coordinate axis at A, A’, B and B’.
x = 2 represents a straight line parallel to the y-axis, intersecting the circle at A(2, 0)
x = 0 represents the y-axis
Area bounded by the circle and the two given lines in the first quadrant is the shaded area OBCAO
AreaOBCAO=∫02y dx =∫024-x2 dx =12×4-x2 +12×4 sin-1×202 =12×24-22 +12×4 sin-122 -0 =0+2sin-11 =2×π2 =π sq units

Q33.

Answer :

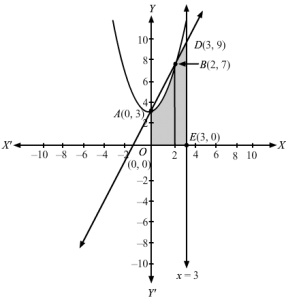
b) 94

y² = 4x represents a parabola with vertex at origin O(0, 0) and symmetric about +ve x-axis

y = 3 is a straight line parallel to the x-axis

Point of intersection of the line and the parabola is given by
Substituting y = 3 in the equation of the parabola
y2=4x⇒32=4x⇒x=94Thus A94 , 3 is the point of intersection of the parabola and straight line.

Required area is the shaded area OABO

Using the horizontal strip method , AreaOABO=∫03x dy =∫03y24 dy =14y3303 =3312 =94 sq. units

Page 21.13 Ex.21.1

Page 21.14 Ex.21.1

Page 21.15 Ex.21.1

Page 21.21 Ex.21.2

Page 21.22 Ex.21.2

Page 21.47 Ex.21.3

Page 21.49 Ex.21.3

Page 21.56 Ex.21.4

Page 21.56 (Multiple Choice Questions)

Page 21.57 (Multiple Choice Questions)

Page 21.58 (Multiple Choice Questions)

Leave a Reply Cancel reply