Page 30.14 Ex.30.1
Q1.
Answer :
Let x and y number of gadgets A and B respectively being produced in order to maximize the profit.
Since, each unit of gadget A takes 10 hours to be produced by machine A and 6 hours to be produced by machine B and each unit of gadget B takes 5 hours to be produced by machine A and 4 hours to be produced by machine B.
Therefore, the total time taken by the Foundry to produce x units of gadget A and y units of gadget B is 10x+6y. This must be less than or equal to the total hours available.
Hence, 10x + 6y ≤ 1000.
This is our first constraint.
The total time taken by the machine-shop to produce x units of gadget A and y units of gadget B is 5x + 4y. This must be less than or equal to the total hours available.
Hence, 5x + 4y ≤ 600
This is our second constraint.
Since x and y are non negative integers, therefore x, y ≥ 0
It is given that the profit on the sale of A is Rs 30 per unit as compared with Rs 20 per unit of B. Therefore, profit gained on x and y number of gadgets A and B is Rs 30x and Rs 20y respectively.
Let Z denotes the total cost
Therefore, Z= Rs (30x + 20y)
Hence, the above LPP can be stated mathematically as follows:
Maximize Z = 30x + 20y
subject to
10x + 6y ≤ 1000,
5x + 4y ≤ 600
x, y ≥ 0
Q2.
Answer :
Let the company produces x units of product A and y units of product B.
Since, each unit of product A costs Rs 60 and each unit of product B costs Rs 80.Therefore, x units of product A and y units of product B will cost Rs 60x and Rs 80y respectively.
Let Z denotes the total cost.
∴ Z = Rs (60x + 80y)
Also, one unit of product A requires one machine hour.
The total machine hours available with the company for product A are 400 hours.
Therefore, x≤400
This is our first constraint
Also,one unit of product A and B require 1 labour hour each and there are a total of 500 labours hours.
Thus, x+y≤500
This is our second constraint.
Since, x and y are non negative integers, therefore x, y ≥ 0
Also, as per agreement, the company has to supply atleast 200 units of product B to its regular customers.
∴y≥200
Hence, the required LPP is as follows:
Minimize Z = 60x + 80y
subject to
x ≤ 400,
x + y ≤ 500
y≥200
x, y ≥ 0
Q3.
Answer :
Let the number of units of product A, B and C manufactured be x, y and z respectively.
Given, machine M1 takes 4 minutes to manufacture 1 unit of product A, 3 minutes to manufacture one unit of product B and 5 minute to manufacture one unit of product C.
Machine M2 takes 2 minutes to manufacture 1 unit of product A, 2 minutes to manufacture one unit of product B and 4 minute to manufacture one unit of product C.
The availability is 2000 minutes for M1 and 2500 minutes for M2
Thus,
4x+3y+5z≤20002x+2y+4z≤2500
Number of units of products cannot be negative.
So, x, y, z≥0
Further, it is given that the firm should manufacture 100 A’s, 200 B’s and 50 C’s but not more than 150 A’s.
Then,
100≤x≤150y≥200z≥50
Let Z denotes the profit
∴ Z=3x + 2y + 4z
Hence, the required LPP is as follows :
Maximize Z=3x + 2y + 4z
subject to
4x+3y+5z≤20002x+2y+4z≤2500
100≤x≤150y≥200z≥50x, y, z≥0
Page 30.15 Ex.30.1
Q4.
Answer :
Let the firm produces x units of product A and y units of product B.
Since, each unit of product A requires one minute on machine M1 and two minutes on machine M2.
Therefore, x units of product A will require product x minutes on machine M1 and 2x minutes on machine M2
Also,
Since each unit of product B requires one minute on machine M1 and one minute on machine M2.
Therefore, y units of product A will require product y minutes on machine M1 and y minutes on machine M2
It is given that the machine M1 is available for 6 hours and 40 minutes i.e. 400 minutes and machine M2 is available for 10 hours i.e. 600 minutes
Thus,
x+y≤4002x+y≤600
Since,units of the products cannot be negative,so x, y ≥ 0
Let Z denotes the total profit
∴ Z=2x+3y which is to be maximised
Hence, the required LPP is as follows:
Maximize Z = 2x + 3y
subject to
x+y≤4002x+y≤600
x, y ≥ 0
Q5.
Answer :
Let plant I be run for x days and plant II be run for y days
Then,
| Tyres | Plant I (x) | Plant II (y) | Demand |
| A | 50 | 60 | 2500 |
| B | 100 | 60 | 3000 |
| C | 100 | 200 | 7000 |
Minimum demand for Tyres A,B and C is 2500, 3000 and 7000 respectively.The demand can be more than the minimum demand.
Therefore,the inequations will be
50x+60y≥2500100x+60y≥3000
100x+200y≥7000
Also, the objective function is Z = 2500x + 3500y
Hence, the required LPP is as follows:
Minimise Z = 2500x + 3500y
subject to
50x+60y≥2500100x+60y≥3000
100x+200y≥7000
Q6.
Answer :
Let x units of product A and y units of product B be produced.
Then,
Since, it takes 5 hours to produce a unit of A and 3 hours to produce a unit of B.
Therefore, it will take 5x hours to produce x units of A and 3y hours to produce y units of B.
As, the total capacity is of 45000 man hours.
⇒5x+3y≤45000
Also,
The maximum number of units of A that can be sold is 7000 and that of B is 10,000 and number of units cannot be negative.
Thus, 0≤x≤7000, 0≤y≤10000
Now,
Total profit = 60x+40y
Here, we need to maximize profit
Thus, the objective function will be maximize Z=60x + 40y
Hence, the required LPP is as follows:
Maximize Z = 60x + 40y
subject to
5x+3y≤45000x≤7000y≤10000x, y≥0
Q7.
Answer :
Let the person takes x lbs and y lbs of food I and II respectively that were taken in the diet.
Since, per lb of food I costs Rs 60 and that of food II costs Rs 100.
Therefore, x lbs of food I costs Rs 60x and y lbs of food II costs Rs 100y.
Total cost per day = Rs (60x + 100y)
Let Z denote the total cost per day
Then, Z = 60x + 100y
Total amount of calcium in the diet is 10x+5y
Since, each lb of food I contains 10 units of calcium.Therefore, x lbs of food I contains 10x units of calcium.
Each lb of food II contains 5 units of calciu.So,y lbs of food II contains 5y units of calcium.
Thus, x lbs of food I and y lbs of food II contains 10x + 5y units of calcium.
But, the minimum requirement is 20 lbs of calcium.
∴ 10x+5y≥20
Since, each lb of food I contains 5 units of protein.Therefore, x lbs of food I contains 5x units of protein.
Each lb of food II contains 4 units of protein.So,y lbs of food II contains 4y units of protein.
Thus, x lbs of food I and y lbs of food II contains 5x + 4y units of protein.
But, the minimum requirement is 20 lbs of protein.
∴ 5x+4y ≥ 20
Since, each lb of food I contains 2 units of calories.Therefore, x lbs of food I contains 2x units of calories.
Each lb of food II contains units of calories.So,y lbs of food II contains 6y units of calories.
Thus, x lbs of food I and y lbs of food II contains 2x + 6y units of calories.
But, the minimum requirement is 13 lbs of calories.
∴2x+6y≥13
Finally, the quantities of food I and food II are non negative values.
So, x, y ≥ 0
Hence, the required LPP is as follows:
Min Z = 60x + 100y
subject to
10x+5y≥205x+4y≥202x+6y≥13x, y≥0
Page 30.16 Ex.30.1
Q8.
Answer :
Let x and y units of products A and B were manufactured respectively.
The contribution to profit is Rs 2 for each unit of A and Rs 3 for each unit of B.
Therefore for x units of A and y units of B,the contribution to profit would be Rs 2x and Rs 3y respectively.
Let Z denote the total profit
Then, Z = Rs (2x + 3y)
Total hours required for grinding, turning, assembling and testing are x+2y, 3x+y, 6x+3y, 5x+4y respectively.
The available capacities of these operations in hours for the given period are grinding 30, turning 60, assembling 200 and testing 200.
∴ x+2y≤30, 3x+y≤60, 6x+3y≤200, 5x+4y≤200
Units of products cannot be negative.Therefore,
x,y≥0
Hence, the required LPP is as follows:
Maximize Z = 2x + 3y
subject to
x+2y≤30, 3x+y≤60, 6x+3y≤200, 5x+4y≤200
Q9.
Answer :
Let x and y units of food F1 and food F2 were mixed.
Clearly, x ≥ 0 and y ≥ 0
One unit of food F1 contains 2 units of vitamin A and one unit of of food F2 contains 4 units of vitamin A. Therefore, x and y units of food F1 and food F2 respectively contains 2x and 4y units of vitamin A.
It is given that the minimum daily requirements for a person of vitamin A is 40 units.
Hence, 2x+ 4y ≥ 40
One unit of food F1 contains 3 units of vitamin B and one unit of food F2 contains 2 units of of vitamin B. Therefore, x and y units of F1 and F2 respectively contains 3x and 2y units of vitamin B.
It is given that the minimum daily requirements for a person of vitamin B is 50 units.
Hence, 3x+ 2y ≥ 50
One unit of food F1 and food F2 cost Rs 50 and 25 respectively. Therefore, x and y units of food F1 and food F2 costs Rs 50x and Rs 25y respectively.
Let Z denote the total cost
Then, Z = Rs (50x + 25y)
Hence, the required LPP is
Minimize Z = 50x + 25y
subject to
2x+ 4y ≥ 40
3x+ 2y ≥ 50
x ≥ 0,y ≥ 0
Q10.
Answer :
Let x number of trucks and y number of automobiles were produced to maximize the profit.
Since, the manufacturer makes profit of Rs 30000 on each truck and Rs 2000 on each automobile.
Therefore, on x number of trucks and y number of automobiles profit would be Rs 30000x and Rs 2000y respectively.
Total profit = Rs (30000x + 2000y)
Let Z denote the total profit
Then, Z = 30000x + 2000y
Since, 5 man-days and 2 man-days were required to produce each truck and automobile at shop A.
Therefore, 5x man-days and 2y man-days are required to produce x trucks and y automobiles at shop A.
Also,
Since 3 man-days were required to produce each truck and automobile at shop B.
Therefore, 3x man-days and 3y man-days are required to produce x trucks and y automobiles.
As, shop A has 180 man-days per week available while shop B has 135 man-days per week.
∴ 5x+2y≤180, 3x+3y≤135
Number of trucks and automobiles cannot be negative.
∴ x, y≥0
Hence, the required LPP is as follows :
Maximize Z = 30000x + 2000y
subject to
5x+2y≤180, 3x+3y≤135, x≥0, y≥0
Q11.
Answer :
Let x and y units of product A and B were manufactured respectively.
Labour cost per unit to manufacture product A and product B is Rs 16 and Rs 20 respectively.Therefore, labour cost for x and y units of product A and product B is Rs 16x and Rs 20y respectively.
Total labour cost to manufacture product A and product B is Rs (16x+20y)
Raw material cost per unit to manufacture product A and product B is Rs 4 and Rs 4 respectively.Therefore,raw material cost for x and y units of product A and product B is Rs 4x and Rs 4y respectively.
Total raw material cost to manufacture product A and product B is Rs (4x + 4y)
Hence, total cost price to manufacture product A and product B = Total labour cost + Total raw material cost
= 16x + 4x + 20y + 4y
= 20x + 24y
Selling price per unit for product A and product B is Rs 25 and Rs 30 respectively. Therefore, total selling price for product A and product B is Rs 25x and Rs 30y respectively.
Total selling price = 25x + 30y
∴ Total profit = Total selling price − Total cost price = 25x + 30y -(20x + 24y)
= 5x + 6y
Let Z denote the total profit
Then, Z = 5x+6y
One unit of product A and product B requires 3 hours and 2 hours respectively at department 1.Therefore, x units and y units of product A and product B
require 3x hours and 2y hours respectively.
The weekly capacity of department 1 is 130.
∴ 3x+2y≤130
One unit of product A and B requires 4 hours and 6 hours respectively at department 2.Therefore, x units and y units of product A and product B require 4x hours and 6y hours respectively.
The weekly capacity of department 2 is 260.
∴ 4x+6y≤260
Units of products cannot be negative.Therefore,
x, y≥0
Hence, the required LPP is as follows:
Maximize Z = 5x + 6y
subject to
3x+2y≤130, 4x+6y≤260, x≥0, y≥0
Q12.
Answer :
Let x number of model 314 planes and y number of model 535 planes were used.
It is given that cost of one model 314 plane is Rs 100000 and cost of one model 535 plane is Rs 150000.
Therefore, cost of x model 314 plane is Rs 100000x and cost of y model 535 plane is Rs 150000y.
Total cost price = 100000x + 150000y
Let Z denote the total cost
Then, Z = 100000x+150000y
Also,
Each model 314 planes have 20 first class and 30 tourist class seats and each model 535 planes has 20 first class and 60 tourist class seats.
The group needs 160 first class seats and 300 tourist class seats.
∴ 20x+20y≥160 30x+60y≥300
Number of planes cannot be negative.
Therefore, x, y≥0
Hence, the required LPP is as follows:
Min Z = 100000x+150000y
subject to
20x+20y≥160 30x+60y≥300x≥0, y≥0
Page 30.17 Ex.30.1
Q13.
Answer :
Let Amit correctly solves x problems from the first set, y problems from the second set and z problems from the third set.
Given,
Amit cannot submit more than 100 correctly solved problems.
∴ x+y+z≤100
The problem in the first set are worth 5 points each,those in the second set worth 4 points each and those in the third set worth 6 points each.
Therefore, x problems from the first set worth 5x points, y problems from the second set worth 4y points and z problems from the third set worth 6z points.
Thus, total credit points will be 5x+4y+6z.
Let Z denotes the total credit of Amit
∴ Z = 5x+4y+6z
It requires 3 minutes to solve a 5 point problem, 2 minutes to solve a 4 point problem and 4 minutes to solve a 6 point problem.Therefore,x problems from the first set require 3x minutes, y problems from the second set require 2y minutes and z problems from the third set require 4z minutes.
Thus, the total time require by Amit will be (3x + 2y + 4z) minutes.
It is given that the total time that Amit can devote on his mathematics assignment is 312hours i.e. 210 minutes.
∴ 3x+2y+4z≤210
Further, it is given that the total time that Amit can devote in solving first two types of problems cannot be more than 212 hours i.e. 150 minutes.
∴ 3x+2y≤150
Number of problems cannot be negative.Therefore,
x, y≥0
Hence, the required LPP is follows:
Maximize Z = 5x+4y+6z
subject to
x+y+z≤1003x+2y+4z≤210 3x+2y≤150x≥0, y≥0
Q14.
Answer :
Let the farmer sow tomatoes in x acres, lettuce in y acres & radishes in z acres of the farm.
Average yield per acre is 2000 kgs for tomatoes, 3000 kgs of lettuce and 1000 kg of radishes.
Thus, the farmer raised 2000x kg of tomatoes, 3000y kg of lettuce and 1000z kg of radishes.
Given, price he can obtain is Re 1 per kilogram for tomatoes, Re 0.75 a head for lettuce and Rs 2 per kilogram for radishes.
∴ Selling price = Rs 2000×1+3000y0.75+1000z2 = Rs (2000x + 2250y + 2000z)
Labour required for sowing, cultvating and harvesting per acre is 5 man-days for tomatoes and radishes and 6 man-days for lettuce.Therefore, labour required for sowing, cultivating and harvesting per acre is 5x for tomatoes, 6y for lettuce and 5z for radishes.
Number of man-days required in sowing, cultivating and harvesting= 5x+6y+5z
Price of one man-day = Rs 20
∴ Labour cost = 205x+6y+5z=100x+120y+100z
Also, fertilizer is available at Re 0.50 per kg and the amount required per acre is 100 kgs each for tomatoes and lettuce and 50 kgs for radishes.
Therefore, fertilizer required is 100x kgs for the tomatoes sown in x acres, 100y kgs for the lettuce sown in y acres and 50z kgs for radishes sown in z acres of land.
Hence, total fertilizer used= (100x + 100y +50z) kgs
Thus, fertilizer’s cost = Rs 0.5×100x+100y+50z=Rs50x+50y+25z
So, the total price that has been cost to farmer = Labour cost + Fertilizer cost
= Rs 150x+170y+125z
Profit made by farmer = Selling price – Cost price
= Rs (2000x + 2250y + 2000z)− Rs (150x + 170y + 125z)
= Rs 1850x+2080y+1875z
Let Z denotes the total profit
∴ Z =1850x+2080y+1875z
Now,
Total area of the farm = 100 acres
x+y+z≤100
Also, it is given that the total man-days available are 400.
Thus, 5x+6y+5z≤400
Area of the land cannot be negative.
Therefore, x, y≥0
Hence, the required LPP is as follows:
Maximize Z=1850x+2080y+1875z
subject to
x+y+z≤100 5x+6y+5z≤400x, y, z≥0
Q15.
Answer :
Let tailor A work for x days and tailor B work for y days.
In one day, A can stitch 6 shirts and 4 pants whereas B can stitch 10 shirts and 4 pants.
Thus, in x days A can stitch 6x shirts and 4x pants. Similarly, in y days B can stitch 10y shirts and 4y pants.
It is given that the minimum requirement of the shirts and pants are respectively 60 and 32 respectively.
Thus,
6x+10y≥604x+4y≥32
Further it is given that A and B earn Rs 150 and Rs 200 per day respectively. Thus, in x days and y days, A and B earn Rs 150x and Rs 200y respectively.
Let Z denotes the total cost
∴ Z =Rs 150x+200y
Number of days cannot be negative.
Therefore, x, y≥0
Hence, the required LPP is as follows:
Minimize Z=150x+200y
subject to
6x+10y≥604x+4y≥32x≥0, y≥0
Page 30.32 Ex.30.2
Q1.
Answer :
First, we will convert the given inequations into equations, we obtain the following equations:
3x + 5y = 15, 5x + 2y = 10, x = 0 and y = 0
Region represented by 3x + 5y ≤ 15 :
The line 3x + 5y = 15 meets the coordinate axes at A(5,0) and B(0,3) respectively. By joining these points we obtain the line 3x + 5y = 15.
Clearly (0,0) satisfies the inequation 3x + 5y ≤ 15. So,the region containing the origin represents the solution set of the inequation 3x + 5y ≤ 15.
Region represented by 5x + 2y ≤ 10 :
The line 5x + 2y = 10 meets the coordinate axes at C(2,0) and D(0,5) respectively. By joining these points we obtain the line 5x + 2y = 10.
Clearly (0,0) satisfies the inequation 5x + 2y ≤ 10. So,the region containing the origin represents the solution set of the inequation 5x + 2y ≤ 10.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints, 3x + 5y ≤ 15, 5x + 2y ≤ 10, x ≥ 0, and y ≥ 0, are as follows.
The corner points of the feasible region are O(0, 0), C(2, 0),E2019,4519 and B(0, 3).
The values of Z at these corner points are as follows.
| Corner point | Z = 5x + 3y |
| O(0, 0) | 5 × 0 + 3 × 0 = 0 |
| C(2, 0) | 5 × 2 + 3 × 0 = 10 |
| E2019,4519 | 5 ×2019+ 3 ×4519=23519 |
| B(0, 3) | 5 × 0 + 3 × 3 = 9 |
Therefore, the maximum value of Z is 23519at the point 2019,4519.Hence, x= 2019 and y =4519 is the optimal solution of the given LPP.
Thus, the optimal value of Z is 23519.
Q2.
Answer :
First, we will convert the given inequations into equations, we obtain the following equations:
2x + 3y = 13, 3x +y = 5, x = 0 and y = 0
Region represented by 2x + 3y ≤ 13 :
The line 2x + 3y = 13 meets the coordinate axes at A132,0 and B0,133 respectively. By joining these points we obtain the line 2x + 3y = 13.
Clearly (0,0) satisfies the inequation 2x + 3y ≤ 13. So,the region containing the origin represents the solution set of the inequation 2x + 3y ≤ 13.
Region represented by 3x + y ≤ 5:
The line 5x + 2y = 10 meets the coordinate axes at C53,0 and D(0, 5) respectively. By joining these points we obtain the line 3x + y = 5.
Clearly (0,0) satisfies the inequation 3x + y ≤ 5. So,the region containing the origin represents the solution set of the inequation 3x + y ≤ 5.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints, 2x + 3y ≤ 13, 3x + y ≤ 5, x ≥ 0, and y ≥ 0, are as follows.
The corner points of the feasible region are O(0, 0), C53,0 ,E27,297 and B0,133.
The values of Z at these corner points are as follows.
| Corner point | Z = 9x + 3y |
| O(0, 0) | 9 × 0 + 3 × 0 = 0 |
| C53,0 | 9 ×53+ 3 × 0 = 15 |
| E27,297 | 9 ×27+ 3 ×297= 15 |
| B0,133 | 9 × 0 + 3 ×133= 13 |
We see that the maximum value of the objective function Z is 15 which is at C 53,0 and E27,297.
Thus, the optimal value of Z is 15.
Q3.
Answer :
First, we will convert the given inequations into equations, we obtain the following equations:
4x + y = 20, 2x +3y = 30, x = 0 and y = 0
Region represented by 4x + y ≥ 20 :
The line 4x + y = 20 meets the coordinate axes at A(5, 0) and B(0, 20) respectively. By joining these points we obtain the line 4x + y = 20.
Clearly (0,0) does not satisfies the inequation 4x + y ≥ 20. So,the region in xy plane which does not contain the origin represents the solution set of the inequation 4x + y ≥ 20.
Region represented by 2x +3y ≥ 30:
The line 2x +3y = 30 meets the coordinate axes at C(15,0) and D(0, 10) respectively. By joining these points we obtain the line
2x +3y = 30.Clearly (0,0) does not satisfies the inequation 2x +3y ≥ 30. So,the region which does not contain the origin represents the solution set of the inequation 2x +3y ≥ 30.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints, 4x + y ≥ 20, 2x +3y ≥ 30, x ≥ 0, and y ≥ 0, are as follows.
The corner points of the feasible region are B(0, 20), C(15,0), E(3,8) and C(15,0).
The values of Z at these corner points are as follows.
| Corner point | Z = 18x + 10y |
| B(0, 20) | 18 × 0 + 10 × 20 = 200 |
| E(3,8) | 18 × 3 + 10 × 8 = 134 |
| C(15,0) | 18 × 15 + 10 ×0 = 270 |
Therefore, the minimum value of Z is 134 at the point E(3,8). Hence, x = 3 and y =8 is the optimal solution of the given LPP.
Thus, the optimal value of Z is 134.
Q4.
Answer :
First, we will convert the given inequations into equations, we obtain the following equations:
2x + y = 18, 3x + 2y = 34
Region represented by 2x + y ≥ 18:
The line 2x + y = 18 meets the coordinate axes at A(9, 0) and B(0, 18) respectively. By joining these points we obtain the line 2x + y = 18.
Clearly (0,0) does not satisfies the inequation 2x + y ≥ 18. So,the region in xy plane which does not contain the origin represents the solution set of the inequation 2x + y ≥ 18.
Region represented by 3x + 2y ≤ 34:
The line 3x + 2y = 34 meets the coordinate axes at C343, 0 and D(0, 17) respectively. By joining these points we obtain the line 3x + 2y = 34.
Clearly (0,0) satisfies the inequation 3x + 2y ≤ 34. So,the region containing the origin represents the solution set of the inequation 3x + 2y ≤ 34.
The corner points of the feasible region are A(9, 0), C343, 0 and E(2, 14).
The values of Z at these corner points are as follows.
| Corner point | Z = 50x + 30y |
| A(9, 0) | 50 × 9 + 3 × 0 = 450 |
| C343,0 | 50 ×343+ 30 × 0 =17003 |
| E(2, 14) | 50 × 2 + 30 × 14 = 520 |
Therefore, the maximum value of Z is 17003at the point 343, 0.Hence, x = 343 and y =0 is the optimal solution of the given LPP.
Thus, the optimal value of Z is 17003.
Q5.
Answer :
We need to maximize Z = 4x + 3y
First, we will convert the given inequations into equations, we obtain the following equations:
3x + 4y = 24, 8x + 6y = 48, x = 5, y = 6, x = 0 and y = 0.
The line 3x + 4y = 24 meets the coordinate axis at A(8, 0) and B(0,6). Join these points to obtain the line 3x + 4y = 24.
Clearly, (0, 0) satisfies the inequation 3x + 4y ≤ 24.So, the region in xy-plane that contains the origin represents the solution set of the given equation.
The line 8x + 6y = 48 meets the coordinate axis at C(6, 0) and D(0,8). Join these points to obtain the line 8x + 6y = 48.
Clearly, (0, 0) satisfies the inequation 8x + 6y ≤ 48. So, the region in xy-plane that contains the origin represents the solution set of the given equation.
x = 5 is the line passing through x = 5 parallel to the Y axis.
y = 6 is the line passing through y = 6 parallel to the X axis.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations.
These lines are drawn using a suitable scale.
The corner points of the feasible region are O(0, 0), G5, 0, F5,43, E247,247 and B0, 6.
The values of Z at these corner points are as follows.
| Corner point | Z = 4x + 3y |
| O(0, 0) | 4× 0 + 3 × 0 = 0 |
| G5, 0 | 4 × 5 + 3 × 0 = 20 |
| F5,43 | 4 × 5 + 3 ×43= 24 |
| E247,247 | 4 ×247+ 3 ×247=1967= 24 |
| B0, 6 | 4 × 0 + 3 × 6 = 18 |
We see that the maximum value of the objective function Z is 24 which is at F5,43 and E247,247.
Thus, the optimal value of Z is 24.
Q6.
Answer :
First, we will convert the given inequations into equations, we obtain the following equations:
3x + 2y = 80, 2x + 3y = 70, x = 0 and y = 0
Region represented by 3x + 2y ≤ 80 :
The line 3x + 2y = 80 meets the coordinate axes at
A803, 0
and
B0, 40
respectively. By joining these points we obtain the line 3x + 2y = 80.
Clearly (0,0) satisfies the inequation 3x + 2y ≤ 80 . So,the region containing the origin represents the solution set of the inequation 3x + 2y ≤ 80 .
Region represented by 2x + 3y ≤ 70:
The line 2x + 3y = 70 meets the coordinate axes at
C35, 0
and
D0, 703
respectively. By joining these points we obtain the line 2x + 3y ≤ 70.
Clearly (0,0) satisfies the inequation 2x + 3y ≤ 70. So,the region containing the origin represents the solution set of the inequation 2x + 3y ≤ 70.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0 and y ≥ 0.
The feasible region determined by the system of constraints, 3x + 2y ≤ 80, 2x + 3y ≤ 70, x ≥ 0, and y ≥ 0 are as follows.
The corner points of the feasible region are O(0, 0), A803, 0 ,E20, 10 and D0,703.
The values of Z at these corner points are as follows.
| Corner point | Z = 15x + 10y |
| O(0, 0) | 15 × 0 + 10 × 0 = 0 |
| A803, 0 | 15 × 803+ 10 × 0 = 400 |
| E20, 10 | 15 × 20 + 10 × 10 = 400 |
| D0,703 | 15 × 0 + 10 × 703= 7003 |
We see that the maximum value of the objective function Z is 400 which is at A803, 0 and E20, 10.
Thus, the optimal value of Z is 400.
Q7.
Answer :
First, we will convert the given inequations into equations, we obtain the following equations:
3x + y = 12, 2x + 5y = 34, x = 0 and y = 0
Region represented by 3x + y ≤ 12:
The line 3x + y = 12 meets the coordinate axes at A4, 0 and B0, 12 respectively. By joining these points we obtain the line 3x + y = 12.
Clearly (0,0) satisfies the inequation 3x + y ≤ 12. So,the region containing the origin represents the solution set of the inequation 3x + y ≤ 12 .
Region represented by 2x + 5y ≤ 34:
The line 2x + 5y = 34 meets the coordinate axes at C17, 0 and D0, 345 respectively. By joining these points we obtain the line 2x + 5y ≤ 34.
Clearly (0,0) satisfies the inequation 2x + 5y ≤ 34. So,the region containing the origin represents the solution set of the inequation 2x + 5y ≤ 34.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0 and y ≥ 0.
The feasible region determined by the system of constraints, 3x + y ≤ 12, 2x + 5y ≤ 34, x ≥ 0, and y ≥ 0 are as follows.
The corner points of the feasible region are O(0, 0), A4, 0 ,E2, 6 and D0,345.
The values of Z at these corner points are as follows:
| Corner point | Z = 10x + 6y |
| O(0, 0) | 10 × 0 + 6 × 0 = 0 |
| A4, 0 | 10× 4 + 6 × 0 = 40 |
| E2, 6 | 10 × 2 + 6 × 6 = 56 |
| D0,345 | 10 × 0 + 6 × 345= 2043 |
We see that the maximum value of the objective function Z is 56 which is at E2, 6 that means at x = 2 and y = 6.
Thus, the optimal value of Z is 56.
Q8.
Answer :
We have to maximize Z = 3x + 4y
First, we will convert the given inequations into equations, we obtain the following equations:
2x + 2y = 80, 2x + 4y = 120
Region represented by 2x + 2y ≤ 80:
The line 2x + 2y = 80 meets the coordinate axes at A40, 0 and B0, 40 respectively. By joining these points we obtain the line 2x + 2y = 80.
Clearly (0,0) satisfies the inequation 2x + 2y ≤ 80. So,the region containing the origin represents the solution set of the inequation 2x + 2y ≤ 80.
Region represented by 2x + 4y ≤ 120:
The line 2x + 4y = 120 meets the coordinate axes at C60, 0 and D0, 30 respectively. By joining these points we obtain the line 2x + 4y ≤ 120.
Clearly (0,0) satisfies the inequation 2x + 4y ≤ 120. So,the region containing the origin represents the solution set of the inequation 2x + 4y ≤ 120.
The feasible region determined by the system of constraints, 2x + 2y ≤ 80, 2x + 4y ≤ 120 are as follows:
The corner points of the feasible region are O(0, 0), A40, 0, E20, 20 and D0, 30.
The values of Z at these corner points are as follows:
| Corner point | Z = 3x + 4y |
| O(0, 0) | 3 × 0 + 4 × 0 = 0 |
| A40, 0 | 3× 40 + 4 × 0 = 120 |
| E20, 20 | 3 × 20 + 4 × 20 = 140 |
| D0, 30 | 10 × 0 + 4 ×30 = 120 |
We see that the maximum value of the objective function Z is 140 which is at E20, 20 that means at x = 20 and y = 20.
Thus, the optimal value of Z is 140.
Q9.
Answer :
We have to maximize Z = 7x + 10y
First, we will convert the given inequations into equations, we obtain the following equations:
x + y = 30000,y = 12000, x = 6000, x = y, x = 0 and y = 0.
Region represented by x + y ≤ 30000:
The line x + y = 30000 meets the coordinate axes at A30000, 0 and B0, 30000 respectively. By joining these points we obtain the line x + y = 30000.
Clearly (0,0) satisfies the inequation x + y ≤ 30000. So,the region containing the origin represents the solution set of the inequation x + y ≤ 30000.
The line y = 12000 is the line that passes through C(0,12000) and parallel to x axis.
The line x = 6000 is the line that passes through (6000, 0) and parallel to y axis.
Region represented by x ≥ y
The line x = y is the line that passes through origin.The points to the right of the line x = y satisfy the inequation x ≥ y.
Like by taking the point (−12000, 6000).Here, 6000 > −12000 which implies y > x. Hence, the points to the left of the line x = y will not satisfy the given inequation x ≥ y.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0 and y ≥ 0.
The feasible region determined by the system of constraints, x + y ≤ 30000, y ≤ 12000, x ≥ 6000, x ≥ y , x ≥ 0 and y ≥ 0 are as follows:
The corner points of the feasible region are D(6000, 0), A3000, 0, F18000, 12000 and E12000, 12000.
The values of Z at these corner points are as follows:
| Corner point | Z = 7x + 10y |
| D(6000, 0) | 7 × 6000 + 10 × 0 = 42000 |
| A3000, 0 | 7× 3000 + 10 × 0 = 21000 |
| F18000, 12000 | 7 × 18000 + 10 × 12000 = 246000 |
| E12000, 12000 | 7 × 12000 + 10 ×12000 = 204000 |
We see that the maximum value of the objective function Z is 246000 which is at F18000, 12000 that means at x = 18000 and y = 12000.
Thus, the optimal value of Z is 246000.
Q10.
Answer :
First, we will convert the given inequations into equations, we obtain the following equations:
x + y = 8, x + 4y = 12, x = 3, y = 2
Region represented by x + y ≥ 8:
The line x + y = 8 meets the coordinate axes at A(8, 0) and B(0, 8) respectively. By joining these points we obtain the line x + y = 8.
Clearly (0,0) does not satisfies the inequation x + y ≥ 8. So,the region in xy plane which does not contain the origin represents the solution set of the inequation x + y ≥ 8.
Region represented by x + 4y ≥ 12:
The line x + 4y = 12 meets the coordinate axes at C(12, 0) and D(0, 3) respectively. By joining these points we obtain the line x + 4y = 12.
Clearly (0,0) satisfies the inequation x + 4y ≥ 12. So,the region in xy plane which contain the origin represents the solution set of the inequation x + 4y ≥ 12.
The line x = 3 is the line that passes through the point (3, 0) and is parallel to Y axis.x ≥ 3 is the region to the right of the line x = 3.
The line y = 2 is the line that passes through the point (0, 12) and is parallel to X axis.y ≥ 2 is the region above the line y = 2.
The corner points of the feasible region are E(3, 5) and F(6, 2).
The values of Z at these corner points are as follows.
| Corner point | Z = 2x + 4y |
| E(3, 5) | 2 × 3 + 4 × 5 = 26 |
| F(6, 2) | 2 × 6 + 4 × 2 = 20 |
Therefore, the minimum value of Z is 20 at the point F(6, 2). Hence, x = 6 and y =2 is the optimal solution of the given LPP.
Thus, the optimal value of Z is 20.
Q11.
Answer :
First, we will convert the given inequations into equations, we obtain the following equations:
2x + y = 10, x + 3y = 15, x = 10, y = 8
Region represented by 2x + y ≥ 10:
The line 2x + y = 10 meets the coordinate axes at A(5, 0) and B(0, 10) respectively. By joining these points we obtain the line 2x + y = 10.
Clearly (0,0) does not satisfies the inequation 2x + y ≥ 10. So,the region in xy plane which does not contain the origin represents the solution set of the inequation 2x + y ≥ 10.
Region represented by x + 3y ≥ 15:
The line x + 3y = 15 meets the coordinate axes at C(15, 0) and D(0, 5) respectively. By joining these points we obtain the line x + 3y = 15.
Clearly (0,0) satisfies the inequation x + 3y ≥ 15. o,the region in xy plane which does not contain the origin represents the solution set of the inequation x + 3y ≥ 15.
The line x = 10 is the line that passes through the point (10, 0) and is parallel to Y axis.x ≤ 10 is the region to the left of the line x = 10.
The line y = 8 is the line that passes through the point (0, 8) and is parallel to X axis.y ≤ 8 is the region below the line y = 8.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0 and y ≥ 0.
The feasible region determined by the system of constraints, 2x + y ≥ 10, x + 3y ≥ 15, x ≤ 10, y ≤ 8, x ≥ 0 and y ≥ 0 are as follows.
The corner points of the feasible region are E(3, 4),H10,53, F(10, 8) and G(1, 8).
The values of Z at these corner points are as follows.
| Corner point | Z = 5x + 3y |
| E(3, 4) | 5 × 3 + 3 × 4 = 27 |
| H10,53 | 5 × 10 + 3× 53= 55 |
| F(10, 8) | 5 × 10 + 3 × 8 = 74 |
| G(1, 8) | 5 × 1 + 3 × 8 = 29 |
Therefore, the minimum value of Z is 27 at the point F(3, 4). Hence, x = 3 and y =4 is the optimal solution of the given LPP.
Thus, the optimal value of Z is 27.
Q12.
Answer :
First, we will convert the given inequations into equations, we obtain the following equations:
x + y = 8, x + 4y = 12, x = 0 and y = 0
5x + 8y = 20 is already an equation.
Region represented by x + y ≤ 8:
The line x + y = 8 meets the coordinate axes at A(8, 0) and B(0, 8) respectively. By joining these points we obtain the line x + y = 8.Clearly (0,0) satisfies the inequation x + y ≤ 8. So,the region in xy plane which contain the origin represents the solution set of the inequation x + y ≤ 8.
Region represented by x + 4y ≥ 12:
The line x + 4y = 12 meets the coordinate axes at C(12, 0) and D(0, 3) respectively. By joining these points we obtain the line x + 4y = 12.Clearly (0,0) satisfies the inequation x + 4y ≥ 12. So,the region in xy plane which does not contain the origin represents the solution set of the inequation x + 4y ≥ 12.
The line 5x + 8y = 20 is the line that passes through E(4, 0) and F0, 52 .
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0 and y ≥ 0.
The feasible region determined by the system of constraints, x + y ≤ 8, x + 4y ≥ 12, 5x + 8y = 20, x ≥ 0 and y ≥ 0 are as follows.
The corner points of the feasible region are B(0,8), D(0,3), G203, 43.
The values of Z at these corner points are as follows.
| Corner point | Z = 30x + 20y |
| B(0,8) | 160 |
| D(0,3) | 60 |
| G203, 43 | 266.66 |
Therefore, the minimum value of Z is 60 at the point D(0,3). Hence, x = 0 and y =3 is the optimal solution of the given LPP.
Thus, the optimal value of Z is 60.
Q13.
Answer :
We need to maximize Z = 4x + 3y
First, we will convert the given inequations into equations, we obtain the following equations:
3x + 4y = 24, 8x + 6y = 48, x = 5 , y = 6, x = 0 and y = 0.
The line 3x + 4y = 24 meets the coordinate axis at A(8, 0) and B(0,6). Join these points to obtain the line 3x + 4y = 24.
Clearly, (0, 0) satisfies the inequation 3x + 4y ≤ 24.So, the region in xy-plane that contains the origin represents the solution set of the given equation.
The line 8x + 6y = 48 meets the coordinate axis at C(6, 0) and D(0,8). Join these points to obtain the line 8x + 6y = 48.
Clearly, (0, 0) satisfies the inequation 8x + 6y ≤ 48. So, the region in xy-plane that contains the origin represents the solution set of the given equation.
x = 5 is the line passing through x = 5 parallel to the Y axis.
y = 6 is the line passing through y = 6 parallel to the X axis.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations.
These lines are drawn using a suitable scale.
The corner points of the feasible region are O(0, 0), G5, 0, F5,43, E247,247 and B0, 6.
The values of Z at these corner points are as follows.
| Corner point | Z = 4x + 3y |
| O(0, 0) | 4× 0 + 3 × 0 = 0 |
| G5, 0 | 4 × 5 + 3 × 0 = 20 |
| F5,43 | 4 × 5 + 3 × 43= 24 |
| E247,247 | 4 × 247+ 3 × 247= 1967= 24 |
| B0, 6 | 4 × 0 + 3 × 6 = 18 |
We see that the maximum value of the objective function Z is 24 which is at F5,43 and E247,247.
Thus, the optimal value of Z is 24.
Q14.
Answer :
First, we will convert the given inequations into equations, we obtain the following equations:
x − y = 0, − x + 2y = 2, x = 3, y = 4, x = 0 and y = 0.
Region represented by x − y ≥ 0 or x ≥ y:
The line x − y = 0 or x = y passes through the origin.The region to the right of the line x = y will satisfy the given inequation.
Let’s check by taking an example like if we take a point (4, 3) to the right of the line x = y .Here x ≥ y.So, it satisfy the given inequation. Take a point (4, 5) to the left of the line x = y. Here, x ≤ y. That means it does not satisfy the given inequation.
Region represented by − x + 2y ≥ 2:
The line − x + 2y = 2 meets the coordinate axes at A(−2, 0) and B(0, 1) respectively. By joining these points we obtain the line
− x + 2y = 2.Clearly (0,0) does not satisfies the inequation − x + 2y ≥ 2. So,the region in xy plane which does not contain the origin represents the solution set of the inequation − x + 2y ≥ 2 .
The line x = 3 is the line that passes through the point (3, 0) and is parallel to Y axis. x ≥ 3 is the region to the right of the line x = 3.
The line y = 4 is the line that passes through the point (0, 4) and is parallel to X axis. y ≤ 4 is the region below the line y = 4.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0 and y ≥ 0.
The feasible region determined by the system of constraints x − y ≥ 0,− x + 2y ≥ 2, x ≥ 3, y ≤ 4, x ≥ 0 and y ≥ 0 are as follows.
The corner points of the feasible region are C3, 52,D3, 3, E(4, 4) and F(6, 4).
The values of Z at these corner points are as follows.
| Corner point | Z = x − 5y + 20 |
| C3, 52 | 3 − 5 × 52+ 20 = 212 |
| D3, 3 | 3 − 5 × 3 + 20 = 8 |
| E(4, 4) | 4 − 5 × 4 + 20 = 4 |
| F(6, 4) | 6 − 5 × 4 + 20 = 6 |
Therefore, the minimum value of Z is 4 at the point E(4, 4). Hence, x = 4 and y = 4 is the optimal solution of the given LPP.
Thus, the optimal value of Z is 4.
Q15.
Answer :
We need to maximize Z = 3x + 5y
First, we will convert the given inequations into equations, we obtain the following equations:
x + 2y = 20, x + y = 15, y = 5 , x = 0 and y = 0.
The line x + 2y = 20 meets the coordinate axis at A(20, 0) and B(0,10). Join these points to obtain the line x + 2y = 20.
Clearly, (0, 0) satisfies the inequation x + 2y ≤ 20. So, the region in xy-plane that contains the origin represents the solution set of the given equation.
The line x + y = 15 meets the coordinate axis at C(15, 0) and D(0,15). Join these points to obtain the line x + y = 15.
Clearly, (0, 0) satisfies the inequation x + y ≤ 15. So, the region in xy-plane that contains the origin represents the solution set of the given equation.
y = 5 is the line passing through (0, 5) and parallel to the X axis.The region below the line y = 5 will satisfy the given inequation.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations.
These lines are drawn using a suitable scale.
The corner points of the feasible region are O(0, 0), C15, 0, E10, 5 and F0, 5
The values of Z at these corner points are as follows.
| Corner point | Z = 3x + 5y |
| O(0, 0) | 3 × 0 + 5 × 0 = 0 |
| C15, 0 | 3 × 15 + 5 × 0 = 45 |
| E10, 5 | 3 × 10 + 5 × 5 = 55 |
| F0, 5 | 3 × 0 + 5 × 5 = 25 |
We see that the maximum value of the objective function Z is 55 which is at E10, 5.
Thus, the optimal value of Z is 55.
Q16.
Answer :
First, we will convert the given inequations into equations, we obtain the following equations:
x1 + 3×2 = 3, x1 + x2 = 2, x1 = 0 and x2 = 0
Region represented by x1 + 3×2 ≥ 3 :
The line x1 + 3×2 = 3 meets the coordinate axes at A(3, 0) and B(0, 1) respectively. By joining these points we obtain the line x1 + 3×2 = 3.
Clearly (0,0) does not satisfies the inequation x1 + 3×2 ≥ 3 .So,the region in the plane which does not contain the origin represents the solution set of the inequation x1 + 3×2 ≥ 3.
Region represented by x1 + x2 ≥ 2:
The line x1 + x2 = 2 meets the coordinate axes at C(2, 0) and D(0, 2) respectively. By joining these points we obtain the line x1 + x2 = 2.Clearly (0,0) does not satisfies the inequation x1 + x2 ≥ 2. So,the region containing the origin represents the solution set of the inequation x1 + x2 ≥ 2.
Region represented by x1 ≥ 0 and x2 ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x1 ≥ 0 and x2 ≥ 0.
The feasible region determined by the system of constraints, x1 + 3×2 ≥ 3 , x1 + x2 ≥ 2, x1 ≥ 0, and x2 ≥ 0, are as follows.
The corner points of the feasible region are O(0, 0), B(0, 1), E32, 12 and C(2, 0).
The values of Z at these corner points are as follows.
| Corner point | Z = 3x1 + 5x2 |
| O(0, 0) | 3 × 0 + 5 × 0 = 0 |
| B(0, 1) | 3 × 0 + 5 × 1 = 5 |
| E32, 12 | 3 × 32+ 5 ×12= 7 |
| C(2, 0) | 3 × 2 + 5 × 0 = 6 |
Therefore, the minimum value of Z is 0 at the point O(0, 0). Hence, x1 = 0 and x2 = 0 is the optimal solution of the given LPP.
Thus, the optimal value of Z is 0.
Page 30.33 Ex.30.2
Q17.
Answer :
First, we will convert the given inequations into equations, we obtain the following equations:
x + y = 1, 10x +y = 5, x + 10y = 1, x = 0 and y = 0
Region represented by x + y ≥ 1:
The line x + y = 1 meets the coordinate axes at A(1, 0) and B(0,1) respectively. By joining these points we obtain the line x + y = 1.
Clearly (0,0) does not satisfies the inequation x + y ≥ 1. So,the region in xy plane which does not contain the origin represents the solution set of the inequation x + y ≥ 1.
Region represented by 10x +y ≥ 5:
The line 10x +y = 5 meets the coordinate axes at C12, 0 and D(0, 5) respectively. By joining these points we obtain the line
10x +y = 5.Clearly (0,0) does not satisfies the inequation 10x +y ≥ 5. So,the region which does not contains the origin represents the solution set of the inequation 10x +y ≥ 5.
Region represented by x + 10y ≥ 1:
The line x + 10y = 1 meets the coordinate axes at A1, 0 and F0, 110 respectively. By joining these points we obtain the line
x + 10y = 1.Clearly (0,0) does not satisfies the inequation x + 10y ≥ 1. So,the region which does not contains the origin represents the solution set of the inequation x + 10y ≥ 1.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints x + y ≥ 1, 10x +y ≥ 5, x + 10y ≥ 1, x ≥ 0, and y ≥ 0, are as follows.
The feasible region is unbounded.Therefore, the maximum value is infinity i.e. the solution is unbounded.
Disclaimer:
The obtained answer is for the given question. Answer in the book is 2.It would be 2 if the question is to minimize Z instead of to maximize Z.
Q18.
Answer :
First, we will convert the given inequations into equations, we obtain the following equations:
−x1 + 3×2 = 10, x1 + x2 = 6, x1 + x2 = 2, x1 = 0 and x2 = 0
Region represented by −x1 + 3×2 ≤ 10:
The line −x1 + 3×2 = 10 meets the coordinate axes at A(−10, 0) and B0, 103 respectively. By joining these points we obtain the line −x1 + 3×2 = 10.
Clearly (0,0) satisfies the inequation −x1 + 3×2 ≤ 10 .So,the region in the plane which contain the origin represents the solution set of the inequation
−x1 + 3×2 ≤ 10.
Region represented by x1 + x2 ≤ 6:
The line x1 + x2 = 6 meets the coordinate axes at C(6, 0) and D(0, 6) respectively. By joining these points we obtain the line x1 + x2 = 6.Clearly (0,0) satisfies the inequation x1 + x2 ≤ 6. So,the region containing the origin represents the solution set of the inequation x1 + x2 ≤ 6.
Region represented by x1− x2 ≤ 2:
The line x1 − x2 = 2 meets the coordinate axes at E(2, 0) and F(0, −2) respectively. By joining these points we obtain the line x1 − x2 = 2.Clearly (0,0) satisfies the inequation x1− x2 ≤ 2. So,the region containing the origin represents the solution set of the inequation x1− x2 ≤ 2.
Region represented by x1 ≥ 0 and x2 ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x1 ≥ 0 and x2 ≥ 0.
The feasible region determined by the system of constraints, −x1 + 3×2 ≤ 10, x1 + x2 ≤ 6, x1− x2 ≤ 2, x1 ≥ 0, and x2 ≥ 0, are as follows.
The corner points of the feasible region are O(0, 0), E(2, 0), H(4, 2), G(2, 4) and B0, 103.
The values of Z at these corner points are as follows.
| Corner point | Z = −x1 + 2x2 |
| O(0, 0) | −1 × 0 + 2 × 0 = 0 |
| E(2, 0) | −1 × 2 + 2 × 0 = −2 |
| H(4, 2) | −1 × 4 + 2 × 2 = 0 |
| G(2, 4) | −1 × 2 + 2 × 4 = 6 |
| B0, 103 | −1 × 0 + 2 × 103= 03 |
We see that the maximum value of the objective function Z is 203 which is at B0, 103.
Q19.
Answer :
We need to maximize Z = x + y
First, we will convert the given inequations into equations, we obtain the following equations:
−2x + y = 1, x = 2, x + y = 3, x = 0 and y = 0.
The line −2x + y = 1 meets the coordinate axis at A-12, 0 and B(0, 1). Join these points to obtain the line −2x + y = 1 .
Clearly, (0, 0) satisfies the inequation −2x + y ≤ 1. So, the region in xy-plane that contains the origin represents the solution set of the given equation.
x = 2 is the line passing through (2, 0) and parallel to the Y axis.The region below the line x = 2 will satisfy the given inequation.
The line x + y = 3 meets the coordinate axis at C(3, 0) and D(0, 3). Join these points to obtain the line x + y = 3.
Clearly, (0, 0) satisfies the inequation x + y ≤ 3. So, the region in xy-plane that contains the origin represents the solution set of the given equation.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations.
These lines are drawn using a suitable scale.
The corner points of the feasible region are O(0, 0),G2, 0, E2, 1 and F23, 73
The values of Z at these corner points are as follows.
| Corner point | Z = x + y |
| O(0, 0) | 0 + 0 = 0 |
| C2, 0 | 2 + 0 = 2 |
| E2, 1 | 2 +1 = 3 |
| F23, 73 | 23+73=93=3 |
We see that the maximum value of the objective function Z is 3 which is at E2, 1 and F23, 73.
Thus, the optimal value of Z is 3.
Q20.
Answer :
First, we will convert the given inequations into equations, we obtain the following equations:
x1 − x2 = −1, −x1 + x2 = 0, x1 = 0 and x2 = 0
Region represented by x1 − x2 ≤ −1:
The line x1 − x2 = −1 meets the coordinate axes at A(−1, 0) and B(0, 1) respectively. By joining these points we obtain the line x1 − x2 = −1.
Clearly (0,0) does not satisfies the inequation x1 − x2 ≤ −1 .So,the region in the plane which does not contain the origin represents the solution set of the inequation x1 − x2 ≤ −1.
Region represented by −x1 + x2 ≤ 0 or x1 ≥ x2:
The line −x1 + x2 = 0 or x1 = x2 is the line passing through (0, 0).The region to the right of the line x1 = x2 will satisfy the given inequation −x1 + x2 ≤ 0.
If we take a point (1, 3) to the left of the line x1 = x2. Here, 1≤3 which is not satifying the inequation x1 ≥ x2. Therefore, region to the right of the line x1 = x2 will satisfy the given inequation −x1 + x2 ≤ 0.
Region represented by x1 ≥ 0 and x2 ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x1 ≥ 0 and x2 ≥ 0.
The feasible region determined by the system of constraints, x1 − x2 ≤ −1, −x1 + x2 ≤ 0, x1 ≥ 0, and x2 ≥ 0, are as follows.
We observe that the feasible region of the given LPP does not exist.
Q21.
Answer :
First, we will convert the given inequations into equations, we obtain the following equations:
x − y = 1, x + y = 3, x = 0 and y = 0
Region represented by x − y ≤ 1:
The line x − y = 1 meets the coordinate axes at A(1, 0) and B(0, −1) respectively. By joining these points we obtain the line x − y = 1.
Clearly (0,0) satisfies the inequation x + y ≤ 8. So,the region in xy plane which contain the origin represents the solution set of the inequation x − y ≤ 1.
Region represented by x + y ≥ 3:
The line x + y = 3 meets the coordinate axes at C(3, 0) and D(0, 3) respectively. By joining these points we obtain the line x + y = 3.
Clearly (0,0) satisfies the inequation x + y ≥ 3. So,the region in xy plane which does not contain the origin represents the solution set of the inequation x + y ≥ 3.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0 and y ≥ 0.
The feasible region determined by the system of constraints x − y ≤ 1, x + y ≥ 3, x ≥ 0 and y ≥ 0 are as follows.
The feasible region is unbounded.We would obtain the maximum value at infinity.
Therefore,maximum value will be infinity i.e. the solution is unboundedm
Q22.
Answer :
First, we will convert the given inequations into equations, we obtain the following equations:
5x + y = 10, x +y = 6, x + 4y = 12, x = 0 and y = 0
Region represented by 5x + y ≥ 10:
The line 5x + y = 10 meets the coordinate axes at A(2, 0) and B(0, 10) respectively. By joining these points we obtain the line 5x + y = 10.
Clearly (0,0) does not satisfies the inequation 5x + y ≥ 10. So,the region in xy plane which does not contain the origin represents the solution set of the inequation 5x + y ≥ 10.
Region represented by x +y ≥ 6:
The line x +y = 6 meets the coordinate axes at C(6,0) and D(0, 6) respectively. By joining these points we obtain the line
2x +3y = 30.Clearly (0,0) does not satisfies the inequation x +y ≥ 6. So,the region which does not contain the origin represents the solution set of the inequation 2x +3y ≥ 30.
Region represented by x + 4y ≥ 12
The line x + 4y = 12 meets the coordinate axes at E(12, 0) and F(0, 3) respectively. By joining these points we obtain the line
x + 4y = 12.Clearly (0,0) does not satisfies the inequation x + 4y ≥ 12. So,the region which does not contain the origin represents the solution set of the inequation x + 4y ≥ 12.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints 5x + y ≥ 10, x +y ≥ 6,x + 4y ≥ 12, x ≥ 0, and y ≥ 0, are as follows.
The corner points of the feasible region are B(0, 10), G(1,5), H(4,2) and E(12,0).
The values of Z at these corner points are as follows
| Corner point | Z = 3x + 2y |
| B(0, 10) | 3 × 0 + 3 × 10 = 30 |
| G(1,5) | 3 × 1 + 2 × 5 = 13 |
| H(4,2) | 3 × 4 + 2 × 2 = 16 |
| E(12,0) | 3 × 12 + 2 × 0 = 36 |
Therefore, the minimum value of Z is 13 at the point G(1,5). Hence, x = 1 and y = 5 is the optimal solution of the given LPP.
Thus, the optimal value of Z is 13.
Q23.
Answer :
First, we will convert the given inequations into equations, we obtain the following equations:
x + y = 4, x + y = 3, x − 2y = 2, x = 0 and y = 0.
The line x + 3y = 6 meets the coordinate axis at A6, 0 and B(0, 2). Join these points to obtain the line x + 3y = 6.
Clearly, (0, 0) does not satisfies the inequation x + 3y ≥ 6. So, the region in xy-plane that does not contains the origin represents the solution set of the given equation.
The line x − 3y = 3 meets the coordinate axis at C(3, 0) and D(0, −1). Join these points to obtain the line x − 3y = 3.
Clearly, (0, 0) satisfies the inequation x − 3y ≤ 3. So, the region in xy-plane that contains the origin represents the solution set of the given equation.
The line 3x + 4y = 24 meets the coordinate axis at E(8, 0) and F(0, 6). Join these points to obtain the line 3x + 4y = 24.
Clearly, (0, 0) satisfies the inequation 3x + 4y ≤ 24. So, the region in xy-plane that contains the origin represents the solution set of the given equation.
The line −3x + 2y = 6 meets the coordinate axis at G(−2, 0) and H(0, 3). Join these points to obtain the line −3x + 2y = 6.
Clearly, (0, 0) satisfies the inequation −3x + 2y ≤ 6. So, the region in xy-plane that contains the origin represents the solution set of the given equation.
The line 5x + y = 5 meets the coordinate axis at I1, 0 and J(0, 5). Join these points to obtain the line 5x + y = 5.
Clearly, (0, 0) does not satisfies the inequation 5x + y ≥ 5. So, the region in xy-plane that does not contains the origin represents the solution set of the given equation.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations.
These lines are drawn using a suitable scale.
The corner points of the feasible region are P413,4513 , K43, 5 , L8413,1513 , M92,12 , N914,2514
The values of Z at these corner points are as follows.
| Corner point | Z = 2x + y |
| P 413,4513 | 2 × 413+ 4513= 5313 |
| K 43, 5 | 2 × 43+ 5 = 233 |
| L 8413,1513 | 2 × 8413+ 1513= 18313 |
| M 92,12 | 2 × 92+ 12= 192 |
| N 914,2514 | 2 × 914+ 2514= 4314 |
We see that the minimum value of the objective function Z is 4314 which is at N914,2514 and maximum value of the objective function is 18313 which is at L8413,1513 .
Q24.
Answer :
First, we will convert the given inequations into equations, we obtain the following equations:
−2x + y = 4, x + y = 3, x − 2y = 2, x = 0 and y = 0.
The line −2x + y = 4 meets the coordinate axis at A-2, 0 and B(0, 4). Join these points to obtain the line −2x + y = 4.
Clearly, (0, 0) satisfies the inequation −2x + y ≤ 4. So, the region in xy-plane that contains the origin represents the solution set of the given equation.
The line x + y = 3 meets the coordinate axis at C(3, 0) and D(0, 3). Join these points to obtain the line x + y = 3.
Clearly, (0, 0) does not satisfies the inequation x + y ≥ 3. So, the region in xy-plane that does not contains the origin represents the solution set of the given equation.
The line x − 2y = 2 meets the coordinate axis at E(2, 0) and F(0, −1). Join these points to obtain the line x − 2y = 2.
Clearly, (0, 0) satisfies the inequation x − 2y ≤ 2. So, the region in xy-plane that contains the origin represents the solution set of the given equation.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations.
These lines are drawn using a suitable scale.
The corner points of the feasible region are B0, 4, D0, 3 and G83, 13
The values of Z at these corner points are as follows.
| Corner point | Z = 3x + 5y |
| B0, 4 | 3 × 0+ 5 × 4 = 20 |
| D0, 3 | 3 × 0+ 5 × 3 = 15 |
| G83, 13 | 3 × 83+ 5 × 13= 293 |
We see that the minimum value of the objective function Z is 293 which is at G83, 13.
Thus, the optimal value of Z is 293.
Q25.
Answer :
We have to maximize Z = 60x + 15y
First, we will convert the given inequations into equations, we obtain the following equations:
x + y = 50, 3x + y = 90, x = 0 and y = 0
Region represented by x + y ≤ 50:
The line x + y = 50 meets the coordinate axes at A(50,0) and B(0,50) respectively. By joining these points we obtain the line 3x + 5y = 15.
Clearly (0,0) satisfies the inequation x + y ≤ 50. So,the region containing the origin represents the solution set of the inequation x + y ≤ 50.
Region represented by 3x + y ≤ 90:
The line 3x + y = 90 meets the coordinate axes at C(30, 0) and D(0, 90) respectively. By joining these points we obtain the line 3x + y = 90.
Clearly (0,0) satisfies the inequation 3x + y ≤ 90. So,the region containing the origin represents the solution set of the inequation 3x + y ≤ 90.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints, x + y ≤ 50, 3x + y ≤ 90, x ≥ 0, and y ≥ 0, are as follows.
The corner points of the feasible region are O(0, 0), C(30, 0), E20, 30 and B(0, 50).
The values of Z at these corner points are as follows.
| Corner point | Z = 60x + 15y |
| O(0, 0) | 60 × 0 + 15 × 0 = 0 |
| C(30, 0) | 60 × 30 + 15 × 0 = 1800 |
| E20, 30 | 60 × 20 + 15 × 30 =1650 |
| B(0, 50) | 60 × 0 + 15 × 50 = 50 |
Therefore, the maximum value of Z is 1800 at the point 30, 0.Hence, x = 30 and y = 0 is the optimal solution of the given LPP.
Thus, the optimal value of Z is 1800.
Page 30.49 Ex.30.3
Q1.
Answer :
Let 25x grams of food F1 and 25y grams of food F2 be used to fulfil the minimum requirement of thiamine, phosphorus and iron.
As, we are given
| Nutrients | Food | F1 | F2 |
| Thiamine | 0.25 | 0.10 | |
| Phosphorous | 0.75 | 1.50 | |
And the minimum requirement of the nutrients in the diet are 1.00 mg of thiamine, 7.50 mg of phosphorous and 10.00 mg of iron.
Therefore, 0.25x+0.10y≥10.75x+1.50y ≥7.51.6x + 0.8y ≥ 10Since, the quantity cannot be negative∴ x, y≥0
The cost of F1 is 20 paise per 25 gms while the cost of F2 is 15 paise per 25 gms.Therefore, the cost of 25x grams of food F1 and 25y grams of food F2 is
Rs (0.20x + 0.15y).
Hence,
Minimize Z = 0.20x+0.15y
subject to
0.25x+0.10y≥10.75x+1.50y ≥7.51.6x + 0.8y ≥ 10 x, y≥0
First, we will convert the given inequations into equations, we obtain the following equations:
0.25x + 0.10y = 1, 0.75x + 1.50y = 7.5, 1.6x + 0.8y = 10, x = 0 and y = 0.
The line 0.25x + 0.10y = 1 meets the coordinate axis at A4, 0 and B(0, 10). Join these points to obtain the line 0.25x + 0.10y = 1.
Clearly, (0, 0) does not satisfies the inequation 0.25x + 0.10y ≥ 1. So, the region in xy-plane that does not contains the origin represents the solution set of the given equation.
The line 0.75x + 1.50y = 7.5. meets the coordinate axis at C(10, 0) and D(0, 5). Join these points to obtain the line 0.75x + 1.50y = 7.5.
Clearly, (0, 0) does not satisfies the inequation 0.75x + 1.50y ≥ 0.75. So, the region in xy-plane that does not contains the origin represents the solution set of the given equation.
The line 1.6x + 0.8y = 10 meets the coordinate axis at E254, 0 and F0, 252. Join these points to obtain the line 1.6x + 0.8y = 10.
Clearly, (0, 0) does not satisfies the inequation 1.6x + 0.8y ≥ 10. So, the region in xy-plane that does not contains the origin represents the solution set of the given equation.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations.
These lines are drawn using a suitable scale.
The corner points of the feasible region are F(0, 12.5), G(5, 2.5), C(10, 0)
The value of the objective function at these points are given by the following table
| Points | Value of Z |
| F | 0.20(0)+0.15(12.5) = 1.875 |
| G | 0.20(5)+0.15(2.5) = 1.375 |
| C | 0.20(10) + 0.15(0) = 200 |
Thus, the minimum cost is at G which is Rs 1.375
Page 30.50 Ex.30.3
Q2.
Answer :
Let the sick person takes x units and y units of food I and II respectively that were taken in the diet.
Since, per unit of food I costs Rs 4 and that of food II costs Rs 3.
Therefore, x units of food I costs Rs 4x and y units of food II costs Rs 3y.
Total cost = Rs (4x + 3y)
Let Z denote the total cost
Then, Z = 4x + 3y
If one unit of A contains 200 units of vitamin and one unit of food B contains 100 units of vitamin.
Thus, x units of food I and y units of food II contains 200x + 100y units of vitamin.
But a diet for a sick person must contain at least 4000 units of vitamins.
∴ 200x+100y≥4000
If one unit of A contains 1 unit of mineral and one unit of food B contains 2 units of mineral.
Thus, x units of food I and y units of food II contains x + 2y units of mineral.
But a diet for a sick person must contain at least 50 units of vitamins.
∴ x+2y ≥ 50
If one unit of A contains 40 calories and one unit of food B contains 40 calories.
Thus, x units of food I and y units of food II contains 40x + 40y units of calories.
But a diet for a sick person must contain at least 1400 calories.
∴40x+40y≥1400
Finally, the quantities of food I and food II are non negative values.
So, x, y ≥ 0
Hence, the required LPP is as follows:
Min Z = 4x + 3y
subject to
200x+100y≥4000x+2y ≥5040x + 40y ≥ 1400x, y≥0
First, we will convert the given inequations into equations, we obtain the following equations:
200x + 100y = 4000, x +2y = 50, 40x + 40y =1400, x = 0 and y = 0
Region represented by 200x + 100y ≥ 4000:
The line 200x + 100y = 4000 meets the coordinate axes at A1(20, 0) and B1(0,40) respectively. By joining these points we obtain the line
200x + 100y = 4000.Clearly (0,0) does not satisfies the inequation 200x + 100y ≥ 4000. So,the region in xy plane which does not contain the origin represents the solution set of the inequation 200x + 100y ≥ 4000.
Region represented by x +2y ≥ 50:
The line x +2y = 50 meets the coordinate axes at C1(50, 0) and D1(0, 25) respectively. By joining these points we obtain the line
x +2y = 50.Clearly (0,0) does not satisfies the x +2y ≥ 50. So,the region which does not contains the origin represents the solution set of the inequation x +2y ≥ 50.
Region represented by 40x + 40y ≥ 1400:
The line 40x + 40y = 1400 meets the coordinate axes at E1(35, 0) and F1(0, 35) respectively. By joining these points we obtain the line
40x + 40y = 1400.Clearly (0,0) does not satisfies the inequation 40x + 40y ≥ 1400. So,the region which does not contains the origin represents the solution set of the inequation 40x + 40y ≥ 1400.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints 200x + 100y ≥ 4000,x +2y ≥ 50, 40x + 40y ≥ 1400, x ≥ 0, and y ≥ 0 are as follows.
The corner points of the feasible region are B1(0, 40), G1(5, 30), H1(20, 15) and C1(50, 0)
The value of the objective function at these points are given by the following table
| Points | Value of Z |
| B1 | 4(0)+3(40) = 120 |
| G1 | 4(5)+3(30) = 110 |
| H1 | 4(20) + 3(15) = 125 |
| C1 | 4(50)+3(0) = 200 |
The minimum cost is Rs 110 which is at G1(5, 30).
Hence, the required combination of food is 5 units of food A and 30 units of food B.
Q3.
Answer :
Let the person takes x units and y units of food I and II respectively that were taken in the diet.
Since, per unit of food I costs Re 0.60 and that of food II costs Re 1.00.
Therefore, x lbs of food I costs Rs 0.60x and y lbs of food II costs Rs 1.00y.
Total cost per day = Rs (0.60x +1.00y)
Let Z denote the total cost per day
Then, Z = 0.60x +1.00y
Since, each unit of food I contains 10 units of calcium.Therefore, x units of food I contains 10x units of calcium.
Each unit of food II contains 4 units of calcium.So, y units of food II contains 4y units of calcium.
Thus, x units of food I and y units of food II contains (10x + 4y) units of calcium.
But, the minimum requirement is 20 units of calcium.
∴ 10x+4y≥20
Since, each unit of food I contains 5 units of protein.Therefore, x units of food I contains 5x units of protein.
Each unit of food II contains 6 units of protein.So,y units of food II contains 6y units of protein.
Thus, x units of food I and y units of food II contains (5x + 6y) units of protein.
But, the minimum requirement is 20 lbs of protein.
∴ 5x+6y ≥ 20
Since, each unit of food I contains 2 units of calories.Therefore, x units of food I contains 2x units of calories.
Each unit of food II contains 6 units of calories.So,y units of food II contains 6y units of calories.
Thus, x units of food I and y units of food II contains (2x + 6y) units of calories.
But, the minimum requirement is 12 lbs of calories.
∴2x+6y≥12
Finally, the quantities of food I and food II are non negative values.
So, x, y ≥ 0
Hence, the required LPP is as follows:
Min Z = 0.60x + 1.00y
subject to
10x+4y≥205x+6y≥202x+6y≥12x, y≥0
First, we will convert the given inequations into equations, we obtain the following equations:
10x + 4y = 20, 5x +6y = 20, 2x + 6y =12, x = 0 and y = 0
Region represented by 10x + 4y ≥ 20:
The line 10x + 4y = 20 meets the coordinate axes at A(2, 0) and B(0, 5) respectively. By joining these points we obtain the line
10x + 4y = 20.Clearly (0,0) does not satisfies the inequation 10x + 4y ≥ 20. So,the region in xy plane which does not contain the origin represents the solution set of the inequation 10x + 4y ≥ 20.
Region represented by 5x +6y ≥ 20:
The line 5x +6y = 20 meets the coordinate axes at C4, 0 and D0, 103 respectively. By joining these points we obtain the line
5x +6y = 20.Clearly (0,0) does not satisfies the 5x +6y ≥ 20. So,the region which does not contains the origin represents the solution set of the inequation 5x +6y ≥ 20.
Region represented by 2x + 6y ≥ 12:
The line 2x + 6y =12 meets the coordinate axes at E6, 0 and F0, 2 respectively. By joining these points we obtain the line
2x + 6y =12.Clearly (0,0) does not satisfies the inequation 2x + 6y ≥ 12. So,the region which does not contains the origin represents the solution set of the inequation 2x + 6y ≥ 12.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints 10x + 4y ≥ 20, 5x +6y ≥ 20, 2x + 6y ≥ 12, x ≥ 0, and y ≥ 0 are as follows.
The set of all feasible solutions of the above LPP is represented by the feasible region shaded in the graph.
The corner points of the feasible region are B(0, 5), G1,52, H83,109 and E6, 0
The value of the objective function at these points are given by the following table
| Points | Value of Z |
| B | 0.60+5=5 |
| G | 0.61+52=3.1 |
| H | 0.683+109=1.6+1.1=2.7 |
| E | 0.66+0=3.6 |
We see that the minimum cost is 2.7 which is at 83,109.
Thus, at minimum cost, 83 units of food I and 109 units of food II should be included in the diet.
Q4.
Answer :
Let the dietician wishes to mix x units of food A and y units of food B.
Therefore, x,y≥0
The given information can be tabulated as follows
| Thiamine(mg) | Calories | |
| Food A | 0.12 | 100 |
| Food B | 0.1 | 150 |
| Minimum requirement | 0.5 | 600 |
According to the question,
The constraints are
0.12x+0.1y≥0.5100x+150y≥600
It is given that each food costs 10 paise per units
Therefore,
Total cost, Z = 10x+10y
Thus, the mathematical formulation of the given linear programmimg problem is
0.12x+0.1y≥0.5100x+150y≥600
Region represented by 0.12x +0.1y ≥ 0.5:
The line 0.12x + 0.6y = 20 meets the coordinate axes at A1256, 0 and B10, 5 respectively. By joining these points we obtain the line
0.12x + 0.6y = 20.Clearly (0,0) does not satisfies the 0.12x + 0.6y = 20. So,the region which does not contains the origin represents the solution set of the inequation 0.12x +0.1y ≥ 0.5.
Region represented by 100x + 150y ≥ 600:
The line 100x + 150y = 600 meets the coordinate axes at C16, 0 and D10, 4 respectively. By joining these points we obtain the line 100x + 150y = 600. Clearly (0,0) does not satisfies the inequation 100x + 150y ≥ 600. So,the region which does not contains the origin represents the solution set of the inequation 100x + 150y ≥ 600.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints 0.12x +0.1y ≥ 0.5, 100x + 150y ≥ 600, x ≥ 0, and y ≥ 0 are as follows.
The corner points are B1(0, 5), E1158, 114, C16, 0
The values of Z at these corner points are as follows
| Corner point | Z= 10x +10y |
| B1 | 50 |
| E1 | 46.2 |
| C1 | 60 |
The minimum value of Z is at E1158, 114.
Hence, cheapest combination of foods will be 1.875 units of food A and 2.75 units of food B.
Q5.
Answer :
Let the dietician wishes to mix x kg of food X and y kg of food Y.
Therefore, x,y≥0
As we are given,
| Vitamin A | Vitamin B | Vitamin C | Vitamin D | |
| Food X Food Y | 1 2 | 1 1 | 1 3 |
It is given that the mixture should contain at least 6 units of vitamin A, 7 units of vitamin B, 11 units of vitamin C and 9 units of vitamin D.
Therefore, the constraints are
x+2y≥6x+y≥7x+3y≥112x+y≥9
It is given that cost of food X is Rs 5 per kg and cost of food Y is Rs 8 per kg.
Thus, Z = 5x+8y
Thus, the mathematical formulation of the given linear programmimg problem is
Minimize Z = 5x+8y
subject to
x+2y≥6x+y≥7x+3y≥112x+y≥9
First, we will convert the given inequations into equations, we obtain the following equations:
x + 2y = 6, x + y = 7, x + 3y =11, 2x + y =9, x = 0 and y = 0.
The line x + 2y = 6 meets the coordinate axis at A1(6, 0) and B1(0, 3). Join these points to obtain the line x + 2y = 6. Clearly, (0, 0) does not satisfies the inequation x + 2y ≥ 6. So, the region in xy-plane that does not contains the origin represents the solution set of the given equation.
The line x + y = 7 meets the coordinate axis at C1(7, 0) and D1(0, 7). Join these points to obtain the line x + y = 7. Clearly, (0, 0) does not satisfies the inequation x + y ≥ 7. So, the region in xy-plane that does not contains the origin represents the solution set of the given equation.
The line x + 3y = 11 meets the coordinate axis at E111, 0 and F10, 113. Join these points to obtain the line x + 3y = 11.Clearly, (0, 0) does not satisfies the inequation x + 3y ≥ 11. So, the region in xy-plane that does not contains the origin represents the solution set of the given equation.
The line 2x + y = 9 meets the coordinate axis at G192, 0 and H10, 9. Join these points to obtain the line 2x + y = 9.Clearly, (0, 0) does not satisfies the inequation 2x + y ≥ 9. So, the region in xy-plane that does not contains the origin represents the solution set of the given equation.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations.
These lines are drawn using a suitable scale.
The feasible region determined by the system of constraints is
The corner points are H1(0, 9), I1(2 ,5), J1(5, 2), E1(11, 0).
The values of Z at these corner points are as follows
| Corner point | Z= 5x + 8y |
| H1 | 72 |
| I1 | 50 |
| J1 | 41 |
| E1 | 55 |
The minimum value of Z is at J1(5, 2) which is Rs 41.
Hence, cheapest combination of foods will be 5 units of food X and 2 units of food Y.
Q6.
Answer :
Let the dietician wishes to mix x units of food F1 and y units of food F2.
Clearly, x,y≥0
The given information can be tabulated as follows:
| Vitamin A | Minerals | |
| Food F1 | 3 | 4 |
| Food F2 | 6 | 3 |
| Minimum requirement | 80 | 100 |
3x+6y≥804x+3y≥100
It is given that cost of food F1 and F2 is Rs 4 and Rs 6 per unit respectively. Therefore, cost of x units of food F1 and y units of food F2 is Rs 4x and Rs 6y respectively.
Let Z denote the total cost
∴ Z = 4x + 6y
Thus, the mathematical formulation of the given linear programmimg problem is
Minimize Z = 4x+6y subject to
3x+6y≥804x+3y≥100
x,y≥0
First, we will convert the given inequations into equations, we obtain the following equations:
3x + 6y = 80, 4x + 3y = 100, x = 0 and y = 0
The line 3x + 6y = 80 meets the coordinate axis at A803, 0 and B0, 403. Join these points to obtain the line 3x + 6y = 80. Clearly, (0, 0) does not satisfies the inequation 3x + 6y ≥ 80. So, the region in xy-plane that does not contains the origin represents the solution set of the given equation.
The line 4x + 3y = 100 meets the coordinate axis at C(25, 0) and D0, 1003. Join these points to obtain the line 4x + 3y = 100. Clearly, (0, 0) does not satisfies the inequation 4x + 3y ≥ 100. So, the region in xy-plane that does not contains the origin represents the solution set of the given equation.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations.
These lines are drawn using a suitable scale.
The feasible region determined by the system of constraints is
The corner points are D0, 1003, E24, 43 and A 803, 0.
The values of Z at these corner points are as follows:
| Corner point | Z= 4x + 6y |
| D 0, 1003 | 200 |
| E 24, 43 | 104 |
| A 803, 0 | 3203 |
The minimum value of Z is Rs 104 which is at E24, 43 .
Q7.
Answer :
Let young man drives x km at a speed of 25 km/hr and y km at a speed of 40 km/hr.
Clearly, x,y≥0
It is given that, he spends Rs 2 per km if he drives at a speed of 25 km/hr and Rs 5 per km if he drives at a speed of 40 km/hr. Therefore, money spent by him when he travelled x km and y km is Rs 2x and Rs 5y respectively.
It is given that he has a maximum of Rs 100 to spend.
Thus, 2x+5y≤100
Time spent by him when travelling with a speed of 25 km/hr =x25hrTime spent by him when travelling with a speed of 40 km/hr =x40hr
Also, the available time is of 1 hour.
x25+y40≤1⇒40x+25y≤1000
The distance covered is Z = x+y which is to be maximised.
Thus, the mathematical formulation of the given linear programmimg problem is
Max Z = x+y
subject to
2x+5y≤10040x+25y≤1000
x,y≥0
First we will convert inequations into equations as follows:
2x + 5y = 100, 40x + 25y = 1000, x = 0 and y = 0
Region represented by 2x + 5y ≤ 100:
The line 2x + 5y = 100 meets the coordinate axes at A50, 0 and B0, 20 respectively. By joining these points we obtain the line
2x + 5y = 100. Clearly (0,0) satisfies the 2x + 5y = 100. So,the region which contains the origin represents the solution set of the inequation 2x + 5y ≤ 100.
Region represented by 40x + 25y ≤ 1000:
The line 40x + 25y = 1000 meets the coordinate axes at C25, 0 and D0, 40 respectively. By joining these points we obtain the line
2x + y = 12.Clearly (0,0) satisfies the inequation 40x + 25y ≤ 1000. So,the region which contains the origin represents the solution set of the inequation 40x + 25y ≤ 1000.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints 2x + 5y ≤ 100, 40x + 25y ≤ 1000, x ≥ 0, and y ≥ 0 are as follows
The corner points are O(0, 0), B(0, 20), E503, 403 and C(25, 0).
The values of Z at these corner points are as follows
| Corner point | Z = x + y |
| O | 0 |
| B | 20 |
| E | 30 |
| C | 25 |
The maximum value of Z is 30 which is attained at E.
Thus, the maximum distance travelled by the young man is 30 kms, if he drives 503 km at a speed of 25 km/hr and 403km at a speed of 40 km/hr .
Q8.
Answer :
Let the cereal contain x kg of bran and y kg of rice.
Therefore, x,y≥0
The given information can be tabulated as follows
| Protein(grams) | Iron(milligrams) | |
| Bran | 80 | 40 |
| Rice | 100 | 30 |
| minimum requirement | 88 | 36 |
Bran and rice contains at least 88 grams of protein and at least 36 milligrams of iron.
Thus,the constraints are
80x+100y≥8840x+30y≥36
It is given that bran costs Rs 5 per kg and rice costs Rs 4 per kg. Therefore, cost of x kg of bran and y kg of rice is Rs 5x and Rs 4y respectively.
Hence, total profit is Rs (5x + 4y)
Let Z denote the total cost.
∴ Z = 5x+4y
Thus, the mathematical formulation of the given problem is
Minimize Z=5x+4y
subject to
80x+100y≥8840x+30y≥36
x,y≥0
First we will convert inequations into equations as follows :
80x + 100y = 60, 40x + 30y = 36, x = 0 and y = 0
Region represented by 80x + 100y ≥ 88:
The line 80x + 100y = 60 meets the coordinate axes at A(1.1, 0) and B(0, 0.88)respectively. By joining these points we obtain the line 80x + 100y = 60. Clearly (0,0) does not satisfies the 80x + 100y ≥ 88. So,the region which does not contains the origin represents the solution set of the inequation
80x + 100y ≥ 88.
Region represented by 40x + 30y ≥ 36:
The line 40x + 30y = 36 meets the coordinate axes at C(0.9, 0) and D(0, 1.2) respectively. By joining these points we obtain the line 40x + 30y = 36.
Clearly (0,0) does not satisfies the inequation 40x + 30y ≥ 36. So,the region which does not contains the origin represents the solution set of the inequation 40x + 30y ≥ 36.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints 80x + 100y ≥ 88, 40x + 30y ≥ 36, x ≥ 0, and y ≥ 0 are as follows.
The feasible region determined by the system of constraints is
The corner points are D(0, 1.2), E(0.6, 0.4) and A(1.1, 0).
The values of Z at these corner points are as follows:
| Corner point | Z = 5x + 4y |
| D(0, 1.2) | 4.8 |
| E(0.6, 0.4) | 4.6 |
| A(1.1, 0) | 5.5 |
The minimum value of Z is 4.6 which is attained at E(0.6, 0.4).
Hence, the minimum cost is Rs 4.6.
Page 30.51 Ex.30.3
Q9.
Answer :
Let x units of item A and y units of item B be manufactured.
Therefore, x,y≥0
As we are given,
| Item | Number of hours required by the machine | ||
| A B | I | II | III |
| 1 2 | 2 1 | 1 5/4 | |
Machines I and II are capable of being operated for at most 12 hours whereas Machine III must operate at least for 5 hours a day.
According to question, the constraints are
x+2y≤122x+y≤12x+54y≥5
He makes a profit of Rs 6.00 on item A and Rs 4.00 on item B.
Profit made by him in producing x items of A and y items of B is 6x + 4y.
Total profit Z = 6x+4y which is to be maximised
Thus, the mathematical formulation of the given linear programmimg problem is
Max Z = 6x+4y
subject to
x+2y≤122x+y≤12x+54y≥5
x,y≥0
First we will convert inequations into equations as follows :
x + 2y = 12, 2x + y = 12, x+54y=5, x = 0 and y = 0
Region represented by x + 2y ≤ 12:
The line x + 2y = 12 meets the coordinate axes at A1(12, 0) and B1(0, 6) respectively. By joining these points we obtain the line x + 2y = 12.Clearly (0,0) satisfies the x + 2y = 12. So, the region which contains the origin represents the solution set of the inequation x + 2y ≤ 12.
Region represented by 2x + y ≤ 12:
The line 2x + y = 12 meets the coordinate axes at C1(6, 0) and D1(0, 12) respectively. By joining these points we obtain the line 2x + y = 12. Clearly (0,0) satisfies the inequation 2x + y ≤ 12. So,the region which contains the origin represents the solution set of the inequation 2x + y ≤ 12.
Region represented by x+54y≥5:
The line x+54y=5 meets the coordinate axes at E1(5, 0) and F1(0, 4) respectively. By joining these points we obtain the line
x+54y=5. Clearly (0,0) does not satisfies the inequation x+54y≥5. So,the region which does not contains the origin represents the solution set of the inequation x+54y≥5.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints x + 2y ≤ 12, 2x + y ≤ 12, x+54y≥5, x ≥ 0, and y ≥ 0 are as follows.
The corner points are B1(0, 6), G1(4, 4), C1(6, 0), E1(5, 0) and F1(0, 4).
The values of Z at these corner points are as follows
| Corner point | Z = 6x + 4y |
| B1 | 24 |
| G1 | 40 |
| C1 | 36 |
| E1 | 30 |
| F1 | 16 |
The maximum value of Z is 40 which is attained at G1(4, 4).
Thus, the maximum profit is Rs 40 obtained when 4 units each of item A and B are manufactured.
Q11.
Answer :
Let the factory manufacture x screws of type A and y screws of type B on each day. Therefore,
x ≥ 0 and y ≥ 0
The given information can be compiled in a table as follows.
| Screw A | Screw B | Availability | |
| Automatic Machine (min) | 4 | 6 | 4 × 60 = 240 |
| Hand Operated Machine (min) | 6 | 3 | 4 × 60 = 240 |
The manufacturer can sell a package of screws ‘A’ at a profit of Rs 0.7 and screws ‘B’ at a profit of Re 1.
Total profit, Z = 0.7x + 1y
The mathematical formulation of the given problem is
Maximize Z = 0.7x + 1y
subject to the constraints,
x, y ≥ 0
First we will convert inequations into equations as follows:
4x + 6y = 240, 6x + 3y = 240, x = 0 and y = 0
Region represented by 4x + 6y ≤ 240:
The line 4x + 6y = 240 meets the coordinate axes at A1(60, 0) and B1(0, 40) respectively. By joining these points we obtain the line 4x + 6y = 240.Clearly (0,0) satisfies the 4x + 6y = 240. So,the region which contains the origin represents the solution set of the inequation 4x + 6y ≤ 240.
Region represented by 6x + 3y ≤ 240:
The line 6x + 3y = 240 meets the coordinate axes at C1(40, 0) and D1(0, 80) respectively. By joining these points we obtain the line 6x + 3y = 240. Clearly (0,0) satisfies the inequation 6x + 3y ≤ 240. So,the region which contains the origin represents the solution set of the inequation 6x + 3y ≤ 240.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints 4x + 6y ≤ 240, 6x + 3y ≤ 240, x ≥ 0, and y ≥ 0 are as follows.
The corner points are C1(40, 0), E1(30, 20) and B1(0, 40).
The values of Z at these corner points are as follows.
| Corner point | Z = 7x + 10y |
| C1(40, 0) | 280 |
| E1(30, 20) | 410 |
| B1(0, 40) | 400 |
The maximum value of Z is 410 at (30, 20).
Thus, the factory should produce 30 packages of screws A and 20 packages of screws B to get the maximum profit of Rs 410.
Q12.
Answer :
Let the company produces x belts of type A and y belts of type B.
Number of belts cannot be negative.
Therefore, x,y≥0
It is given that leather is sufficient only for 800 belts per day (both A and B combined). Therefore,
x + y ≤ 800
It is given that the rate of production of belts of type B is 1000 per day.Hence, the time taken to produce y belts of type B is y1000.
And, since each belt of type A requires twice as much time as a belt of type B, the rate of production of belts of type A is 500 per day and therefore, total time taken to produce x belts of type A is x500.Thus, we have
x500+y1000≤1⇒2x+y≤1000
Belt A requires a fancy buckle and only 400 fancy buckles are available for this per day.
x ≤ 400
For belt of type B, only 700 buckles are available per day.
y ≤ 700
Profits on each type of belt are Rs 2 and Rs 1.50 per belt, respectively. Therefore, profit gained on x belts of type A and y belts of type B is Rs 2x and
Rs 1.50y respectively.Hence, the total profit would be Rs (2x + 1.50y).
Let Z denote the total profit.
∴ Z = 2x+1.5y
Thus, the mathematical formulation of the given linear programming problem is
Max Z = 2x+1.5y
subject to
x+y≤8002x+y≤1000x≤400y≤700
x,y≥0
First we will convert inequations into equations as follows :
x + y = 800, 2x + y = 1000, x = 400, y = 700, x = 0 and y = 0
Region represented by x + y ≤ 800:
The line x + y = 800 meets the coordinate axes at A1(800, 0) and B1(0, 800) respectively. By joining these points we obtain the line x + y = 800. Clearly (0,0) satisfies the x + y = 800. So, the region which contains the origin represents the solution set of the inequation x + y ≤ 800.
Region represented by 2x + y ≤ 1000:
The line 2x + y = 1000 meets the coordinate axes at C1(500, 0) and D1(0, 1000) respectively. By joining these points we obtain the line 2x + y = 1000. Clearly (0,0) satisfies the inequation 2x + y ≤ 1000. So,the region which contains the origin represents the solution set of the inequation 2x + y ≤ 1000.
Region represented by x ≤ 400:
The line x = 400 will pass through E1(400, 0). The region to the left of the line x = 400 will satisfy the inequation x ≤ 400.
Region represented by y ≤ 700:
The line y = 700 will pass through F1(0, 700). The region below the line y = 700 will satisfy the inequation y ≤ 700.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints x + y ≤ 800, 2x + y ≤ 1000, x ≤ 400, y ≤ 700, x ≥ 0, and y ≥ 0 are as follows.
The feasible region determined by the system of constraints is
The corner points are F1(0, 700), G1(200, 600), H1(400, 200) and E1(400, 0).
The values of Z at these corner points are as follows
| Corner point | Z= 2x +1.5y |
| F1(0, 700) | 1050 |
| G1(200, 600) | 1300 |
| H1(400, 200) | 1100 |
| E1(400, 0) | 800 |
The maximum value of Z is 1300 which is attained at G1(200, 600).
Thus, the maximum profit is Rs 1300 obtained when 200 belts of type A and 600 belts of type B were produced.
Q13.
Answer :
Let x articles of deluxe model and y articles of an ordinary model be made.
Number of articles cannot be negative.
Therefore, x,y≥0
According to the question, the making of a deluxe model requires 2 hrs. work by a skilled man and the ordinary model requires 1 hr by a skilled man
2x+y≤40
The making of a deluxe model requires 2 hrs. work by a semi-skilled man ordinary model requires 3 hrs. work by a semi-skilled man.
2x+3y≤80
Total profit = Z = 15x+10y which is to be maximised
Thus, the mathematical formulation of the given linear programmimg problem is
Max Z = 15x+10y
subject to
2x+y≤402x+3y≤80
x≥0y≥0
The feasible region determined by the system of constraints is
The corner points are A(0,803), B(10, 20), C(20, 0)
The values of Z at these corner points are as follows:
| Corner point | Z= 15x+10y |
| A | 8003 |
| B | 350 |
| C | 300 |
The maximum value of Z is 300 which is attained at C(20, 0)
Thus, the maximum profit is Rs 300 obtained when 10 units of deluxe model and 20 unit of ordinary model is produced
Page 30.52 Ex.30.3
Q14.
Answer :
Let x units of type A and y units of type B cups were made.
Quantities cannot be negative.Therefore,
x,y≥0
As we are given,
| Machines | |||
| I | II | III | |
| A B | 12 6 | 18 0 | 6 9 |
Every machine is available for a maximum of 6 hours per day i.e. 360 minutes per day.
Therefore, the constraints are
12x+6y≤36018x+0y≤3606x+9y≤360
If the profit on each cup A is 75 paise and that on each cup B is 50 paise.
Total profit = Z = 0.75x+0.50y which is to be maximised.
Thus, the mathematical formulation of the given linear programmimg problem is
Max Z = 0.75x+0.50y
subject to
12x+6y≤36018x+0y≤3606x+9y≤360
x,y≥0
First we will convert inequations into equations as follows :
12x + 6y = 360, 18x = 360, 6x+9y=360, x = 0 and y = 0
Region represented by 12x + 6y ≤ 360:
The line 12x + 6y = 360 meets the coordinate axes at A1(30, 0) and B1(0, 60) respectively. By joining these points we obtain the line 12x + 6y = 360.Clearly (0,0) satisfies the 12x + 6y = 360. So,the region which contains the origin represents the solution set of the inequation 12x + 6y ≤ 360.
Region represented by 18x + 0y ≤ 360:
The line 18x + 0y = 360 meets the coordinate axes at C1(20, 0) . We obtain the line 18x + 0y = 360.Clearly (0,0) satisfies the inequation 18x + 0y ≤ 360. So,the region which contains the origin represents the solution set of the inequation 18x + 0y ≤ 360.
Region represented by 6x+9y≤360:
The line 6x+9y=360 meets the coordinate axes at E1(60, 0) and F1(0, 40) respectively. By joining these points we obtain the line 6x+9y=360. Clearly (0,0) satisfies the inequation 6x+9y≤360 . So,the region which contains the origin represents the solution set of the inequation 6x+9y≤360.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints 12x + 6y ≤ 360, 18x + 0y ≤ 360, 6x+9y≤360, x ≥ 0, and y ≥ 0 are as follows..
The corner points are O(0, 0) F1(0, 40), G1(15, 30), H1(20, 20) and C1(20, 0).
The values of Z at these corner points are as follows
| Corner point | Z= 0.75x + 0.50y |
| O | 0 |
| F1 | 20 |
| G1 | 26.25 |
| H1 | 25 |
| C1 | 15 |
Thus, the maximum profit is Rs 26.25 obtained when 15 units of type A and 30 units of type B cups were made.
Q15.
Answer :
Let x machines of type A and y machines of type B were purchased.
Number of machines cannot be negative.
Therefore, x,y≥0
We are given,
| Area occupied by the machine | Labour force for each machine | Daily output in units | |
| Machine A Machine B | 1000 sq. m 1200 sq. m | 12 men 8 men | 60 40 |
The area of 7600 sq m is available and there are 72 skilled men available to operate the machines.
Therefore, the constraints are
1000x+1200y≤7600and 12x+8y≤72
Total daily output = Z = 60x+40y which is to be maximised.
Thus, the mathematical formulation of the given linear programming problem is
Max Z = 60x+40y
subject to
1000x+1200y≤760012x+8y≤72
x,y≥0
First we will convert inequations into equations as follows :
1000x + 1200y = 7600, 12x + 8y = 72, x = 0 and y = 0
Region represented by 1000x + 1200y ≤ 7600:
The line 1000x + 1200y = 7600 meets the coordinate axes at A1385, 0 and B10, 193 respectively. By joining these points we obtain the line
1000x + 1200y = 7600. Clearly (0,0) satisfies the 1000x + 1200y = 7600. So, the region which contains the origin represents the solution set of the inequation 1000x + 1200y ≤ 7600.
Region represented by 12x + 8y ≤ 72:
The line 12x + 8y = 72 meets the coordinate axes at C1(6, 0) and D1(0, 9) respectively. By joining these points we obtain the line 12x + 8y = 72 .Clearly (0,0) satisfies the inequation 12x + 8y ≤ 72. So,the region which contains the origin represents the solution set of the inequation 12x + 8y ≤ 72.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints 1000x + 1200y ≤ 7600, 12x + 8y ≤ 72, x ≥ 0, and y ≥ 0 are as follows.
The corner points are O(0, 0) B10, 193, E1(4, 3), C1(6, 0)
The values of Z at these corner points are as follows
| Corner point | Z= 60x + 40y |
| O | 0 |
| B1 | 253.3 |
| E1 | 360 |
| C1 | 360 |
The maximum value of Z is 360 which is attained at E1(4, 3) and C1(6, 0).
Thus, the maximum output is Rs 360 obtained when 4 units of type A and 3 units of type B or 6 units of type A are manufactured.
Q16.
Answer :
Let x goods of type A and y goods of type B were produced.
Number of goods cannot be negative.
Therefore, x,y≥0
The given information can be tabulated as follows:
| Silver(gm) | Gold white(gm) | |
| Type A | 3 | 1 |
| Type B | 1 | 2 |
| Availability | 9 | 8 |
Therefore, the constraints are
3x+y≤9x+2y≤8
If each unit of type A brings a profit of Rs 40 and that of type B Rs 50.Then, x goods of type A and y goods of type B brings a profit of Rs 40x and Rs 50y.
Total profit = Z = 40x+50y which is to be maximised.
Thus, the mathematical formulation of the given linear programmimg problem is
Max Z = 40x+50y
subject to
3x+y≤9x+2y≤8
x,y≥0
First we will convert inequations into equations as follows :
3x + y = 9, x + 2y = 8, x = 0 and y = 0
Region represented by 3x + y ≤ 9:
The line 3x + y = 9 meets the coordinate axes at A1(3, 0) and B1(0, 9) respectively. By joining these points we obtain the line
3x + y = 9.Clearly (0,0) satisfies the 3x + y = 9. So,the region which contains the origin represents the solution set of the inequation
3x + y ≤ 9.
Region represented by x + 2y ≤ 8:
The line x + 2y = 8 meets the coordinate axes at C1(8, 0) and D1(0, 4) respectively. By joining these points we obtain the line
x + 2y = 8.Clearly (0,0) satisfies the inequation x + 2y ≤ 8. So,the region which contains the origin represents the solution set of the inequation x + 2y ≤ 8.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints 3x + y ≤ 9, x + 2y ≤ 8, x ≥ 0, and y ≥ 0 are as follows.
The corner points are O(0, 0), D1(0, 4), E1(2, 3), A1(3, 0)
The values of Z at these corner points are as follows
| Corner point | Z = 40x + 50y |
| O | 0 |
| D1 | 200 |
| E1 | 230 |
| A1 | 120 |
The maximum value of Z is 230 which is attained at E1(2, 3).
Thus, the maximum profit is of Rs 230 obtained when 2 units of type A and 3 units of type B produced.
Q17.
Answer :
Let x chairs and y tables were produced.
Number of chairs and tables cannot be negative.
Therefore, x,y≥0
The given information can be tabulated as follows:
| Time on machine A(hrs) | Time on machine B (hrs) | |
| Chairs | 2 | 6 |
| Tables | 4 | 2 |
| Availability | 16 | 30 |
Therefore, the constraints are
2x+4y≤166x+2y≤30
Profit gained by the manufacturer from a chair and a table is Rs 3 and Rs 5 respectively.Therefore, profit gained from x chairs and y tables is Rs 3x and Rs 5y.
Total profit = Z = 3x+5y which is to be maximised
Thus, the mathematical formulation of the given linear programmimg problem is
Max Z = 3x+5y
subject to
2x+4y≤166x+2y≤30
x,y≥0
First we will convert inequations into equations as follows:
2x + 4y = 16, 6x + 2y =30, x = 0 and y = 0
Region represented by 2x + 4y ≤ 16:
The line 2x + 4y = 16 meets the coordinate axes at A1(8, 0) and B1(0, 4) respectively. By joining these points we obtain the line 2x + 4y = 16. Clearly (0,0) satisfies the 2x + 4y = 16. So, the region which contains the origin represents the solution set of the inequation 2x + 4y ≤ 16.
Region represented by 6x + 2y ≤ 30:
The line 6x + 2y =30 meets the coordinate axes at C1(5, 0) and D1(0, 15) respectively. By joining these points we obtain the line 6x + 2y =30 .Clearly (0,0) satisfies the inequation 6x + 2y ≤ 30. So,the region which contains the origin represents the solution set of the inequation 6x + 2y ≤ 30.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints 2x + 4y ≤ 16, 6x + 2y ≤ 30, x ≥ 0, and y ≥ 0 are as follows.
The corner points are O(0, 0), B1(0, 4), E1225,95 and C1(5, 0).
The values of Z at these corner points are as follows
| Corner point | Z= 3x + 5y |
| O | 0 |
| B1 | 20 |
| E1 | 22.2 |
| C1 | 15 |
The maximum value of Z is 22.2 which is attained at B1225,95.
Thus, the maximum profit is of Rs 22.20 obtained when 225 units of chairs and 95 units of tables are produced.
Q18.
Answer :
Let x units of chairs and y units of tables were produced
Therefore, x,y≥0
The given information can be tabulated as follows:
| Wood(square feet) | Man hours | |
| Chairs(x) | 5 | 10 |
| Tables(y) | 20 | 25 |
| Availability | 400 | 450 |
Therefore, the constraints are
5x+20y≤40010x+25y≤450
It is known that to make a chair requires 5 square feet of wood and 10 man-hours and yields a profit of Rs 45, while each table uses 20 square feet of wood and 25 man-hours and yields a profit of Rs 80.
Therefore, profit gained to make x chairs and y tables is Rs 45x and Rs 80y respectively.
Total profit = Z = 45x+80y which is to be maximised.
Thus, the mathematical formulation of the given linear programmimg problem is
Max Z = 45x+80y
subject to
5x+20y≤40010x+25y≤450
x,y≥0
First we will convert inequations into equations as follows:
5x + 20y = 400, 10x + 25y = 450, x = 0 and y = 0
Region represented by 5x + 20y ≤ 400:
The line 5x + 20y = 400 meets the coordinate axes at A80, 0 and B0, 20 respectively. By joining these points we obtain the line
5x + 20y = 400 . Clearly (0,0) satisfies the 5x + 20y = 400 . So, the region which contains the origin represents the solution set of the inequation 5x + 20y ≤ 400.
Region represented by 10x + 25y ≤ 450:
The line 10x + 25y = 450 meets the coordinate axes at C45, 0 and D0, 18 respectively. By joining these points we obtain the line
10x + 25y = 450. Clearly (0,0) satisfies the inequation 10x + 25y ≤ 450. So,the region which contains the origin represents the solution set of the inequation 10x + 25y ≤ 450.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints 5x + 20y ≤ 400, 10x + 25y ≤ 450, x ≥ 0, and y ≥ 0 are as follows.
The corner points are A(0, 18), B(45, 0)
The values of Z at these corner points are as follows
| Corner point | Z= 45x + 80y |
| A | 1440 |
| B | 2025 |
The maximum value of Z is 2025 which is attained at B45, 0.
Thus, the maximum profit is of Rs 2025 obtained when 45 units of chairs and no units of tables are produced
Q19.
Answer :
Let x kg of kind A and y kg of kind B were used.
Quantity cannot be negative.
Therefore, x,y≥0
The given information can be tabulated as follows:
| Nut | Almonds(grams) | Cashewnuts(grams) | Hazel nuts(grams) |
| A(x) | 60 | 30 | 30 |
| B(y) | 30 | 60 | 180 |
| Availability | 240 | 300 | 540 |
Therefore, the constraints are
60x+30y≥24030x+60y≥30030x+180y≥540
Mixture A costs Rs 8 per kg. and mixture B costs Rs 12 per kg.
Total cost = Z = 8x+12y which is to be minimised.
Thus, the mathematical formulation of the given linear programmimg problem is
Min Z = 8x+12y
subject to
2x+y≥8 x+2y≥10 x+6y≥18
x,y≥0
First, we will convert the given inequations into equations, we obtain the following equations:
2x + y = 8, x +2y = 10, x +6y = 18, x = 0 and y = 0
Region represented by 2x + y ≥ 8:
The line 2x + y = 8 meets the coordinate axes at A1(4, 0) and B1(0, 8) respectively. By joining these points we obtain the line 2x + y = 8.
Clearly (0,0) does not satisfies the inequation 2x + y ≥ 8. So,the region in xy plane which does not contain the origin represents the solution set of the inequation 2x + y ≥ 8.
Region represented by x +2y ≥ 10:
The line x +2y = 10 meets the coordinate axes at C1(10,0) and D1(0, 5) respectively. By joining these points we obtain the line
x +2y = 10. Clearly (0,0) does not satisfies the inequation x +2y ≥ 10. So,the region which does not contain the origin represents the solution set of the inequation x +2y ≥ 10.
Region represented by x +6y ≥ 18:
The line x +6y = 18 meets the coordinate axes at E1(18,0) and F1(0, 3) respectively. By joining these points we obtain the line x + 6y = 18.Clearly (0,0) does not satisfies the inequation x + 6y ≥ 18. So,the region which does not contain the origin represents the solution set of the inequation x +6y ≥ 18.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints 2x + y ≥ 8, x + 2y ≥ 10,x + 6y ≥ 18, x ≥ 0, and y ≥ 0, are as follows.
The corner points are B1(0, 8), G1(2, 4), H1(6, 2) and E1(18, 0).
The values of Z at these corner points are as follows
| Corner point | Z= 8x + 12y |
| B1 | 96 |
| G1 | 64 |
| H1 | 72 |
| E1 | 144 |
The minimum value of Z is 64 which is attained at G12, 4.
Thus, the minimum cost is Rs 64 obtained when 2 units of kind A and 4 units of kind B nuts were used.
Page 30.53 Ex.30.3
Q20.
Answer :
Let x products of type A and y products of type B are manufactured.
Number of products cannot be negative.
Therefore, x,y≥0
The given information can be tabulated as follows:
| Product | M1(minutes) | M2(minutes) |
| A(x) | 4 | 8 |
| B(y) | 4 | 4 |
| Availability | 500 | 600 |
Therefore, the constraints are
4x+4y≤5008x+4y≤600
The products A and B are sold at a profit of Rs 3 and Rs 4 respectively. Therefore, Profit gained from x products of type A and y products of type B is Rs 3x and Rs 4y respectively.
Total profit = Z = 3x + 4y which is to be maximised.
Thus, the mathematical formulation of the given linear programmimg problem is
Max Z = 3x+4y
subject to
4x+4y≤5008x+4y≤600
First we will convert inequations into equations as follows:
4x + 4y = 500, 8x + 4y = 600, x = 0 and y = 0
Region represented by 4x + 4y ≤ 500:
The line 4x + 4y = 500 meets the coordinate axes at A1(125, 0) and B1(0, 125) respectively. By joining these points we obtain the line
4x + 4y = 500. Clearly (0,0) satisfies the 5x + 20y = 400 . So, the region which contains the origin represents the solution set of the inequation 5x + 20y ≤ 400.
Region represented by 8x + 4y ≤ 600:
The line 8x + 4y = 600 meets the coordinate axes at C1(75, 0) and D1(0, 150) respectively. By joining these points we obtain the line
8x + 4y = 600. Clearly (0,0) satisfies the inequation 8x + 4y ≤ 600. So,the region which contains the origin represents the solution set of the inequation
8x + 4y ≤ 600.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints 4x + 4y ≤ 500, 8x + 4y ≤ 600, x ≥ 0, and y ≥ 0 are as follows:
The corner points are O(0, 0), B1(0, 125), E1(25, 100) and C1(75, 0).
The values of Z at these corner points are as follows:
| Corner point | Z= 3x + 4y |
| O | 0 |
| B1 | 500 |
| E1 | 475 |
| C1 | 225 |
The maximum value of Z is 500 which is attained at B1(0, 125).
Thus, the maximum profit is Rs 500 obtained when no units of product A and 125 units of product B were manufactured.
Q21.
Answer :
Let x units of item A and y units of item B were manufactured.
Number of items cannot be negative.
Therefore, x,y≥0
The given information can be tabulated as follows:
| Product | Motors | Transformers |
| A(x) | 3 | 4 |
| B(y) | 2 | 4 |
| Availability | 210 | 300 |
Further, it is given that type B is an export model, whose supply is restricted to 65 units per month.
Therefore, the constraints are
3x+2y≤2104x+4y≤300y≤65
A and B can make a profit of Rs 20 per unit of A and Rs 30 per unit of B.Therefore, profit gained from x units of item A and y units of item B is Rs 20x and Rs 30y respectively.
Total profit = Z = 20x+30y which is to be maximised.
Thus, the mathematical formulation of the given linear programmimg problem is
Max Z = 20x+30y
subject to
3x+2y≤2104x+4y≤300y≤65
x,y≥0
First we will convert inequations into equations as follows:
3x + 2y = 210, 4x + 4y = 300, y = 65, x = 0 and y = 0
Region represented by 3x + 2y ≤ 210:
The line 3x + 2y = 210 meets the coordinate axes at A1(70, 0) and B1(0, 105) respectively. By joining these points we obtain the line 3x + 2y = 210.Clearly (0,0) satisfies the 3x + 2y = 210. So,the region which contains the origin represents the solution set of the inequation 3x + 2y ≤ 210.
Region represented by 4x + 4y ≤ 300:
The line 4x + 4y = 300 meets the coordinate axes at C1(75, 0) and D1(0, 75) respectively. By joining these points we obtain the line
4x + 4y = 300.Clearly (0,0) satisfies the inequation 4x + 4y ≤ 300. So,the region which contains the origin represents the solution set of the inequation
4x + 4y ≤ 300.
y = 65 is the line passing through the point E1(0, 65) and is parallel to X axis.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints 3x + 2y ≤ 210, 4x + 4y ≤ 300, y ≤ 65, x ≥ 0, and y ≥ 0 are as follows:
The corner points are O(0, 0), E1(0, 65), G110, 65, F1(60, 15) and A1(70, 0).
The values of Z at these corner points are as follows:
| Corner point | Z= 20x + 30y |
| O | 0 |
| E1 | 1950 |
| G1 | 2150 |
| F1 | 1650 |
| A1 | 1400 |
The maximum value of Z is 2150 which is attained at G110, 65.
Thus, the maximum profit is Rs 2150 obtained when 10 units of item A and 65 units of item B were manufactured.
Q22.
Answer :
Let x units of first product and y units of second product be manufactured.
Therefore, x,y≥0
The given information can be tabulated as follows:
| Product | Resource A | Resource B | Resource C |
| First(x) | 2 | 2 | 4 |
| Second(y) | 4 | 2 | 0 |
| Availability | 20 | 12 | 16 |
Therefore, the constraints are
2x+4y≤202x+2y≤124x+0y≤16 or 4x≤16
It is known that the first product gives a profit of 2 monetary units per unit and the second 3. Therefore, profit gained from x units of first product and y units of second product is 2x monetary units and 4y monetary units respectively.
Total profit = Z = 2x+3y which is to be maximised
Thus, the mathematical formulation of the given linear programmimg problem is
Max Z = 2x+3y
subject to
2x+4y≤202x+2y≤124x+0y≤16 or 4x≤16
x,y≥0
First we will convert inequations into equations as follows :
2x + 4y = 20, 2x + 2y = 12, 4x = 16, x = 0 and y = 0
Region represented by 2x + 4y ≤ 20:
The line 2x + 4y = 20 meets the coordinate axes at A1(10, 0) and B1(0, 5) respectively. By joining these points we obtain the line 2x + 4y = 20.Clearly (0,0) satisfies the 3x + 2y = 210. So,the region which contains the origin represents the solution set of the inequation 2x + 4y ≤ 20.
Region represented by 2x + 2y ≤ 12:
The line 2x +2y =16 meets the coordinate axes at C1(6, 0) and D1(0, 6) respectively. By joining these points we obtain the line 2x + 2y = 12.Clearly (0,0) satisfies the inequation 2x + 2y ≤ 12. So, the region which contains the origin represents the solution set of the inequation 2x + 2y ≤ 12.
Region represented by 4x ≤ 16:
The line 4x =16 or x = 4 is the line passing through the point E1(4, 0) and is parallel to Y axis.The region to the left of the line x = 4 would satisfy the inequation 4x ≤ 16.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints 2x + 4y ≤ 20, 2x + 2y ≤ 12, 4x ≤ 16, x ≥ 0 and y ≥ 0 are as follows
The corner points are O(0, 0), B1(0, 5), G12, 4, F1(4, 2) and E1(4, 0).
The values of Z at these corner points are as follows:
| Corner point | Z= 2x + 3y |
| O | 0 |
| B1 | 15 |
| G1 | 16 |
| F1 | 14 |
| E1 | 8 |
The maximum value of Z is 16 which is attained at G12, 4.
Thus, the maximum profit is 16 monetary units obtained when 2 units of first product and 4 units of second product were manufactured.
Q23.
Answer :
Let the sale of hand cover edition be ‘h’ and that of paperback editions be ‘t’.
SP of a hard cover edition of the textbook = Rs 72
SP of a paperback edition of the textbook = Rs 40
Cost to the publisher for hard cover edition = Rs 56
Cost to the publisher for a paperback edition = Rs 28
Weekly cost to the publisher = Rs 9600
Profit to be maximised, Z = (72 − 56) h + (40 − 28) t − 9600
⇒ Z = 16h + 12t − 9600
5 (h + t) ≤ 4800
10 h + 2t ≤ 4800
The corner points are O(0, 0), B1(0, 960), E1(360, 600) and F1(480, 0).
The values of Z at these corner points are as follows:
| Corner point | Z = 16h + 12t − 9600 |
| O | −9600 |
| B1 | 1920 |
| E1 | 3360 |
| F1 | −1920 |
The maximum value of Z is 3360 which is attained at E1(360, 600).
The maximum profit is 3360 which is obtained by selling 360 copies of hardcover edition and 600 copies of paperback edition.
Q24.
Answer :
Let the number of size A pill be x and the number of size B pill be y.
Therefore, the constraints are
2x+y≥12 5x+8y≥7.4x+66y≥24
Z = x+y which is to be minimised
The corner points are (0, 12), (24, 0) and 768131, 36131.
The values of Z at these corner points are as follows:
| Corner point | Z = x + y |
| (0, 12) | 12 |
| (24, 0) | 24 |
| 768131, 36131 | 6.1373 |
The minimum value of Z is 6.1373 but the region is unbounded so check whether x + y < 6.1373 has common region with the feasible solution.
Clearly, it can be seen that it doesn’t has any common region.
So,
x=768131, y=36131
This is the least quantity of pill A and B.
Codline quantity⇒768131+66×36131 ⇒24 grains
Disclaimer: The answer provided in the book is incorrect.
Q25.
Answer :
Let x kg of compound A and y kg of compound B were produced.
Quantity cannot be negative.
Therefore, x,y≥0
| Compound | Minimum requirement | ||
| A | B | ||
| Ingredient C Ingredient D | 1 3 | 2 1 | 80 75 |
| Cost (in Rs) per kg | 4 | 6 | |
According to question, the constraints are
x+2y≥803x+y≥75
Cost (in Rs) per kg of compound A and compound B is Rs 4 and Rs 6 respectively.Therefore, cost of x kg of compound A and y kg of compound B is 4x and 6y respectively.
Total cost = Z = 4x+6y which is to be minimised.
Thus, the mathematical formulation of the given linear programmimg problem is
Min Z = 4x+6y
subject to
x+2y≥803x+y≥75
x,y≥0
First we will convert inequations into equations as follows:
x + 2y = 80, 3x + y =75, x = 0 and y = 0
Region represented by x + 2y ≥ 80:
The line x + 2y = 80 meets the coordinate axes at A1(80, 0) and B1(0, 40) respectively. By joining these points we obtain the line x + 2y = 80. Clearly (0,0) does not satisfies the x + 2y = 80. So, the region which does not contain the origin represents the solution set of the inequation x + 2y ≥ 80.
Region represented by 3x + y ≥ 75:
The line 3x + y =75 meets the coordinate axes at C1(25, 0) and D1(0, 75) respectively. By joining these points we obtain the line 3x + y =75.Clearly (0,0) does not satisfies the inequation 3x + y ≥ 75. So,the region which does not contain the origin represents the solution set of the inequation 3x + y ≥ 75.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints x + 2y ≥ 80, 3x + y ≥ 75, x ≥ 0, and y ≥ 0 are as follows.
The corner points are D1(0, 75), E1(14, 33) and A1(80, 0).
The values of Z at these corner points are as follows:
| Corner point | Z= 4x + 6y |
| D1 | 450 |
| E1 | 254 |
| A1 | 320 |
The minimum value of Z is 254 which is attained at E114, 33.
Thus, the minimum cost is Rs 254 obtained when 14 units of compound A and 33 units of compound B were produced.
Q26.
Answer :
Let the company manufacture x souvenirs of type A and y souvenirs of type B.
Number of items cannot be negative.
Therefore,
x ≥ 0 and y ≥ 0
The given information can be complied in a table as follows.
| Type A | Type B | Availability | |
| Cutting(min) | 5 | 8 | 3 × 60 + 20 = 200 |
| Assembling(min) | 10 | 8 | 4 × 60 = 240 |
Therefore, the constraints are
The profit on type A souvenirs is 50 paise and on type B souvenirs is 60 paise.Therefore, profit gained on x souvenirs of type A and y souvenirs of type B is Rs 0.50x and Rs 0.60y respectively.
Total profit, Z = 0.5x + 0.6y
The mathematical formulation of the given problem is
Maximize Z = 0.5x + 0.6y
subject to the constraints,
x ≥ 0 and y ≥ 0
First we will convert inequations into equations as follows:
5x + 8y = 200, 10x + 8y = 240, x = 0 and y = 0
Region represented by 5x + 8y ≤ 200:
The line 5x + 8y = 200 meets the coordinate axes at A1(40, 0) and B1(0, 25) respectively. By joining these points we obtain the line
5x + 8y = 200 . Clearly (0,0) satisfies the 5x + 8y = 200. So, the region which contains the origin represents the solution set of the inequation 5x + 8y ≤ 200.
Region represented by 10x + 8y ≤ 240:
The line 10x + 8y = 240 meets the coordinate axes at C1(24, 0) and D1(0, 30) respectively. By joining these points we obtain the line
10x + 8y = 240. Clearly (0,0) satisfies the inequation 10x + 8y ≤ 240. So,the region which contains the origin represents the solution set of the inequation 10x + 8y ≤ 240.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints 5x + 8y ≤ 200, 10x + 8y ≤ 240, x ≥ 0 and y ≥ 0 are as follows.
The corner points of the feasible region are O(0, 0), B1(0, 25), E1(8, 20), C1(24, 0).
The values of Z at these corner points are as follows.
| Corner point | Z = 0.5x + 0.6y |
| O(0, 0) | 0 |
| B1(0, 25) | 15 |
| E1(8, 20) | 16 |
| C1(24, 0) | 12 |
The maximum value of Z is 160 at E1(8, 20).
Thus, 8 souvenirs of type A and 20 souvenirs of type B should be produced each day to get the maximum profit of Rs 16.
Page 30.54 Ex.30.3
Q27.
Answer :
Let x units of product A and y units of product B were manufactured.
Number of units cannot be negative.
Therefore, x,y≥0
According to question, the given information can be tabulated as:
| Selling price(Rs) | Manufacturing time(hrs) | |
| Product A(x) | 200 | 0.5 |
| Product B(y) | 300 | 1 |
Also, the availability of time is 40 hours and the revenue should be atleast Rs 10000.
Further, it is given that there is a permanent order for 14 units of product A and 16 units of product B.
Therefore, the constraints are
200x+300y≥100000.5x+y≤40x≥14y≥16
If the profit on each of product A is Rs 20 and on product B is Rs 30.Therefore, profit gained on x units of product A and y units of product B is Rs 20x and Rs 30y respectively.
Total profit = Z = 20x+30y which is to be maximised
Thus, the mathematical formulation of the given linear programmimg problem is
Max Z = 20x+30y
subject to
2x+3y≥100x+2y≤80x≥14y≥16
x,y≥0
First we will convert inequations into equations as follows:
2x + 3y = 100, x + 2y = 80, x = 14, y = 16, x = 0 and y = 0.
Region represented by 2x + 3y ≥ 100:
The line 2x + 3y = 100 meets the coordinate axes at A1(50, 0) and B10, 1003 respectively. By joining these points we obtain the line
2x + 3y = 100 . Clearly (0,0) does not satisfies the 2x + 3y = 100. So, the region which does not contain the origin represents the solution set of the inequation 2x + 3y ≥ 100.
Region represented by x + 2y ≤ 80:
The line x + 2y = 80 meets the coordinate axes at C1(80, 0) and D1(0, 40) respectively. By joining these points we obtain the line
x + 2y = 80. Clearly (0,0) satisfies the inequation x + 2y ≤ 80. So,the region which contains the origin represents the solution set of the inequation x + 2y ≤ 80.
Region represented by x ≥ 14
x = 14 is the line passes through (14, 0) and is parallel to the Y axis.The region to the right of the line x = 14 will satisfy the inequation.
Region represented by y ≥ 16
y = 16 is the line passes through (0, 16) and is parallel to the X axis.The region above the line y = 16 will satisfy the inequation.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints 2x + 3y ≥ 100, x + 2y ≤ 80, x ≥ 14, y ≥ 16, x ≥ 0 and y ≥ 0 are as follows.
The corner points of the feasible region are E1(26, 16), F1(48, 16), G1(14, 33) and H1(14, 24)
The values of Z at these corner points are as follows:
| Corner point | Z= 20x + 30y |
| E1 | 1000 |
| F1 | 1440 |
| G1 | 1270 |
| H1 | 1000 |
The maximum value of Z is Rs 1440 which is attained at F148, 16.
Thus, the maximum profit is Rs 1440 obtained when 48 units of product A and 16 units of product B were manufactured.
Q28.
Answer :
Let x trunks of first type and y trunks of second type were manufactured.
Number of trunks cannot be negative.Therefore,
x,y≥0
According to question, the given information can be tabulated as
| Machine A(hrs) | Machine B(hrs) | |
| First type(x) | 3 | 3 |
| Second type(y) | 3 | 2 |
| Availability | 18 | 15 |
Therefore, the constraints are
3x+3y≤183x+2y≤15
He earns a profit of Rs 30 and Rs 25 per trunk of the first type and the second type respectively.Therefore, profit gained by him from x trunks of first type and y trunks of second type is Rs 30x and Rs 25y respectively.
Total profit = Z = 30x+25y which is to be maximised
Thus, the mathematical formulation of the given linear programmimg problem is
Max Z = 30x+25y
subject to
3x+3y≤183x+2y≤15
x,y≥0
First we will convert inequations into equations as follows:
3x + 3y = 18, 3x + 2y = 15, x = 0 and y = 0
Region represented by 3x + 3y ≤ 18:
The line 3x + 3y = 18 meets the coordinate axes at A1(6, 0) and B1(0, 6) respectively. By joining these points we obtain the line 3x + 3y = 18. Clearly (0,0) satisfies the 3x + 3y = 18. So, the region which contains the origin represents the solution set of the inequation 3x + 3y ≤ 18.
Region represented by 3x + 2y ≤ 15:
The line 3x + 2y = 15 meets the coordinate axes at C1(5, 0) and D10, 152 respectively. By joining these points we obtain the line 3x + 2y = 15. Clearly (0,0) satisfies the inequation 3x + 2y ≤ 15. So,the region which contains the origin represents the solution set of the inequation 3x + 2y ≤ 15.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints 3x + 3y ≤ 18, 3x + 2y ≤ 15, x ≥ 0 and y ≥ 0 are as follows.
The corner points are O(0, 0), B1(0, 6), E1(3, 3) and C1(5, 0).
The values of Z at these corner points are as follows:
| Corner point | Z = 30x + 25y |
| O | 0 |
| B1 | 150 |
| E1 | 165 |
| C1 | 150 |
The maximum value of Z is 165 which is attained at E1(3, 3).
Thus, the maximum profit is Rs 165 obtained when 3 units of each type of trunk is manufactured.
Q29.
Answer :
Let x bottles of medicine A and y bottles of medicine B are prepared.
Number of bottles cannot be negative.
Therefore, x,y≥0
According to question, the constraints are
x≤20000y≤40000x+y≤45000
It takes 3 hours to prepare enough material to fill 1000 bottles of A, it takes 1 hour to prepare enough material to fill 1000 bottles of B
Time taken to fill one bottle of A is 31000hrs and time taken by to fill one bottle of B is 11000hrs.
Therefore, time taken to fill x bottles of A and y bottles of B is 3x1000hrs and y1000hrs respectively.
It is given that there are 66 hours available for this operation.
∴ 3×1000+y1000≤66
The profit is Rs 8 per bottle for A and Rs 7 per bottle for B.Therefore, profit gained on x bottles of medicine A and y bottles of medicine B is 8x and 7y respectively.
Total profit = Z = 8x+7y which is to be maximised.
Thus, the mathematical formulation of the given linear programmimg problem is
Max Z = 8x+7y
subject to
x≤20000y≤40000x+y≤45000
3×1000+y1000≤66⇒ 3x+y≤66000
x,y≥0
First we will convert inequations into equations as follows:
x =20000, y = 40000, x + y = 45000, 3x + y = 66000, x = 0 and y = 0
Region represented by x ≤ 20000:
The line x = 20000 is the line that passes through A1(20000, 0) and is parallel to Y axis.The region to the left of the line x = 20000 will satisfy the inequation x ≤ 20000.
Region represented by y ≤ 40000:
The line y = 40000 is the line that passes through B1(0, 40000) and is parallel to X axis.The region below the line y = 40000 will satisfy the inequation y ≤ 40000.
Region represented by x + y ≤ 45000:
The line x + y = 45000 meets the coordinate axes at C1(45000, 0) and D1(0, 45000) respectively. By joining these points we obtain the line x + y = 45000. Clearly (0,0) satisfies the inequation x + y ≤ 45000. So,the region which contains the origin represents the solution set of the inequation x + y ≤ 45000.
Region represented by 3x + y ≤ 66000:
The line 3x + y = 66000 meets the coordinate axes at E1(22000, 0) and F10, 66000 respectively. By joining these points we obtain the line 3x + y = 66000. Clearly (0,0) satisfies the inequation 3x + y ≤ 66000. So,the region which contains the origin represents the solution set of the inequation 3x + y ≤ 66000.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints x ≤ 20000, y ≤ 40000, x + y ≤ 45000, 3x + y ≤ 66000, x ≥ 0 and y ≥ 0 are as follows.
The corner points are O(0, 0), B1(0, 40000), G1(10500, 34500), H1(6000, 20000) and A1(20000, 0).
The values of Z at these corner points are as follows:
| Corner point | Z= 8x + 7y |
| O | 0 |
| B1 | 280000 |
| G1 | 325500 |
| H1 | 188000 |
| A1 | 160000 |
The maximum value of Z is 325500 which is attained at G1(10500, 34500).
Thus, the maximum profit is Rs 325500 obtained when 10500 bottles of A and 34500 bottles of B were manufactured.
Q30.
Answer :
Let x tickets of first class and y tickets of economy class were sold.
Number of tickets cannot be negative.
Therefore, x,y≥0
An aeroplane can carry a maximum of 200 passengers.
x+y≤200
The airline reserves at least 20 seats of first class and at least 4 times as many passengers prefer to travel by economy class to the first class.
x≥20y≥4x
A profit of Rs 400 is made on each first class ticket and a profit of Rs 600 is made on each economy class ticket.Therefore, profit gained by selling x tickets of first class and y tickets of economy class is Rs 400x and Rs 600y respectively.
Total profit = Z = 400x+600y which is to be maximised
Thus, the mathematical formulation of the given linear programmimg problem is
Max Z = 400x+600y
subject to
x+y≤200
x≥20y≥4x
x,y≥0
First we will convert inequations into equations as follows:
x + y =200, x = 20, y = 4x, x = 0 and y = 0
Region represented by x + y ≤ 200:
The line x + y = 200 meets the coordinate axes at A(200, 0) and B(0, 200) respectively. By joining these points we obtain the line
x + y = 200. Clearly (0,0) satisfies the inequation x + y ≤ 200. So,the region which contains the origin represents the solution set of the inequation x + y ≤ 200.
Region represented by x ≥ 20:
The line x = 20 is the line that passes through (20, 0) and is parallel to Y axis.The region to the right of the line x = 20 will satisfy the inequation x ≥ 20.
Region represented by y ≥ 4x:
The line y = 4x is the line that passes through (0, 0).The region above the line y = 4x will satisfy the inequation y ≥ 4x.Let us understand by taking one point which is below the line y = 4x. Let it be (1, 3).Here, 3 < 4 which does not satisfy the inequation y ≥ 4x.
Hence, the region above the line y = 4x will satisfy the inequation y ≥ 4x.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints x + y ≤ 200, x ≥ 20, y ≥ 4x, x ≥ 0 and y ≥ 0 are as follows.
The corner points are C(20, 80), D(40, 160), E(20, 180).
The values of Z at these corner points are as follows:
| Corner point | Z = 400x + 600y |
| C | 56000 |
| D | 112000 |
| E | 116000 |
The maximum value of Z is 116000 which is attained at C(20, 180).
Thus, the maximum profit is Rs 116000 obtained when 20 first class tickets and 180 economy class tickets were sold.
Q31.
Answer :
Let x kg of type I fertilizer and y kg of type II fertilizer are supplied.
Quantity of fertilizer cannot be negative.
Therefore, x,y≥0
A gardener has supply of fertilizer of type I which consists of 10% nitrogen and type II fertilizer consists of 5% nitrogen and he needs at least 14 kg of nitrogen for his crop.
10×100+5×100≥14⇒10x+5x≥1400
A gardener has supply of fertilizer of type I which consists 6% phosphoric acid and type II fertilizer consists of 10% phosphoric acid.
And he needs 14 kg of phosphoric acid for his crop.
6×100+10×100≥14⇒6x+10x≥1400
Therefore, according to the question, constraints are
10x+5y≥14006x+10y≥1400
If the type I fertilizer costs 60 paise per kg and type II fertilizer costs 40 paise per kg.Therefore, cost of x kg of type I fertilizer and y kg of type II fertilizer is Rs 0.60x and Rs 0.40y respectively.
Total cost = Z = 0.60x+0.40y which is to be minimised.
Thus, the mathematical formulation of the given linear programmimg problem is
Min Z = 0.60x+0.40y
subject to
6x+10y≥140010x+5y≥1400
x,y≥0
First we will convert inequations into equations as follows:
6x + 10y = 1400, 10x + 5y = 1400, x = 0 and y = 0
Region represented by 6x + 10y ≥ 1400:
The line 6x + 10y = 1400 meets the coordinate axes at A7003, 0 and B(0, 140) respectively. By joining these points we obtain the line
6x + 10y = 1400. Clearly (0,0) does not satisfies the 6x + 10y = 1400. So, the region which does not contain the origin represents the solution set of the inequation 6x + 10y ≥1400.
Region represented by 10x + 5y ≥ 1400:
The line 10x + 5y = 1400 meets the coordinate axes at C(140, 0) and D0, 280 respectively. By joining these points we obtain the line
10x + 5y = 1400. Clearly (0,0) does not satisfies the inequation 10x + 5y ≥ 1400. So,the region which does not contain the origin represents the solution set of the inequation 10x + 5y ≥ 1400.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints 6x + 10y ≥1400, 10x + 5y ≥ 1400, x ≥ 0 and y ≥ 0 are as follows.
The corner points are D(0, 280), E(100, 80) and A7003, 0.
The values of Z at these corner points are as follows:
| Corner point | Z= 0.60x + 0.40y |
| D | 112 |
| E | 92 |
| A | 140 |
The minimum value of Z is Rs 92 which is attained at E(100, 80).
Thus, the minimum cost is Rs 92 obtained when 100 kg of type I fertilizer and 80 kg of type II fertilizer were supplied.
Q32.
Answer :
Let Anil invests Rs x in Saving certificates and Rs y in National Saving bonds.
Therefore,
x,y≥0
Anil wants to invest at most Rs 12000 in Saving Certificates and National Saving Bonds.
x+y≤12000
According to rules, he has to invest at least Rs 2000 in Saving Certificates and at least Rs 4000 in National Saving Bonds.
x≥2000y≥4000
If the rate of interest on saving certificate is 8% per annum and the rate of interest on National Saving Bond is 10% per annum.
Total earning from investment = Z = 8×100+10y100 which is to be maximised.
Thus, the mathematical formulation of the given linear programmimg problem is
Max Z = 8×100+10y100
subject to
x+y≤12000x≥2000y≥4000
x,y≥0
First we will convert inequations into equations as follows:
x + y =12000, x = 2000, y = 4000, x = 0 and y = 0
Region represented by x + y ≤ 12000:
The line x + y = 12000 meets the coordinate axes at A(12000, 0) and B(0, 12000) respectively. By joining these points we obtain the line
x + y = 12000. Clearly (0,0) satisfies the inequation x + y ≤ 12000. So,the region which contains the origin represents the solution set of the inequation x + y ≤ 12000.
Region represented by x ≥ 2000:
The line x = 2000 is the line that passes through (2000, 0) and is parallel to Y axis.The region to the right of the line x = 2000 will satisfy the inequation x ≥ 2000.
Region represented by y ≥ 4000:
The line y = 4000 is the line that passes through (0, 4000) and is parallel to X axis.The region above the line y = 4000 will satisfy the inequation y ≥ 4000.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints is
The corner points are E(2000, 10000), D(8000, 4000), C(2000, 4000)
The values of Z at these corner points are as follows:
| Corner point | Z= 8×100+10y100 |
| E | 1160 |
| D | 1040 |
| C | 560 |
The maximum value of Z is 1160 which is attained at E(2000, 10000.
Thus, the maximum earning is Rs 1160 obtained when Rs 2000 were invested in Saving’s certificates and Rs 10000 were invested in National Saving Bond.
Q33.
Answer :
Let the man planted x trees of type A and y trees of type B.
Number of trees cannot be negative.
Therefore, x,y≥0
To plant tree of type A requires 10 sq.m and type B requires 20 sq.m of ground per tree. And, it is given that a man owns a field of area 1000 sq.m.Therefore,
10x+20y≤1000
Type A costs Rs 20 per tree and type B costs Rs 25 per tree.Therefore, x trees of type A and y trees of type B costs Rs 20x and Rs 25y respectively. A man has a sum of Rs 1400 to purchase young trees.
20x+25y≤1400
Thus, the mathematical formulation of the given linear programmimg problem is
Max Z = 40x − 20x + 60y − 25y = 20x + 35y
subject to
10x+20y≤100020x+25y≤1400
The feasible region determined by the system of constraints is
The corner points are A(0, 50), B(20, 40), C(70, 0)
The values of Z at these corner points are as follows:
| Corner point | Z = 20x + 35y |
| A | 1750 |
| B | 1800 |
| C | 1400 |
The maximum value of Z is 1800 which is attained at B(20, 40)
Thus, the maximum profit is Rs 1800 obtained when Rs 20 were invested on type A and Rs 40 were invested on type B.
Q34.
Answer :
Let the cottage industry manufacture x pedestal lamps and y wooden shades.
Number of lamps and wooden shades cannot be negative.
Therefore, x ≥ 0 and y ≥ 0
The given information can be compiled in a table as follows:
| Lamps | Shades | Availability | |
| Grinding/Cutting Machine (hr) | 2 | 1 | 12 |
| Sprayer (hr) | 3 | 2 | 20 |
Therefore, the constraints are:
The profit on a lamp is Rs 5 and on the shades is Rs 3.Therefore, profit on x pedestal lamps and y wooden shades is Rs 5x and Rs 3y respectively.
Total profit, Z = 5x + 3y
The mathematical formulation of the given problem is
Maximize Z = 5x + 3y
subject to the constraints,
x, y ≥ 0
First we will convert inequations into equations as follows:
2x + y =12, 3x + 2y = 20, x = 0 and y = 0
Region represented by 2x + y ≤ 12:
The line 2x + y = 12 meets the coordinate axes at A(6, 0) and B(0, 12) respectively. By joining these points we obtain the line
2x + y = 12. Clearly (0,0) satisfies the inequation 2x + y ≤ 12. So,the region which contains the origin represents the solution set of the inequation 2x + y ≤ 12.
Region represented by 3x + 2y ≤ 20:
The line 3x + 2y = 20 meets the coordinate axes at C203, 0 and D(0, 10) respectively. By joining these points we obtain the line
3x + 2y = 20. Clearly (0,0) satisfies the inequation 3x + 2y ≤ 20. So,the region which contains the origin represents the solution set of the inequation 3x + 2y ≤ 20.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints is as follows.
The corner points are O(0, 0), A(6, 0), E(4, 4), and D(0, 10).
The values of Z at these corner points are as follows:
| Corner point | Z = 5x + 3y |
| O | 0 |
| A | 30 |
| E | 32 |
| D | 30 |
The maximum value of Z is 32 at E(4, 4).
Thus, the manufacturer should produce 4 pedestal lamps and 4 wooden shades to maximize his profits.
Page 30.55 Ex.30.3
Q35.
Answer :
Let x1 and y1 units of goods x and y were produced respectively.
Number of units of goods cannot be negative.
Therefore, x1,y1≥0
To produce one unit of x, 2 units of labour and for one unit of y, 3 units of labour are required.
2×1+3y1≤30
To produce one unit of x, 3 units of capital is required and 1 unit of capital is required to produce one unit of y
3×1+y1≤17
If x and y are priced at Rs 100 and Rs 120 per unit respectively, Therefore, cost of x1 and y1 units of goods x and y is Rs 100×1 and Rs 120y1 respectively.
Total revenue = Z = 100×1+120y1 which is to be maximised.
Thus, the mathematical formulation of the given linear programmimg problem is
Max Z = 100×1+120y1
subject to
2×1+3y1≤303×1+y1≤17
x,y≥0
First we will convert inequations into equations as follows:
2×1 + 3y1 = 30, 3×1 + y1 = 17, x = 0 and y = 0
Region represented by 2×1 + 3y1 ≤ 30:
The line 2×1 + 3y1 = 30 meets the coordinate axes at A(15, 0) and B(0, 10) respectively. By joining these points we obtain the line
2×1 + 3y1 = 30. Clearly (0,0) satisfies the 2×1 + 3y1 = 30. So, the region which contains the origin represents the solution set of the inequation 2×1 + 3y1 ≤ 30.
Region represented by 3×1 + y1 ≤ 17:
The line 3×1 + y1 = 17 meets the coordinate axes at C173, 0 and D0, 17 respectively. By joining these points we obtain the line
3×1 + y1 = 17. Clearly (0,0) satisfies the inequation 3×1 + y1 ≤ 17. So,the region which contains the origin represents the solution set of the inequation 3×1 + y1 ≤ 17.
Region represented by x1 ≥ 0 and y1 ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints 2×1 + 3y1 ≤ 30, 3×1 + y1 ≤ 17, x ≥ 0 and y ≥ 0 are as follows.
The corner points are B(0, 10), E(3, 8) and C173, 0 .
The values of Z at these corner points are as follows
| Corner point | Z= 100×1+120y1 |
| B | 1200 |
| E | 1260 |
| C | 17003 |
The maximum value of Z is 1260 which is attained at E(3, 8).
Thus, the maximum revenue is Rs 1260 obtained when 3 units of x and 8 units of y were produced.
Q36.
Answer :
Let x units of product A and y units of product B were manufactured.
Number of products cannot be negative.
Therefore, x,y≥0
According to question, the given information can be tabulated as
| Time on M1(minutes) | Time on M2(minutes) | |
| Product A(x) | 1 | 2 |
| Product B(y) | 1 | 1 |
| Availability | 300 | 360 |
The constraints are
x+y≤300, 2x+y≤360
Firm manufactures two types of products A and B and sells them at a profit of Rs 5 per unit of type A and Rs 3 per unit of type B.Therefore, x units of product A and y units of product B costs Rs 5x and Rs 3y respectively.
Total profit = Z = 5x+3y which is to be maximised
Thus, the mathematical formulation of the given linear programmimg problem is
Max Z = 5x+3y
subject to
x+y≤300,
2x+y≤360
x,y≥0
First we will convert inequations into equations as follows:
x + y = 300, 2x + y = 360, x = 0 and y = 0
Region represented by x + y ≤ 300:
The line x + y = 300 meets the coordinate axes at A1(300, 0) and B1(0, 300) respectively. By joining these points we obtain the line
x + y = 30. Clearly (0,0) satisfies the x + y = 30. So, the region which contains the origin represents the solution set of the inequation
x + y ≤ 300.
Region represented by 2x + y ≤ 360:
The line 2x + y = 360 meets the coordinate axes at C1(180, 0) and D1(0, 360) respectively. By joining these points we obtain the line
2x + y = 360. Clearly (0,0) satisfies the inequation 2x + y ≤ 360. So,the region which contains the origin represents the solution set of the inequation 2x + y ≤ 360.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints x + y ≤ 300, 2x + y ≤ 360, x ≥ 0 and y ≥ 0 are as follows.
The corner points are O(0, 0), B1(0, 300), E1(60, 240) and C1(180, 0).
The values of Z at these corner points are as follows
| Corner point | Z= 5x + 3y |
| O | 0 |
| B1 | 900 |
| E1 | 1020 |
| C1 | 900 |
The maximum value of Z is Rs 1020 which is attained at B160, 240.
Thus, the maximum profit is Rs 1020 obtained when 60 units of product A and 240 units of product B were manufactured.
Q37.
Answer :
Let the firm manufacture x items of A and y items of B per day.
Number of items cannot be negative.
Therefore, x ≥0 and y ≥0.
It is given that the total number of items manufactured per day is at most 24.
∴ x + y ≤ 24
Item A takes 1 hour to make and item B takes 0.5 hour to make.
The maximum number of hours available per day is 16 hours.
∴ x + 0.5y ≤ 16
If the profit on one unit of item A be Rs 300 and one unit of item B be Rs 160.Therefore, profit gained on x items of A and y items of B is
Rs 300x and Rs 160y respectively.
∴ Total profit, Z = 300x + 160y
Thus, the mathematical formulation of the given problem is:
Maximise Z = 300x + 160y
subject to the constraints
x+ y ≤ 24
x + 0.5y ≤ 16
x, y ≥0
First we will convert inequations into equations as follows:
x + y = 24, x + 0.5y = 16, x = 0 and y = 0
Region represented by x + y ≤ 24:
The line x + y = 24 meets the coordinate axes at A1(24, 0) and B1(0, 24) respectively. By joining these points we obtain the line x + y = 24. Clearly (0,0) satisfies the x + y = 24. So, the region which contains the origin represents the solution set of the inequation
x + y ≤ 24.
Region represented by x + 0.5y ≤ 16:
The line x + 0.5y = 16 meets the coordinate axes at C1(16, 0) and D1(0, 32) respectively. By joining these points we obtain the line x + 0.5y = 16. Clearly (0,0) satisfies the inequation x + 0.5y ≤ 16. So,the region which contains the origin represents the solution set of the inequation x + 0.5y ≤ 16.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints x + y ≤ 24, x + 0.5y ≤ 16, x ≥ 0 and y ≥ 0 are as follows.
The corner points are O(0, 0) ,C1(16, 0), E1(8, 16) and B1(0, 24).
The value of Z at these corner points are as follows:
| Corner point | Z = 300x + 160y |
| O(0, 0) | 0 |
| C1(16, 0) | 4800 |
| E1(8, 16) | 4960 |
| B1(0, 24) | 3840 |
Thus, the maximum value of Z is 4960 at E1(8, 16).
Thus, 8 units of item A and 16 units of item B should be manufactured per day to maximise the profits.
Q38.
Answer :
Let x toys of type A and y toys of type B were manufactured.
The given information can be tabulated as follows:
| Cutting time (minutes) | Assembling time (minutes) | |
| Toy A(x) | 5 | 10 |
| Toy B(y) | 8 | 8 |
| Availability | 180 | 240 |
The constraints are
5x+8y≤18010x+8y≤240
The profit is Rs 50 each on type A and Rs 60 each on type B. Therefore, profit gained on x toys of type A and y toys of type B is Rs 50x and Rs 60 y respectively.
Total profit = Z = 50x+60y
The mathematical formulation of the given problem is
Max Z = 50x+60y
subject to
5x+8y≤18010x+8y≤240
First we will convert inequations into equations as follows:
5x + 8y = 180, 10x + 8y = 240, x = 0 and y = 0
Region represented by 5x + 8y ≤ 180:
The line 5x + 8y = 180 meets the coordinate axes at A1(36, 0) and B10, 452 respectively. By joining these points we obtain the line 5x + 8y = 180. Clearly, (0,0) satisfies the 5x + 8y = 180. So, the region which contains the origin represents the solution set of the inequation 5x + 8y ≤ 180.
Region represented by 10x + 8y ≤ 240:
The line 10x + 8y = 240 meets the coordinate axes at C1(24, 0) and D10, 30 respectively. By joining these points we obtain the line 10x + 8y = 240. Clearly (0,0) satisfies the inequation 10x + 8y ≤ 240. So,the region which contains the origin represents the solution set of the inequation 10x + 8y ≤ 240.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints 5x + 8y ≤ 180, 10x + 8y ≤ 240, x ≥ 0 and y ≥ 0 are as follows.
The feasible region is shown in the figure
The corner points are B10, 452, E1(12, 15) and C1(24, 0).
The values of Z at the corner points are
| Corner points | Z = 50x+60y |
| O | 0 |
| B1 | 1350 |
| E1 | 1500 |
| C1 | 1200 |
The maximum value of Z is 1500 which is at E1(12, 15).
Thus, for maximum profit, 12 units of toy A and 15 units of toy B should be manufactured.
Q39.
Answer :
Let x units and y units of articles A and B are produced respectively.
Number of articles cannot be negative.
Therefore, x,y≥0
The product of each unit of article A requires 4 hours in assembly and that of article B requires 2 hours in assembly and the maximum capacity of the assembly department is 60 hours a week
4x+2y≤60
The product of each unit of article A requires 2 hours in finishing and that of article B requires 4 hours in assembly and the maximum capacity of the finishing department is 48 hours a week.
2x+4y≤48
If the profit is Rs 6 for each unit of A and Rs 8 for each unit of B. Therefore, profit gained from x units and y units of articles A and B respectively is Rs 6x and Rs 8y respectively.
Total revenue = Z = 6x+8y which is to be maximised.
Thus, the mathematical formulation of the given linear programmimg problem is
Max Z = 6x+8y
subject to
2x+4y≤484x+2y≤60
x,y≥0
First we will convert inequations into equations as follows:
2x + 4y = 48, 4x + 2y = 60, x = 0 and y = 0
Region represented by 2x + 4y ≤ 48:
The line 2x + 4y = 48 meets the coordinate axes at A1(24, 0) and B10, 12 respectively. By joining these points we obtain the line 2x + 4y = 48. Clearly (0,0) satisfies the 2x + 4y = 48. So, the region which contains the origin represents the solution set of the inequation 2x + 4y ≤ 48.
Region represented by 4x + 2y ≤ 60:
The line 4x + 2y = 60 meets the coordinate axes at C1(15, 0) and D10, 30 respectively. By joining these points we obtain the line 4x + 2y = 60. Clearly (0,0) satisfies the inequation 4x + 2y ≤ 60. So,the region which contains the origin represents the solution set of the inequation 4x + 2y ≤ 60.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints 2x + 4y ≤ 48, 4x + 2y ≤ 60, x ≥ 0 and y ≥ 0 are as follows.
The corner points are O(0, 0), B1(0, 12), E1(12, 6) and C1(15,0).
The values of Z at these corner points are as follows
| Corner point | Z= 6x + 8y |
| O | 0 |
| B1 | 96 |
| E1 | 120 |
| C1 | 90 |
The maximum value of Z is 120 which is attained at E1(12, 6).
Thus, the maximum profit is Rs 120 obtained when 12 units of article A and 6 units of article B were manufactured.
Q40.
Answer :
Let x and y be the number of items of A and B that should be produced each day to maximize the profit.
Number of items cannot be negative.
Therefore,
It is also given that the firm can produce at most 24 items in a day.
∴ x+ y ≤ 24
Also, the time required to make an item of A is one hour and time required to make an item of B is half an hour.
Therefore, the time required to produce x items of A and y items of B is hours. However, the maximum time available in a day is 16 hours.
It is given that the profit on an item of A is Rs 300 and on one item of B is Rs 160. Therefore, the profit gained from x items of A and y items of B is Rs 300x and Rs 160y respectively.
Total profit Z = 300x + 160y
The mathematical form of the given LPP is:
Maximize Z = 300x + 160y
subject to constraints:
x+y≤24x+12y≤16x≥0, y≥0
First we will convert inequations into equations as follows:
x + y = 24, x + 12y = 16, x = 0 and y = 0
Region represented by x + y ≤ 24:
The line x + y = 24 meets the coordinate axes at A1(24, 0) and B10, 24 respectively. By joining these points we obtain the line x + y = 24. Clearly, (0,0) satisfies the x + y = 24. So, the region which contains the origin represents the solution set of the inequation x + y ≤ 24.
Region represented by x + 12y ≤ 16:
The line x + 12y = 16 meets the coordinate axes at C1(16, 0) and D10, 32 respectively. By joining these points we obtain the line x + 12y = 16. Clearly, (0,0) satisfies the inequation x + 12y ≤ 16. So,the region which contains the origin represents the solution set of the inequation x + 12y ≤ 16.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints x + y ≤ 24, x + 12y ≤ 16, x ≥ 0 and y ≥ 0 are as follows.
The feasible region is shown in the figure
GRAPH
In the above graph, the shaded region is the feasible region. The corner points are O(0, 0), C1(16, 0), E1(8, 16), and B1(0, 24).
The values of the objective function Z at corner points of the feasible region are given in the following table:
Corner Points | Z = 300x + 160y | |
O(0, 0) | 0 | |
C1(16, 0) | 4800 | |
E1(8, 16) | 4960 | Maximum |
B1(0, 24) | 3840 |
Clearly, Z is maximum at x = 8 and y = 16 and the maximum value of Z at this point is 4960.
Thus, 8 items of A and 16 items of B should be produced in order to maximize the profit and the maximum profit is Rs 4960.
Q41.
Answer :
Let x units of product A and y units of product B were manufactured.
Clearly, x≥0, y≥0
It takes 5 hours to produce a unit of A and 3 hours to produce a unit of B.The two products are produced in a common production process, which has a total capacity of 500 man-hours.
5x+3y≤500
The maximum number of unit of A that can be sold is 70 and that for B is 125.
x≤70y≤125
If the profit is Rs 20 per unit for the product A and Rs 15 per unit for the product B. Therefore, profit x units of product A and y units of product B is Rs 20x and Rs 15y respectively.
Total profit = Z = 20x+15y
The mathematical formulation of the given problem is
Max Z = 20x+15y
subject to
5x+3y≤500x≤70y≤125
x≥0, y≥0
First we will convert inequations into equations as follows:
5x + 3y = 500, x = 70, y = 125, x = 0 and y = 0
Region represented by 5x + 3y ≤ 500:
The line 5x + 3y = 500 meets the coordinate axes at A1(100, 0) and B10,5003 respectively. By joining these points we obtain the line 5x + 3y = 500. Clearly (0,0) satisfies the 5x + 3y = 500. So, the region which contains the origin represents the solution set of the inequation 5x + 3y ≤ 500.
Region represented by x ≤ 70:
The line x = 70 is the line passes through C1(70, 0) and is parallel to Y axis. The region to the left of the line x = 70 will satisfy the inequation x ≤ 70.
Region represented by y ≤ 125:
The line y = 125 is the line passes through D1(0, 125) and is parallel to X axis. The region below the the line y = 125 will satisfy the inequation y ≤ 125.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints 5x + 3y ≤ 500, x ≤ 70, y ≤ 125, x ≥ 0 and y ≥ 0 are as follows.
The corner points are O(0, 0), D10, 125, E1(25, 125), F1(70, 50) and C1(70, 0).
The values of Z at the corner points are
| Corner points | Z = 20x+15y |
| O | 0 |
| D1 | 1875 |
| E1 | 2375 |
| F1 | 2150 |
| C1 | 1400 |
The maximum value of Z is 2375 which is at E125, 125.
Thus, maximum profit is Rs 2375, 25 units of A and 125 units of B should be manufactured.
Q42.
Answer :
Let x large boxes and y small boxes be manufactured.
Number of boxes cannot be negative.
Therefore, x≥0, y≥0
The large boxes require 4 sq. metre per box while the small boxes require 3 sq. metre per box and if 60 sq. metre of cardboard is in stock.
4x+3y≤60
The manufacturer is required to make at least three large boxes and at least twice as many small boxes as large boxes.
x≥3y≥2x
If the profits on the large and small boxes are Rs 3 and Rs 2 per box. Therefore, profit gained by him on x large boxes and y small boxes is Rs 3x and Rs 2y respectively.
Total profit = Z = 3x+2y
The mathematical formulation of the given problem is
Max Z = 3x+2y
subject to
4x+3y≤60x≥3y≥2x
x≥0, y≥0
First we will convert inequations into equations as follows:
4x + 3y = 60, x = 3, y = 2x, x = 0 and y = 0
Region represented by 4x + 3y ≤ 60:
The line 4x + 3y = 60 meets the coordinate axes at A(15, 0) and B(0, 20) respectively. By joining these points we obtain the line
4x + 3y = 60. Clearly (0,0) satisfies the 4x + 3y = 60. So, the region which contains the origin represents the solution set of the inequation 4x + 3y ≤ 60.
Region represented by x ≥ 3:
The line x = 3 is the line passes through (3, 0) and is parallel to Y axis. The region to the right of the line x = 3 will satisfy the inequation
x ≥ 3.
Region represented by y ≥ 2x:
The line y = 2x is the line that passes through (0, 0). The region above the line y = 2x will satisfy the inequation y ≥ 2x. Like if we take an example taking a point (5, 1) below the line y = 2x .Here, 1 < 10 which does not satisfies the inequation y ≥ 2x. Hence, the region above the line y = 2x will satisfy the inequation y ≥ 2x.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints 4x + 3y ≤ 60, x ≥ 3, y ≥ 2x, x ≥ 0 and y ≥ 0 are as follows
The corner points are E3, 16, D(6, 12) and C(3, 6).
The values of Z at the corner points are
| Corner points | Z = 3x+2y |
| E | 41 |
| D | 42 |
| C | 21 |
The maximum value of Z is 42 which is at D6, 12.
Thus, for maximum profit is Rs 42, 6 units of large boxes and 12 units of smaller boxes should be manufactured.
Q43.
Answer :
Let x units of product A and y units of product B were manufactured.
Number of units cannot be negative.
Therefore, x,y≥0
According to question, the given information can be tabulated as:
| Selling price(Rs) | Manufacturing time(hrs) | |
| Product A(x) | 200 | 0.5 |
| Product B(y) | 300 | 1 |
Also, the availability of time is 40 hours and the revenue should be atleast Rs 10000.
Further, it is given that there is a permanent order for 14 units of product A and 16 units of product B.
Therefore, the constraints are
200x+300y≥100000.5x+y≤40x≥14y≥16
If the profit on each of product A is Rs 20 and on product B is Rs 30.Therefore, profit gained on x units of product A and y units of product B is Rs 20x and Rs 30y respectively.
Total profit = Z = 20x+30y which is to be maximised
Thus, the mathematical formulation of the given linear programmimg problem is
Max Z = 20x+30y
subject to
2x+3y≥100x+2y≤80x≥14y≥16
x,y≥0
First we will convert inequations into equations as follows:
2x + 3y = 100, x + 2y = 80, x = 14, y = 16, x = 0 and y = 0.
Region represented by 2x + 3y ≥ 100:
The line 2x + 3y = 100 meets the coordinate axes at A1(50, 0) and B10, 1003 respectively. By joining these points we obtain the line
2x + 3y = 100 . Clearly (0,0) does not satisfies the 2x + 3y = 100. So, the region which does not contain the origin represents the solution set of the inequation 2x + 3y ≥ 100.
Region represented by x + 2y ≤ 80:
The line x + 2y = 80 meets the coordinate axes at C1(80, 0) and D1(0, 40) respectively. By joining these points we obtain the line
x + 2y = 80. Clearly (0,0) satisfies the inequation x + 2y ≤ 80. So,the region which contains the origin represents the solution set of the inequation x + 2y ≤ 80.
Region represented by x ≥ 14
x = 14 is the line passes through (14, 0) and is parallel to the Y axis.The region to the right of the line x = 14 will satisfy the inequation.
Region represented by y ≥ 16
y = 16 is the line passes through (0, 16) and is parallel to the X axis.The region above the line y = 16 will satisfy the inequation.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints 2x + 3y ≥ 100, x + 2y ≤ 80, x ≥ 14, y ≥ 16, x ≥ 0 and y ≥ 0 are as follows.
The corner points of the feasible region are E1(26, 16), F1(48, 16), G1(14, 33) and H1(14, 24)
The values of Z at these corner points are as follows
| Corner point | Z= 20x + 30y |
| E1 | 1000 |
| F1 | 1440 |
| G1 | 1270 |
| H1 | 1000 |
The maximum value of Z is Rs 1440 which is attained at F148, 16.
Thus, the maximum profit is Rs 1440 obtained when 48 units of product A and 16 units of product B were manufactured.
Page 30.56 Ex.30.3
Q44.
Answer :
Let young man drives x km at a speed of 25 km/hr and y km at a speed of 40 km/hr.
Clearly, x,y≥0
It is given that, he spends Rs 2 per km if he drives at a speed of 25 km/hr and Rs 5 per km if he drives at a speed of 40 km/hr. Therefore, money spent by him when he travelled x km and y km is Rs 2x and Rs 5y respectively.
It is given that he has a maximum of Rs 100 to spend.
Thus, 2x+5y≤100
Time spent by him when travelling with a speed of 25 km/hr =x25hrTime spent by him when travelling with a speed of 40 km/hr =x40hr
Also, the available time is of 1 hour.
x25+y40≤1⇒40x+25y≤1000
The distance covered is Z = x+y which is to be maximised.
Thus, the mathematical formulation of the given linear programmimg problem is
Max Z = x+y
subject to
2x+5y≤10040x+25y≤1000
x,y≥0
First we will convert inequations into equations as follows:
2x + 5y = 100, 40x + 25y = 1000, x = 0 and y = 0
Region represented by 2x + 5y ≤ 100:
The line 2x + 5y = 100 meets the coordinate axes at A50, 0 and B0, 20 respectively. By joining these points we obtain the line
2x + 5y = 100. Clearly (0,0) satisfies the 2x + 5y = 100. So,the region which contains the origin represents the solution set of the inequation 2x + 5y ≤ 100.
Region represented by 40x + 25y ≤ 1000:
The line 40x + 25y = 1000 meets the coordinate axes at C25, 0 and D0, 40 respectively. By joining these points we obtain the line
2x + y = 12.Clearly (0,0) satisfies the inequation 40x + 25y ≤ 1000. So,the region which contains the origin represents the solution set of the inequation 40x + 25y ≤ 1000.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints 2x + 5y ≤ 100, 40x + 25y ≤ 1000, x ≥ 0, and y ≥ 0 are as follows
The corner points are O(0, 0), B(0, 20), E503, 403 and C(25, 0).
The values of Z at these corner points are as follows
| Corner point | Z = x + y |
| O | 0 |
| B | 20 |
| E | 30 |
| C | 25 |
The maximum value of Z is 30 which is attained at E.
Thus, the maximum distance travelled by the young man is 30 kms, if he drives 503 km at a speed of 25 km/hr and 403km at a speed of 40 km/hr .
Q45.
Answer :
Let x and y litres of oil be supplied from A to the petrol pumps D and E. Then, (7000 − x − y) L will be supplied from A to petrol pump F.
The requirement at petrol pump D is 4500 L. Since, x L are transported from depot A, the remaining (4500 −x) L will be transported from petrol pump B.
Similarly, (3000 − y) L and [3500 − (7000 − x − y)] L i.e. (x + y − 3500) L will be transported from depot B to petrol pump E and F. respectively.
The given problem can be represented diagrammatically as follows.
Since, quantity of oil are non-negative quantities.Therefore,
Cost of transporting 10 L of petrol = Re 1
Cost of transporting 1 L of petrol = Rs 110
Therefore, total transportation cost is given by,
The problem can be formulated as follows.
Minimize Z = 0.3x + 0.1y + 3950
subject to the constraints,
x+y≤7000x≤4500y≤3000x+y≥3500x, y≥0
First we will convert inequations into equations as follows:
x + y = 7000, x = 4500, y = 3000, x + y = 3500, x = 0 and y = 0
Region represented by x + y ≤ 7000:
The line x + y = 7000 meets the coordinate axes at A1(7000, 0) and B10, 7000 respectively. By joining these points we obtain the line
x + y = 7000 . Clearly (0,0) satisfies the x + y = 7000 . So, the region which contains the origin represents the solution set of the inequation x + y ≤ 7000.
Region represented by x ≤ 4500:
The line x = 4500 is the line passes through C1(4500, 0) and is parallel to Y axis. The region to the left of the line x = 4500 will satisfy the inequation
x ≤ 4500.
Region represented by y ≤ 3000:
The line y = 3000 is the line passes through D1(0, 3000) and is parallel to X axis. The region below the the line y = 3000 will satisfy the inequation
y ≤ 3000.
Region represented by x + y ≥ 3500:
The line x + y = 7000 meets the coordinate axes at E1(3500, 0) and F10, 3500 respectively. By joining these points we obtain the line
x + y = 3500 . Clearly (0,0) satisfies the x + y = 3500. So, the region which contains the origin represents the solution set of the inequation x + y ≥ 3500.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints x + y ≤ 7000, x ≤ 4500, y ≤ 3000, x + y ≥ 3500, x ≥ 0 and y ≥ 0 are as follows.
The corner points of the feasible region are E1(3500, 0), C1(4500, 0), I1(4500, 2500), H1(4000, 3000), and G1(500, 3000).
The values of Z at these corner points are as follows
| Corner point | Z = 0.3x + 0.1y + 3950 |
| E1(3500, 0) | 5000 |
| C1(4500, 0) | 5300 |
| I1(4500, 2500) | 5550 |
| H1(4000, 3000) | 5450 |
| G1(500, 3000) | 4400 |
The minimum value of Z is 4400 at G1(500, 3000).
Thus, the oil supplied from depot A is 500 L, 3000 L, and 3500 L and from depot B is 4000 L, 0 L, and 0 L to petrol pumps D, E, and F respectively.
The minimum transportation cost is Rs 4400.
Q46.
Answer :
Let the firm manufacture x gold rings and y chains per day.
Number of gold rings and chains cannot be negative.
Therefore, x ≥0 and y ≥0.
It is given that the total number of gold rings and chains manufactured per day is at most 24.
∴ x + y ≤ 24
The gold ring takes 1 hour to make and chain takes 30 min, that is, 0.5 hour to make.
The maximum number of hours available per day is 16 hours.
∴ x + 0.5y ≤ 16
The profit on a ring is Rs 300 and on a chain is Rs 190. Therefore, profit made from x gold rings and y chains is Rs 300x and Rs 190y respectively.
∴ Total profit, Z = 300x + 190y
Thus, the mathematical formulation of the given problem is:
Maximise Z = 300x + 190y
subject to the constraints
x + y ≤ 24
x + 0.5y ≤ 16
x, y ≥0
First we will convert inequations into equations as follows:
x + y = 24, x + 0.5y = 16, x = 0 and y = 0
Region represented by x + y ≤ 24:
The line x + y = 24 meets the coordinate axes at A(24, 0) and B0, 24 respectively. By joining these points we obtain the line x + y = 24. Clearly (0,0) satisfies the x + y = 24. So, the region which contains the origin represents the solution set of the inequation
x + y ≤ 24.
Region represented by x + 0.5y ≤ 16:
The line x + 0.5y = 16 meets the coordinate axes at C(16, 0) and D0, 32 respectively. By joining these points we obtain the line x + 0.5y = 16. Clearly (0,0) satisfies the inequation x + 0.5y ≤ 16. So,the region which contains the origin represents the solution set of the inequation x + 0.5y ≤ 16.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints x + y ≤ 24, x + 0.5y ≤ 16, x ≥ 0 and y ≥ 0 are as follows.
The feasible region determined by the system constraints is as follows:
The corner points are O(0, 0), C(16, 0), E(8, 16) and B(0, 24).
The value of Z at these corner points are as follows:
| Corner point | Z = 300x + 190y |
| O(0, 0) | 0 |
| C(16, 0) | 4800 |
| E(8, 16) | 5440 |
| B(0, 24) | 4560 |
Thus, the maximum value of Z is 5440 at E(8, 16).
Thus, 8 gold rings and 16 chains should be manufactured per day to maximise the profits.
Q47.
Answer :
Let x books of first type and y books of second type were accommodated.
Number of books cannot be negative.
Therefore, x,y≥0
According to question, the given information can be tabulated as:
| Thickness(cm) | Weight(kg) | |
| First type(x) | 6 | 1 |
| Second type(y) | 4 | 1.5 |
| Capacity of shelf | 96 | 21 |
Therefore, the constraints are
6x+4y≤96x+1.5y≤21
Number of books = Z = x+y which is to be maximised
Thus, the mathematical formulation of the given linear programmimg problem is
MaxImize Z = x+y
subject to
6x+4y≤96x+1.5y≤21
First we will convert inequations into equations as follows:
6x + 4y = 96, x + 1.5y = 21, x = 0 and y = 0
Region represented by 6x + 4y ≤ 96:
The line 6x + 4y = 96 meets the coordinate axes at A(16, 0) and B0, 24 respectively. By joining these points we obtain the line
6x + 4y = 96. Clearly (0,0) satisfies the 6x + 4y = 96. So, the region which contains the origin represents the solution set of the inequation
6x + 4y ≤ 96.
Region represented by x + 1.5y ≤ 21:
The line x + 1.5y = 21 meets the coordinate axes at C(21, 0) and D0, 14 respectively. By joining these points we obtain the line
x + 1.5y = 21. Clearly (0,0) satisfies the inequation x + 1.5y ≤ 21. So,the region which contains the origin represents the solution set of the inequation x + 1.5y ≤ 21.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints 6x + 4y ≤ 96, x + 1.5y ≤ 21, x ≥ 0 and y ≥ 0 are as follows.
The corner points are O(0, 0), D(0, 14), E(12, 6), A(16, 0)
The values of Z at these corner points are as follows
| Corner point | Z= x + y |
| O | 0 |
| D | 14 |
| E | 18 |
| A | 16 |
The maximum value of Z is 18 which is attained at E12, 6.
Thus, maximum number of books that can be arranged on shelf is 18 where 12 books are of first type and 6 books are the other type.
Q48.
Answer :
Let there be x cakes of first kind and y cakes of second kind.
∴ x ≥ 0 and y ≥ 0
The given information can be compiled in the form of a table as:
| Flour (gm) | Fat (gm) | |
| Cakes of first kind | 300 | 15 |
| Cakes of second kind | 150 | 30 |
| Availability | 7500 | 600 |
Therefore, constraints are:
300x+150y≤750015x+30y≤600
Total number of cakes that can be made = Z = x + y
Thus, the given problem can be mathematically formulated as:
Maximize Z = x + y
subject to constraints,
300x+150y≤750015x+30y≤600
x, y ≥ 0
First we will convert inequations into equations as follows:
300x + 150y = 7500, 15x + 30y = 600, x = 0 and y = 0
Region represented by 300x + 150y ≤ 7500:
The line 300x + 150y = 7500 meets the coordinate axes at A(25, 0) and B0, 50 respectively. By joining these points we obtain the line
300x + 150y = 7500. Clearly (0,0) satisfies the 300x + 150y = 7500. So, the region which contains the origin represents the solution set of the inequation 300x + 150y ≤ 7500.
Region represented by 15x + 30y ≤ 600:
The line 15x + 30y = 600 meets the coordinate axes at C(40, 0) and D0, 20 respectively. By joining these points we obtain the line
15x + 30y = 600. Clearly (0,0) satisfies the inequation 15x + 30y ≤ 600. So,the region which contains the origin represents the solution set of the inequation 15x + 30y ≤ 600.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints 300x + 150y ≤ 7500, 15x + 30y ≤ 600, x ≥ 0 and y ≥ 0 are as follows.
The corner points are O(0, 0), A(25, 0), E(20, 10) and D(0, 20).
The values of Z at these corner points are:
| Corner points | Z = x + y |
| O(0, 0) | 0 |
| A(25, 0) | 25 |
| E(20, 10) | 30 |
| D(0, 20) | 20 |
Thus, maximum numbers of cakes that can be made from 20 of the first kind and 10 of the other kind.
Q49.
Answer :
Let x number of tennis rackets and y number of cricket bats were sold.
Number of tennis rackets and cricket balls cannot be negative.
Therefore, x≥0, y≥0
It is given that a tennis racket takes 1.5 hours of machine time and 3 hours of craftman’s time in its making while a cricket bat takes 3 hours of machine time and 1 hour of craftman’s time.
Also, the factory has the availability of not more than 42 hours of machine time and 24 hours of craftman’s time.Therefore,
1.5 x plus 3 y less or equal than 42
3 x plus y less or equal than 24
If the profit on a racket and on a bat is Rs 20 and Rs 10 respectively.Therefore, profit made on x tennis rackets and y cricket bats is Rs 20x and Rs 10y respectively.
Total profit = Z = 20x + 10y
The mathematical form of the given LPP is:
Maximize Z = 20x + 10y
Subject to constraints:
1.5 x plus 3 y less or equal than 42
3 x plus y less or equal than 24
x≥0, y≥0
First we will convert inequations into equations as follows:
1.5x + 3y = 42, 3x + y = 24, x = 0 and y = 0
Region represented by 1.5x + 3y ≤ 42:
The line 1.5x + 3y = 42 meets the coordinate axes at A1(28, 0) and B10, 14 respectively. By joining these points we obtain the line 1.5x + 3y = 42. Clearly (0,0) satisfies the 1.5x + 3y = 42. So, the region which contains the origin represents the solution set of the inequation 1.5x + 3y ≤ 42.
Region represented by 3x + y ≤ 24:
The line 3x + y = 24 meets the coordinate axes at C1(8, 0) and D10, 24 respectively. By joining these points we obtain the line 3x + y = 24. Clearly (0,0) satisfies the inequation 3x + y ≤ 24. So,the region which contains the origin represents the solution set of the inequation 3x + y ≤ 24.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints 1.5x + 3y ≤ 42, 3x + y ≤ 24, x ≥ 0 and y ≥ 0 are as follows.
In the above graph, the shaded region is the feasible region.
The corner points are O(0, 0), B1(0, 14), E1(4, 12), and C1(8, 0).
The values of the objective function Z at corner points of the feasible region are given in the following table:
| Corner Points | Z = 20x +10y | |
| O(0, 0) | 0 | |
| B1(0, 14) | 140 | |
| E1(4, 12) | 200 | Maximum |
| C1(8, 0) | 160 |
Clearly, Z is maximum at x = 4 and y = 12 and the maximum value of Z at this point is 200.
Thus, maximum profit is of Rs 200 obtained when 4 tennis rackets and 12 cricket bats were sold.
Q50.
Answer :
Let x and y be the number of desktop model and portable model respectively.
Number of desktop model and portable model cannot be negative.
Therefore,
It is given that the monthly demand will not exist 250 units.
∴ x+y≤250
Cost of desktop and portable model is Rs 25,000 and Rs 40,000 respectively. Therefore, cost of x desktop model and y portable model is Rs 25,000 and Rs 40,000 respectively and he does not want to invest more than Rs 70 lakhs.
25000x+40000y≤7000000
Profit on the desktop model is Rs 4500 and on the portable model is Rs 5000. Therefore, profit made by x desktop model and y portable model is Rs 4500x and Rs 5000y respectively.
Total profit = Z = 4500x + 5000y
The mathematical form of the given LPP is:
Maximize Z = 4500x + 5000y
Subject to constraints:
x+y≤250
25000x+40000y≤7000000
First we will convert inequations into equations as follows:
x + y = 250, 25000x + 40000y = 7000000, x = 0 and y = 0
Region represented by x + y ≤ 250:
The line x + y = 250 meets the coordinate axes at A(250, 0) and B0, 250 respectively. By joining these points we obtain the line
x + y = 250. Clearly (0,0) satisfies the x + y = 250. So, the region which contains the origin represents the solution set of the inequation x + y ≤ 250.
Region represented by 25000x + 40000y ≤ 7000000:
The line 25000x + 40000y = 7000000 meets the coordinate axes at C(280, 0) and D0, 175 respectively. By joining these points we obtain the line 25000x + 40000y = 7000000. Clearly (0,0) satisfies the inequation 25000x + 40000y ≤ 7000000. So,the region which contains the origin represents the solution set of the inequation 25000x + 40000y ≤ 7000000.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints x + y ≤ 250, 25000x + 40000y ≤ 7000000, x ≥ 0 and y ≥ 0 are as follows.
The corner points are O(0, 0), D(0, 175), E(200, 50) and A(250, 0).
The values of the objective function Z at corner points of the feasible region are given in the following table:
Corner Points | Z = 4500x + 5000y | |
| O(0, 0) | 0 | |
D(0, 175) | 875000 | |
E(200, 50) | 1150000 | Maximum |
A(250, 0) | 1125000 |
Clearly, Z is maximum at x = 200 and y = 50 and the maximum value of Z at this point is 1150000.
Thus, 200 desktop models and 50 portable units should be sold to maximize the profit.
Q51.
Answer :
Let godown A supply x quintals and y quintals of grain to the shops D and E respectively.
Then, (100 − x − y) will be supplied to shop F.
The requirement at shop D is 60 quintals since, x quintals are transported from godown A.
Therefore, the remaining (60 − x) quintals will be transported from godown B.
Similarly, (50 − y) quintals and 40 − (100 − x − y) i.e. (x + y − 60) quintals will be transported from godown B to shop E and F respectively.
The given problem can be represented diagrammatically as follows.
Quantity of the grain cannot be negative.Therefore,
Total transportation cost Z is given by,
Z=6x+3y+2.5100-x-y+460-x+250-y+3x+y-60 =6x+3y+250-2.5x-2.5y+240-4x+100-2y+3x+3y-180 =2.5x+1.5y+410
The given problem can be formulated as:
Minimize Z = 2.5x + 1.5y + 410
subject to the constraints,
x+y≤100x≤60y≤50x+y≥60x, y≥0
First we will convert inequations into equations as follows:
x + y = 100, x = 60, y = 50, x + y =60, x = 0 and y = 0
Region represented by x + y ≤ 100:
The line x + y = 100 meets the coordinate axes at A1(100, 0) and B1(0, 100) respectively. By joining these points we obtain the line x + y = 100. Clearly (0,0) satisfies the x + y = 100. So, the region which contains the origin represents the solution set of the inequation x + y ≤ 100.
Region represented by x ≤ 60:
x = 60 is the line that passes (60, 0) and is parallel to the Y axis.The region to the left of the line x = 60 will satisfy the inequation x ≤ 60.
Region represented by y ≤ 50:
y = 50 is the line that passes (0, 50) and is parallel to the X axis.The region below the line y = 50 will satisfy the inequation y ≤ 50.
Region represented by x + y ≥ 60:
The line x + y = 60 meets the coordinate axes at C1(60, 0) and D10, 60 respectively. By joining these points we obtain the line x + y = 60. Clearly (0,0) does not satisfies the inequation x + y ≥ 60. So,the region which does not contain the origin represents the solution set of the inequation x + y ≥ 60.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints x + y ≤ 100, x ≤ 60, y ≤ 50, x + y ≥ 60, x ≥ 0 and y ≥ 0 are as follows.
The corner points are C1(60, 0), G1(60, 40), F1(50, 50), and E1(10, 50).
The values of Z at these corner points are as follows.
| Corner point | Z = 2.5x + 1.5y + 410 |
| C1(60, 0) | 560 |
| G1(60, 40) | 620 |
| F1(50, 50) | 610 |
| E1(10, 50) | 510 |
The minimum value of Z is 510 at E1(10, 50).
Thus, the amount of grain transported from A to D, E, and F is 10 quintals, 50 quintals, and 40 quintals respectively and from B to D, E, and F is 50 quintals, 0 quintals, and 0 quintals respectively.
The minimum cost is Rs 510.
Page 30.57 Ex.30.3
Q52.
Answer :
Let x and y packets be transported from factory A to the agencies P and Q respectively. Then, [60 − (x + y)] packets be transported to the agency R.
The requirement at agency P is 40 packets. Since, x packets are transported from factory A,
Therefore, the remaining (40 − x) packets are transported from factory B.
Similarly, (40 − y) packets are transported by B to Q and 50− [60 − (x + y)] i.e. (x + y − 10) packets will be transported from factory B to agency R respectively.
Number of packets cannot be negative.Therefore,
x≥0, y≥0 and 60-x-y≥0⇒x≥0, y≥0 and x+y≤6040-x≥0, 40-y≥0 and x+y-10≥0⇒x≤ 40, y≤40 and x+y≥10
Total transportation cost Z is given by,
Z=5x+4y+360-x+y+440-x+240-y+5x+y-10 =3x+4y+10
Minimize Z = 5x+4y+360-x-y+440-x+240-y+5x+y-10
=3x+4y+370
subject to
x+y≤60x≤40y≤40x+y≥10x, y≥0
First we will convert inequations into equations as follows:
x + y = 60, x = 40, y = 40, x + y = 10, x = 0 and y = 0
Region represented by x + y ≤ 60:
The line x + y = 60 meets the coordinate axes at A1(60, 0) and B1(0, 60) respectively. By joining these points we obtain the line
x + y = 60. Clearly (0,0) satisfies the x + y = 60. So, the region which contains the origin represents the solution set of the inequation
x + y ≤ 60.
Region represented by x ≤ 40:
x = 40 is the line that passes C1(40, 0) and is parallel to the Y axis.The region to the left of the line x = 40 will satisfy the inequation x ≤ 40.
Region represented by y ≤ 40:
y = 40 is the line that passes D1(0, 40) and is parallel to the X axis.The region below the line y = 40 will satisfy the inequation y ≤ 40.
Region represented by x + y ≥ 10:
The line x + y = 10 meets the coordinate axes at E1(10, 0) and F10, 10 respectively. By joining these points we obtain the line x + y = 10. Clearly (0,0) does not satisfies the inequation x + y ≥ 10. So,the region which does not contain the origin represents the solution set of the inequation x + y ≥ 10.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints x + y ≤ 60, x ≤ 40, y ≤ 40, x + y ≥ 10, x ≥ 0 and y ≥ 0 are as follows.
The corner points are D1(0, 40), H1(20, 40), G1(40, 20), C1(40, 0), E1(10, 0) and F1(0, 10).
The values of Z at these corner points are as follows
| Corner point | Z= 3x + 4y + 370 |
| D1 | 530 |
| H1 | 590 |
| G1 | 570 |
| C1 | 490 |
| E1 | 400 |
| F1 | 410 |
The minimum value of Z is 400 which is at E1(10, 0).
Thus, the minimum cost is Rs 400.
Hence,
From A: 10 packets, 0 packets and 50 packets to P, Q and R respectively
From B: 30 packets, 40 packets and 0 packets to P, Q and R respectively
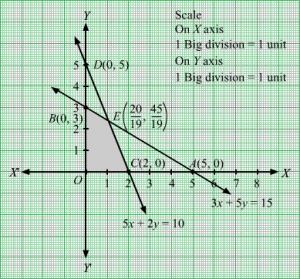
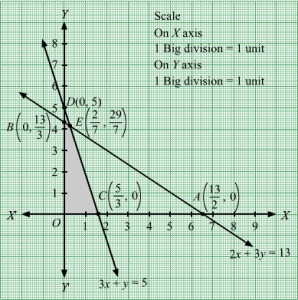
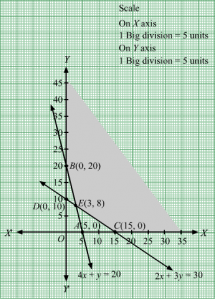
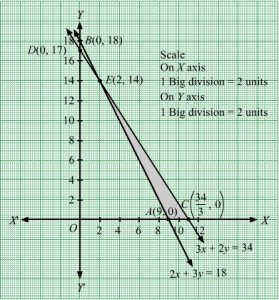
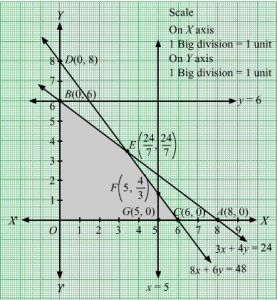
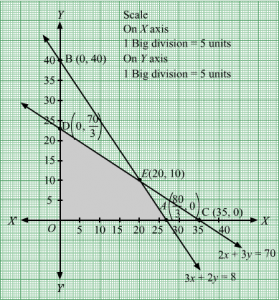
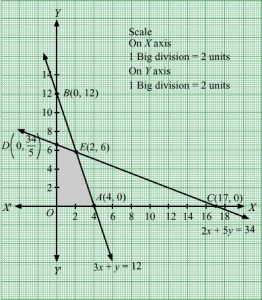
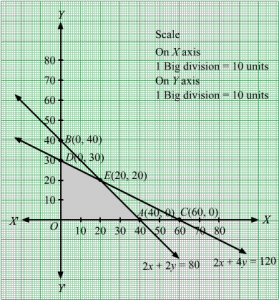
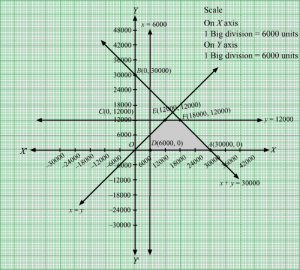
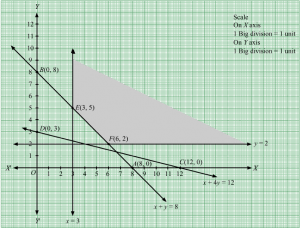
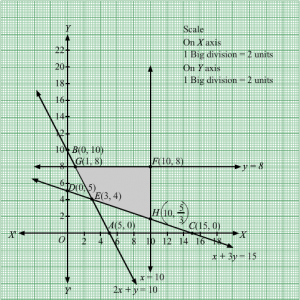

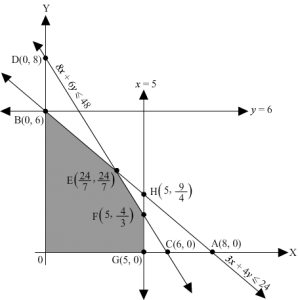
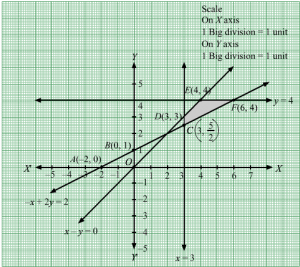
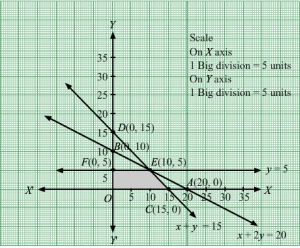
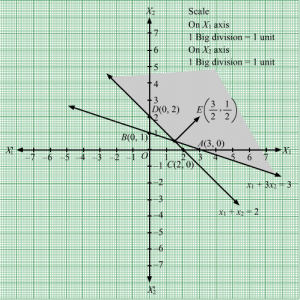
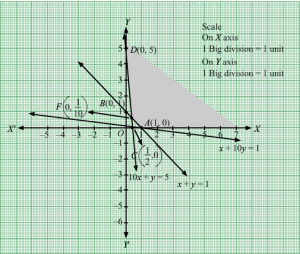
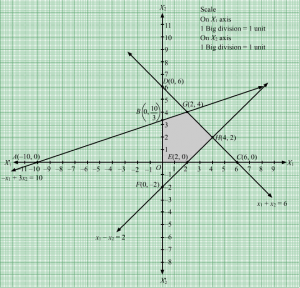
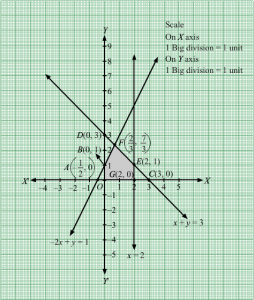
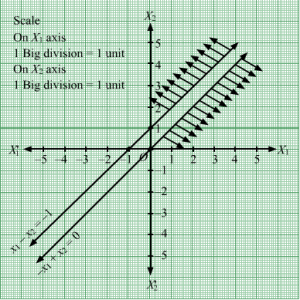
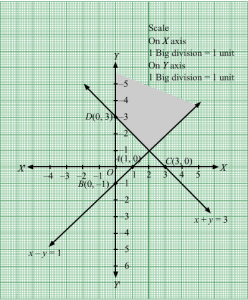
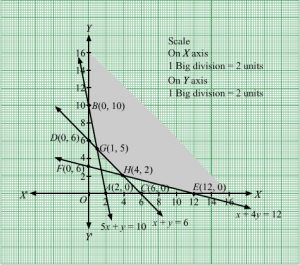
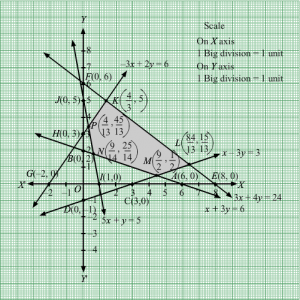
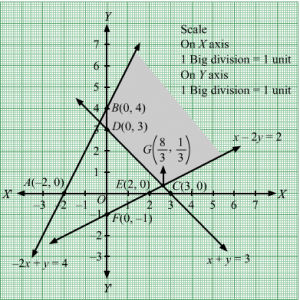
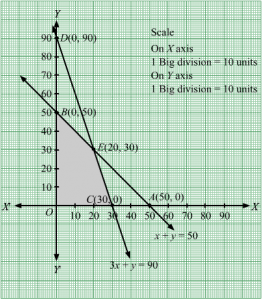
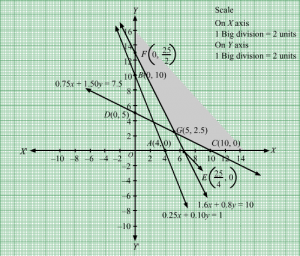
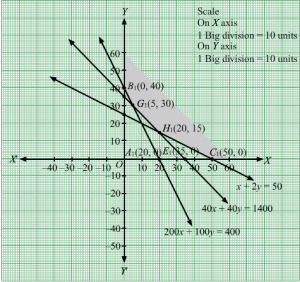
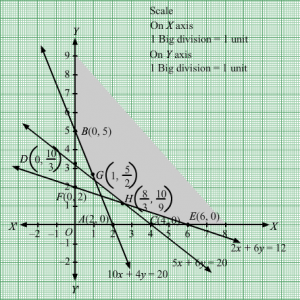
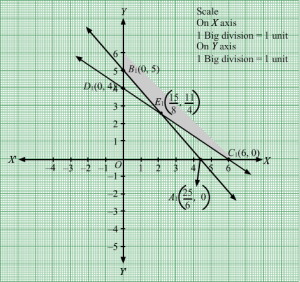
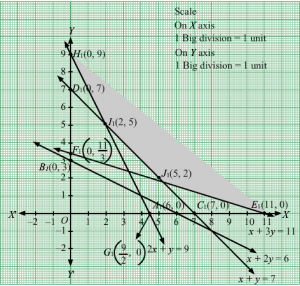
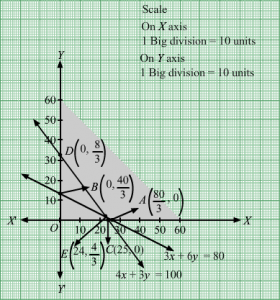
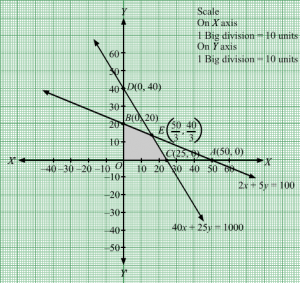
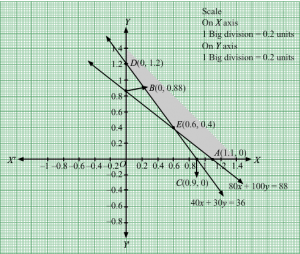
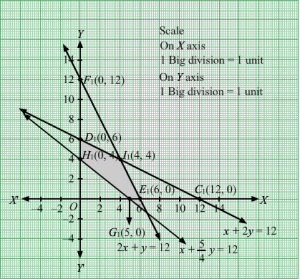
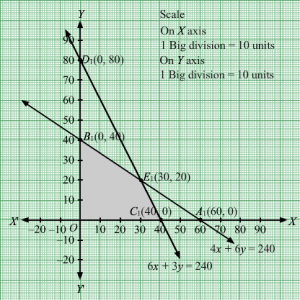
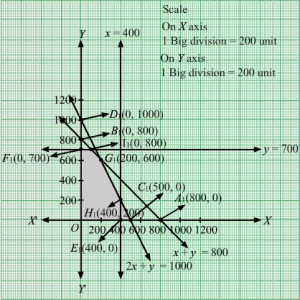
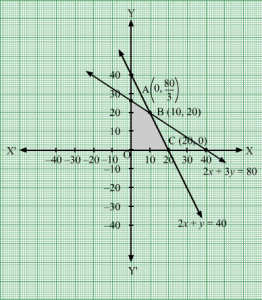
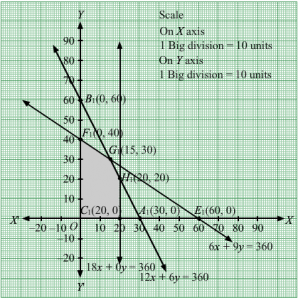
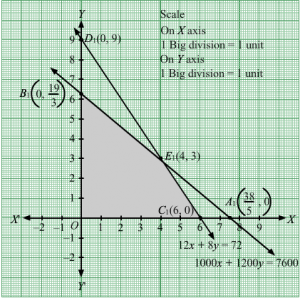
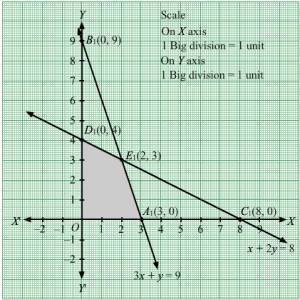
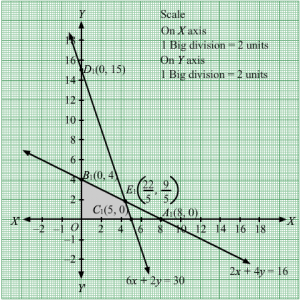
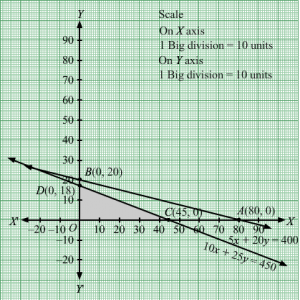
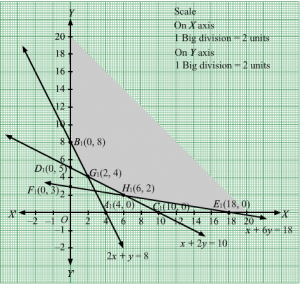
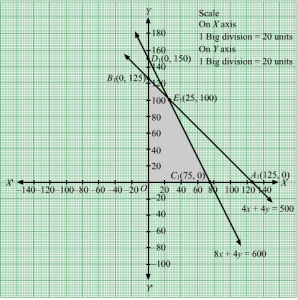
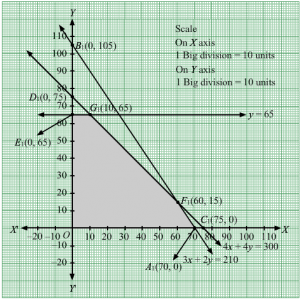
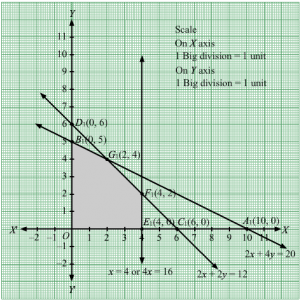

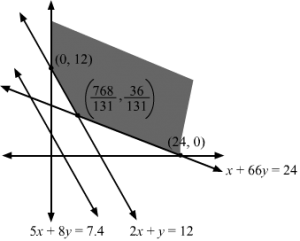
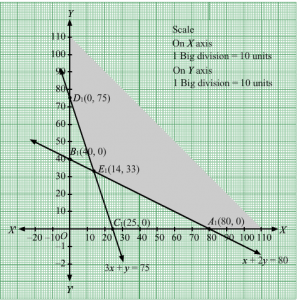
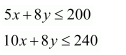
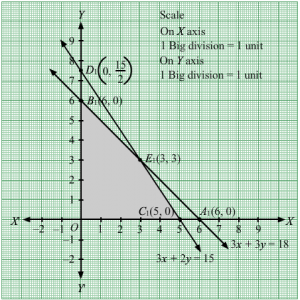
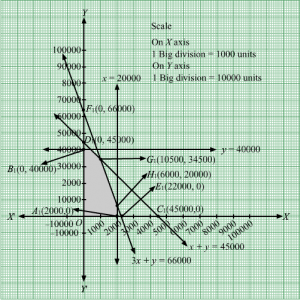
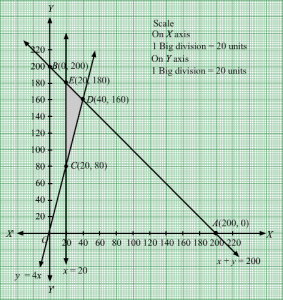
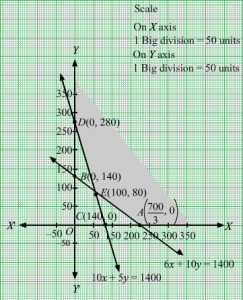
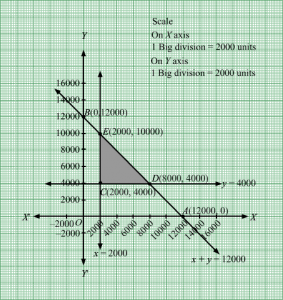
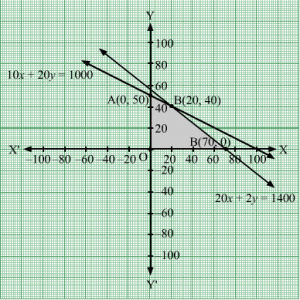
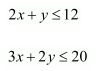
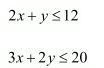
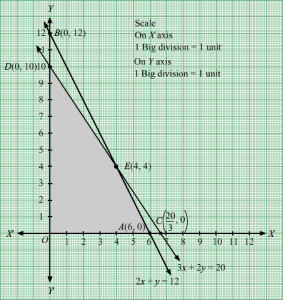

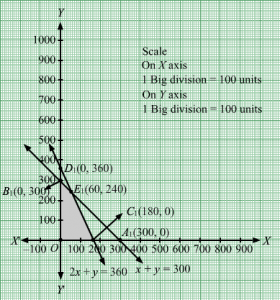
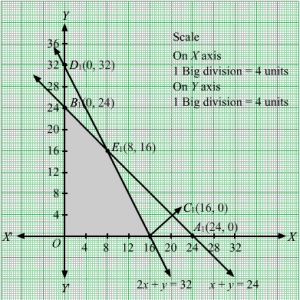
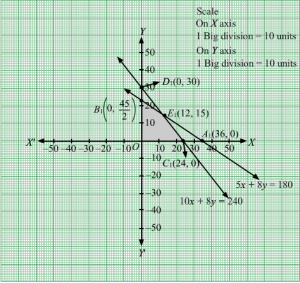
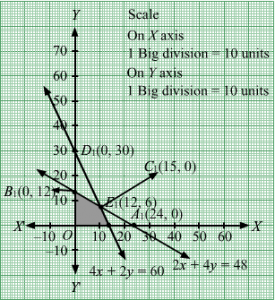
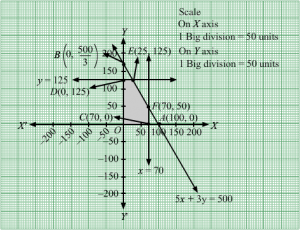
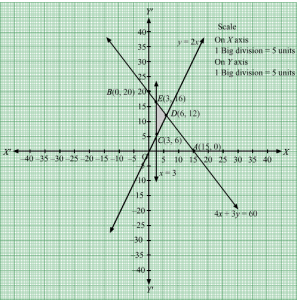
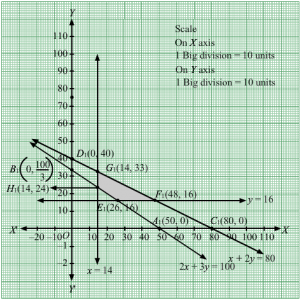
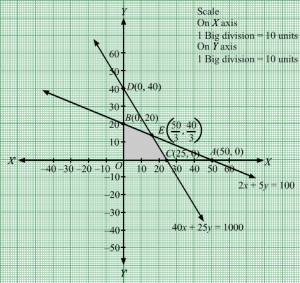
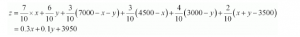
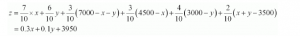
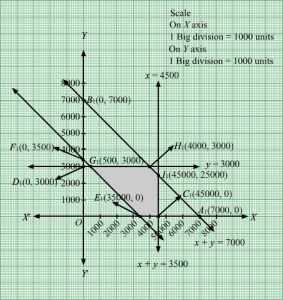
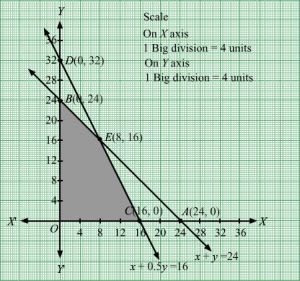
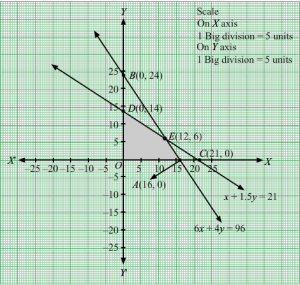
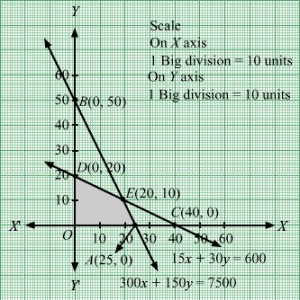
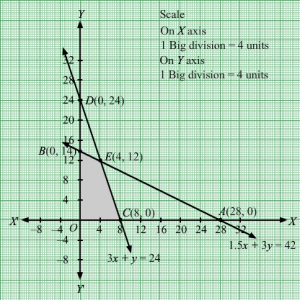
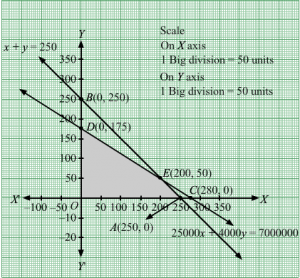
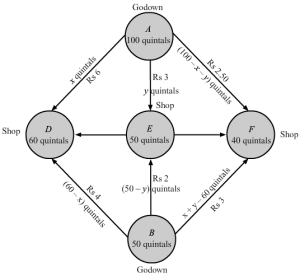
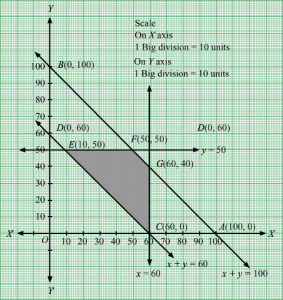
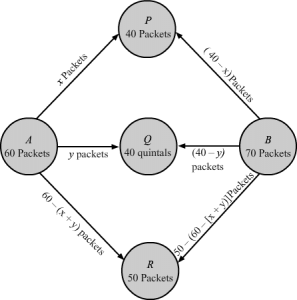

Leave a Reply