Page 27.22 Ex. 27.1
Q1.
Answer :
Let the direction cosines of the line be l, m, n.
Now,
l = cos900 = 0m = cos600 = 12n = cos300 = 32Therefore, the direction cosines of the line are 0, 12, 32.
Q2.
Answer :
Let the direction cosines of the line be l, m, n.Now, l = 222+-12+-22=23m = -122+-12+-22=-13n =-222+-12+-22=-23Therefore, the direction cosines of the line are 23 ,-13, -23.
Q3.
Answer :
The direction cosines of the line passing through two points P x1, y1, z1 and Q x2, y2, z2 are x2-x1PQ, y2-y1PQ,z2-z1PQ.Here,PQ=x2-x12 + y2-y12 + z2-z12P=-2, 4,-5 Q=1,2,3∴ PQ = 1–22 + 2-42 + 3 – -52 =77Thus, the direction cosines of the line joining two points are 1–277, 2-477, 3 – -577, i.e. 377, -277, 877.
Q4.
Answer :
The given points are A 2, 3, -4, B1, -2, 3 and C 3, 8, -11.We know that the direction ratios of the line joining the points, x1, y1, z1 and x2, y2, z2 are x2-x1, y2-y1, z2-z1.The direction ratios of the line joining A and B are 1-2, -2-3, 3+4, i.e.-1, -5, 7.The direction ratios of the line joining B and C are 3-1, 8+2, -11-3, i.e. 2, 10, -14.It is clear that the direction ratios of BC are -2 times that of AB, i.e. they are proportional.Therefore, AB is parallel to BC. Also, point B is common in both AB and BC. Therefore, points A, B and C are collinear.
Q5.
Answer :
The vertices of ∆ABC are A 3, 5, -4, B -1,1,2 and C -5, -5, -2.
The direction ratios of AB are -1-3, 1-5, 2–4, i.e. -4, -4, 6.Therefore, the direction cosines of AB are-4-42+-42+62, -4-42+-42+62, 6-42+-42+62=-4 217, -4217, 6217 = 217, 217, -317The direction ratios of BC are -5–1, -5-1, -2-2, i.e. -4, -6,-4.Therefore, the direction cosines of BC are-4-42+-62+-42, -6-42+-62+-42, -4-42+-62+-42=-4217, -6217, -4217 =217, 37, 217The direction ratios of CA are 3–5, 5–5, -4–2, i.e. 8, 10, -2.Therefore, the direction cosines of CA are882+102+-22, 1082+102+-22, -282+102+-22=8242, 10242, -2242 =442, 542, -142
Q6.
Answer :
Let a→ be a vector with direction ratios 1, -2, 1.⇒a → = i^ -2j^ + k^ . Let b→ be a vector with direction ratios 4, 3, 2.⇒b→=4i^ + 3j^ + 2k^.Let θ be the angle between the given vectors. Now,cos θ = a→.b→a→ b→ =i^ -2j^ + k^.4i^ + 3j^ + 2k^i^ -2j^ + k^4i^ + 3j^ + 2k^ = 4-6+21+4+1 16+9+4 = 06 29 = 0 ∴ θ =π2Thus, the angle between the given vectors measures π2.
Q7.
Answer :
Let a→ be a vector with direction ratios 2, 3, -6. ⇒ a→ = 2i^ +3j^ -6k^.Let b→ be a vector with direction ratios 3, -4, 5.⇒b→ = 3i^ -4j^ + 5k^Let θ be the angle between the given vectors. Now,cos θ = a→. b→a→ b→ =2i^ +3j^ -6k^.3i^ -4j^ + 5k^2i^ +3j^ -6k^3i^ -4j^ + 5k^ = 6-12-304+9+36 9+16+25 = -3649 50 =-36352Rationalising the result, we getcos θ = -18235 ∴ θ = cos-1-18235Thus, the angle between the given vectors measures cos-1-18235.
Q8.
Answer :
Given:l+m+n = 0 …12lm + 2ln -nm = 0 …2From 1, we getl=-m-nSubstituting l=-m-n in 2, we get2-m-nm +2-m-nn-mn = 0⇒-2m2-2mn -2mn-2n2-mn = 0⇒2m2+2n2+5mn = 0⇒m+2n 2m+n = 0 ⇒m =-2n, -n2If m=-2n, then from 1, we get l=n. If m= -n2 , then from 1, we get l=-n2.Thus, the direction ratios of the two lines are proportional to n, -2n, n and -n2, -n2, n, i.e. 1, -2, 1 and -12, -12, 1.Hence, their direction cosines are±16, ±-26, ±16 ±-16, ±-16, ±26
Q9.
Answer :
i) Given:l + m + n = 0 …(1) l2 + m2 – n2 = 0 …(2)From 1, we getm = -l-nSubstituting m=-l-n in 2, we getl2+ -l-n2-n2⇒l2 + l2 + n2 +2ln – n2 = 0⇒2l2 + 2ln = 0⇒2l l+n = 0⇒ l = 0 , l = -nIf l=0, then by substituting l=0 in 1, we get m =-n.If l=-n, then by substituting l=-n in 1, we get m=0.Thus, the direction ratios of the two lines are proportional to 0, -n, n and -n, 0, n or 0, -1, 1 and-1, 0, 1.Vectors parallel to these lines area→ = 0i^ -j^ +k^ b→ = -i^+0j^+k^ If θ is the angle between the lines, then θ is also the angle between a→ and b→.Now,cos θ = a→.b→a→ b→ =10+1+1 1+0+1 =12 ⇒θ=π3
ii) Given:2l – m + 2n = 0 …(1)mn + nl +lm= 0 …(2)From 1, we get m = 2l+2nSubstituting m = 2l+2n in 2, we get2l+2nn+nl+l2l+2n=0⇒2ln+2n2+nl+2l2+2ln= 0⇒2l2+5ln+2n2= 0 ⇒l+2n 2l+n= 0⇒l = -2n , -n2If l =-2n, then by substituting l= -2n in 1, we get m =-2n.If l = -n2, then by substituting l = -n2 in 1, we get m=n.Thus, the direction ratios of the two lines are proportional to-2n, -2n, n and -n2, n, n or -2, -2, 1 and -12, 1, 1.Vectors parallel these lines area→ = -2i^ -2j^ +k^b→ = -12i^+ j^+k^ If θ is the angle between the lines, then θ is also the angle between a→ and b.→Now,cos θ=a→.b→a→ b→ =1-2+14+4+1 14+1+1 =0 ⇒θ=π2
iii) Given:l + 2m + 3n = 0 …(1)3lm – 4ln +mn= 0 …(2)From 1, we get l=-2m-3nSubstituting l =-2m-3n in 2, we get3-2m-3nm-4-2m-3nn+mn=0⇒-6m2-9mn+8mn+12n2+mn=0⇒12n2-6m2= 0 ⇒m2=2n2⇒m = 2n, -2 nIf m=2n, then by substituting m=2n in 1, we get l =n-22 -3.If m= -2 n, then by substituting m=-2 n in 1, we get l=n22-3.Thus, the direction ratios of the two lines are proportional to n-22 -3,2n, n and n22-3, -2 n, n or -22 -3, 2 , 1 and -22 -3, -2, 1.Vectors parallel to these lines area→=-22 -3i^ +2 j^ +k^ b→=22 -3i^ -2 j^ +k^If θ is the angle between the lines, then θ is also the angle between a→ and b→.Now,cos θ = a→.b→a→ b→ =-22 -3i^ +2 j^ +k^.22 -3i^ -2 j^ +k^ 8+9+122+2+1 8+9-122+2+1 =-8-9-2+120+122 20-122 =020+122 20-122 =0⇒θ=π2
Q10.
Answer :
Let a→ be a vector parallel to the vector with direction ratios 2, 3, 6. ⇒a→=2i^+3j^+6k^. Let b→ be a vector parallel to the vector with direction ratios 1, 2, 2.⇒b→= i^ +2j^ +2k^Let θ be the angle between the the given vectors. Now,cos θ =a→.b→a→ b→ =2i^+3j^+6k^.i^ +2j^ +2k^2i^+3j^+6k^i^ +2j^ +2k^ = 2+6+12 4+9+36 1+4+4 = 2021 ⇒θ=cos-12021
Q11.
Answer :
Suppose the points are A 2,3,4, B -1.-2,1 and C 5,8,7.We know that the direction ratios of the line joining the points x1, y1, z1 and x2, y2, z2 are x2-x1, y2-y1, z2-z1.The direction ratios of AB are -1-2, -2-3, 1-4, i.e. -3, -5,-3.The direction ratios of BC are 5–1, 8–2, 7-1, i.e. 6, 10, 6.It can be seen that the direction ratios of BC are -2 times that of AB, i.e. they are proportional. Therefore, AB is parallel to BC. Since point B is common in both AB and BC, points A, B, and C are collinear.
Q12.
Answer :
We know that the direction ratios of the line passing through the points x1, y1, z1 and x2, y2, z2 are x2-x1, y2-y1, z2-z1.Let the first two points be A 4, 7, 8 and B 2, 3, 4.Thus, the direction ratios of AB are 2-4, 3-7, 4-8, i.e. -2, -4, -4.Similarly, let the other two points be C -1,-2, 1 and D1, 2, 5.Thus, the direction ratios of CD are 1–1, 2–2, 5-1, i.e. 2, 4, 4.It can be seen that the direction ratios of CD are-1 times that of AB, i.e. they are proportional.Therefore, AB and CD are parallel lines.
Q13.
Answer :
We know that two lines with direction ratios a1, b1, c1 and a2, b2, c2 are perpendicular if a1a2 + b1b2+c1c2=0.The direction ratios of the line passing through the points 1, -1, 2 and 3, 4, -2 are 3-1, 4–1, -2-2, i.e. 2, 5,-4.⇒a1=2, b1=5, c1 = -4Similarly, the direction ratios of the line passing through the points 0, 3, 2 and 3, 5, 6 are 3-0, 5-3, 6-2, i.e. 3, 2, 4.⇒a2=3, b2=2, c2=4∴ a1a2 + b1b2+c1c2 = 2×3 + 5×2 +-4×4 =6 +10 – 16 = 0
Thus, the line through the points (1, -1, 2) and (3, 4, -2) is perpendicular to the line through the points (0, 3, 2) and (3, 5, 6).
Q14.
Answer :
We know that two lines with direction ratios a1, b1, c1 and a2, b2, c2 are perpendicular if a1a2+b1b2+c1c2=0.The direction ratios of the line joining the origin 0, 0, 0 to the point 2, 1, 1 are 2-0, 1-0, 1-0 or 2, 1, 1.⇒a1=2, b1=1, c1=1Similarly, the direction ratios of the line joining the points 3, 5, -1 and 4, 3, -1 are 4-3, 3-5, -1–1 or 1, -2, 0.⇒a2=1, b2=-2, c2=0∴ a1a2+b1b2+c1c2= 2 -2 + 0=0
Therefore, the line joining the origin to the point (2, 1, 1) is perpendicular to the line determined by the points (3, 5, -1) and (4, 3, -1).
Q15.
Answer :
Let θ be the angle between the given lines.We have a1=a, b1=b, c1=c a2=b-c, b2=c-a, c2=a-bNow,cos θ = a1a2+b1b2+c1c2a12+b12+c12a22+b22+c22 =ab-c+bc-a+ca-ba2+b2+c2b-c2+c-aa-b=ab-ac+bc-ab+ac-bca2+b2+c2b-c2+c-aa-b=0⇒θ=π2Thus, the angle between the given lines measures 90°.
Q16.
Answer :
The given points are A 1, 2, 3, B4, 5, 7, C-4, 3, -6 and D 2, 9, 2.We know that the direction ratios of the line joining the points x1, y1, z1 and x2, y2, z2 are x2-x1, y2-y1, z2-z1.The direction ratios of AB are 4-1, 5-2, 7-3, i.e. 3, 3, 4.The direction ratios of CD are 2–4, 9-3, 2–6, i.e. 6, 6, 8.Let θ be the angle between AB and CD.We havea1=3, b1=3, c1=4 a2=6, b2=6, c2=8∴ cos θ =a1a2+b1b2+c1c2a12+b12+c12a22+b22+c22=18+18+329+9+1636+36+64=6868=1⇒ θ =0°Thus, the angle between AB and CD measures 0°.
Page 27.22 (Very Short Answers)
Q1.
Answer :
The direction cosines of a directed line segment are the cosines of the direction angles of the line segment.Let two points A x1, y1, z1 and B x2, y2, z2 define the directed line segment AB. The direction cosines of AB are given bycos α =x2-x1dcos β =y2-y1dcosγ = z2-z1dHere, d is the distance between A and B.
Q2.
Answer :
The x-axis makes angles 0°, 90° and 90°with x, y and z axes, respectively.Therefore, the direction cosines of x-axis are cos 0°, cos 90°, cos 90°, i.e. 1, 0, 0.
Q3.
Answer :
The y-axis makes angles 90°, 0°and 90° with x, y and z axes, respectively .Therefore, the direction cosines of y-axis are cos 90°, cos 0°, cos 90°, i.e. 0, 1, 0.
Q4.
Answer :
The z-axis makes angles 90°, 90° and 0° with x, y and z axes, respectively.Therefore, the direction cosines of z-axis are cos 90°, cos 90°, cos 0°, i.e. 0, 0, 1.
Q5.
Answer :
The distance of a general point P x, y, z from XY-plane is z.Thus, distance of 7, -2, 3 from XY-plane is 3.Similarly, the distance of P x, y, z from YZ-plane is x.Thus, distance of 7, -2, 3 from YZ- plane is 7.The distance of P x, y, z from XZ-plane is y.Thus, distance of 7, -2, 3 from XZ-plane is 2.
Q6.
Answer :
The distance of a general point x, y, z from x-axis is y2+z2.∴ Distance of the point 3, -5, 12 from x-axis=-52+122 = 169 = 13 units
Q7.
Answer :
Let the YZ-plane divide the line segment joining points P-2, 5, 9 and Q 3, -2, 4 in the ratio k:1.Using the section formula, the coordinates of the point of intersection are given byk3-2k+1, k-2+5k+1, k4+9k+1On the YZ-plane, the X-coordinate of any point is zero.∴ k3-2k+1=0⇒3k-2=0⇒k=23Thus, the YZ-plane divides the line segment formed by joining the given points in the ratio 2:3 internally.
Q8.
Answer :
It is given that a line makes an angle of 60° with both x-axis and y-axis.Suppose the line makes an angle of α with the z-axis.⇒l= cos 60°= 12m= cos 60°=12 n= cos αWe know l2+ m2+n2=1⇒122 +122 + cos α2 =1⇒ 14 + 14 + cos 2 α =1⇒cos α=12⇒α=45°Thus, the line makes an angle of 45° with the z-axis.
Q9.
Answer :
It is given that the the line makes angles α, β, γ with the coordinate axis.∴ l=cos α, m=cos β and n=cos γ⇒l2+m2+n2=1⇒ cos2 α+cos2 β+cos2 γ=1 …1Now,cos 2α + cos 2β + cos 2γ = 2cos2 α-1+2cos2 β-1+2cos2 γ-1 =2cos2 α+cos2 β+cos2 γ -3 =21-3 From 1 =-1
Q10.
Answer :
Suppose the line segment joining the points a, b, c and -a, -c, -b is divided by the XY-plane at a point R in the ratio λ:1. Coordinates of R areλ-a+1aλ+1, λ-c+1bλ+1, λ-b+1cλ+1Since R lies on XY-plane, Z-coordinate of R must be zero.⇒λ-b+1cλ+1 = 0= cb Thus, the required ratio is cb:1 or c:b.Hence, the XY-plane divides the line in the ratio c:b.
Q11.
Answer :
We know that if a line has direction ratio a, b, c, then the cosine of its angle with the z-axis is given bycos γ = ca2+b2+c2Suppose the inclination of the line with direction ratio 0, 1, -1 with z-axis is γ.Now,cos λ = -10+1+1 =-12 ⇒λ=3π4Hence, the inclination of the line with z-axis is 3π4.
Q12.
Answer :
The direction ratios of the first line are 1, -2, 1 and the direction ratios of the second line are 4, 3, 2.Let θ be the angle between these two lines.Now,cos θ=14+-23+1212+-22+12 42+32+22 =4-6+21+4+116+9+4 =0629 =0 ⇒θ=π2Hence, the required angle is π2.
Q13.
Answer :
The distance of the point P x, y, z from the XOY plane is z.
Q14.
Answer :
The projection of the point P (x, y, z) on XOZ-plane is (x, 0, z) as Y-coordinates of any point on XOZ-plane are equal to zero.
Page 27.24 (Very Short Answers)
Q15.
Answer :
The coordinates of the projection of the point P ( 2, -3, 5) on the y-axis are ( 0, -3, 0) as both X and Z coordinates of each point on the y-axis are equal to zero.
Q16.
Answer :
A general point (x, y, z) is at a distance of y2+z2 from the x-axis.∴ Distace of the point (2, 3, 4) from x-axis = 32+42 = 25 = 5 units
Q17.
Answer :
If a line has direction ratios proportional to 2, -1, and -2, then its direction cosines are 222+-1+-22, -122+-1+-22, -222+-1+-22 = 23, -13, -23Thus, the direction cosines are 23, -13, -23.
Q18.
Answer :
A line parallel to z-axis, makes an angle of 90°, 90° and 0° with the x, y and z axes, respectively.Thus, the direction cosines are given byl = cos 90° =0 m = cos 90° = 0 n = cos 0 =1Therefore, direction cosines of a line parallel to the z-axis are 0, 0, 1.
Q19.
Answer :
Since a unit vector makes an angle of π3 with i^, π4 with j^ and an acute angle θ with k^, l = cos π3 or 12, m =cos π4or12 and n= cos θ.We knowl2+m2+n2=1⇒ 122 + 122 + cos2 θ = 1⇒14 + 12 + cos2 θ = 1 ⇒ cos2 θ = 14⇒ cos θ = 12 ⇒ θ = π3Thus, the vector a→ makes an angle of π3 with k^
Page 27.24 (Multiple Choice Questions)
Q1.
Answer :
(c) z = 0
The Z-coordinate of every point on the XY-plane is zero.
Q2.
Answer :
c) y=0, z = 0, x ≠ 0 Both Y and Z coordinates on each point of the x-axis are equal to zero. The X-coordinate on the origin is also equal to zero.Therefore, the Y and Z coordinates on each point of the x-axis, except the origin, are equal to zero, while the X-coordinate is non-zero.
Q3.
Answer :
d) all of theseThe given points 5, 7, 9 and 2, 3, 7 are two diagonally opposite vertices of the parallelopiped as all of their coordinates are different.∴ Edges of the parallelopiped = 5-2, 7-3, 9-7 =3, 4, 2
Q4.
Answer :
a) 7
The given points 2, 3, 5 and 5, 9, 7 are two diagonally opposite vertices of the parallelopiped as all of their coordinates are different. ∴ Edges of the parallelopiped=2-5, 3-9 and 5-7 =3, 6 and 2Now,Length of the diagonal of the parallelopiped=32+62+22 =9+36+4 =49 = 7Hence, length of the diagonal of the parallelopiped formed by the planes parallel to coordinate planes and drawn through points 2, 3, 5 and 5, 9, 7 is 7 units.
Q5.
Answer :
b) externally in the ratio 2:3Let the XY-plane divide the line segment joining points P-1, 3, 4 and Q2, -5, 6 in the ratio k:1.Using the section formula, the coordinates of the point of intersection are given byk2-1k+1, k-5+3k+1, k6+4k+1On the XY-plane, the Z-coordinate of any point is zero.⇒ k6+4k+1=0⇒6k+4=0⇒k=-23Thus, the XY-plane divides the line segment joining the given points in the ratio 2:3 externally.
Q6.
Answer :
c) -1Suppose the point P divides the line joining the point Q 2, 2, 1 and R 5, 1, -2 in the ratio k:1.Using the section formula, the coordinates of the point of intersection are given byk5+2k+1, k1+2k+1, k-2+1k+1It is given that the X-coordinate of P is 4.⇒k5+2k+1=4⇒5k+2=4k+1⇒ k=2Now,Z-coordinate of P =k-2+1k+1 = 2-2+12+1 Substituting k=2 =-1
Q7.
Answer :
a) b2+c2The projection of the point P a, b, c on the x-axis is a, 0, 0 as both Y and Z coordinates on any point on the x-axis are equal to zero. ∴ Distance of P a, b, c from x-axis = Distance of P a, b, c from a, 0, 0 = a-a2+b-02+c-02 =b2+c2
Q8.
Answer :
b) 3:1 externallySuppose the XY-plane divides the line segment joining the points P 1, 2, 3 and Q 4, 2, 1 in the ratio k:1.Using the section formula, the coordinates of the point of intersection are given byk4+1k+1, k2+2k+1,k1+3k+1The Z-coordinate of any point on the XY-plane is zero.⇒k1+3k+1=0⇒k+3 = 0⇒k=-3=-31Thus, the XY-plane divides the line segment joining the given points in the ratio 3:1 externally.
Q9.
Answer :
b) 3:2 externallySuppose the point R divides PQ in the ratio λ:1.Coordinates of R are 5λ+3λ+1, 4λ+2λ+1, -6λ-4λ+1.But the coordinates of R are 9, 8, -10.∴ 5λ+3λ+1=9, 4λ+2λ+1=8 and -6λ-4λ+1=-10From each of these equations, we getλ=-32∴ R divides PQ in the ratio 3:2 externally.
Q10.
Answer :
Since the bisector of ∠ABC cannot meet BC, the solution of this question is not possible.
Disclaimer:This question is wrong, so the solution has not been provide.
Page 27.25 (Multiple Choice Questions)
Q11.
Answer :
a -1, 2,-2Let the coordinates of P be x, y, z. Then,Direction ratios of OP= Coordinates of P- Coordinates of O-1, 2, 2 = x-0, y-0, z-0Thus, coordinates of P are -1, 2,-2.
Q12.
Answer :
(d) cos-113
Let a be the length of an edge of the cube and let one corner be at the origin as shown in the figure. Clearly, OP, AR, BS, and CQ are the diagonals of the cube.Consider the diagonals OP and AR.Direction ratios of OP and AR are proportional to a-0, a-0, a-0 and 0-a, a-0, a-0, i.e. a, a, a and -a, a, a, respectively.Let θ be the angle between OP and AR. Then,cos θ =a×-a+a×a+a×aa2+a2+a2-a2+a2+a2⇒cos θ =-a2+a2+a23a23a2⇒ cos θ =13 ⇒θ = cos-1 13 Similarly, the angles between other pairs of the diagonals are equal to cos-1 13 as the angle between any two diagonals of a cube is cos-1 13.
Q13.
Answer :
c) 43
Let a be the length of an edge of the cube and let one corner be at the origin as shown in the figure. Clearly, OP, AR, BS and CQ are the diagonals of the cube. The direction ratios of OP, AR, BS and CQ area-0, a-0, a-0, i.e. a, a, a0-a, a-0, a-0, i.e. -a, a, aa-0, 0-a, a-0, i.e. a, -a, aa-0, a-0, 0-a, i.e. a, a,-a Let the direction ratios of a line be proportional to l, m and n. Suppose this line makes angles α, β, γ and δ with OP, AR, BS and CQ, respectively.Now, α is the angle between OP and the line whose direction ratios are proportional to l, m and n. cos α = a.l+a.m+a.na2+a2+a2l2+m2+n2⇒cos α = l + m + n3l2+m2+n2Since β is the angle between AR and the line with direction ratios proportional to l, m and n, we get cos β = -a.l+a.m+a.na2+a2+a2l2+m2+n2⇒ cos β=-l+m+n3l2+m2+n2Similarly, cos γ = a.l-a.m+a.na2+a2+a2l2+m2+n2⇒ cos γ=l – m + n3l2+m2+n2 cos δ = a.l+a.m-a.na2+a2+a2l2+m2+n2⇒ cos δ=l+m – n3l2+m2+n2cos2α + cos2β + cos2γ+cos2δ =l+m+n23l2+m2+n2+-l+m+n23l2+m2+n2+I-m+n23l2+m2+n2+l+m – n23l2+m2+n2 =13l2+m2+n2l+m+n2+-l+m+n2+I-m+n2+l+m -n2 =13l2+m2+n24l2+m2+n2 =43
Page 28.9 Ex. 28.1
Q1.
Answer :
We know that the vector equation of a line passing through a point with position vector a→ and parallel to vector b→ is r→ = a→ + λ b→.
Here,
a→ = 5i^+2j^-4k^b→ =3i^+2j^-8k^
Vector equation of the required line is given by
r→ = 5i^+2j^-4k^ + λ 3i^+2j^-8k^ …1 Here, λ is a parameter.
Reducing (1) to cartesian form, we get
xi^+yj^+zk^ = 5i^+2j^-4k^ + λ 3i^+2j^-8k^ [Putting r→ = xi^+yj^+zk^ in (1)]⇒xi^+yj^+zk^ = 5+3λ i^+2+2 λ j^+-4-8 λ k^Comparing the coefficients of i^, j^ and k^, we getx=5+3λ, y=2+2 λ, z=-4-8 λ⇒x-53=λ, y-22=λ, z+4-8=λ⇒x-53=y-22=z+4-8=λHence, the cartesian form of (1) isx-53=y-22=z+4-8
Q2.
Answer :
We know that the vector equation of a line passing through the points with position vectors a→ and b→ is r→ = a→ + λ b→-a→, where λ is a scalar.
Here,
a→ =-1i^+0j^+2k^b→= 3i^+4j^+6k^
Vector equation of the required line is
r→=-1i^+0j^+2k^ + λ 3i^+4j^+6k^–1i^+0j^+2k^⇒r→=-1i^+0j^+2k^ + λ 4i^+4j^+4k^Here, λ is a parameter.
Q3.
Answer :
We know that the vector equation of a line passing through a point with position vector a→ and parallel to the vector b→ is r→ = a→ + λ b→.
Here,
a→ = 5i^-2j^+4k^b→ = 2i^-j^+3k^
So, the vector equation of the required line is
r→ = 5i^-2j^+4k^ + λ 2i^-j^+3k^ …(1) Here, λ is a parameter.
Reducing (1) to cartesian form, we get
xi^+yj^+zk^= 5i^-2j^+4k^ +λ 2i^-j^+3k^ [Putting r→=xi^+yj^+zk^ in (1)]⇒xi^+yj^+zk^ = 5+2λ i^+-2-λ j^+4+3λ k^Comparing the coefficients of i^, j^ and k^, we getx=5+2λ, y=-2-λ, z=4+3λ⇒x-52=λ, y+2-1=λ, z-43=λ⇒x-52=y+2-1=z-43=λHence, the cartesian form of (1) isx-52=y+2-1=z-43
Q4.
Answer :
We know that the vector equation of a line passing through a point with position vector a→ and parallel to the vector b→ is r→ = a→ + λ b→.
Here,
a→ = 2i^-3j^+4k^ b→ = 3i^+4j^-5k^.
So, the vector equation of the required line is
r→ = 2i^-3j^+4k^ + λ 3i^+4j^-5k^ …(1)Here, λ is a parameter.
Reducing (1) to cartesian form, we get
xi^+yj^+zk^ = 2i^-3j^+4k^ + λ 3i^+4j^-5k^ [Putting r→ = xi^+yj^+zk^ in (1)]⇒xi^+yj^+zk^ = 2+3λ i^+-3+4λ j^+4-5λ k^Comparing the coefficients of i^, j^ and k^, we getx=2+3λ, y=-3+4λ, z=4-5λ⇒x-23=λ, y+34=λ, z-4-5=λ⇒x-23=y+34=z-4-5=λHence, the cartesian form of (1) isx-23=y+34=z-4-5
Q5.
Answer :
We know that the position vector of the mid-point of a→ and b→ is a→+b→2.
Let the position vector of point D be xi^+yj^+zk^.
Position vector of mid-point of A and C = Position vector of mid-point of B and D
∴ 4i^+5j^-10k^+-i^+2j^+k^2=2i^-3j^+4k^+xi^+yj^+zk^2⇒32i^+72j^-92k^=x+22i^+-3+y2j^+4+z2k^Comparing the coefficient of i^, j^ and k^, we getx+22=32⇒x=1-3+y2=72⇒y=10 4+z2=-92⇒ z=-13Position vector of point D=i^+10j^-13k^
The vector equation of line BD passing through the points with position vectors a→(B) and b→(D) is r→ = a→ + λ b→-a→.
Here,
a→ = 2i^-3j^+4k^ b→ =i^+10j^-13k^
Vector equation of the required line is
r→ = 2i^-3j^+4k^+λi^+10j^-13k^-2i^-3j^+4k^⇒r→ = 2i^-3j^+4k^ + λ -i^+13j^-17k^ …(1) Here, λ is a parameter.
Reducing (1) to cartesian form, we get
xi^+yj^+zk^ = 2i^-3j^+4k^ + λ -i^+13j^-17k^ [Puttingr →= xi^+yj^+zk^ in (1)]⇒xi^+yj^+zk^ = 2-λ i^+-3+13λ j^+4-17λ k^Comparing the coefficients of i^, j^ and k^, we getx=2-λ, y=-3+13λ, z=4-17λ⇒x-2-1=λ, y+313=λ, z-4-17=λ⇒x-2-1=y+313=z-4-17=λ⇒x-21=y+3-13=z-417=-λHence, the cartesian form of (1) isx-21=y+3-13=z-417
Q6.
Answer :
We know that the vector equation of a line passing through the points with position vectors a→ and b→ is r→ = a→ + λ b→-a→, where λ is a scalar.
Here,
a→ = i^+2j^-k^ b→ =2i^+j^+k^
Vector equation of the required line is
r→ = i^+2j^-k^+λ2i^+j^+k^-i^+2j^-k^⇒r→ = i^+2j^-k^ + λi^-j^+2k^ …(1) Here, λ is a parameter.
Reducing (1) to cartesian form, we get
xi^+yj^+zk^ = i^+2j^-k^ + λi^-j^+2k^ [Putting r→=xi^+yj^+zk^ in (1)]⇒xi^+yj^+zk^ = 1+λ i^+2-λ j^+-1+2λ k^Comparing the coefficients of i^, j^ and k^, we getx=1+λ, y=2-λ, z=-1+2λ⇒x-1=λ, y-2-1=λ, z+12=λ⇒x-11=y-2-1=z+12=λHence, the cartesian form of (1) isx-11=y-2-1=z+12
Q7.
Answer :
We know that the vector equation of a line passing through a point with position vector a→ and parallel to the vector b→ is r→ = a→ + λ b→.
Here,
a→ =i^+2j^+3k^ b→ =i^-2j^+3k^
Vector equation of the required line is
r→ = i^+2j^+3k^ + λ i^-2j^+3k^ … (1)Here, λ is a parameter.
Reducing (1) to cartesian form, we get
xi^+yj^+zk^ = i^+2j^+3k^ + λ i^-2j^+3k^ [Putting r→=xi^+yj^+zk^ in (1)]⇒xi^+yj^+zk^ = 1+λ i^+2-2λ j^+3+3λ k^Comparing the coefficients of i^, j^ and k^, we getx=1+λ, y=2-2λ, z=3+3λ⇒x-1=λ, y-2-2=λ, z-33=λ⇒x-11=y-2-2=z-33=λHence, the cartesian form of (1) isx-11=y-2-2=z-33
Page 28.10 Ex. 28.1
Q8.
Answer :
We know that the vector equation of a line passing through a point with position vector a→ and parallel to the vector b→ is r→ = a→ + λ b→.
Here,
a→ =2i^-j^+k^ b→ =2i^+7j^-3k^
Vector equation of the required line is
r→ = 2i^-j^+k^ + λ 2i^+7j^-3k^Here, λ is a parameter.
Q9.
Answer :
The cartesian equation of the given line is x-53=y+47=z-62.
It can be re-written as
x-53=y–47=z-62
Thus, the given line passes through the point having position vector a→=5i^-4j^+6k^ and is parallel to the vector b→=3i^+7j^+2k^.
We know that the vector equation of a line passing through a point with position vector a→ and parallel to the vector b→ is r→ = a→ + λ b→.
Vector equation of the required line is
r→ = 5i^-4j^+6k^ + λ 3i^+7j^+2k^Here, λ is a parameter.
Q10.
Answer :
We know that the cartesian equation of a line passing through a point with position vector a→ and parallel to the vector m→ is x-x1a=y-y2b=z-z3c.
Here,
a→=x1i^+y1j^+z1k^ m→=ai^+bj^+ck^
Here, a→ =i^-j^+2k^ and b→ =i^+2j^-2k^
Cartesian equation of the required line is
x-11=y–12=z-2-2⇒x-11=y+12=z-2-2
We know that the cartesian equation of a line passing through a point with position vector a→ and parallel to the vector m→ is r→=a→+λm→.
Here, the line is passing through the point 1, 1, -2 and its direction ratios are proportional to 1, 2, -2.
Vector equation of the required line is
r→=i^-j^+2k^+λi^+2j^-2k^
Q11.
Answer :
The cartesian equation of the given line is
4-x2=y6=1-z3
It can be re-written as
x-4-2=y-06=z-1-3
This shows that the given line passes through the point 4, 0 ,1 and its direction ratios are proportional to -2, 6, -3.
So, its direction cosines are
-2-22+62+-32, 6-22+62+-32, -3-22+62+-32=-27, 67, -37
Thus, the given line passes through the point having position vector a→=4i^+k^ and is parallel to the vector b→=-2i^+6j^-3k^.
We know that the vector equation of a line passing through a point with position vector a→ and parallel to the vector b→ is r→ = a→ + λ b→.
Here,
a→ =4i^+k^ b→ = -2i^+6j^-3k^
Vector equation of the required line is
r→ = 4i^+0j^+k^ + λ -2i^+6j^-3k^ Here, λ is a parameter.
Q12.
Answer :
The cartesian equation of the given line is
x=ay+b, z=cy+d
It can be re-written as
x-ba=y-01=z-dc
Thus, the given line passes through the point b, 0, d and its direction ratios are proportional to a, 1, c. It is also parallel to the vector b→=ai^+j^+ck^.
We know that the vector equation of a line passing through a point with position vector a→ and parallel to the vector b→ is r→ = a→ + λ b→.
Vector equation of the required line is
r→ = bi^+0j^+dk^ + λ ai^+j^+ck^Here, λ is a parameter.
Q13.
Answer :
We know that the vector equation of a line passing through a point with position vector a→ and parallel to the vector b→ is r→ = a→ + λ b→.
Here,
a→=i^-2j^-3k^ b→= 2i^+j^+2k^-i^-j^+4k^=i^+2j^-2k^
Vector equation of the required line is
r→ = i^-2j^-3k^ + λ i^+2j^-2k^ …(1)Here, λ is a parameter.
Reducing (1) to cartesian form, we get
xi^+yj^+zk^ = i^-2j^-3k^ + λ i^+2j^-2k^ [Putting r→= xi^+yj^+zk^ in (1)]⇒xi^+yj^+zk^ = 1+λ i^+-2+2 λ j^+-3-2λ k^Comparing the coefficients of i^, j^ and k^, we getx=1+λ, y=-2+2 λ, z=-3-2λ⇒x-11=λ, y+22=λ, z+3-2=λ⇒x-11=y+22=z+3-2=λHence, the cartesian form of (1) isx-11=y+22=z+3-2
Q14.
Answer :
The coordinates of any point on the line x+23=y+12=z-32 are given by
x+23=y+12=z-32=λ⇒x=3λ-2, y=2λ-1, z=2λ+3 …(1)
Let the coordinates of the desired point be 3λ-2, 2λ-1, 2λ+3 .
The distance between this point and (1, 3, 3) is 5 units.
∴ 3λ-2-12+2λ-1-32+2λ+3-32=5⇒3λ-32+2λ-42+2λ2=25⇒17λ2-34λ=0⇒λλ-2=0⇒λ=0 or 2
Substituting the values of λ in (1), we get the coordinates of the desired point as (-2, -1, 3) and (4, 3, 7).
Q15.
Answer :
Let the given points be P, Q and R and let their position vectors be a→, b→ and c→, respectively.
a→=-2i^+3j^b→=i^+2j^+3k^ c→=7i^+9k^
Vector equation of line passing through P and Q is
r→=a→+λb→-a→⇒r→=-2i^+3j^+λi^+2j^+3k^–2i^+3j^⇒r→=-2i^+3j^+λ3i^-j^+3k^ …(1)
If points P, Q and R are collinear, then point R must satisfy (1).
Replacing r→ by c→=7i^+9k^ in (1), we get
7i^+9k^=-2i^+3j^+λ3i^-j^+3k^
Comparing the coefficients of i^, j^ and k^, we get
7=-2+3λ, 0=3-λ, 9=3λ
∴ λ=3
These three equations are consistent, i.e. they give the same value of λ.
Hence, the given three points are collinear.
Q16.
Answer :
We have
-x-21=y+37=2z-63
It can be re-written as
x+2-1=y+37=z-332=x+2-2=y+314=z-33
This shows that the given line passes through the point -2, -3, 3 and its direction ratios are proportional to -2, 14, 3.
Thus, the parallel vector is b→=-2i^+14j^+3k^.
We know that the vector equation of a line passing through a point with position vector a→ and parallel to the vector b→ is r→ = a→ + λ b→.
Here,
a→ = i^+2j^+3k^ b→=-2i^+14j^+3k^.
Vector equation of the required line is
r→ = i^+2j^+3k^ + λ -2i^+14j^+3k^ …(1)Here, λ is a parameter.
Reducing (1) to cartesian form, we get
xi^+yj^+zk^ = i^+2j^+3k^ + λ -2i^+14j^+3k^ [Putting r→=xi^+yj^+zk^ in (1)]⇒xi^+yj^+zk^ = 1-2λ i^+2+14 λ j^+3+3λ k^Comparing the coefficients of i^, j^ and k^, we getx=1-2λ, y=2+14 λ, z=3+3λ⇒x-1-2=λ, y-214=λ, z-33=λ⇒x-1-2=y-214=z-33=λHence, the cartesian form of (1) is x-1-2=y-214=z-33
Q17.
Answer :
The cartesian equation of the given line is
3x + 1 = 6y − 2 = 1 − z
It can be re-written as
x+1313=y-1316=z-1-1=x–132=y-131=z-1-6
Thus, the given line passes through the point -13,13,1 and its direction ratios are proportional to 2, 1, -6. It is parallel to the vector b→=2i^+j^-6k^.
We know that the vector equation of a line passing through a point with position vector a→ and parallel to the vector b→ is r→ = a→ + λ b→.
Vector equation of the required line is
r→ = -13i^+13j^+k^ + λ 2i^+j^-6k^Here, λ is a parameter.
Page 28.15 Ex. 28.2
Q1.
Answer :
The direction cosines of the three lines are
l1=1213, m1=-313, n1=-413l2=413, m2=1213, n1=313l3=313, m3=-413, n3=1213
∴ l1l2+m1m2+n1n2=48-36-12169=0Also,l2l3+m2m3+n2n3=12-48+36169=0l1l3+m1m3+n1n3=36+12-48169=0
Hence, the given lines are perpendicular to each other.
Q2.
Answer :
Suppose vector a→ is passing through the points (1, -1, 2) and (3, 4,-2) and b→ is passing through the points (0, 3, 2) and (3, 5, 6).
Then,
a→=2i^+5j^-4k⏜ b→=3i^+2j^+4k⏜
Now,
a→.b→=2i^+5j^-4k⏜.3i^+2j^+4k⏜=0
Hence, the given lines are perpendicular to each other.
Q3.
Answer :
Equations of lines passing through the points x1, y1, z1 and x2, y2, z2 are given by
x-x1x2-x1=y-y1y2-y1=z-z1z2-z1
So, the equation of a line passing through (4, 7, 8) and (2, 3, 4) is
x-42-4=y-73-7=z-84-8⇒x-4-2=y-7-4=z-8-4
Also, the equation of the line passing through the points (-1, -2, 1) and (1, 2, 5) is
x+11+1=y+22+2=z-15-1⇒x+12=y+24=z-14
We know that two lines are parallel if
a1a2=b1b2=c1c2 Cartesian equations of the two lines are given by x-x1a1=y-y1b1=z-z1c1 and x-x2a2=y-y2b2=z-z2c2
We observe
-22=-44=-44=-1
Hence, the given lines are parallel to each other.
Q4.
Answer :
We know that the cartesian equation of a line passing through a point with position vector a→ and parallel to the vector b→ is x-x1a=y-y2b=z-z3c.
Here,
a→ =-2i^+4j-5k^b→ =3i^+5j^-6k^
The cartesian equation of the required line is
x–23=y-45=z–56=x+23=y-45=z+56
Q5.
Answer :
We have
x-57=y+2-5=z1 and x1=y2=z3
These equations can be re-written as
x-57=y–2-5=z-01 …(1) x-01=y-02=z-03 …(2)
∴ m1 →=Vector parallel to line (1) =7i^-5j^+k^ m2 →=Vector parallel to line (2) =i^+2j^+3k^
Now,
m1→.m2→=7i^-5j^+k^.i^+2j^+3k^ =7-10+3 =0
Hence, the given two lines are perpendicular to each other.
Page 28.16 Ex. 28.2
Q6.
Answer :
The direction ratios of the line joining the origin to the point (2, 1, 1) are 2, 1, 1.
Let b1→=2i^+j^+k^
The direction ratios of the line joining the points (3, 5, -1) and (4, 3, -1) are 1, -2, 0.
Let b2→=i^-2j^+0k^
Now,
b1→.b2→=2i^+j^+k^.i^-2j^+0k^ =2-2+0 =0∴ b1→⊥b2→
Hence, the two lines joining the given points are perpendicular to each other.
Q7.
Answer :
The direction ratios of the line parallel to x-axis are proportional to 1, 0, 0.
Equation of the line passing through the origin and parallel to x-axis is
x-01=y-00=z-00=x1=y0=z0
Q8.
Answer :
(i) r→=4i^-j^+λi^+2j^-2k^ and r→=i^-j^+2k^-μ2i^+4j^-4k^
Let b1→ and b2→ be vectors parallel to the given lines.
Now,
b1→=i^+2j^-2k^ b2→=2i^+4j^-4k^
If θ is the angle between the given lines, then
cos θ=b1→.b2→b1→ b2→ =i^+2j^-2k^.2i^+4j^-4k^12+22+-22 22+42+-42 =2+8+83×6 =1⇒θ=0°
(ii) r→=3i^+2j^-4k^+λi^+2j^+2k^ and r→=5j^-2k^+μ3i^+2j^+6k^
Let b1→ and b2→ be vectors parallel to the given lines.
Now,
b1→=i^+2j^+2k^ b2→=3i^+2j^+6k^
If θ is the angle between the given lines, then
cos θ=b1→.b2→b1→ b2→ =i^+2j^+2k^.3i^+2j^+6k^12+22+22 32+22+62 =3+4+123×7 =1921⇒θ=cos-11921
(iii) r→=λi^+j^+2k^ and r→=2j^+μ3-1i^-3+1j^+4k^
Let b1→ and b2→ be vectors parallel to the given lines.
Now,
b1→=i^+j^+2k^ b2→=3-1i^-3+1j^+4k^
If θ is the angle between the given lines, then
cos θ=b1→.b2→b1→ b2→ =i^+j^+2k^.3-1i^-3+1j^+4k^12+12+22 3-12+3+12+42 =3-1-3+1+86 24 =612 =12⇒θ=π3
Q9.
Answer :
(i) x+43=y-15=z+34 and x+11=y-41=z-52
Let b1→ and b2→ be vectors parallel to the given lines.
b1→=3i^+5j^+4k^ b2→=i^+j^+2k^
If θ is the angle between the given lines, then
cos θ=b1→.b2→b1→ b2→ =3i^+5j^+4k^.i^+j^+2k^32+52+42 12+12+22 =3+5+8103 =853⇒θ=cos-1853
(ii) x-12=y-23=z-3-3 and x+3-1=y-58=z-14
Let b1→ and b2→ be vectors parallel to the given lines.
Now,
b1→=2i^+3j^-3k^ b2→=-i^+8j^+4k^
If θ is the angle between the given lines, then
cos θ=b1→.b2→b1→ b2→ =2i^+3j^-3k^.-i^+8j^+4k^22+32+-32 -12+82+42 =-2+24-12922 =10922⇒θ=cos-110922
(iii) 5-x-2=y+31=1-z3 and x3=1-y-2=z+5-1
The equations of the given lines can be re-written as
x-52=y+31=z-1-3 and x3=y-12=z+5-1
Let b1→ and b2→ be vectors parallel to the given lines.
Now,
b1→=2i^+j^-3k^ b2→=3i^+2j^-k^
If θ is the angle between the given lines, then
cos θ=b1→.b2→b1→ b2→ =2i^+j^-3k^.3i^+2j^-k^22+12+-32 32+22+-12 =6+2+314 14 =1114⇒θ=cos-11114
(iv) x-23=y+3-2, z=5 and x+11=2y-33=z-52
The equations of the given lines can be re-written as
x-23=y+3-2=z-50 and x+11=y-3232=z-52
Let b1→ and b2→ be vectors parallel to the given lines.
Now,
b1→=3i^-2j^+0k^ b2→=i^+32j^+2k^
If θ is the angle between the given lines, then
cos θ=b1→.b2→b1→ b2→ =3i^-2j^+0k^.i^+32j^+2k^32+-22+02 12+322+22 =3-3+013 294 =0⇒θ=π2
(v ) x-51=2y+6-2=z-31 and x-23=y+14=z-65
The equations of the given lines can be re-written as
x-51=y+3-1=z-31 and x-23=y+14=z-65
Let b1→ and b2→ be vectors parallel to the given lines.
Now,
b1→=i^-j^+k^b2→=3i^+4j^+5k^
If θ is the angle between the given lines, then
cos θ=b1→.b2→b1→ b2→ =i^-j^+k^.3i^+4j^+5k^12+-12+12 32+42+52 =3-4+53 50 =456⇒θ=cos-1456
Disclaimer: The answer given in the book is incorrect. This solution is created according to the question given in the book.
(vi) -x+2-2=y-17=z+3-3 and x+2-1=2y-84=z-54
The equations of the given lines can be re-written as
x-22=y-17=z+3-3 and x+2-1=y-42=z-54
Let b1→ and b2→ be vectors parallel to the given lines.
Now,
b1→=2i^+7j^-3k^ b2→=-1i^+2j^+4k^
If θ is the angle between the given lines, then
cos θ=b1→.b2→b1→ b2→ =2i^+7j^-3k^.-1i^+2j^+4k^22+72+-32 -12+22+42 =-2+14-1262 21 =0⇒θ=π2
Q10.
Answer :
(i) 5, −12, 13 and −3, 4, 5
Let m1→ and m2→ be vectors parallel to the two given lines. Then, the angle between the two given lines is same as the angle between m1 → and m2→.Now, m1→=Vector parallel to the line having direction ratios proportional to 5,-12, 13 m2→=Vector parallel to the line having direction ratios proportional to -3, 4, 5∴ m1→=5i^-12j^+13k^ m2→=-3i^+4j^+5k^Let θ be the angle between the lines.
Now,cos θ=m1→.m2→m1→ m2→ =5i^-12j^+13k^.-3i^+4j^+5k^52+-122+132 -32+42+52 =-15-48+65132×52 =165⇒θ=cos-1165
(ii) 2, 2, 1 and 4, 1, 8
Let m1→ and m2→ be vectors parallel to the given two lines . Then, the angle between the lines is same as the angle between m1 → and m2.→Now, m1→=Vector parallel to the line having direction ratios proportional to 2, 2, 1m2→=Vector parallel to the line having direction ratios proportional to 4, 1, 8∴ m1→=2i^-2j^+k^ m2→=4i^+j^+8k^Let θ be the angle between the lines.
Now,cos θ=m1→.m2→m1→ m2→ =2i^+2j^+k^.4i^+j^+8k^22+22+12 42+12+82 =8+2+83×9 =23⇒θ=cos-123
(iii) 1, 2, −2 and −2, 2, 1
Let m1→ and m2→ be vectors parallel to the two given lines. Then, the angle between the two given lines is same as the angle between m1 → and m2.→Now, m1→=Vector parallel to the line having direction ratios proportional to 1, 2, -2 m2→=Vector parallel to the line having direction ratios proportional to-2, 2, 1∴ m1→=i^+2j^-2k^ m2→=-2i^+2j^+k^Let θ be the angle between the lines.
Now,cos θ=m1→.m2→m1→ m2→ =i^+2j^-2k^.-2i^+2j^+k^12+22+-22 -22+22+12 =-2+4-23×3 =0⇒θ=π2
(iv) a, b, c and b − c, c − a, a − b.
Let m1→ and m2→ be vectors parallel to the given two lines. Then, the angle between the two lines is same as the angle between m1 → and m2→.Now, m1→=Vector parallel to the line having direction ratios proportional to a, b, cm2→=Vector parallel to the line having direction ratios proportional to b-c, c-a, a-b∴ m1→=ai^+bj^+ck^ and m2→=b-ci^+c-aj^+a-bk^Let θ be the angle between the lines.
Now,cos θ=m1→.m2→m1→ m2→ =ai^+bj^+ck^.b-ci^+c-aj^+a-bk^a2+b2+c2 b-c2+c-a2+a-b2 =ab-ac+bc-ba+ca-cba2+b2+c2 b-c2+c-a2+a-b2 =0⇒θ=π2
Q11.
Answer :
The direction ratios of the line joining the points (3, 1, 4) and (7, 2, 12) are proportional to 4, 1, 8.
Let m1→ and m2→ be vectors parallel to the lines having direction ratios proportional to 2, 2, 1 and 4, 1, 8.
Now,
b1→=2i^+2j^+k^ b2→=4i^+j^+8k^
If θ is the angle between the given lines, then
cos θ=m1→.m2→m1→ m2→ =2i^+2j^+k^.4i^+j^+8k^22+22+12 42+12+82 =8+2+83×9 =23⇒θ=cos-123
Q12.
Answer :
The direction ratios of the line parallel to line x-34=y-52=z+13 are proportional to 4, 2, 3.
Equation of the required line passing through the point (1, 2, -4) having direction ratios proportional to 4, 2, 3 is
x-14=y-22=z–43=x-14=y-22=z+43
Q13.
Answer :
The equation of line 2x-14=3y+52=2-z3 can be re-written as
x-122=y+5323=z-2-3
The direction ratios of the line parallel to line 2x-14=3y+52=2-z3 are proportional to 2, 23, -3.
Equation of the required line passing through the point (-1, 2, 1) having direction ratios proportional to 2, 23, -3 is
x–12=y-223=z-1-3=x+12=y-223=z-1-3
Q14.
Answer :
The given line is parallel to the vector 2i^+3j^-5k^ and the required line is parallel to the given line.
So, the required line is parallel to the vector 2i^+3j^-5k^.
Hence, the equation of the required line passing through the point (2,-1, 3) and parallel to the vector 2i^+3j^-5k^ is r→=2i^-j^+3k^+λ2i^+3j^-5k^.
Q15.
Answer :
Let:
b1→=i^+2j^+3k^ b2→=-3i^+2j^+5k^
Since the required line is perpendicular to the lines parallel to the vectors b1→=i^+2j^+3k^ and b2→=-3i^+2j^+5k^, it is parallel to the vector b→=b1→×b2→.
Now,
b→=b1→×b2→ =i^j^k^123-325 =4i^-14j^+8k^ =22i^-7j^+4k^
Thus, the direction ratios of the required line are proportional to 2, -7, 4.
The equation of the required line passing through the point (2, 1, 3) and having direction ratios proportional to 2, -7, 4 is x-22=y-1-7=z-34.
Q16.
Answer :
The required line is perpendicular to the lines parallel to the vectors b1→=2i^+j^-3k^ and b2→=i^+j^+k^.
So, the required line is parallel to the vector b→=b1→×b2→.
Now,
b→=b1→×b2→ =i^j^k^21-3111 =4i^-5j^+k^
Equation of the required line passing through the point i^+j^-3k^ and parallel to 4i^-5j^+k^ is r→=i^+j^-3k^+λ4i^-5j^+k^.
Q17.
Answer :
The direction ratios of the line joining the points (4, 3, 2), (1,-1, 0) and (1, 2, -1), (2, 1, 1) are -3, -4, -2 and 1, -1, 2, respectively.
Let:
b1→=-3i^-4j^-2k^ b2→=i^-j^+2k^
Since the required line is perpendicular to the lines parallel to the vectors b1→=-3i^-4j^-2k^ and b2→=i^-j^+2k^, it is parallel to the vector b→=b1→×b2→.
Now,
b→=b1→×b2→ =i^j^k^-3-4-21-12 =-10i^+4j^+7k^
So, the direction ratios of the required line are proportional to -10, 4, 7.
The equation of the required line passing through the point (1, -1, 1) and having direction ratios proportional to -10, 4, 7 is x-1-10=y+14=z-17.
Q18.
Answer :
We have
x-88=y+9-16=z-107x-153=y-298=z-5-5
Let:
b1→=8i^-16j^+7k^ b2→=3i^+8j^-5k^
Since the required line is perpendicular to the lines parallel to the vectors b1→=8i^-16j^+7k^ and b2→=3i^+8j^-5k^, it is parallel to the vector b→=b1→×b2→.
Now,
b→=b1→×b2→ =i^j^k^8-16738-5 =24i^+61j^+112k^
The direction ratios of the required line are proportional to 24, 61, 112.
The equation of the required line passing through the point (1, 2, -4) and having direction ratios proportional to 24, 61, 112 is x-124=y-261=z+4112.
Page 28.17 Ex. 28.2
Q19.
Answer :
The direction ratios of the lines x-57=y+2-5=z1 and x1=y2=z3 are proportional to 7, -5, 1 and 1, 2, 3, respectively.
Let:
b1→=7i^-5j^+k^ b2→=i^+2j^+3k^
Now,
b1→.b2→=7i^-5j^+k^.i^+2j^+3k^ =7-10+3 =0∴ b1→⊥b2→
Hence, the given lines are perpendicular to each other.
Q20.
Answer :
The equation of the line 6x − 2 = 3y + 1 = 2z − 2 can be re-written as
x-1316=y+1313=z-112= x-131=y+132=z-13
Since the required line is parallel to the given line, the direction ratios of the required line are proportional to 1, 2, 3.
The vector equation of the required line passing through the point (2, -1, -1) and having direction ratios proportional to 1, 2, 3 is r→=2i^-j^-k^+λi^+2j^+3k^.
Q21.
Answer :
The equations of the given lines are
x-1-3=y-22 λ=z-32x-13λ=y-11=z-6-5
Since the given lines are perpendicular to each other, we have
-33λ+2λ1+2-5=0⇒-9λ+2λ-10=0⇒λ=-107
Q22.
Answer :
The direction ratios of AB and CD are proportional to 3, 3, 4 and 6, 6, 8, respectively.
Let θ be the angle between AB and CD. Then,
cos θ=3×6+3×6+4×832+32+42 62+62+82 =6834 136 =1⇒θ=0°
Q23.
Answer :
The equations of the given lines x-55λ+2=2-y5=1-z-1 and x1=2y+14λ=1-z-3 can be re-written as
x-55λ+2=y-2-5=z-11 and x1=y+122λ=z-13
Since the given lines are perpendicular to each other, we have
5λ+21-52λ+13=0⇒5λ=5⇒λ=1
Answer :
(i) The equation of the plane passing through points (2, 1, 0), (3, −2, −2) and (3, 1, 7) is given by
x-2y-1z-03-2-2-1-2-03-21-17-0=0⇒x-2y-1z-01-3-2107=0⇒-21 x-2 – 9 y-1 + 3z = 0⇒-21x + 42 – 9y + 9 + 3z = 0⇒-21x – 9y + 3z + 51 = 0⇒21x + 9y – 3z = 51⇒7x + 3y – z = 17
(ii) The equation of the plane passing through points (−5, 0, −6), (−3, 10, −9) and (−2, 6, −6) is given by
x+5y-0 z+6-3+5 10-0-9+6-2+56-0-6+6 = 0⇒x+5yz+6210-3360 = 0⇒18 x+5 – 9y – 18 z+6 = 0⇒2 x+5 – y – 2 z+6 = 0⇒2x + 10 – y – 2z – 12 = 0⇒2x – y – 2z – 2 = 0
(iii) The equation of the plane passing through points (1, 1, 1), (1, −1, 2) and (−2, −2, 2) is given by
x-1y-1z-11-1-1-12-1-2-1-2-12-1=0⇒x-1y-1z-10-21-3-31=0⇒1 x-1-3 y-1-6 z-1 = 0⇒x – 1 – 3y + 3 – 6z + 6 = 0⇒x – 3y – 6z + 8 = 0
(iv) The equation of the plane passing through points (2, 3, 4), (−3, 5, 1) and (4, −1, 2) is given by
x-2y-3z-4-3-25-31-44-2-1-32-4=0⇒x-2y-3z-4-52-32-4-2=0⇒-16 x – 2 – 16 y – 3 + 16 z – 4 = 0⇒x – 2 + y – 3 – z – 4 = 0⇒x + y – z = 1
(v) The equation of the plane passing through points (0, −1, 0), (3, 3, 0) and (1, 1, 1) is given by
x-0y+1z-03-03+10-01-01+11-0=0⇒x-0y+1z-0340121=0⇒4x – 3 y + 1 + 2z = 0⇒4x – 3y + 2z = 3
Q1.
Answer :
The coordinates of any point on the first line are given by
x1=y-22=z+33=λ⇒x=λ y=2λ+2 z=3λ-3
The coordinates of a general point on the first line are λ, 2λ+2, 3λ-3.
Also, the coordinates of any point on the second line are given by
x-22=y-63=z-34=μ⇒x=2μ+2 y=3μ+6 z=4μ+3
The coordinates of a general point on the second line are 2μ+2, 3μ+6, 4μ+3
If the lines intersect, then they have a common point. So, for some values of λ and μ, we must have
λ=2μ+2, 2λ+2=3μ+6, 3λ-3=4μ+3⇒λ-2μ=2 …(1) 2λ-3μ=4 …(2) 3λ-4μ=6 …(3)Solving (1) and (2), we getλ=2 and μ=0Substituting λ=2 and μ=0 in (3), we getLHS=3λ-4μ =32-40 =6 =RHSSince λ=2 and μ=0 satisfy the third equation, the given lines intersect at 2, 6, 3.
Q2.
Answer :
The coordinates of any point on the first line are given by
x-13=y+12=z-15=λ⇒x=3λ+1 y=2λ-1 z=5λ+1
The coordinates of a general point on the first line are 3λ+1, 2λ-1, 5λ+1.
The coordinates of any point on the second line are given by
x+24=y-13=z+1-2=μ⇒x=4μ-2 y=3μ+1 z=-2μ-1
The coordinates of a general point on the second line are 4μ-2, 3μ+1, -2μ-1.
If the lines intersect, then they have a common point. So, for some values of λ and μ, we must have
3λ+1=4μ-2, 2λ-1=3μ+1, 5λ+1=-2μ-1⇒3λ-4μ=-3 …(1) 2λ-3μ=2 …(2) 5λ+2μ=-2 …(3)Solving (1) and (2), we getλ=-17 μ=-12Substituting λ=-17 and μ=-12 in (3), we getLHS=3λ+2μ =3-17+2-12 =-75 ≠-2⇒LHS≠RHSHence, the given lines do not intersect.
Q3.
Answer :
The coordinates of any point on the first line are given by
x+13=y+35=z+57=λ⇒x=3λ-1 y=5λ-3 z=7λ-5
The coordinates of a general point on the first line are 3λ-1, 5λ-3, 7λ-5.
The coordinates of any point on the second line are given by
x-21=y-43=z-65=μ⇒x=μ+2 y=3μ+4 z=5μ+6
The coordinates of a general point on the second line are μ+2, 3μ+4, 5μ+6.
If the lines intersect, then they have a common point. So, for some values of λ and μ, we must have
3λ-1=μ+2, 5λ-3=3μ+4, 7λ-5=5μ+6⇒3λ-μ=3 …(1) 5λ-3μ=7 …(2) 7λ-5μ=11 …(3)Solving (1) and (2), we getλ=12 μ=-32Substituting λ=12 and μ=-32 in (3), we getLHS=7λ-5μ =712-5-32 =11 =RHSSince λ=12 and μ=-32 satisfy (3), the given lines intersect.Substituting the value of λ in the general coordinates of the first line, we getx=12y=-12z=-32Hence, the given lines intersect at point 12, -12, -32.
Q4.
Answer :
The coordinates of any point on the line AB are given by
x-04-0=y+15+1=z+11+1=λ⇒x=4λ y=6λ-1 z=2λ-1
The coordinates of a general point on AB are 4λ, 6λ-1, 2λ-1.
The coordinates of any point on the line CD are given by
x-33+4=y-99-4=z-44-4=μ⇒x=7μ+3 y=5μ+9 z=4
The coordinates of a general point on CD are 7μ+3, 5μ+9, 4.
If the lines AB and CD intersect, then they have a common point. So, for some values of λ and μ, we must have
4λ=7μ+3, 6λ-1=5μ+9, 2λ-1=4⇒4λ-7μ=3 …(1) 6λ-5μ=10 …(2) λ=52 …(3)Solving (2) and (3), we getλ=52 μ=1Substituting λ=52 and μ=1 in (1), we getLHS=4λ-7μ =452-71 =3 =RHSSince λ=52 and μ=1 satisfy (3), the given lines intersect.Substituting the value of λ in the coordinates of a general point on the line AB, we getx=10y=14 z=4Hence, AB and CD intersect at point 10, 14, 4.
Q5.
Answer :
The position vectors of two arbitrary points on the given lines are
i^+j^-k^+λ3i^-j^=1+3λi^+ 1-λj^-k^4i^-k^+μ2i^+3k^=4+2μi^+0j^+3μ-1k^
If the lines intersect, then they have a common point. So, for some values of λ and μ, we must have
1+3λi^+ 1-λj^-k^=4+2μi^+0j^+3μ-1k^
Equating the coefficients of i^, j^ and k^, we get
1+3λ=4+2μ …(1)1-λ=0 …(2)3μ-1=-1 …(3)
Solving (2) and (3), we get
λ=1 μ=0
Substituting the values λ=1 and μ=0 in (1), we get
LHS=1+3λ =1+31 =4RHS=4+2μ =4+20 =4⇒LHS=RHSSince λ=1 and μ=0 satisfy (3), the given lines intersect.
Substituting μ=0 in the second line, we get r→=4i^+0j^-k^ as the position vector of the point of intersection.
Thus, the coordinates of the point of intersection are (4, 0, -1).
Q6.
Answer :
(i) r→=i^-j^+λ2i^+k^ and r→=2i^-j^+μi^+j^-k^
The position vectors of two arbitrary points on the given lines are
i^-j^+λ2i^+k^=1+2λ i^ -j^+λk^2i^-j^+μi^+j^-k^=2+μ i^+-1+μ j^-μk^
If the lines intersect, then they have a common point. So, for some values of λ and μ, we must have
1+2λi^+ -j^+λk^=2+μi^+-1+μj^-μk^
Equating the coefficients of i^, j^ and k^, we get
1+2λ=2+μ …(1)-1=-1+μ …(2) λ=-μ …(3)
Solving (2) and (3), we get
λ=0 μ=0.
Substituting the values λ=0 and μ=0 in (1), we get
LHS=1+2λ =1+20 =1RHS=2+μ =2+0 =2⇒LHS≠RHSSince λ=0 and μ=0 do not satisfy (1), the given lines do not intersect.
(ii) x-12=y+13=z and x+15=y-21; z=2
The coordinates of any point on the first line are given by
x-12=y+13=z=λ⇒x=2λ+1 y=3λ-1 z=λ
The coordinates of a general point on the first line are 2λ+1, 3λ-1, λ.
Also, the coordinates of any point on the second line are given by
x+15=y-21=μ, z=2⇒x=5μ-1 y=μ+2 z=2
The coordinates of a general point on the second line are 5μ-1, μ+2, 2.
If the lines intersect, then they have a common point. So, for some values of λ and μ, we must have
2λ+1=5μ-1, 3λ-1=μ+2, λ=2⇒ 2λ-5μ=-2 …(1) 3λ-μ=3 …(2) λ=2 …(3)Solving (2) and (3), we getλ=2 μ=3Substituting λ=2 and μ=3 in 1, we getLHS=2λ-5μ =22-53 =4-15 =-11≠-2⇒LHS≠RHSSince λ=2 and μ=3 do not satisfy (1), the given lines do not intersect.
(iii) x-13=y-1-1=z+10 and x-42=y-00=z+13
The coordinates of any point on the first line are given by
x-13=y-1-1=z+10=λ⇒x=3λ+1 y=-λ+1 z=-1
The coordinates of a general point on the first line are 3λ+1, -λ+1, -1.
Also, the coordinates of any point on the second line are given by
x-42=y-00=z+13=μ⇒x=2μ+4 y=0 z=3μ-1
The coordinates of a general point on the second line are 2μ+4, 0, 3μ-1.
If the lines intersect, then they have a common point. So, for some values of λ and μ, we must have
3λ+1=2μ+4, -λ+1=0, -1=3μ-1⇒3λ-2μ=3 …(1) λ=1 …(2) μ=0 …(3)From (2) and (3), we getλ=1μ=0Substituting λ=1 and μ=0 in (1), we getLHS=3λ-2μ =31-20 =3 =RHSSince λ=1 and μ=0 satisfy (1), the lines intersect.Substituting λ=1 and μ=0 in the coordinates of a general point on the first line, we getx=4y=0 z=-1Hence, the given lines intersect at 4, 0, -1.
(iv) x-54=y-74=z+3-5 and x-87=y-41=z-53
The coordinates of any point on the first line are given by
x-54=y-74=z+3-5=λ⇒x=4λ+5 y=4λ+7 z=-5λ-3
The coordinates of a general point on the first line are 4λ+5, 4λ+7, -5λ-3.
The coordinates of any point on the second line are given by
x-87=y-41=z-53=μ⇒x=7μ+8 y=μ+4 z=3μ+5
The coordinates of a general point on the second line are 7μ+8, μ+4, 3μ+5.
If the lines intersect, then they have a common point. So, for some values of λ and μ, we must have
4λ+5=7μ+8, 4λ+7=μ+4, -5λ-3=3μ+5⇒4λ-7μ=3 …(1) 4λ-μ=-3 …(2) 5λ+3μ=-8 …(3)From (1) and (2), we getλ=-1 μ=-1Substituting λ=-1 and μ=-1 in (3), we getLHS=5λ+3μ =5-1+3-1 =-8 =RHSSince λ=-1 and μ=-1 satisfy (3), the lines intersect.Substituting λ=-1 and μ=-1 in the coordinates of a general point on the first line, we getx=1y=3z=2Hence, the given lines intersect at 1, 3, 2.
Q7.
Answer :
The position vectors of two arbitrary points on the given lines are
3i^+2j^-4k^+λi^+2j^+2k^=3+λi^+ 2+2λj^+2λ-4k^5i^-2j^+μ3i^+2j^+6k^=5+3μi^+-2+2μj^+6μk^
If the lines intersect, then they have a common point. So, for some values of λ and μ, we must have
3+λi^+ 2+2λj^+2λ-4k^=5+3μi^+-2+2μj^+6μk^
Equating the coefficients of i^, j^ and k^, we get
3+λ=5+3μ …(1)2+2λ=-2+2μ …(2) 2λ-4=6μ …(3)
Solving (1) and (2), we get
λ=-4μ=-2.
Substituting the values λ=-4 and μ=-2 in (3), we get
LHS=2λ-4 =2-4-4 =-12RHS=6μ =6-2 =-12⇒LHS=RHSSince λ=-4 and μ=-2 satisfy (3), the lines intersect.
Substituting μ=-2 in the second line, we get r→=5i^-2j^-6i^-4j^-12k^=-i^-6j^-12k^ as the position vector of the point of intersection.
Thus, the coordinates of the point of intersection are (-1, -6, -12).
Page 28.28 Ex. 28.4
Q1.
Answer :
Let the point (3, -1, 11) be P and the point through which the line passes be Q (0, 2, 3).
The line is parallel to the vector b→=2i^-3j^+4k^.
Now,
PQ→=-3i^+3j^-8k^
∴ b→×PQ→=i^j^k^2-34-33-8 =12i^+4j^+15k^⇒b→×PQ→=122+42+152 =144+16+225 =385d=b→×PQ→b→ =38529 =38529
Q2.
Answer :
Let the point (1, 0, 0) be P and the point through which the line passes be Q (1, -1, -10).
The line is parallel to the vector b→=2i^-3j^+8k^.
Now,
PQ→=0i^-j^-10k^
∴ b→×PQ→=i^j^k^2-380-1-10 =38i^+20j^-2k^⇒b→×PQ→=382+202+22 =1444+400+4 =1848d=b→×PQ→b→ =184877 =24 =26
Let L be the foot of the perpendicular drawn from the point P (1, 0, 0) to the given line.
The coordinates of a general point on the line x-12=y+1-3=z+108 are given by
x-12=y+1-3=z+108=λ⇒x=2λ+1 y=-3λ-1 z=8λ-10
Let the coordinates of L be 2λ+1, -3λ-1, 8λ-10.
The direction ratios of PL are proportional to 2λ+1-1, -3λ-1-0, 8λ-10-0, i.e. 2λ, -3λ-1, 8λ-10.
The direction ratios of the given line are proportional to 2 ,-3, 8, but PL is perpendicular to the given line.
∴ 22λ-3-3λ-1+88λ-10=0⇒λ=1
Substituting λ=1 in 2λ+1, -3λ-1, 8λ-10, we get the coordinates of L as (3, -4, -2).
Equation of the line PL is given by
x-13-1=y-0-4-0=z-0-2-0=x-11=y-2=z-1
⇒r→=i^+λi^-2j^-k^
Q3.
Answer :
Let D be the foot of the perpendicular drawn from the point A (1, 0, 3) to the line BC.
The coordinates of a general point on the line BC are given by
x-44-3=y-77-5=z-11-3=λ⇒x=λ+4 y=2λ+7 z=-2λ+1
Let the coordinates of D be λ+4, 2λ+7, -2λ+1.
The direction ratios of AD are proportional to λ+4-1, 2λ+7-0, -2λ+1-3, i.e. λ+3, 2λ+7, -2λ-2.
The direction ratios of the line BC are proportional to 1, 2, -2, but AD is perpendicular to the line BC.
∴1λ+3+22λ+7-2-2λ-2=0⇒λ=-73
Substituting λ=-73 in λ+4, 2λ+7, -2λ+1, we get the coordinates of D as 53, 73, 173.
Q4.
Answer :
Point D is the foot of the perpendicular drawn from the point A (1, 0, 4) to the line BC.
The coordinates of a general point on the line BC are given by
x-02-0=y+11-3+11=z-31-3=λ⇒x=2λ y=8λ-11 z=-2λ+3
Let the coordinates of D be 2λ, 8λ-11, -2λ+3.
The direction ratios of AD are proportional to 2λ-1, 8λ-11-0, -2λ+3-4, i.e. 2λ-1, 8λ-11, -2λ-1.
The direction ratios of the line BC are proportional to 2, 8,-2, but AD is perpendicular to the line BC.
∴ 22λ-1+88λ-11-2-2λ-1=0⇒λ=119
Substituting λ=119 in 2λ, 8λ-11, -2λ+3, we get the coordinates of D as 229, -119, 59.
Q5.
Answer :
Let L be the foot of the perpendicular drawn from the point P (2, 3, 4) to the given line.
The coordinates of a general point on the line 4-x2=y6=1-z3 are given by
4-x2=y6=1-z3=λThey can be re-written as x-4-2=y6=z-1-3=λ⇒x=-2λ+4 y=6λ z=-3λ+1
Let the coordinates of L be -2λ+4, 6λ, -3λ+1.
The direction ratios of PL are proportional to -2λ+4-2, 6λ-3, -3λ+1-4, i.e. -2λ+2, 6λ-3, -3λ-3.
The direction ratios of the given line are proportional to -2, 6, -3, but PL is perpendicular to the given line.
∴-2-2λ+2+66λ-3-3-3λ-3=0⇒λ=1349
Substituting λ=1349 in -2λ+4, 6λ, -3λ+1, we get the coordinates of L as 17049, 7849, 1049.
∴ PL=17049-22+7849-32+1049-42 =445412401 =90949 =37101 .
Hence, the length of the perpendicular from P on PL is 37101 units.
Q6.
Answer :
Let L be the foot of the perpendicular drawn from the point P (2, 4, -1) to the given line.
The coordinates of a general point on the line x+51=y+34=z-6-9 are given by
x+51=y+34=z-6-9=λ⇒x=λ-5 y=4λ-3 z=-9λ+6
Let the coordinates of L be λ-5, 4λ-3, -9λ+6.
The direction ratios of PL are proportional to λ-5-2, 4λ-3-4, -9λ+6+1, i.e. λ-7, 4λ-7, -9λ+7.
The direction ratios of the given line are proportional to 1, 4, -9, but PL is perpendicular to the given line.
∴1λ-7+44λ-7-9-9λ+7=0⇒λ=1
Substituting λ=1 in λ-5, 4λ-3, -9λ+6, we get the coordinates of L as -4, 1, -3.
Equation of the line PL is
x-2-4-2=y-41-4=z+1-3+1=x-2-6=y-4-3=z+1-2
Q7.
Answer :
Let the point (5, 4, -1) be P and the the point through which the line passes be Q (1, 0, 0).
The line is parallel to the vector b→=2i^+9j^+5k^.
Now,
PQ→=-4i^-4j^+k^
∴ b→×PQ→=i^j^k^295-4-41 =29i^-22j^+28k^⇒b→×PQ→=292+-222+282 =841+484+784 =2109b→=22+92+52 =4+81+25 =110d=b→×PQ→b→ =2109110 =2109110
Q8.
Answer :
Let L be the foot of the perpendicular drawn from the point P (i^+6j^+3k^) to the line r→=j^+2k^+λi^+2j^+3k^.
Let the position vector L be
r→=j^+2k^+λi^+2j^+3k^=λi^+1+2λj^+2+3λk^ …(1)
Now,
PL→=Position vector of L- Position vector of P⇒PL→=λi^+1+2λj^+2+3λk^-i^+6j^+3k^⇒PL→=λ-1i^+2λ-5j^+3λ-1k^ …(2)
Since PL→ is perpendicular to the given line, which is parallel to b→=i^+2j^+3k^, we have
PL→.b→=0⇒λ-1i^+2λ-5j^+3λ-1k^.i^+2j^+3k^=0 ⇒1λ-1+22λ-5+33λ-1=0⇒λ=1
Substituting λ=1 in (1), we get the position vector of L as i^+3j^+5k^.
Substituting λ=1 in (2), we get
PL→=-3j^+2k^
=-32+22 =13
Hence, the length of the perpendicular from point P on PL is 13 units.
Q9.
Answer :
Let L be the foot of the perpendicular drawn from the point P (-1, 3, 2) to the line r→=2j^+3k^+λ2i^+j^+3k^.
Let the position vector L be
r→=2j^+3k^+λ2i^+j^+3k^=2λi^+2+λj^+3+3λk^ …(1)
Now,
PL→=Position vector of L- Position vector of P⇒PL→=2λi^+2+λj^+3+3λk^–i^+3j^+2k^⇒PL→=2λ+1i^+λ-1j^+3λ+1k^ …(2)
Since PL→ is perpendicular to the given line, which is parallel to b→=2i^+j^+3k^, we have
PL→.b→=0⇒2λ+1i^+λ-1j^+3λ+1k^.2i^+j^+3k^=0 ⇒22λ+1+1λ-1+33λ+1=0⇒λ=-27
Substituting λ=-27 in (1), we get the position vector of L as -47i^+127j^+157k^.
So, the coordinates of the foot of the perpendicular from P to the given line is L -47, 127, 157.
Substituting λ=-27 in (2), we get
PL→=37i^-97j^+17k^
Equation of the perpendicular drawn from P to the given line is
r→=Position vector of P +λPL→ =-i^+3j^+2k^ +λ3i^-9j^+k^
Q10.
Answer :
Let L be the foot of the perpendicular drawn from the point P (0, 2, 7) to the given line.
The coordinates of a general point on the line x+2-1=y-13=z-3-2 are given by
x+2-1=y-13=z-3-2=λ⇒x=-λ-2 y=3λ+1 z=-2λ+3
Let the coordinates of L be -λ-2, 3λ+1, -2λ+3.
The direction ratios of PL are proportional to -λ-2-0, 3λ+1-2, -2λ+3-7, i.e. -λ-2, 3λ-1, -2λ-4.
The direction ratios of the given line are proportional to -1, 3, -2, but PL is perpendicular to the given line.
∴-1-λ-2+33λ-1-2-2λ-4=0⇒λ=-12
Substituting λ=-12 in -λ-2, 3λ+1, -2λ+3, we get the coordinates of L as -32, -12, 4.
Q11.
Answer :
Let L be the foot of the perpendicular drawn from the point P (1, 2, -3) to the given line.
The coordinates of a general point on the line x+12=y-3-2=z-1 are given by
x+12=y-3-2=z-1=λ⇒x=2λ-1 y=-2λ+3 z=-λ
Let the coordinates of L be 2λ-1, -2λ+3 , -λ.
The direction ratios of PL are proportional to 2λ-1-1, -2λ+3-2, -λ+3, i.e. 2λ-2, -2λ+1, -λ+3.
The direction ratios of the given line are proportional to 2, -2, -1, but PL is perpendicular to the given line.
∴ 22λ-2-2-2λ+1-1-λ+3=0⇒λ=1
Substituting λ=1 in 2λ-1, -2λ+3 , -λ, we get the coordinates of L as 1, 1, -1.
Q12.
Answer :
Equation of line AB passing through the points A(0, 6,-9) and B(-3, -6, 3) is
x-0-3-0=y-6-6-6=z+93+9=x1=y-64=z+9-4
Here, D is the foot of the perpendicular drawn from C (7, 4, -1) on AB.
The coordinates of a general point on AB are given by
x1=y-64=z+9-4=λ⇒x=λ y=4λ+6 z=-4λ-9
Let the coordinates of D be λ, 4λ+6, -4λ-9.
The direction ratios of CD are proportional to λ-7, 4λ+6-4, -4λ-9+1, i.e. λ-7, 4λ+2, -4λ-8.
The direction ratios of AB are proportional to 1, 4, -4, but CD is perpendicular to AB.
Substituting λ=-1 in λ, 4λ+6, -4λ-9, we get the coordinates of D as -1, 2, -5.
Equation of CD is
x-7-1-7=y-42-4=z+1-5+1=x-74=y-41=z+12
Page 28.35 Ex. 28.5
Q1.
Answer :
(i) r→=3i^+8j^+3k^+λ3i^-j^+k^ and r→=-3i^-7j^+6k^+μ-3i^+2j^+4k^
Comparing the given equations with the equations r→=a1→+λb1→ and r→=a2→+μb2→, we get
a1→=3i^+8j^+3k^a2→=-3i^-7j^+6k^b1→=3i^-j^+k^ b2→=-3i^+2j^+4k^∴ a2→- a1→=-6i^-15j^+3k^and b1→×b2→=i^j^k^3-11-324 =-6i^-15j^+3k^⇒ b1→×b2→=-62+-152+32 =36+225+9 =270a2→- a1→.b1→×b2→=-6i^-15j^+3k^.-6i^-15j^+3k^ =36+225+9 =270
The shortest distance between the lines r→=a1→+λb1→ and r→=a2→+μb2→ is given by
d=a2→- a1→.b1→×b2→ b1→×b2→ =270270 =270
(ii) r→=3i^+5j^+7k^+λi^-2j^+7k^ and r→=-i^-j^-k^+μ7i^-6j^+k^
Comparing the given equations with the equations r→=a1→+λb1→ and r→=a2→+μb2→, we get
a1→=3i^+5j^+7k^a2→=-i^-j^-k^b1→=i^-2j^+7k^b2→=7i^-6j^+k^∴ a2→- a1→=-4i^-6j^-8k^and b1→×b2→=i^j^k^1-277-61 =40i^+48j^+8k^⇒ b1→×b2→=402+482+82 =1600+2304+64 =3968a2→- a1→.b1→×b2→=-4i^-6j^-8k^.40i^+48j^+8k^ =-160-288-64 =-512
The shortest distance between the lines r→=a1→+λb1→ and r→=a2→+μb2→ is given by
d=a2→- a1→.b1→×b2→ b1→×b2→ =-5123968 =5123968
(iii) r→=i^+2j^+3k^+λ2i^+3j^+4k^ and r→=2i^+4j^+5k^+μ3i^+4j^+5k^
Comparing the given equations with the equationsr→=a1→+λb1→ and r→=a2→+μb2→, we get
a1→=i^+2j^+3k^a2→=2i^+4j^+5k^b1→=2i^+3j^+4k^ b2→=3i^+4j^+5k^∴ a2→- a1→=i^+2j^+2k^and b1→×b2→=i^j^k^234345 =-i^+2j^-k^⇒ b1→×b2→=-12+22+-12 =1+4+1 =6a2→- a1→.b1→×b2→=i^+2j^+2k^.-i^+2j^-k^ =-1+4-2 =1
The shortest distance between the lines r→=a1→+λb1→ and r→=a2→+μb2→ is given by
d=a2→- a1→.b1→×b2→ b1→×b2→ =16 =16
(iv) r→=1-t i^+t-2 j^+3-t k^ and r→=s+1 i^+2s-1 j^-2s+1 k^
The vector equations of the given lines can be re-written as
r→=i^-2j^+3k^+t-i^+j^-k^ and r→=i^-j^-k^+si^+2j^-2k^
Comparing the given equations with the equations r→=a1→+λb1→ and r→=a2→+μb2→, we get
a1→=i^-2j^+3k^a2→=i^-j^-k^b1→=-i^+j^-k^ b2→=i^+2j^-2k^∴ a2→- a1→=j^-4k^and b1→×b2→=i^j^k^-11-112-2 =-3j^-3k^⇒ b1→×b2→=-32+-32 =9+9 =32a2→- a1→.b1→×b2→=j^-4k^.-3j^-3k^ =-3+12 =9
The shortest distance between the line r→=a1→+λb1→ and r→=a2→+μb2→ is given by
d=a2→- a1→.b1→×b2→ b1→×b2→ =932 =32
(v) r→=λ-1 i^+λ+1 j^-1+λ k^ and r→=1-μ i^+2μ-1 j^+μ+2 k^
The vector equations of the given lines can be re-written as
r→=-i^+j^-k^+λi^+j^-k^ and r→=i^-j^+2k^+μ-i^+2j^+k^
Comparing the given equations with the equations r→=a1→+λb1→ and r→=a2→+μb2→, we get
a1→=-i^+j^-k^a2→=i^-j^+2k^b1→=i^+j^-k^b2→=-i^+2j^+k^∴ a2→- a1→=2i^-2j^+3k^and b1→×b2→=i^j^k^11-1-121 =3i^+3k^⇒ b1→×b2→=32+32 =9+9 =32a2→- a1→.b1→×b2→=2i^-2j^+3k^.3i^+3k^ =6+9 =15
The shortest distance between the lines r→=a1→+λb1→ and r→=a2→+μb2→ is given by
d=a2→- a1→.b1→×b2→ b1→×b2→ =1532 =52
(vi) r→=2i^-j^-k^+λ2i^-5j^+2k^ and, r→=i^+2j^+k^+μi^-j^+k^
Comparing the given equations with the equations r→=a1→+λb1→ and r→=a2→+μb2→, we get
a1→=2i^-j^-k^a2→=i^+2j^+k^b1→=2i^-5j^+2k^ b2→=i^-j^+k^∴ a2→- a1→=-i^+3j^+2k^and b1→×b2→=i^j^k^2-521-11 =-3i^+3k^⇒ b1→×b2→=-32+32 =9+9 =32a2→- a1→.b1→×b2→=-i^+3j^+2k^.-3i^+3k^ =3+6 =9
The shortest distance between the lines r→=a1→+λb1→ and r→=a2→+μb2→ is given by
d=a2→- a1→.b1→×b2→ b1→×b2→ =932 =32
(vii) r→=i^+j^+λ2i^-j^+k^ and, r→=2i^+j^-k^+μ3i^-5j^+2k^
Comparing the given equations with the equations rer→=a1→+λb1→ and r→=a2→+μb2→, we get
a1→=i^+j^a2→=2i^+j^-k^b1→=2i^-j^+k^b2→=3i^-5j^+2k^∴ a2→- a1→=i^-k^and b1→×b2→=i^j^k^2-113-52 =3i^-j^-7k^⇒ b1→×b2→=32+-12+-72 =9+1+49 =59a2→- a1→.b1→×b2→=i^-k^.3i^-j^-7k^ =3+7 =10
The shortest distance between the lines r→=a1→+λb1→ and r→=a2→+μb2→ is given by
d=a2→- a1→.b1→×b2→ b1→×b2→ =1059 =1059
Page 28.36 Ex. 28.5
Q2.
Answer :
(i) The equations of the given lines are
x-12=y-23=z-34 …(1) x-23=y-34=z-55 …(2)
Since line (1) passes through the point (1, 2, 3) and has direction ratios proportional to 2, 3, 4, its vector equation is
r→=a1→+λb1→ Here,a1→=i^+2j^+3k^ b1→=2i^+3j^+4k^
Also, line (2) passes through the point (2, 3, 5) and has direction ratios proportional to 3, 4, 5.
Its vector equation is
r→=a2→+μb2→ Here,a2→=2i^+3j^+5k^ b2→=3i^+4j^+5k^
Now,
a2→- a1→=i^+j^+2k^and b1→×b2→=i^j^k^234345 =-i^+2j^-k^⇒ b1→×b2→=-12+22+-12 =1+4+1 =6and a2→- a1→.b1→×b2→=i^+j^+2k^.-i^+2j^-k^ =-1+2-2 =-1
The shortest distance between the lines r→=a1→+λb1→ and r→=a2→+μb2→ is given by
d=a2→- a1→.b1→×b2→ b1→×b2→ =-16 =16
(ii) The equations of the given lines are
x-12=y+13=z-01 …(1) x+13=y-21=z-20 …(2)
Since line (1) passes through the point (1, -1, 0) and has direction ratios proportional to 2, 3, 1, its vector equation is
r→=a1→+λb1→ Here,a1→=i^-j^+0k^ b1→=2i^+3j^+k^
Also, line (2) passes through the point (-1, 2, 2) and has direction ratios proportional to 3, 1, 0.
Its vector equation is
r→=a2→+μb2→ Here,a2→=-i^+2j^+2k^ b2→=3i^+j^+0k^
Now,
a2→- a1→=-2i^+3j^+2k^and b1→×b2→=i^j^k^231310 =-i^+3j^-7k^⇒ b1→×b2→=-12+32+-72 =1+9+49 =59and a2→- a1→.b1→×b2→=-2i^+3j^+2k^.-i^+3j^-7k^ =2+9-14 =-3
The shortest distance between the lines r→=a1→+λb1→ and r→=a2→+μb2→ is given by
d=a2→- a1→.b1→×b2→ b1→×b2→ =-359 =359
Disclaimer: The answer given in the book is incorrect. This solution is created according to the question given in the book.
(iii) x-1-1=y+21=z-3-2 …(1) x-11=y+12=z+1-2 …(2)
Since line (1) passes through the point (1, -2, 3) and has direction ratios proportional to -1, 1, -2, its vector equation is
r→=a1→+λb1→ Here,a1→=i^-2j^+3k^ b1→=-i^+j^-2k^
Also, line (2) passes through the point (1, -1, -1) and has direction ratios proportional to 1, 2, -2.
Its vector equation is
r→=a2→+μb2→ Here,a2→=i^-j^-k^b2→=i^+2j^-2k^
Now,
a2→- a1→=j^-4k^and b1→×b2→=i^j^k^-11-212-2 =2i^-4j^-3k^⇒ b1→×b2→=22+-42+-32 =4+16+9 =29a2→- a1→.b1→×b2→=j^-4k^.2i^-4j^-3k^ =-4+12 =8
The shortest distance between the lines r→=a1→+λb1→ and r→=a2→+μb2→ is given by
d=a2→- a1→.b1→×b2→ b1→×b2→ =829 =829
(iv) x-31=y-5-2=z-71 …(1) x+17=y+1-6=z+11 …(2)
Since line (1) passes through the point (3, 5, 7) and has direction ratios proportional to 1, -2, 1, its vector equation is
r→=a1→+λb1→ Here,a1→=3i^+5j^+7k^ b1→=i^-2j^+k^
Also, line (2) passes through the point (-1, -1, -1) and has direction ratios proportional to 7, -6, 1.
Its vector equation is
r→=a2→+μb2→ Here,a2→=-i^-j^-k^ b2→=7i^-6j^+k^
Now,
a2→- a1→=-4i^-6j^-8k^and b1→×b2→=i^j^k^1-217-61 =4i^+6j^+8k^⇒ b1→×b2→=42+62+82 =16+36+64 =116a2→- a1→.b1→×b2→=-4i^-6j^-8k^.4i^+6j^+8k^ =-16-36-64 =-116
The shortest distance between the lines r→=a1→+λb1→ and r→=a2→+μb2→ is given by
d=a2→- a1→.b1→×b2→ b1→×b2→ =-116116 =116 =229
Q3.
Answer :
(i) r→=i^-j^+λ2i^+k^ and r→=2i^-j^+μi^+j^-k^
Comparing the given equations with the equations r→=a1→+λb1→ and r→=a2→+μb2→, we get
a1→=i^-j^a2→=2i^-j^b1→=2i^+k^ b2→=i^+j^-k^∴ a2→- a1→=i^and b1→×b2→=i^j^k^20111-1 =-i^+3j^+2k^a2→- a1→.b1→×b2→=i^.-i^+3j^+2k^ =-1We observea2→- a1→.b1→×b2→≠0Thus, the given lines do not intersect.
(ii) r→=i^+j^-k^+λ3i^-j^ and r→=4i^-k^+μ2i^+3k^
Comparing the given equations with the equations r→=a1→+λb1→ and r→=a2→+μb2→, we get
a1→=i^+j^-k^a2→=4i^-k^b1→=3i^-j^ b2→=2i^+3k^∴ a2→- a1→=3i^-j^and b1→×b2→=i^j^k^3-10203 =-3i^-9j^+2k^a2→- a1→.b1→×b2→=3i^-j^.-3i^-9j^+2k^ =-9+9 =0We observea2→- a1→.b1→×b2→=0Thus, the given lines intersect.
(iii) x-12=y+13=z-01 and x+15=y-21=z-20
Since the first line passes through the point (1, -1, 0) and has direction ratios proportional to 2, 3, 1, its vector equation is
r→=a1→+λb1→ …(1) Here,a1→=i^-j^+0k^ b1→=2i^+3j^+k^
Also, the second line passes through the point (-1, 2, 2) and has direction ratios proportional to 5, 1, 0.
Its vector equation is
r→=a2→+μb2→ …(2) Here, a2→=-i^+2j^+2k^ b2→=5i^+j^+0k^
Now,
a2→- a1→=-2i^+3j^+2k^and b1→×b2→=i^j^k^231510 =-i^+5j^-13k^a2→- a1→.b1→×b2→=-2i^+3j^+2k^.-i^+5j^-13k^ =2+15-26 =-9We observea2→- a1→.b1→×b2→≠0Thus, the given lines do not intersect.
(iv) x-54=y-7-5=z+3-5 and x-87=y-71=z-53
Since the first line passes through the point (5, 7, -3) and has direction ratios proportional to 4, -5, -5, its vector equation is
r→=a1→+λb1→ …(1) Here,a1→=5i^+7j^-3k^ b1→=4i^-5j^-5k^
Also, the second line passes through the point (8, 7, 5) and has direction ratios proportional to 7, 1, 3.
Its vector equation is
r→=a2→+μb2→ … (2) Here,a2→=8i^+7j^+5k^ b2→=7i^+j^+3k^
Now,
a2→- a1→=3i^+8k^and b1→×b2→=i^j^k^4-5-5713 =-10i^-47j^+39k^a2→- a1→.b1→×b2→=3i^+8k^.-10i^-47j^+39k^ =-30+312 =282We observea2→- a1→.b1→×b2→≠0Thus, the given lines do not intersect.
Q4.
Answer :
(i) The vector equations of the given lines are
r→=i^+2j^+3k^+λi^-j^+k^ …(1)r→=2i^-j^-k^+μ-i^+j^-k^ =2i^-j^-k^-μi^-j^+k^ …(2)
These two lines pass through the points having position vectors a1→=i^+2j^+3k^ and a2→=2i^-j^-k^ and are parallel to the vector b→=i^-j^+k^.
Now,
a2→-a1→=i^-3j^-4k^
and
a2→-a1→×b→=i^-3j^-4k^×i^-j^+k^ =i^j^k^1-3-41-11 =-7i^-5j^+2k^⇒a2→-a1→×b→=-72+-52+22 =49+25+4 =78
The shortest distance between the two lines is given by
a2→-a1→×b→b→=783=26
(ii) r→=i^+j^+λ2i^-j^+k^ and r→=2i^+j^-k^+μ4i^-2j^+2k^ or r→=2i^+j^-k^+2μ2i^-j^+k^
These two lines pass through the points having position vectors a1→=i^+j^ and a2→=2i^+j^-k^ and are parallel to the vector b→=2i^-j^+k^.
Now,
a2→-a1→=i^-k^
and
a2→-a1→×b→=i^-k^×2i^-j^+k^ =i^j^k^10-12-11 =-i^-3j^-k^⇒a2→-a1→×b→=-12+-32+-12 =1+9+1 =11
The shortest distance between the two lines is given by
a2→-a1→×b→b→=116
Q5.
Answer :
(i) The equation of the line passing through the points (0, 0, 0) and (1, 0, 2) is
x-01-0=y-00-0=z-02-0=x1=y0=z2
(ii) The equation of the line passing through the points (1, 3, 0) and (0, 3, 0) is
x-10-1=y-33-3=z-00-0=x-1-1=y-30=z0
Since the first line passes through the point (0, 0, 0) and has direction ratios proportional to 1, 0, 2, its vector equation is
r→=a1→+λb1→ …(1) Here,a1→=0i^+0j^+0k^ b1→=i^+0j^+2k^
Also, the second line passes through the point (1, 3, 0) and has direction ratios proportional to -1, 0, 0.
Its vector equation is
r→=a2→+μb2→ …(2) Here,a2→=i^+3j^+0k^ b2→=- i^+0j^+0k^
Now,
a2→- a1→=i^+3j^+0k^and b1→×b2→=i^j^k^102-100=0i^-2j^+0k^⇒ b1→×b2→=02+-22+02 =0+4+0 =2and a2→- a1→.b1→×b2→=i^+3j^+0k^.0i^-2j^+0k^ =-6
The shortest distance between the lines r→=a1→+λb1→ and r→=a2→+μb2→ is given by
d=a2→- a1→.b1→×b2→ b1→×b2→ =-62 =3 ∴ d=3 units
Q6.
Answer :
We have
x-12=y-23=z+46x-34=y-36=z+512
Since the first line passes through the point (1, 2, -4) and has direction ratios proportional to 2, 3, 6, its vector equation is
r→=a1→+λb1→ …(1) ⇒r→=i^+2j^-4k^+λ2i^+3j^+6k^
Also, the second line passes through the point (3, 3, -5) and has direction ratios proportional to 4, 6, 12.
Its vector equation is
r→=a2→+μb2→ …(2) ⇒r→=3i^+3j^-5k^+μ4i^+6j^+12k^⇒r→=3i^+3j^-5k^+2μ2i^+3j^+6k^
These two lines pass through the points having position vectors a1→=i^+2j^-4k^ and a2→=3i^+3j^-5k^ and are parallel to the vector b→=2i^+3j^+6k^.
Now,
a2→-a1→=2i^+j^-k^
and
a2→-a1→×b→=2i^+j^-k^×2i^+3j^+6k^ =i^j^k^21-1236 =9i^-14j^+4k^⇒a2→-a1→×b→=92+-142+42 =81+196+16 =293and b→=22+32+62 =4+9+36 =7
The shortest distance between the two lines is given by
a2→-a1→×b→b→=2937units
Q7.
Answer :
(i) r→=i^+2j^+k^+λi^-j^+k^ and r→=2i^-j^-k^+μ2i^+j^+2k^
Comparing the given equations with the equations r→=a1→+λb1→ and r→=a2→+μb2→, we get
a1→=i^+2j^+k^a2→=2i^-j^-k^b1→=i^-j^+k^ b2→=2i^+j^+2k^∴ a2→- a1→=i^-3j^-2k^and b1→×b2→=i^j^k^1-11212 =-3i^+3k^⇒ b1→×b2→=-32+32 =9+9 =32and a2→- a1→.b1→×b2→=i^-3j^-2k^.-3i^+3k^ =-3-6 =-9
The shortest distance between the lines r→=a1→+λb1→ and r→=a2→+μb2→ is given by
d=a2→- a1→.b1→×b2→ b1→×b2→⇒d=-932 =32
(ii) x+17=y+1-6=z+11 and x-31=y-5-2=z-71
Since the first line passes through the point (-1, -1, -1) and has direction ratios proportional to 7, -6, 1, its vector equation is
r→=a1→+λb1→ Here,a1→=-i^-j^-k^ b1→=7i^-6j^+k^
Also, the second line passing through the point (3, 5, 7) has direction ratios proportional to 1,-2, 1.
Its vector equation is
r→=a2→+μb2→ Here,a2→=3i^+5j^+7k^ b2→=i^-2j^+k^
Now,
a2→- a1→=4i^+6j^+8k^and b1→×b2→=i^j^k^7-611-21 =-4i^-6j^-8k^⇒ b1→×b2→=-42+-62+-82 =16+36+64 =116and a2→- a1→.b1→×b2→=4i^+6j^+8k^.-4i^-6j^-8k^ =-16-36-64 =-116
The shortest distance between the lines r→=a1→+λb1→ and r→=a2→+μb2→ is given by
d=a2→- a1→.b1→×b2→ b1→×b2→⇒d=-116116 =116 =229
(iii) r→=i^+2j^+3k^+λi^-3j^+2k^ and r→=4i^+5j^+6k^+μ2i^+3j^+k^
Comparing the given equations with the equations r→=a1→+λb1→ and r→=a2→+μb2→, we get
a1→=i^+2j^+3k^a2→=4i^+5j^+6k^b1→=i^-3j^+2k^ b2→=2i^+3j^+k^∴ a2→- a1→=3i^+3j^+3k^and b1→×b2→=i^j^k^1-32231 =-9i^+3j^+9k^⇒ b1→×b2→=-92+32+92 =81+9+81 =171and a2→- a1→.b1→×b2→=3i^+3j^+3k^.-9i^+3j^+9k^ =-27+9+27 =9
The shortest distance between the lines r→=a1→+λb1→ and r→=a2→+μb2→ is given by
d=a2→- a1→.b1→×b2→ b1→×b2→⇒d=9171 =319
(iv) r→=6i^+2j^+2k^+λi^-2j^+2k^ and r→=-4i^-k^+μ3i^-2j^-2k^
Comparing the given equations with the equations r→=a1→+λb1→ and r→=a2→+μb2→, we get
a1→=6i^+2j^+2k^a2→=-4i^-k^b1→=i^-2j^+2k^ b2→=3i^-2j^-2k^∴ a2→- a1→=-10i^-2j^-3k^and b1→×b2→=i^j^k^1-223-2-2 =8i^+8j^+4k^⇒ b1→×b2→=82+82+42 =64+64+16 =144 =12and a2→- a1→.b1→×b2→=-10i^-2j^-3k^.8i^+8j^+4k^ =-80-16-12 =-108
The shortest distance between the lines r→=a1→+λb1→ and r→=a2→+μb2→ is given by
d=a2→- a1→.b1→×b2→ b1→×b2→⇒d=-10812 =9
Page 28.37 Ex. 28.5
Q8.
Answer :
Given:
r→=i^+2j^-4k^+λ2i^+3j^+6k^ r→=3i^+3j^-5k^+μ2i^+3j^+6k^
These two lines pass through the points having position vectors a1→=i^+2j^-4k^ and a2→=3i^+3j^-5k^ and are parallel to the vector b→=2i^+3j^+6k^.
Now,
a2→-a1→=2i^+j^-k^
and
a2→-a1→×b→=2i^+j^-k^×2i^+3j^+6k^ =i^j^k^21-1236 =9i^-14j^+4k^⇒a2→-a1→×b→=92+-142+42 =81+196+16 =293and b→=22+32+62 =4+9+36 =7
The shortest distance between the two lines is given by
a2→-a1→×b→b→=2937
Page 28.39 (Very Short Answers)
Q1.
Answer :
Since x-axis passes through the the point (0, 0, 0) having position vector a→=0i^+0j^+0k^ and is parallel to the vector b→=1i^+0j^+0k^ having direction ratios proportional to 1, 0, 0, the cartesian equation of x-axis is
x-01=y-00=z-00=x1=y0=z0
Also, its vector equation is
r→=a→+λb→ =0i^+0j^+0k^+λi^+0j^+0k^ =λi^
Q2.
Answer :
Since y-axis passes through the the point (0, 0, 0) having position vector a→=0i^+0j^+0k^ and is parallel to the vector b→=0i^+1j^+0k^ having direction ratios proportional to 0, 1, 0, the cartesian equation of y-axis is
x-00=y-01=z-00=x0=y1=z0
Also, its vector equation is
r→=a→+λb→ =0i^+0j^+0k^+λ0i^+j^+0k^ =λj^
Q3.
Answer :
Since z-axis passes through the the point (0, 0, 0) having position vector a→=0i^+0j^+0k^ and is parallel to the vector b→=0i^+0j^+k^ having direction ratios proportional to 0, 0, 1, the cartesian equation of z-axis is
x-00=y-00=z-01=x0=y0=z1
Also, its vector equation is
r→=a→+λb→ =0i^+0j^+0k^+λ0i^+0j^+k^ =λk^
Q4.
Answer :
The vector equation of the line passing through the point having position vector α→ and parallel to vector β→ is r→=α→+λβ→.
Q5.
Answer :
We have
2x-12=4-y7=z+12
The equation of the line AB can be re-written as
x-121=y-4-7=z+12
The direction ratios of the line parallel to AB are proportional to 1, -7, 2.
Also, the direction cosines of the line parallel to AB are proportional to
112+-72+22, -712+-72+22, 212+-72+22 =154, -754, 254
Q6.
Answer :
We have
6x − 2 = 3y + 1 = 2z − 4
The equation of given line can be re-written as
x-1316=y+1313=z-212⇒x-131=y+132=z-23
The direction ratios of the line parallel to AB are proportional to 1, 2, 3.
Hence, the direction cosines of the line parallel to AB are proportional to
112+22+32, 212+22+32, 312+22+32=114, 214, 314.
Q7.
Answer :
We have
x-22=2y-5-3, z=2
The equation of the given line can be re-written as
x-22=y-52-32= z-20⇒x-24=y-52-3= z-20
The direction ratios of the given line are proportional to 4, -3, 0.
Hence, the direction cosines of the given line are proportional to
442+-32+02, -342+-32+02, 042+-32+02=45, -35, 0
Q8.
Answer :
We have
x-23=y+14=z-10
The given line is parallel to the vector b→=3i^+4j^+0k^.
Let xi^+yj^+zk^ be perpendicular to the given line.
Now,
3x+4y+0z=0
It is satisfied by the coordinates of z-axis, i.e. (0, 0, 1).
Hence, the given line is perpendicular to z-axis.
Q9.
Answer :
We have
x-57=y+2-5=z-21 x-11=y2=z-13
The given lines are parallel to the vectors b1→=7i^-5j^+k^ and b2→=i^+2j^+3k^.
Let θ be the angle between the given lines.
Now,
cos θ=b1→.b2→b1→ b2→ =7i^-5j^+k^.i^+2j^+3k^72+-52+12 12+22+32 =7-10+349+25+1 1+4+9 =0⇒θ=π2
Q10.
Answer :
We have
2x = 3y = −z
The equation of the given line can be re-written as
x12=y13=z-1×3=y2=z-6
The direction ratios of the line parallel to AB are proportional to 3, 2, -6.
Hence, the direction cosines of the line parallel to AB are proportional to
332+22+-62, 232+22+-62, -632+22+-62=37, 27, -67
Q11.
Answer :
We have
2x = 3y = −z
6x = −y = −4z
The given lines can be re-written as
x12=y13=z-1 and x16=y-1=z-14⇒x3=y2=z-6 and x2=y-12=z-3
These lines are parallel to vectors b1→=3i^+2j^-6k^ and b2→=2i^-12j^-3k^.
Let θ be the angle between these lines.
Now,
cos θ=b1→.b2→b1→ b2→=3i^+2j^-6k^.2i^-12j^-3k^32+22+-62 22+-122+-32=6-24+189+4+36 4+144+9=0⇒θ=π2
Q12.
Answer :
We have
x-3-3=y+22λ=z+42 x+13λ=y-21=z+6-5
The given lines are parallel to vectors b1→=-3i^+2λj^+2k^ and b2→=3λi^+j^-5k^.
For b1→⊥b2→, we must have
b1→.b2→=0⇒-3i^+2λj^+2k^.3λi^+j^-5k^=0⇒-7λ-10=0⇒λ=-107
Q13.
Answer :
The shortest distance d between the parallel lines r→=a1→+λb→ and r→=a2→+μb→ is given by
d=a2→-a1→×b→b→
Q14.
Answer :
The shortest distance between the lines r→=a1→+λb1→ and r→=a2→+λb2→ is given by
d=a2→- a1→.b1→×b2→ b1→×b2→
For the lines to be intersecting, d=0.
⇒a2→- a1→.b1→×b2→ b1→×b2→=0⇒a2→- a1→.b1→×b2→=0
Page 28.40 (Very Short Answers)
Q15.
Answer :
We have
2x-13=y+22=z-33
The equation of the line AB can be re-written as
x-1232=y+22=z-33=x-123=y+24=z-36
Thus, the direction ratios of the line parallel to AB are proportional to 3, 4, 6.
Hence, the direction cosines of the line parallel to AB are proportional to
332+42+62, 432+42+62, 632+42+62 = 355, 455, 655
Q16.
Answer :
We have
3-x1=y+2-2=z-54
The equation of the line AB can be re-written as
x-3-1=y+2-2=z-54
Thus, the direction ratios of the line parallel to AB are proportional to -1, -2, 4.
Q17.
Answer :
We have
x-53=y+47=z-62
The given line passes through the point (5, -4, 6) and has direction ratios proportional to 3, 7, 2.
Vector equation of the given line passing through the point having position vector a→=5i^-4j^+6k^ and parallel to a vector b→=3i^+7j^+2k^ is
r→=a→+λb→⇒r→=5i^-4j^+6k^+λ3i^+7j^+2k^
Q18.
Answer :
We have
4-x3=y+33=z+26
The equation of the given line can be re-written as
x-4-3=y+33=z+26
The direction ratios of the line parallel to the given line are proportional to -3, 3, 6.
Hence, the direction cosines of the line parallel to the given line are proportional to
-3-32+32+62, 3-32+32+62, 6-32+32+62 =-16, 16, 26
Q19.
Answer :
The equation of the given line is x+33=4-y5=z+86
It can be re-written as
x+33=y-4-5=z+86
Since the required line is parallel to the given line, the direction ratios of the required line are proportional to 3, -5, 6.
Hence, the cartesian equations of the line passing through the point (-2, 4, -5) and parallel to a vector having direction ratios proportional to 3, -5, 6 is x+23=y-4-5=z+56.
Page 28.40 (Multiple Choice Questions)
Q1.
Answer :
(d) 90°
We have
x+12=y-25=z+34 x-11=y+22=z-3-3
The direction ratios of the given lines are proportional to 2, 5, 4 and 1, 2, -3.
The given lines are parallel to the vectors b1→=2i^+5j^+4k^ and b2→=i^+2j^-3k^.
Let θ be the angle between the given lines.
Now,
cos θ=b1→.b2→b1→ b2→ =2i^+5j^+4k^.i^+2j^-3k^22+52+42 12+22+-32 =2+10-1245 14 =0⇒θ=90°
Q2.
Answer :
(a) coincident
The equation of the given lines are
x1=y2=z3 …(1)
x-1-2=y-2-4=z-3-6=x-11=y-22=z-33 …(2)
Thus, the two lines are parallel to the vector b→=i^+2j^+3k^ and pass through the points (0, 0, 0) and (1, 2, 3).
Now,
a2→-a1→×b→=i^+2j^+3k^×i^+2j^+3k^ =0→ ∵ a→×a→=0→
Since the distance between the two parallel line is 0, the given lines are coincident.
Q3.
Answer :
(a) 4, 5, 7
We have
x-72=y+17-3=z-61 x+51=y+32=z-4-2
The direction ratios of the given lines are proportional to 2, -3, 1 and 1, 2, -2.
The vectors parallel to the given vectors are b1→=2i^-3j^+k^ and b2→=i^+2j^-2k^.
Vector perpendicular to the given two lines is
b→=b1→×b→2 =i^j^k^2-3112-2 =4i^+5j^+7k^
Hence, the direction ratios of the line perpendicular to the given two lines are proportional to 4, 5, 7.
Page 28.41 (Multiple Choice Questions)
Q4.
Answer :
(c) π3
We have
x-11=y-11=z-12 x-1-3-1=y-13-1=z-14
The direction ratios of the given lines are proportional to 1, 1, 2 and -3-1, 3-1, 4.
The given lines are parallel to vectors b1→=i^+j^+2k^ and b2→=-3-1i^+3-1j^+4k^.
Let θ be the angle between the given lines.
Now,
cos θ=b1→.b2→b1→ b2→=i^+j^+2k^.-3-1i^+3-1j^+4k^12+12+12 -3-12+3-12+42=-3-1+3-1+83 24=662=12⇒θ=π3
Q5.
Answer :
(a) 3, 1, −2
We have
x − y + z − 5 = 0 = x − 3y − 6
⇒x-3y-6=0 x-y+z-5=0⇒x=3y+6 … 1 x-y+z-5=0 … 2
From (1) and (2), we get
3y+6-y+z-5=0⇒2y+z+1=0⇒y=-z-12 y=x-63 From 1∴ x-63=y=-z-12
So, the given equation can be re-written as
x-63=y1=z+1-2
Hence, the direction ratios of the given line are proportional to 3, 1,-2.
Q6.
Answer :
(a) 7
We have
x-63=y-72=z-7-2
Let point (1, 2, 3) be P and the point through which the line passes be Q (6, 7, 7). Also, the line is parallel to the vector b→=3i^+2j^-2k^.
Now,
PQ→=5i^+5j^+4k^
∴ b→×PQ→=i^j^k^32-2554 =18i^-22j^+5k^⇒b→×PQ→=182+-222+52 =324+484+25 =833∴ d=b→×PQ→b→ =83317 =49 =7
Q7.
Answer :
(c) r→=a1 1-t i^+a2 1-t j^+a3 1-t k^+t b1 i^+b2 j^+b3 k^
Equation of the line passing through the points having position vectors a1 i^+a2 j^+a3 k^ and b1 i^+b2 j^+b3 k^ is
r→=a1 i^+a2 j^+a3 k^+tb1 i^+b2 j^+b3 k^-a1 i^+a2 j^+a3 k^, where t is a parameter =a1 i^+a2 j^+a3 k^-ta1 i^+a2 j^+a3 k^+tb1 i^+b2 j^+b3 k^ =a11-t i^+a21-t j^+a31-t k^+tb1 i^+b2 j^+b3 k^
Q8.
Answer :
(b) −1
If a line makes angles α, β and γ with the axes, then
cos2α+cos2β+cos2γ=1 …(1)
We have
cos 2α+cos 2β+ cos 2γ=2 cos2α-1+2 cos2β-1+2 cos2γ-1 ∵ cos 2θ=2 cos2θ-1 =2 cos2α+cos2β+cos2γ-3 From 1 =21-3 =-1
Q9.
Answer :
(a) 114, -314, 214
The direction ratios of the line are proportional to 1, -3, 2.
∴ The direction cosines of the line are
112+-32+22, -312+-32+22, 212+-32+22 =114, -314, 214
Q10.
Answer :
(b) π/3
If a line makes angles α, β and γ with the axes, then cos2α+cos2β+cos2γ=1.
Here,
α=π3β=π4
Now,
cos2α+cos2β+cos2γ=1⇒cos2π3+cos2π4+cos2γ=1⇒14+12+cos2γ=1⇒cos2γ=1-34⇒cos2γ=14⇒cos γ=12⇒γ=π3
Q11.
Answer :
(a) 13; 1213, 413, 313
If a line makes angles α, β and γ with the axes, then
cos2α+cos2β+cos2γ=1 …(1)
Let r be the length of the line segment. Then,
r cos α=12, r cos β=4, r cos γ=3 …(2)⇒r cos α2+r cos β2+r cos γ2=122+42+32⇒r2 cos2 α+cos2 β+cos2 γ=169⇒r2 1=169 From 1⇒r=169⇒r=±13⇒r=13 (Since length cannot be negative)
Substituting r = 13 in (2), we get
cos α=1213, cos β=413, cos γ=113
Thus, the direction cosines of the line are 1213, 413, 113.
Q12.
Answer :
(d) coincident
The equations of the given lines are
x1=y2=z3 …(1)
x-1-2=y-2-4=z-3-6⇒x-11=y-22=z-33 …2
Thus, the two lines are parallel to the vector b→=i^+2j^+3k^ and pass through the points (0, 0, 0) and (1, 2, 3).
Now,
a2→-a1→×b→=i^+2j^+3k^×i^+2j^+3k^ =0→ ∵a→×a→=0→
Since, the distance between the two parallel lines is 0, the given two lines are coincident lines.
Q13.
Answer :
(d) perpendicular to z-axis
We have
x-33=y-21=z-10
Also, the given line is parallel to the vector b→=3i^+j^+0k^.
Let xi^+yj^+zk^ be perpendicular to the given line.
Now,
3x+4y+0z=0
It is satisfied by the coordinates of z-axis, i.e. (0, 0, 1).
Hence, the given line is perpendicular to z-axis.
Q14.
Answer :
(d) 330
We have
x-33=y-8-1=z-31 …(1) x+3-3=y+72=z-64 …(2)
We know that line (1) passes through the point (3, 8, 3) and has direction ratios proportional to 3, -1, 1.
Its vector equation is r→=a1→+λb1→, where a1→=3i^+8j^+3k^ and b1→=3i^-j^+k^.
Also, line (2) passes through the point (-3, -7, 6) and has direction ratios proportional to -3, 2, 4.
Its vector equation is r→=a2→+μb2→, where a2→=-3i^-7j^+6k^ and b2→=-3i^+2j^+4k^.
Now,
a2→- a1→=-6i^-15j^+3k^b1→×b2→=i^j^k^3-11-324 =-6i^-15j^+3k^⇒ b1→×b2→=-62+-152+32 =36+225+9 =270a2→- a1→.b1→×b2→=-6i^-15j^+3k^.-6i^-15j^+3k^ =36+225+9 =270
The shortest distance between the lines r→=a1→+λb1→ and r→=a2→+μb2→ is given by
d=a2→- a1→.b1→×b2→ b1→×b2→ =270270 =270 =330
Page 29.4 Ex. 29.1
Q1.
Answer :
(i) The equation of the plane passing through points (2, 1, 0), (3, −2, −2) and (3, 1, 7) is given by
x-2y-1z-03-2-2-1-2-03-21-17-0=0⇒x-2y-1z-01-3-2107=0⇒-21 x-2 – 9 y-1 + 3z = 0⇒-21x + 42 – 9y + 9 + 3z = 0⇒-21x – 9y + 3z + 51 = 0⇒21x + 9y – 3z = 51⇒7x + 3y – z = 17
(ii) The equation of the plane passing through points (−5, 0, −6), (−3, 10, −9) and (−2, 6, −6) is given by
x+5y-0 z+6-3+5 10-0-9+6-2+56-0-6+6 = 0⇒x+5yz+6210-3360 = 0⇒18 x+5 – 9y – 18 z+6 = 0⇒2 x+5 – y – 2 z+6 = 0⇒2x + 10 – y – 2z – 12 = 0⇒2x – y – 2z – 2 = 0
(iii) The equation of the plane passing through points (1, 1, 1), (1, −1, 2) and (−2, −2, 2) is given by
x-1y-1z-11-1-1-12-1-2-1-2-12-1=0⇒x-1y-1z-10-21-3-31=0⇒1 x-1-3 y-1-6 z-1 = 0⇒x – 1 – 3y + 3 – 6z + 6 = 0⇒x – 3y – 6z + 8 = 0
(iv) The equation of the plane passing through points (2, 3, 4), (−3, 5, 1) and (4, −1, 2) is given by
x-2y-3z-4-3-25-31-44-2-1-32-4=0⇒x-2y-3z-4-52-32-4-2=0⇒-16 x – 2 – 16 y – 3 + 16 z – 4 = 0⇒x – 2 + y – 3 – z – 4 = 0⇒x + y – z = 1
(v) The equation of the plane passing through points (0, −1, 0), (3, 3, 0) and (1, 1, 1) is given by
x-0y+1z-03-03+10-01-01+11-0=0⇒x-0y+1z-0340121=0⇒4x – 3 y + 1 + 2z = 0⇒4x – 3y + 2z = 3
Page 29.5 Ex. 29.1
Q2.
Answer :
The equation of the plane passing through the points (0, −1, −1), (4, 5, 1) and (3, 9, 4) is given by
x-0y+1z+14-05+11+13-09+14+1=0⇒xy+1z+14623105=0⇒10x – 14 y + 1 + 22 z + 1 = 0⇒5x – 7 y + 1 + 11 z + 1 = 0⇒5x – 7y + 11z + 4 = 0Substituting the last point (-4, 4, 4) (it means x = -4; y = 4; z = 4) in this plane equation, we get 5 -4 – 7 4 + 11 4 + 4 = 0⇒- 48 + 48 = 0⇒0 = 0So, the plane equation is satisfied by the point (-4, 4, 4).So, the given points are coplanar and the equation of the common plane (as we already found) is5x – 7y + 11z + 4 = 0.
Q3.
Answer :
(i) The equation of the plane passing through points (0, −1, 0), (2, 1, −1), (1, 1, 1) is given by
x-0y+1z-02-01+1-1-01-01+11-0=0⇒xy+1z22-1121=0⇒4x-3 y+1+2 z=0⇒4x-3y+2z-3=0Substituting the last point (3, 3, 0) (it means x = 3; y = 3; z = 0) in this plane equation, we get 4 3-3 3+2 0-3 = 0⇒12-12 = 0⇒0 = 0So, the plane equation is satisfied by the point (3, 3, 0).So, the given points are coplanar.
(ii) The equation of the plane passing through (0, 4, 3), (−1, −5, −3), (−2, −2, 1) is
x-0y-4z-3-1-0-5-4-3-3-2-0-2-41-3=0⇒xy-4z-3-1-9-6-2-6-2=0⇒-18x+10 y-4-12 z-3=0⇒9x-5 y-4+6 z-3=0⇒9x-5y+6z+2=0Substituting the last point (1, 1, -1) (it means x = 1; y = 1; z=-1) in this plane equation, we get 9 1-5 1+6 -1+2=0⇒4-4=0⇒0=0So, the plane equation is satisfied by the point (1, 1, -1).So, the given points are coplanar.
Page 29.6 Ex. 29.2
Q1.
Answer :
We know that the equation of the plane with a, b and c intercepts on the coordianate axes is given by xa+yb+zc=1Given thata = 2; b = -3; c = 4So, the equation of the required plane isx2+y-3+z4 = 1⇒ 6x – 4y + 3z = 12
Page 29.7 Ex. 29.2
Q2.
Answer :
i Equation of the given plane is 4x+3y-6z-12=0⇒4x+3y-6z=12Dividng both sides by 12, we get 4×12 + 3y12 + (-6z)12 = 1212⇒4×12 + 3y12 – 6z12 = 1212⇒x3 + y4 + z-2 = 1 … 1We know that the equation of the plane whose intercepts on the coordianate axes are a, b and c is xa + yb + zc = 1 … 2Comparing (1) and (2), we geta = 3; b = 4; c =-2
ii The equation of the given plane is 2x + 3y – z = 6 Dividng both sides by 6, we get 2×6 + 3y6 – z6 = 66⇒x3 + y2 + z-6 = 1 … 1We know that the equation of the plane whose intercepts on the coordianate axes are a, b and c is xa +yb + zc = 1 … 2Comparing (1) and (2), we geta = 3; b = 2; c =-6
iii Equation of the given plane is2x-y+z=5Dividng both sides by 5, we get2x5+-y5+z5=55⇒x52+y-5+z5=1 … 1We know that the equation of the plane whose intercepts on the coordianate axes are a, b and c isxa+yb+zc=1 … 2Comparing (1) and (2), we geta=52; b=-5; c=5
Q3.
Answer :
Let a, b and c be the intercepts of the given plane on the coordinate axes.Then the plane meets the coordinate axes atA a, 0, 0, B 0, b, 0 and C 0, 0, cGiven that the centroid of the triangle = α, β,γ⇒a+0+03, 0+b+03, 0+0+c3=α, β,γ⇒a3, b3, c3=α, β,γ⇒a3 = α, b3 = β, c3 = γ⇒a=3α, b=3β, c=3γ … 1The equation of the plane whose intercepts on the coordinate axes are a, b and c arexa+yb+zc=1⇒x3α+y3β+z3γ=1 [From (1)]⇒xα+yβ+zγ=3
Q4.
Answer :
We know that the equation of the plane whose intercepts on the coordianate axes are a, b and c isxa+yb+zc=1Given that the plane makes equal intercepts on the coordiante axes.So, a = b = cSo, the equation of the plane isxa+ya+za=1⇒ x + y + z = a … 1This plane passes through the point (2, 4, 6).Substituting this point in (1), we get2 + 4 + 6 = a⇒ a = 12Substituting this in (1), we get x + y + z = 12
Q5.
Answer :
Let a, b and c be the intercepts of the given plane on the coordinate axes.Then the plane meets the coordinate axes atA a, 0, 0, B 0, b, 0 and C 0, 0, cGiven that the centroid of the triangle is 1, -2, 3⇒a+0+03, 0+b+03, 0+0+c3 = 1, -2, 3⇒a3, b3, c3 = 1, -2, 3⇒a3 = 1, b3 = -2, c3 = 3⇒a = 3, b =-6, c = 9 … 1Equation of the plane whose intercepts on the coordinate axes are a, b and c isxa + yb + zc = 1⇒x3 + y-6 + z9 = 1 [From (1)]⇒6x – 3y + 2x = 18
Page 29.12 Ex. 29.3
Q1.
Answer :
We know that the vector equation of the plane passing through a point a→ and normal to n→ isr→. n→=a→. n→Substituting a→ = 2 i^ – j^ + k^ and n→ = 4 i^ + 2 j^ – 3 k^, we get r→. 4 i^ + 2 j^ – 3 k^ = 2 i^ – j^ + k^. 4 i^ + 2 j ^- 3 k^⇒r→. 4 i^ + 2 j^ – 3 k^ = 8 – 2 – 3⇒r→. 4 i^ + 2 j ^- 3 k ^= 3
Q2.
Answer :
i Substituting r→ = x i ^+ y j^ + z k^ in the given equation, we getx i ^+ y j^ + z k^. 12 i^- 3 j^ + 4 k ^ + 5 = 0⇒12x – 3y + 4z + 5 = 0
ii Substituting r→ = x i^ + y j^ + z k^ in the given equation, we getx i ^+ y j^ + z k^ . – i^ + j ^+ 2 k^ = 9⇒-x + y + 2z = 9
Q3.
Answer :
Vector equation of XY-planeThis plane is passing through the origin whose position vector is a →=0 → and perpendicular to z-axis whose position vector is k^.So, the equation of the XY-plane isr→. n→=a→. n→⇒r→. k^=0→. k^⇒r→. k^=0Vector equation of YZ-planeThis plane is passing through the origin whose position vector is a→ =0 → and perpendicular to x-axis whose position vector is i^.So, the equation of the YZ-plane isr→. n→ =a→. n→⇒r→. i^ = 0→. i^⇒r→. i ^= 0Vector equation of XZ-planeThis plane is passing through the origin whose position vector is a→ = 0→ and perpendicular to y-axis whose position vector is j^.So, the equation of the XZ-plane isr→. n→=a→. n→⇒r→. j^=0→. j^⇒r→. j^=0
Q4.
Answer :
i The given equation of plane is2x-y+2z=8⇒xi^+yj^+zk^. 2 i^-j^+2k^=8⇒r→. 2 i^-j^+2k^=8, which is the vector equation of the plane.(Because the vector equation of the plane is r→. n→=a→. n→)
ii The given equation of plane isx+y-z=8⇒xi^+yj^+zk^. i^+j^-k^=8⇒r→. i^+j^-k^=8, which is the vector equation of the plane.(Because the vector equation of the plane is r→. n→=a→. n→)
iii The given equation of plane isx+y=3⇒xi^+yj^+zk^. i^+j^+0k^=3⇒xi^+yj^+zk^. i^+j^=3⇒r→. i^+j^=3, which is the vector equation of the plane.(Because the vector equation of the plane is r→. n→=a→. n→)
Q5.
Answer :
Since the given plane passes through the point (1, -1, 1) and is normal to the line joining A (1, 2, 5) and B (-1, 3, 1), n→ = AB→ = OB→ – OA→ = -i^ + 3j^ + k^ – i^ + 2j^ + 5k^ = -2 i ^+ j^ – 4k^We know that the vector equation of the plane passing through a point a→ and normal to n→ isr→. n→=a→. n→Substituting a→ = i^ – j^ + k^ and n→ = – 2 i^ + j ^- 4 k^, we get r→. -2 i^ + j^ – 4k^ = i^ – j^ + k^ . – 2 i ^+ j ^- 4k^⇒r→. -2 i^ + j^ – 4k^ = -2 – 1 – 4⇒r→. -2 i ^- j^ + 4k^ = -7⇒r→. 2 i ^- j^ + 4k^ = 7For Cartesian form, we need to substitute r→= xi^ + yj^ + zk^ in the vector equation.Then, we getxi^+yj^+zk^. 2 i^-j^+4k^=7⇒2x-y+4z=7
Q6.
Answer :
Let α, β and γ be the angles made by n→ with x, y and z-axes respectively.Given thatα = β = γ⇒cos α = cos β = cos γ⇒l=m=n, where l,m, n are direction cosines of n→.But l2 + m2 + n2 = 1⇒ l2 + l2 + l2 = 1⇒ 3 l2 = 1⇒ l2 = 13⇒ l = 13 (Since α is acute, l = cos α >0)Thus, n→= 3 13i ^+ 13j ^+ 13k^ = i^ + j ^+ k^ (Using r→ = r→ l i^ + m j^ + n k^)We know that the vector equation of the plane passing through a point a→ and normal to n→ isr→. n→ = a→. n→Substituting a→ = 2 i^ + j^ – k^ and n→ = i^ + j^ + k^, we get r→. i^ + j^ + k^ = 2 i^ + j^ – k^. i^ + j^ + k^⇒r→. i^ + j^ + k^ = 2 + 1 – 1⇒r→. i ^+ j^ + k^ = 2For the Cartesian form, we need to substitute r→ = xi ^+ yj ^+ zk^ in the vector equation.Then, we getxi ^+ yj ^+ zk^. i ^+ j^ + k^ = 2⇒x + y + z = 2
Q7.
Answer :
The normal is passing through the points A (0, 0, 0) and B (12, -4, 3). So,n→ = AB→ = OB→ – OA → = 12 i ^- 4 j ^+ 3 k^ – 0 i ^+ 0 j ^+ 0 k^ = 12 i ^- 4 j ^+ 3 k^Since the plane passes through (12, -4, 3), a→ = 12 i^ – 4 j ^+ 3 k^We know that the vector equation of the plane passing through a point a→ and normal to n→ isr→. n→=a→. n→Substituting a→ = i^ – j^ + k^ and n→ = 4 i^ + 2 j^ – 3 k^, we get r→. 12 i^ – 4 j^ + 3 k^ = 12 i^ – 4 j^ + 3 k^. 12 i^ – 4 j ^+ 3 k^⇒r→. 12 i^ – 4 j ^+ 3 k^ = 144 + 16 + 9⇒r→. 12 i ^- 4 j^ + 3 k^ = 169⇒r→. 12 i^ – 4 j ^+ 3 k^ = 169Substituting r→ = xi^ + yj^ + zk^ in the vector equation, we getxi^ + yj ^+ zk^. 12 i ^- 4 j^ + 3 k^ = 169⇒ 12x – 4y + 3z = 169
Q8.
Answer :
We know that the vector equation of the plane passing through a point a→ and normal to n→ isr→. n→=a→. n→Substituting a→ = 2 i^ + 3 j^ + k^ and n→ = 5 i^ + 3 j^ + 2 k^, we get r→. 5 i^ + 3 j^+ 2 k^ = 2 i^ + 3 j^ + k^. 5 i^ + 3 j^+ 2 k^r→. 5 i^ + 3 j^+ 2 k^ = 10 + 9 + 2r→. 5 i^ + 3 j^+ 2 k^ = 21Substituting r→ = xi^ + yj ^+ zk^ in the vector equation, we getxi ^+ yj^ + zk^. 5 i^ + 3 j^ + 2 k^ = 21⇒5x + 3y + 2z = 21
Q9.
Answer :
The normal is passing through the points O (0, 0, 0) and P (2, 3 ,-1). So,n→ = OP→ = 2 i^+3 j^- k^-0 i^+0 j^+0 k^=2 i^+3 j^- k^Since the plane passes through the point (2, 3 ,-1), a→ = 2 i^ + 3 j ^- k^We know that the vector equation of the plane passing through a point a→ and normal to n→ isr→. n→=a→. n→Substituting a→ = 2 i^ + 3 j^ – k^ and n→ = 2 i^ + 3 j^ – k^, we get r→. 2 i^+3 j^- k^=2 i^+3 j^- k^. 2 i^+3 j^- k^⇒r→. 2 i^+3 j^- k^=4+9+1⇒r→. 2 i^+3 j^- k^=14⇒r→. 2 i^+3 j^- k^=14Substituting r→=xi^+yj^+zk^ in the vector equation, we getxi^+yj^+zk^. 2 i^+3 j^- k^=14⇒2x+3y-z=14
Q10.
Answer :
The given equation of the plane is2x + y – 2z = 3Dividng both sides by 3, we get2x3 + y3 + -2z3 = 33⇒x32 + y3 + z-32 = 1 … 1We know that the equation of the plane whose intercepts on the coordianate axes are a, b and c isxa + yb + zc = 1 … 2Comparing (1) and (2), we geta=32; b=3; c=-32Finding the direction cosines of the normalThe given equation of the plane is2x + y – 2z = 8⇒xi^ + yj^ + zk^. 2 i^ + j^ – 2k^ = 8⇒r→. 2 i^ + j^ – 2k^ = 8, which is the vector equation of the plane.(Because the vector equation of the plane is r→. n→=a→. n→,where the normal to the plane, n→=2 i^+j^-2k^.)n→=4+1+4=3So, the unit vector perpendicular to n→ = n→n→=2 i^+j^-2k^3= 23i^+13j^-23k^So, the direction cosines of the normal to the plane are, 23, 13, -23.
Q11.
Answer :
The normal is passing through the points A (0, 0, 0) and B (3, 1, -1). So,n→ = OP→ = 3 i^+ j^- k^-0 i^+0 j^+0 k^ = 3 i^+ j^- k^Since the plane passes through (1, -2, 5), a→ = i^-2 j^+5 k^We know that the vector equation of the plane passing through a point a→ and normal to n→ isr→. n→ = a→. n→Substituting a→ = i^ – j^ + k^ and n→ = 4 i^ + 2 j ^- 3 k^, we get r→. 3 i^ + j^- k^=i^-2 j^+ 5 k^. 3 i^+ j^- k^⇒r→. 3 i^+ j^- k^=3-2-5⇒r→. 3 i^+ j^- k^=-4⇒r→. 3 i^+ j^- k^=-4Substituting r→=xi^+yj^+zk^ in the vector equation, we getxi^ + yj^ + zk^. 3 i^ + j^- k^ = -4⇒3x + y – z = -4
Q12.
Answer :
The normal is passing through the points A (1, 2, 3) and B (3, 4, 5). So,n→ = AB→ = OB→ – OA→ = 3 i^+4 j^+5 k^-i^+2 j^+3 k^ = 2 i^+2 j^+2 k^Mid-point of AB = 1+32, 2+42, 3+52 = 2, 3, 4Since the plane passes through 2, 3, 4, a→ = 2 i^+3 j^+4 k^We know that the vector equation of the plane passing through a point a→ and normal to n→ isr→. n→=a→. n→Substituting a→ = i^ – j^ + k^ and n→ = 4 i^ + 2 j^ – 3 k^, we get r→. 2 i^+2 j^+2 k^ = 2 i^+3 j^+4 k^. 2 i^+2 j^+2 k^⇒r→. 2 i^+2 j^+2 k^ = 4+6+8⇒r→. 2 i^+2 j^+2 k^ = 18⇒r→. 2 i^+j^+k^ = 18⇒r→. i^+j^+k^ = 9Substituting r→ = xi^+yj^+zk^ in the vector equation, we getxi^+yj^+zk^. i^+j^+k^ = 9⇒x+y+z = 9
Q13.
Answer :
i Let n1→ and n2→ be the vectors which are normals to the planes x-y+z=2 and 3x+2y-z=-4 respectively.The given equations of the planes arex – y + z = 2; 3x + 2y – z = -4⇒xi^ + yj^ + zk^. i^ – j^ + k^ = 8; xi^ + yj^ + zk^. 3 i^ + 2 j ^- k^ = -4⇒n1→ = i ^- j^ + k^; n2→ = 3 i^ + 2 j^ – k^Now, n1→. n2→=i^ – j ^+ k^. 3 i^ + 2 j ^- k^ = 3 – 2 – 1 = 0So, the normals to the given planes are perpendicular to each other.
ii Let n1→ and n2→ be the vectors which are normals to the planes r→. 2 i^-j^+3 k^ = 5 and r→. 2 i^-2 j^-2 k^ = 5 respectively.The given equations of the planes arer→. 2 i^-j^+3 k^ = 5 ; r→. 2 i^-2 j^-2 k^ = 5⇒n1→=2 i^-j^+3 k^; n2→=2 i^-2 j^-2 k^Now, n1→. n2→=2 i^-j^+3 k^. 2 i^-2 j^-2 k^=4+2-6=0So, the normals to the given planes are perpendicular to each other.
Q14.
Answer :
The given equation of the plane is2x+2y+2z=8⇒xi^+yj^+zk^. 2 i^+2 j^+2k^=8⇒r→. 2 i^+2 j^+2k^=8, which is the vector equation of the plane.(Because the vector equation of the plane is r→. n→=a→. n→,where the normal to the plane, n→=2 i^+2 j^+2k^.)n→=4+4+4=2 3So, the unit vector perpendicular to n→ = n→n→=2 i^+2 j^+2k^2 3= 13i^+13j^+13k^So, the direction cosines of the normal to the plane are l=13, m=13, n=13Let α, β and γ be the angles made by the given plane with the coordinate axes.Then,l=cos α=13; m=cos β=13; n=cos γ=13⇒cos α=cos β=cos γ⇒α=β=γSo, the given plane is equally inclined to the coordinate axes.
Q15.
Answer :
The given equation of the plane is12x-3y+4z=1⇒xi^+yj^+zk^. 12 i^-3j^+4k^=1⇒r→. 12 i^-3j^+4k^=1, which is the vector equation of the plane.(Because the vector equation of the plane is r→. n→=a→. n→)So, the normal vector, n→=12 i^-3j^+4k^n→=144+9+16=13Unit vector parallel to n→=n→n→=12 i^-3j^+4k^13So, the vector of magnitude 26 units normal to the plane=26 ×12 i^-3j^+4k^13=2 12 i^-3j^+4k^=24 i^-6j^+8k^
Page 29.13 Ex. 29.3
Q16.
Answer :
The normal is passing through the points A (4, -1, 2) and B (-10, 5, 4). So,n→ = AB→ = OB→ – OA→ = -10 i^+5 j^+4 k^-4 i^- j^+2 k^=-14 i^+6 j^+2 k^Since the plane passes through (-10, 5, 4), a→ = -10 i^+5 j^+4 k^We know that the vector equation of the plane passing through a point a→ and normal to n→ isr→. n→=a→. n→Substituting a→ =-10i^+5 j^+4 k^ and n→ =-14 i^+6 j^+2 k^, we get r→. -14 i^+6 j^+2 k^=-10i^+5 j^+4 k^. -14 i^+6 j^+2 k^⇒r→. -14 i^+6 j^+2 k^=140+30+8⇒r→. -2 7 i^-3 j^-k^=178⇒r→. 7 i^-3 j^-k^=-89Substituting r→=xi^+yj^+zk^ in the vector equation, we getxi^+yj^+zk^. 7 i^-3 j^-k^=-89⇒7x-3y-z=-89⇒7x-3y-z+89=0
Q17.
Answer :
The normal is passing through the points A (-1, 2, 3) and B (3, -5, 6). So,n→ = AB→ = OB→ – OA→ = 3 i^-5 j^+6 k^–i^+2 j^+3 k^=4 i^-7 j^+3 k^Mid-point of AB = -1+32, 2-52, 3+62=1, -3 2, 92Since the plane passes through 1, -3 2, 92, a→ = i^-32 j^+92 k^We know that the vector equation of the plane passing through a point a→ and normal to n→ isr→. n→=a→. n→Substituting a→ = i^ – j^ + k^ and n→ = 4 i^-7 j^+3 k^, we get r→. 4 i^-7 j^+3 k^ = i^-32 j^+92 k^. 4 i^-7 j^+3 k^⇒r→. 4 i^-7 j^+3 k^=28Substituting r→=xi^+yj^+zk^ in the vector equation, we getxi^+yj^+zk^. 4 i^-7 j^+3 k^ = 28⇒4x-7y+3z = 28⇒4x-7y+3x-28 = 0
Q18.
Answer :
We know that the vector equation of the plane passing through a point a→ and normal to n→ isr→. n→=a→. n→Substituting a→ = 5 i^ +2 j^ -4 k^ and n→ = 2 i^ +3 j^- k^ (because the direction ratios of n→ are 2, 3, -1), we getr→. 2 i^ +3 j^- k^= 5 i^ +2 j^ -4 k^. 2 i^ +3 j^- k^⇒r→. 2 i^ +3 j^- k^=10+6+4⇒r→. 2 i^ +3 j^- k^=20For Cartesian form, we need to substitute r→ = x i^+y j^+z k^ in this equation. Then, we getx i^+y j^+z k^. 2 i^ +3 j^- k^=20⇒2x+3y-z=20
Q19.
Answer :
The normal is passing through the points O (0, 0, 0) and P (1, 2, -3). So,n→ = OP→ = i^+2 j^-3 k^-0 i^+0 j^+0 k^=i^+2 j^-3 k^Since the plane passes through P (1, 2, -3), a→ = i^+2 j^-3 k^We know that the vector equation of the plane passing through a point a→ and normal to n→ isr→. n→=a→. n→Substituting a→ = 2 i^+3 j^- k^ and n→ = i^+2 j^-3 k^ in the relation, we get r→. i^+2 j^-3 k^=i^+2 j^-3 k^. i^+2 j^-3 k^⇒r→. i^+2 j^-3 k^=1+4+9⇒r→. i^+2 j^-3 k^=14⇒r→. i^+2 j^-3 k^=14Substituting r→=xi^+yj^+zk^ in the vector equation, we getxi^+yj^+zk^. i^+2 j^-3 k^=14⇒x+2y-3z=14
Page 29.18 Ex. 29.4
Q1.
Answer :
Given thatnormal vector, n→=i^Now, n^=n→n→=k^k^=k^1=k^The equation of a plane in normal form isr→. n^=d (where d is the distance of the plane from the origin)Substituting n^=k^ and d = 3 in the relation, we get r→. k^=3
Q2.
Answer :
It is given that the normal vector, n→=i^-2 j^-2 k^Now, n^=n→n→=i^-2 j^-2 k^1+4+4=i^-2 j^-2 k^3=13 i^-23 j^-23k^The equation of a plane in normal form isr→. n^=d (where d is the distance of the plane from the origin)Substituting n^=13 i^-23 j^-23k^ and d = 5Here,r→. 13 i^-23 j^-23k^=5
Q3.
Answer :
The given equation of the plane is2x – 3y – 6z = 14 … 1Now, 22+-32+-62 = 4+9+36 = 49 = 7Dividing (1) by 7, we get27x – 37y – 67z = 2 … 2The Cartesian equation of the normal form of a plane islx+ my + nz = p… 3,where l, m and n are direction cosines of normal to the plane and p is the length of the perpendicular from the origin to the plane.Comparing (1) and (2), we getdirection cosines: l=27, m=-37, n=-6 7 andlength of the perpendicular from the origin to the plane: p=2
Q4.
Answer :
The given equation of the plane isr→. i^-2 j^+2 k^+6 = 0⇒r→. i^-2 j^+2 k^ =-6 or r→. n→ = -6, where n→ = i^-2 j^+2 k^n→ =1+4+4 = 3For reducing the given equation to normal form, we need to divide it by n→. Then, we getr→. n→n→ = -6n→⇒r→. i^-2 j^+2 k^3 = -63⇒r→. 13 i^-23 j^+23k^ = -2Dividing both sides by -1, we getr→. -13 i^+23 j^-23k^ = 2 … 1The equation of the plane in normal form isr→. n ^= d … 2(where d is the distance of the plane from the origin)Comparing (1) and (2), length of the perpendicular from the origin to the plane = d = 2 units
Q5.
Answer :
The given equation of the plane is2x-3y+6z+14 = 02x-3y+6z =-14 … 1Now, 22 + -32 + 62 = 4 + 9 + 36 = 49 = 7Dividing (1) by 7, we get27x – 37y + 67z = -2 Multiplying both sides by -1, we get-27x+37y-67z=2This is the normal form of the given equation of the plane.
Q6.
Answer :
It is given that the direction ratios of the normal vector n→ are 12, -3, 4.So, n→=12 i^-3 j^+4 k^n→=122+-32+42=144+9+16=169=13Now, n^=n→n→=12 i^-3 j^+4 k^13=1213 i^-313 j^+413 k^Length of the perpendicular from the origin to the plane, d = 5Equation of the plane in normal form isr→. n^=d⇒r→. 1213 i^-313 j^+413 k^=5
Q7.
Answer :
The given equation of the plane isx+2y+3z-6=0x+2y+3z=6 ⇒r→. i^ + 2 j ^+ 3 k^ = 6 or r→. n→ = 6,where n→ = i^+2 j^+3 k^… 1Now, n→ = 12 + 22 + 32=1 + 4 + 9 = 14Unit vector to the plane, n⏜ = n→n→ = i ^+ 2 j^ + 3 k^14= 114i^ + 214j^ +314k^
Q8.
Answer :
Let α, β and γ be the angles made by n→ with x, y and z-axes, respectively.It is given thatα=β=γ⇒cos α=cos β=cos γ⇒l=m=n, where l,m, n are direction cosines of n→.But l2+m2+n2=1⇒l2+l2+l2=1⇒3 l2=1⇒l2=13⇒l=13So, l=m=n=13It is given that the length of the perpendicular of the plane from the origin, p = 3 3The normal form of the plane is lx+my+nz=p⇒13x + 13y +13z = 33⇒x + y + z = 33 3 ⇒x + y + z = 9
Q9.
Answer :
The normal is passing through the points A (1, 4, 2) and B (2, 3, 5).So, n→ = AB→ = OB→ – OA→ = 2 i^+3 j^+5 k^-i^+4 j^+2 k^= i^-j^+3 k^We know that the vector equation of the plane passing through a point (1, 2, 1) (a→) and normal to n→ isr→. n→=a→. n→Substituting a→ = i^ +2 j^ + k^ and n→ = i^-j^+3 k^, we get r→. i^-j^+3 k^= i^ +2 j^ + k^. i^-j^+3 k^⇒r→. i^-j^+3 k^=1-2+3⇒r→. i^-j^+3 k^=2 … 1To find the perpendicular distance of this plane from the origin, we have to reduce this to normal form.We have n→=i^-j^+3 k^; n→=1+1+9=11Dividing (1) by 11, we getr→. 111i^-111j^+311 k^ = 211, which is the normal form of plane (1).So, the perpendicular distance of plane (1) from the origin = 211
Q10.
Answer :
Given, normal vector, n→=2 i^-3 j^+4 k^Now, n^=n→n→=2 i^-3 j^+4 k^4+9+16=2 i^-3 j^+4 k^29=229 i^-329 j^+429k^The equation of the plane in normal form isr→. n^=d (where d is the distance of the plane from the origin)Substituting, n^=229 i^-329 j^+429k^ and d = 629 here, we get r→. 229 i^-329 j^+429k^=629… (1)Cartesian formFor Cartesian form, substituting r→= x i^+y j^+z k^ in (1), we getx i^+y j^+z k^ . 229 i^-329 j^+429k^= 629⇒2x-3y+4z29=629⇒2x-3y+4z=6
Q11.
Answer :
The given equation of the plane is2x-3y+4z=6 … 1Now, 22 + -32 + 42 = 4+9+16 = 29 Dividing (1) by 29, we get229x-329y+429z = 629, which is the normal form of plane (1).So, the length of the perpendicular from the origin to the plane=629
Page 29.21 Ex. 29.5
Q1.
Answer :
Let A (1, 1, 1), B (1, -1, 1) and C (-7, -3, -5) be the coordinates.The required plane passes through the point A (1, 1, 1) whose position vector is a→ = i^ + j^ + k^ and is normal to the vector n→ given byn →= AB →× AC .→Clearly, AB→ = OB→ – OA →= i ^- j^ + k^ – i ^+ j ^+ k^ = 0 i^ – 2 j^ + 0 k^AC →= OC→ – OA →=-7 i^ – 3 j^ – 5 k^ – i ^+ j^ + k^ = -8 i^ -4 j^ -6 k^n →= AB→ × AC →=i^j^k^0-20-8-4-6 = 12 i^ + 0 j^ -16 k^The vector equation of the required plane isr→. n→ = a→. n→⇒r→. 12 i^ + 0 j^ -16 k^ = i^ + j^ + k^. 12 i^ + 0 j^ -16 k^⇒r→. 4 3 i^ – 4 k^ = 12 + 0 – 16⇒r→. 4 3 i^ – 4 k^ = -4⇒r→. 3 i^ – 4 k^ = -1⇒r→. 3 i ^- 4 k^ + 1 = 0
Q2.
Answer :
The required plane passes through the point P (2, 5, -3) whose position vector is a→=2 i^+5 j^-3 k^ and is normal to the vector n→ given byn →= PQ→×PR.→Clearly, PQ →= OQ →- OP →= -2 i^ – 3 j^ + 5 k^ – 2 i^ + 5 j^ – 3 k^ = -4 i ^- 8 j^ + 8 k^PR →= OR →- OP →= 5 i^ + 3 j^ – 3 k^ – 2 i^ + 5 j ^- 3 k^ = 3 i ^- 2 j^ – 0 k^n→ = PQ→ × PR →= i^j^k^-4-883-20 = 16 i^ + 24 j^ + 32 k^The vector equation of the required plane isr→. n→ = a→. n→⇒r→. 16 i^+24 j^+32 k^ = 2 i^+5 j^-3 k^. 16 i^+24 j^+32 k^⇒r→. 8 2 i^+3 j^+4 k^ = 32+120-96⇒r→. 8 2 i^+3 j^+4 k^ = 56⇒r→. 2 i^+3 j^+4 k^ = 7
Q3.
Answer :
The required plane passes through the point A (a, 0, 0) whose position vector is a→=a i^ + 0 j ^+ 0 k^ and is normal to the vector n→ given byn→=AB→ × AC→.Clearly, AB→ = OB →- OA→ = 0 i ^+ b j^ + 0 k^ – a i^ + 0 j^ + 0 k^ = -a i ^+ b j^ + 0 k^AC →= OC→ – OA →= 0 i^ + 0 j^ + c k^ – a i ^+ 0 j^ + 0 k^ = -a i^ + 0 j^ + c k^n →= AB →× AC→ = i^j^k^-a b 0-a0c = bc i^ + ac j^ + ab k^The vector equation of the required plane isr→. n→ = a→. n→⇒r→. bc i^ + ac j^ + ab k^ = a i^ + 0 j^ + 0 k^. bc i^ + ac j^ +ab k^⇒r→. bc i^ + ac j^ + ab k^ = abc + 0 + 0⇒r→. bc i^ + ac j^ + ab k^ = abc … 1Now, n→ = bc2 + ac2 + ab2 = b2c2 + a2c2 + a2b2For reducing (1) to normal form, we need to divide both sides of (1) by b2c2+a2c2+a2b2. Then, we getr→. bc i^+ac j^ +ab k^b2c2+a2c2+a2b2 = abc b2c2+a2c2+a2b2, which is the normal form of plane (1).So, the distance of plane (1) from the origin,p = abc b2c2 + a2c2 + a2b2,⇒1p = b2c2 + a2c2 + a2b2abc⇒1p2 = b2c2 + a2c2 + a2b2a2b2c2⇒1p2 = 1a2 + 1b2 + 1c2
Q4.
Answer :
Let A (1, 1, -1), B (6, 4, -5) and C (-4, -2, 3).The required plane passes through the point A (1, 1, -1) whose position vector is a→ = i ^+ j ^- k^ and is normal to the vector n→ given byn→=AB →× AC→Clearly, AB→ = OB →- OA →= 6 i^ + 4 j^ – 5 k^ – i^ + j ^- k^ = 5 i^ + 3 j^ – 4 k^AC →= OC→ – OA→ = -4 i^ – 2 j^ + 3 k^ – i^ + j ^- k^ = -5 i^ – 3 j^ + 4 k^n→=AB→ × AC→ = i^j^k^53-4-5-34 = 0 i^ + 0 j^ +0 k^ = 0→So, the given points are collinear.Thus, there will be infinite number of planes passing through these points.Their equations (passing through (1, 1, -1) are given bya x – 1 + b y – 1 + c z + 1 = 0 … 1Since this passes through B (6, 4, -5),a 6 – 1 + b 4 – 1 + c -5 + 1 = 0⇒5a + 3b – 4c = 0 … 2From (1) and (2), the equations of the infinite planes area x – 1 + b y – 1 + c z + 1 = 0, where 5a + 3b – 4c = 0.
Q5.
Answer :
Let A (3, 4, 2), B (2, -2, -1) and C (7, 0, 6) be the points represented by the given position vectors.The required plane passes through the point A (3, 4, 2) whose position vector is a→=3 i^+4 j^+2 k^ and is normal to the vector n→ given byn→=AB→×AC→.Clearly, AB→=OB→-OA→=2 i^-2 j^-k^-3 i^+4 j^+2 k^=- i^-6 j^-3 k^AC→=OC→-OA→=7 i^+0 j^+6 k^-3 i^+4 j^+2 k^=4 i^-4 j^+4 k^n→=AB→×AC→=i^j^k^-1-6-34-44=-36 i^-8 j^ +28 k^The vector equation of the required plane isr→. n→=a→. n→⇒r→. -36 i^-8 j^ +28 k^=3 i^+4 j^+2 k^. -36 i^-8 j^ +28 k^⇒r→. -4 9 i^+2 j^+7 k^=-108-32+56⇒r→. -4 9 i^+2 j^+7 k^=-84⇒r→. 9 i^+2 j^+7 k^=21
Page 29.27 Ex. 29.6
Q1.
Answer :
i) We know that the angle between the planes r→.n1→ = d1, r→. n2→=d2 is given bycos θ=n1→. n2→n1→ n2→Here, n1→=2 i^-3 j^+4 k^; n2→=- i^+j^+0 k^So, cos θ=2 i^-3 j^+4 k^. – i^+j^+0 k^2 i^-3 j^+4 k^ – i^+j^+0 k^ = -2-34+9+16 1+1+0 = -529 2 = -558⇒θ=cos-1-558
ii) We know that the angle between the planes r→.n1→ = d1, r→. n2→=d2 is given bycos θ=n1→. n2→n1→ n2→Here, n1→=2 i^- j^+2 k^; n2→=3 i^+6 j^-2 k^So, cos θ=2 i^- j^+2 k^. 3 i^+6 j^-2 k^2 i^- j^+2 k^ 3 i^+6 j^-2 k^=6-6-44+1+4 9+36+4=-43 7=-421⇒θ=cos-1-421
iii) We know that the angle between the planes r→.n1→ = d1, r→. n2→=d2 is given bycos θ=n1→. n2→n1→ n2→Here, n1→=2 i^ +3 j^-6 k^; n2→= i^-2 j^+2 k^So, cos θ=2 i^ +3 j^-6 k^. i^-2 j^+2 k^2 i^ +3 j^-6 k^ i^-2 j^+2 k^=2-6-124+9+36 1+4+4=-167 3=-1621⇒θ=cos-1-1621
Q2.
Answer :
i) We know that the angle between the planes a1x + b1y + c1z + d1 = 0 and a2x + b2y + c2z + d2 = 0 is given bycos θ=a1a2+b1b2+c1c2a12+b12+c12 a22+b22+c22So, the angle between 2x – y + z = 4 and x + y + 2z = 3 is given by cos θ=2 1 + -1 1 + 1 222 + -12 + 12 12 + 12 + 22=2 – 1 + 24 + 1 + 1 1 + 1 + 4=36 6=36=12⇒θ = cos-112 = π3
ii) We know that the angle between the planes a1x+b1y+c1z+d1=0 and a2x+b2y+c2z+d2=0 is given bycos θ=a1a2+b1b2+c1c2a12+b12+c12 a22+b22+c22So, the angle between x+y-2z=3 and 2x-2y+z=5 is given by cos θ=1 2+1 -2+-2 112+12+-22 22+-22+12=2-2-21+1+4 4+4+1=-26 9=-236⇒θ=cos-1-236
iii) We know that the angle between the planes a1x+b1y+c1z+d1=0 and a2x+b2y+c2z+d2=0 is given bycos θ=a1a2+b1b2+c1c2a12+b12+c12 a22+b22+c22So, the angle between x-y+z=5 and x+2y+z=9 is given by cos θ=1 1+-1 2+1 112+-12+12 12+22+12=1-2+11+1+1 1+4+1=03 6=0⇒θ=cos-10=π2
iv) We know that the angle between the planes a1x+b1y+c1z+d1=0 and a2x+b2y+c2z+d2=0 is given bycos θ=a1a2+b1b2+c1c2a12+b12+c12 a22+b22+c22So, the angle between 2x-3y+4z=1 and -x+y+0z=4 is given by cos θ=2 -1+-3 1+4 022+-32+42 -12+12+02=-2-3+04+9+16 1+1+0=-529 2=-558⇒θ=cos-1-558
v) We know that the angle between the planes a1x+b1y+c1z+d1=0 and a2x+b2y+c2z+d2=0 is given bycos θ=a1a2+b1b2+c1c2a12+b12+c12 a22+b22+c22So, the angle between 2x+y-2z=5 and 3x-6y-2z=7 is given by cos θ=2 3+1 -6+-2 -222+12+-22 32+-62+-22=6-6+44+1+4 9+36+4=43 7=421⇒θ=cos-1421
Page 29.28 Ex. 29.6
Q3.
Answer :
i) We know that the planes r→.n1→ = d1, r→. n2→=d2 are perpendicular to each other only if n1→. n2→=0.Here, n1→=2 i^- j^+ k^; n2→=- i^-j^+k^Now, n1→. n2→ = 2 i^- j^+ k^. – i^-j^+k^=-2 + 1 + 1 = 0So,the given planes are perpendicular.
ii) We know that the planes a1x+b1y+c1z+d1=0 and a2x+b2y+c2z+d2=0 are perperndicular to each other only if a1a2+b1b2+c1c2=0.The given planes are x-2y+4z=10 and 18x+17y+4z=49.⇒a1=1; b1=-2; c1=4; a2=18; b2=17; c2=4Now, a1a2+b1b2+c1c2=1 18+-2 17+4 4=18-34+16=0So, the given planes are perpendicular.
Q4.
Answer :
i) We know that the planes r→.n1→ = d1, r→. n2→=d2 are perpendicular to each other only if n1→. n2→=0.Here, n1→= i^ + 2 j ^+ 3 k^; n2→ = λ i^ + 2 j ^- 7 k^The given planes are perpendicular.⇒n1→. n2→ = 0⇒i^+2 j^+3 k^. λ i^+2 j^-7 k^ = 0⇒λ+4-21=0⇒λ-17=0⇒λ=17
ii) We know that the planes a1x+b1y+c1z+d1=0 and a2x+b2y+c2z+d2=0 are perperndicular to each other only if a1a2+b1b2+c1c2=0The given planes are 2x-4y+3z=5 and x+2y+λz=5.⇒a1=2; b1=-4; c1=3; a2=1; b2=2; c2=λIt is given that the given planes are perpendicular. ⇒a1a2+b1b2+c1c2=0⇒2 1+-4 2+3 λ=0⇒2-8+3λ=0⇒3λ=6⇒λ=2
iii) We know that the planes a1x+b1y+c1z+d1=0 and a2x+b2y+c2z+d2=0 are perperndicular to each other only if a1a2+b1b2+c1c2=0The given planes are 3x-6y-2z=7 and 2x+y-λz=5.⇒a1=3; b1=-6; c1=-2; a2=2; b2=1; c2=-λThe given planes are perpendicular. ⇒a1a2+b1b2+c1c2=0⇒3 2+-6 1+-2 -λ=0⇒6-6+2λ=0⇒2λ=0⇒λ=0
Q5.
Answer :
The equation of any plane passing through (-1, -1, 2) isa x+1+b y+1+c z-2=0 … 1It is given that (1) is perpendicular to each of the planes 3x+2y-3z=1 and 5x-4y+z=5. Then,3a+2b-3c=0 … 25a-4b+c=0 … 3Solving (1), (2) and (3), we getx+1y+1z-232-35-41 = 0⇒-10 x + 1 – 18 y + 1 -22 z – 2 = 0⇒5 x + 1 + 9 y + 1 + 11 z – 2 = 0⇒5x + 5 + 9y + 9 + 11z – 22 = 0⇒5x + 9y + 11z – 8 = 0
Q6.
Answer :
The equation of any plane passing through (1, -3, -2) isa x-1+b y+3+c z+2=0 … 1It is given that (1) is perpendicular to the planes x+2y+2z=5 and 3x+3y+2z=8. Then,a+2b+2c=0 … 23a+3b+2c=0 … 3Solving (1), (2) and (3), we getx-1y+3z+2122332=0⇒-2 x-1+4 y+3-3 z+2=0⇒-2x+2+4y+12-3z-6=0⇒2x-4y+3z-8=0
Q7.
Answer :
The equation of any plane passing through the origin (0, 0, 0) isa x-0+b y-0+c z-0=0 ax+by+cz=0… 1It is given that (1) is perpendicular to the planes x+2y-z=1 and 3x-4y+z=5. Then,a+2b-c=0 … 23a-4b+c=0 … 3Solving (1), (2) and (3), we getxyz12-13-41=0⇒-2x-4y-10z=0⇒x+2y+5z=0
Q8.
Answer :
The equation of any plane passing through (1, -1, 2) isa x-1+b y+1+c z-2=0 … 1It is given that (1) is passing through (2, -2, 2). So,a 2-1+b -2+1+c 2-2=0 ⇒a-b+0c=0… 2It is given that (1) is perpendicular to the plane 6x-2y+2z=9. So,6a-2b+2c=0⇒3a-b+c=0… 3Solving (1), (2) and (3), we getx-1y+1z-21-103-11=0⇒-1 x-1-1 y+1+2 z-2=0⇒-x+1-y-1+2z-4=0⇒x+y-2z+4=0
Q9.
Answer :
The equation of any plane passing through (2, 2, 1) isa x-2+b y-2+c z-1=0 … 1It is given that (1) is passing through (9, 3, 6). So,a 9-2+b 3-2+c 6-1=0⇒7a+b+5c=0… 2It is given that (1) is perpendicular to the plane 2x+6y+6z=1. So,2a+6b+6c=0⇒a+3b+3c=0… 3Solving (1), (2) and (3), we getx-2y-2z-1715133=0⇒-12 x-2-16 y-2+20 z-1=0⇒3 x-2+4 y-2 -5 z-1=0⇒3x+4y-5z=9
Q10.
Answer :
The equation of any plane passing through (-1, 1, 1) isa x+1+b y-1+c z-1=0 … 1It is given that (1) is passing through (1, -1, 1). So,a 1+1+b -1-1+c 1-1=0 ⇒2a-2b+0c=0… 2It is given that (1) is perpendicular to the plane x+2y+2z=5. So,a+2b+2c=0 … 3Solving (1), (2) and (3), we getx+1y-1z-12-20122=0⇒-4 x+1-4 y-1+6 z-1=0⇒2 x+1+2 y-1-3 z-1=0⇒2x+2y-3z+3=0
Q11.
Answer :
The equation of the plane parallel to the plane ZOX is y=b … 1, where b is a constant.It is given that this plane passes through (0, 3, 0). So,3=bSubstituting this value in (1), we get y=3, which is the required equation of the plane.
Q12.
Answer :
The equation of any plane passing through (1, -1, 2) isa x-1+b y+1+c z-2=0 … 1It is given that (1) is perpendicular to the plane 2x+3y-2z=5. So,2a+3b-2c=0… 2It is given that (1) is perpendicular to the plane x+2y-3z=8. So,a+2b-3c=0 … 3Solving (1), (2) and (3), we getx-1y+1z-223-212-3=0⇒-5 x-1+4 y+1+1 z-2=0⇒5x-4y-z=7
Q13.
Answer :
Substituting r→=x i^+y j^+z k^ in the given equation of the plane, we getx i^+y j^+z k^. i^+j^+k^=2⇒x+y+z-2=0 … (1)The equation of a plane which is parallel to plane (1) is of the formx+y+z=k… 2It is given that plane (2) is passing through the point a, b, c. So,a+b+c=kSubstituting this value of k in (2), we get x+y+z=a+b+c, which is the required equation of the plane.
Q14.
Answer :
The equation of any plane passing through point (-1, 3, 2) isa x+1+b y-3+c z-2=0 … 1It is given that (1) is perpendicular to the plane x+2y+3z=5. So,a+2b+3c=0 … 2It is given that (1) is perpendicular to the plane 3x+3y+z=0. So,3a+3b+c=0 … 3Solving (1), (2) and (3), we getx+1y-3z-2123331=0⇒-7 x+1+8 y-3-3 z-2=0⇒7x-8y+3z+25=0
Q15.
Answer :
The equation of any plane passing through (2, 1, -1) isa x-2+b y-1+c z+1=0 … 1It is given that (1) is passing through (-1, 3, 4). So,a -1-2+b 3-1+c 4+1=0⇒-3a+2b+5c… 2It is given that (1) is perpendicular to the plane x-2y+4z=10. So,a-2b+4c=0… 3Solving (1), (2) and (3), we getx-2y-1z+1-3251-24=0⇒18 x-2+17 y-1+4 z+1=0⇒18x+17y+4z-49=0
Page 29.31 Ex. 29.7
Q1.
Answer :
i) We know that the equation r→=a→+λb→+μc→ represents a plane passing through a point whose position vector is a→ and parallel to the vectors b→ and c→.Here, a→=2 i^+0 j^-k^; b→=i^; c→=i^-2 j^-k^Normal vector, n→=b→×c→=i^j^k^1001-2-1=0 i^+j^-2 k^=j^-2 k^The vector equation of the plane in scalar product form isr→. n→=a→. n→⇒r→. j^-2 k^=2 i^+0 j^-k^. j^-2 k^⇒r→. j^-2 k^=2
ii) The given equation of the plane isr→=1+s-t i^+2-s j^+3-2s+2t k^⇒r→=i^+2 j^+3 k^+s i^-j-2 k^+t – i^+0 j^+2 k^ We know that the equation r→=a→+sb→+t c→ represents a plane passing through a point whose position vector is a→ and parallel to the vectors b→ and c→.Here, a→=i^+2 j^+3 k^; b→=i^-j-2 k^; c→=- i^+0 j^+2 k^Normal vector, n→=b→×c→=i^j^k^1-1-2-102=-2 i^+0 j^-k^=-2 i^- k^The vector equation of the plane in scalar product form isr→. n→=a→. n→⇒r→. -2 i^- k^=i^+2 j^+3 k^. -2 i^- k^⇒r→. -1 2 i^+k^=-2+0-3⇒r→. -1 2 i^+k^=-5⇒r→. 2 i^+k^=5
iii) We know that the equation r→=a→+λb→+μc→ represents a plane passing through a point whose position vector is a→ and parallel to the vectors b→ and c→.Here, a→=i^+ j^+0 k^; b→=i^+2 j^-k^; c→=-i^+ j^-2 k^Normal vector, n→=b→×c→=i^j^k^12-1-11-2=-3 i^+3 j^+3 k^The vector equation of the plane in scalar product form isr→. n→=a→. n→⇒r→. -3 i^+3 j^+3 k^=i^+ j^+0 k^. -3 i^+3 j^+3 k^⇒r→. -3 i^+3 j^+3 k^=-3+3⇒r→. 3 -i^+ j^+k^=0⇒r→. -i^+ j^+k^=0
iv) We know that the equation r→=a→+λb→+μc→ represents a plane passing through a point whose position vector is a→ and parallel to the vectors b→ and c→.Here, a→=i^- j^+0 k^; b→=i^+j^+k^; c→=4 i⏜-2 j^+3 k^Normal vector, n→=b→×c→=i^j^k^1114-23=5 i^+j^-6 k^The vector equation of the plane in scalar product form isr→. n→=a→. n→⇒r→. 5 i^+j^-6 k^=i^- j^+0 k^. 5 i^+j^-6 k^⇒r→. 5 i^+j^-6 k^=5-1+0⇒r→. 5 i^+j^-6 k^=4⇒r→. 5 i^+j^-6 k^=4
Page 29.32 Ex. 29.7
Q2.
Answer :
i r→=i^- j^+ 0 k^+s -i^ + j + 2 k^ + t i^ + 2 j^ + k^ We know that the equation r→=a→ + sb→ + t c→ represents a plane passing through a point whose position vector is a→ and parallel to the vectors b→ and c→.Here, a→=i^ – j^ + 0 k^; b→=-i^ + j + 2 k^; c→ = i^ + 2 j^ + k^Normal vector, n→=b→×c→=i^j^k^-112121=-3 i^ + 3 j^ – 3 k^The vector equation of the plane in scalar product form isr→. n→=a→. n→⇒r→. -3 i^ + 3 j^ – 3 k^ = i^ – j ^+ 0 k^. -3 i ^+ 3 j^ – 3 k^⇒r→. -3 i^ – j ^+ k^ =-3 – 3 + 0⇒r→. -3 i^ – j^ + k^ = -6⇒r→. i^ – j^ + k^ = 2For Cartesian form, let us substitute r→ = x i^ + y j^ + z k^ here. Then, we getx i^ + y j^ + z k^. i^ – j ^+ k^ = 2⇒x – y + z = 2
ii The given equation of the plane isr→=1+s+t i^+2-s+t j^+3-2s+2t k^⇒r→=i^+2 j^+3 k^+s i^-j-2 k^+t i^+j^+2 k^ We know that the equation r→=a→+sb→+t c→ represents a plane passing through a point whose position vector is a→ and parallel to the vectors b→ and c→.Here, a→=i^+2 j^+3 k^; b→=i^-j-2 k^; c→=i^+j^+2 k^Normal vector, n→=b→×c→=i^j^k^1-1-2112= 0 i^-4 j^+2 k^=-4 j^+2 k^The vector equation of the plane in scalar product form isr→. n→=a→. n→⇒r→. -4 j^+2 k^=i^+2 j^+3 k^. -4 j^+2 k^⇒r→. -2 2 j^-k^=0-8+6⇒r→. -2 2 j^-k^=-2⇒r→. 2 j^-k^=1For Cartesian form, let us substitute r→=x i^+y j^+z k^ here. Then, we getx i^+y j^+z k^. 2 j^-k^=1⇒2y-z=1
Q3.
Answer :
i The given equation of the plane isr→=λ-2μ i^+3-μ j^+2λ+μ k^⇒r→=0 i^+3 j^+0 k^+λ i^+0 j^+2 k^+μ -2 i^-j^+k^We know that the equation r→=a→+λb→+μc→ represents a plane passing through a point whose position vector is a→ and parallel to the vectors b→ and c→.Here, a→=0 i^+3 j^+0 k^; b→=i^+0 j^+2 k^; c→=-2 i^-j^+k^Normal vector, n→=b→×c→=i^j^k^102-2-11=2 i^-5 j^-k^The vector equation of the plane in scalar product form isr→. n→=a→. n→⇒r→. 2 i^-5 j^-k^ = 0 i^+3 j^+0 k^. 2 i^-5 j^-k^⇒r→. 2 i^-5 j^-k^ = 0 – 15 + 0⇒r→. 2 i^-5 j^-k^ + 15 = 0
ii We know that the equation r→=a→+λb→+μc→ represents a plane passing through a point whose position vector is a→ and parallel to the vectors b→ and c→.Here, a→=2 i^+2 j^- k^; b→=i^+2 j^+3 k^; c→=5 i-2 j^+7 k^Normal vector, n→=b→×c→=i^j^k^1235-27=20 i^+8 j^-12 k^The vector equation of the plane in scalar product form isr→. n→=a→. n→⇒r→. 20 i^+8 j^-12 k^=2 i^+2 j^- k^. 20 i^+8 j^-12 k^⇒r→. 4 5 i^+2 j^-3 k^=40+16+12⇒r→. 4 5 i^+2 j^-3 k^=68⇒r→. 5 i^+2 j^-3 k^=17
Page 29.37 Ex. 29.8
Q1.
Answer :
Let the equation of a plane parallel to the given plane be 2x-3y+z=k … 1This passes through (1, -1, 2). So, 2 1-3 -1+2=k⇒k=7Substituting this in (1), we get2x-3y+z=7, which is the equation of the required plane.
Q2.
Answer :
Let the equation of a plane parallel to the given plane be r→. 2i^-3j^+5k^ = k … 1xi^+yj^+zk^. 2i^-3j^+5k^ = k This passes through (3, 4, -1). So, 3i^+4j^-k^. 2i^-3j^+5k^ = k⇒ k = 6-12-5 = -11Substituting this in (1), we getr→. 2i^-3j^+5k^=-11r→. 2i^-3j^+5k^+11=0, which is the equation of the required plane.
Q3.
Answer :
The equation of the plane passing through the line of intersection of the given planes is2x-7y+4z-3+λ 3x-5y+4z+11=0 … 1This passes through (-2, 1, 3). So,-4-7+12-3+λ -6-5+12+11=0⇒-2+12λ=0⇒λ=16Substituting this in (1), we get2x-7y+4z-3+16 3x-5y+4z+11=0⇒12x-42y+24z-18+3x-5y+4z+11=0⇒15x-47y+28z=7
Q4.
Answer :
The equation of the plane passing through the line of intersection of the given planes isr→. i^+3 j^-k^+λ r→. j^+2 k^=0 r→. i^+3+λ j^+-1+2λk^=0… 1This passes through 2 i^+j^-k^. So,2 i^+j^-k^ i^+3+λ j^+-1+2λk^=0⇒2+3+λ+1-2λ=0⇒λ=6Substituting this in (1), we getr→. i^+3+6 j^+-1+12k^=0⇒r→. i^+9 j^+11 k^=0
Q5.
Answer :
The equation of the plane passing through the line of intersection of the given planes is2x-y+λ 3z-y=0 2x+-1-λy+3λ z=0… 1This plane is perpendicular to 4x+5y-3z=8. So,2 4+-1-λ 5-9λ=0 (Because a1a2+b1b2+c1c2=0)⇒8-5-5λ-9λ=0⇒λ=314Substituting this in (1), we get2x+-1-314y+3314 z=0⇒28x-17y+9z=0
Q6.
Answer :
The equation of the plane passing through the line of intersection of the given planes isx + 2y + 3z – 4 + λ 2x + y – z + 5 = 0 1 + 2λx + 2 + λy + 3 – λz – 4 + 5λ = 0… 1This plane is perpendicular to 5x + 3y – 6z + 8 = 0. So,5 1 + 2λ + 32 + λ – 6 3 – λ = 0 (Because a1a2+b1b2+c1c2=0)⇒5 + 10λ + 6 + 3λ – 18 + 6λ = 0⇒19λ – 7 = 0⇒λ = 719Substituting this in (1), we get1 + 2 719x +2 + 719y + 3 – 719z – 4 + 5 719 = 0⇒33x + 45y + 50z – 41=0
Q7.
Answer :
The equation of the plane passing through the line of intersection of the given planes isx + 2y + 3z + 4 + λ x – y + z + 3 = 0 … 1This passes through (0, 0, 0). So,0 + 0 + 0 + 4 + λ 0 – 0 + 0 + 3 = 0⇒4 + 3λ = 0⇒λ = -4 3Substituting this in (1), we getx + 2y + 3z + 4 – 43x – y + z + 3 = 0 ⇒-x + 10y + 5z = 0⇒x – 10y – 5z = 0
Q8.
Answer :
The equation of the plane passing through the line of intersection of the given planes isx – 3y + 2z – 5 + λ 2x – y + 3z – 1 = 0 … 1This passes through (1, -2, 3). So,1 + 6 + 6 – 5 + λ 2 + 2 + 9 – 1⇒8 + 12λ = 0⇒λ = -2 3Substituting this in (1), we getx – 3y + 2z – 5 – 23 2x – y + 3z – 1 = 0⇒-x – 7y – 13 = 0⇒x + 7y + 13 = 0⇒r→. i^ + 7 j^ + 13 = 0, which is the required vector equation of the plane.
Q9.
Answer :
The equation of the plane passing through the line of intersection of the given planes isx + 2y + 3z – 4 + λ 2x + y – z + 5 = 0 1 + 2λx + 2 + λy + 3 – λz – 4 + 5λ = 0… 1This plane is perpendicular to 5x + 3y + 6z + 8 = 0. So,5 1 + 2λ + 3 2 + λ + 6 3 – λ = 0 (Because a1a2+b1b2+c1c2=0)⇒5 + 10λ + 6 + 3λ + 18 – 6λ = 0⇒7λ + 29 = 0⇒λ = -297Substituting this in (1), we get1 + 2 -297x + 2 – 297y + 3 + 297z – 4 + 5 -297 = 0⇒-51x – 15y + 50z – 173 = 0⇒ 51x + 15y – 50z + 173 = 0
Q10.
Answer :
The equation of the plane passing through the line of intersection of the given planes isr→. i^ + 3 j^ + 6 + λ r→. 3i^ – j^ – 4 k^ = 0 r→. 1 + 3λ i^ + 3 – λ j^ – 4λ k^ + 6 = 0… 1r→. 1 + 3λ i^ + 3 – λ j ^- 4λ k^ = -6r→. -1 – 3λ i^ + λ – 3 j^ + 4λ k^ = 6Dividing both sides by -1-3λ2+λ-32+16λ2, we getr→. -1 – 3λ i^ + λ – 3 j^ + 4λ k^-1 – 3λ2 + λ – 32 + 16λ2 = 6-1 – 3λ2 + λ – 32 + 16λ2, which is the normal form of plane (1), wherethe perpendicular distance of plane (1) from the origin = 6-1 – 3λ2 + λ – 32 + 16λ2⇒1=6-1 – 3λ2 + λ – 32 + 16λ2 (Given)⇒-1 – 3λ2 + λ – 32 + 16λ2 = 6⇒1 + 9λ2 + 6λ + λ2 + 9 – 6λ + 16λ2 = 36⇒26λ2 – 26 = 0⇒λ2 = 1⇒λ = 1 , -1Case 1: Substituting λ = 1 in (1), we getr→. 4 i ^+ 2 j ^- 4 k^ + 6 = 0Case 2: Substituting λ=-1 in (1), we getr→. -2 i^ + 4 j^ + 4 k^ + 6 = 0
Q11.
Answer :
The equation of the plane passing through the line of intersection of the given planes is2x + 3y – z + 1 + λ x + y – 2z + 3 = 0 2 + λx + 3 + λy + -1 – 2λz + 1 + 3λ = 0… 1This plane is perpendicular to 3x – y – 2z – 4 = 0. So,3 2 + λ – 3 + λ – 2 -1 – 2λ = 0 (Because a1a2 + b1b2 + c1c2 = 0)⇒6 + 3λ – 3 – λ + 2 + 4λ = 0⇒6λ + 5 = 0⇒λ = -5 6 Substituting this in (1), we get2 – 56x + 3 – 56y + -1 – 2 -56z + 1 + 3 -56 = 0⇒7X + 13Y + 4z – 9 = 0
Q12.
Answer :
The equation of the plane passing through the line of intersection of the given planes isr→. i^+2 j^+3k^-4+λ r→. 2i^+j^- k^+5=0 r→. 1+2λ i^+2+λ j^+3-λk^-4+5λ=0… 1This plane is perpendicular to r→. 5 i^+3 j^-6 k^+8=0. So,5 1+2λ+3 2+λ-6 3-λ=0 (Because a1a2+b1b2+c1c2=0)⇒5+10λ+6+3λ-18+6λ=0⇒19λ-7=0⇒λ=719Substituting this in (1), we getr→. 1+2 719 i^+2+719 j^+3-719k^-4+5 719=0⇒r→. 33 i^+45 j^+50 k^-41=0⇒x i^+y j^+z k^. 33 i^+45 j^+50 k^-41=0⇒33x+45y+50z-41=0
Q13.
Answer :
Let the equation of a plane parallel to the given plane be r→. i^ + j ^+ k^ = k xi^ + yj^ + zk^. i^ + j ^+ k^ = k … 1This passes through (a, b, c). So, a i^ + b j^ + c k^. i^ + j^ + k^ = k⇒k = a + b + cSubstituting this in (1), we getxi^ + yj^ + zk^. i ^+ j ^+ k^ = a + b + cx + y + z = a + b + c, which is the equation of the required plane.
Q14.
Answer :
The equation of the plane passing through the line of intersection of the given planes isr→. 2 i^ + j ^+ 3 k^ – 7 + λ r→. 2 i^ + 5 j^ + 3 k^ – 9 = 0 r→. 2 + 2λ i^ + 1 + 5λ j^ + 3 + 3λk^ – 7 – 9λ = 0… 1This passes through 2 i^ + j ^+ 3 k^. So,2 i^ + j^ + 3 k^ 2 + 2λ i^ + 1 + 5λ j ^+ 3 + 3λk^ – 7 – 9λ = 0⇒4 + 4λ + 1 + 5λ + 9 + 9λ – 7 – 9λ = 0⇒9λ + 7 = 0⇒λ = -79Substituting this in (1), we getr→. 2 + 2 -7 9 i^ + 1 + 5 -7 9 j^ + 3 + 3 -7 9k^ – 7 – 9 -7 9 = 0⇒r→. 4 i^ – 26 j^ + 6 k^ = 0⇒r→. 2 i^ – 13 j^ + 3 k^ = 0
Page 29.38 Ex. 29.8
Q15.
Answer :
The equation of the plane passing through the line of intersection of the given planes is3x – y + 2z – 4 + λ x + y + z – 2 = 0 … 1This passes through (2, 2, 1). So,6 – 2 + 2 – 4 + λ 2 + 2 + 1 – 2 = 0⇒2 + 3λ = 0⇒λ = -2 3Substituting this in (1), we get3x – y + 2z – 4 – 23 x + y + z – 2 = 0⇒9x – 3y + 6z – 12 – 2x – 2y – 2z + 4 = 0⇒7x – 5y + 4z = 8
Q16.
Answer :
The equation of the plane passing through the line of intersection of the given planes isx + y + z – 1 + λ 2x + 3y + 4z – 5 = 0 1 + 2λx + 1 + 3λy + 1 + 4λz – 1 – 5λ = 0… 1This plane is perpendicular to x – y + z = 0. So,1 + 2λ – 1 1 + 3λ + 1 + 4λ = 0 (Because a1a2 + b1b2 + c1c2 = 0)⇒1 + 2λ – 1 – 3λ + 1 + 4λ = 0⇒3λ + 1 = 0⇒λ = -1 3Substituting this in (1), we get1 + 2 -1 3x + 1 + 3 -1 3y + 1 + 4 -1 3z – 1 – 5 -1 3 = 0⇒x – z + 2 = 0
Q17.
Answer :
The equation of the plane passing through the line of intersection of the given planes isr→. i ^+ j^ + k^ – 6 + λ r→. 2 i^ + 3 j^ + 4 k^ + 5 = 0 r→. 1 + 2λ i^ + 1 + 3λ j^ + 1 + 4λk^ – 6 + 5λ = 0… 1This passes through i ^+ j^ + k^. So,i^ + j^ + k^. 1 + 2λ i^ + 1 + 3λ j^ + 1 + 4λk^ – 6 + 5λ = 0⇒ 1 + 2λ + 1 + 3λ + 1 + 4λ – 6 + 5λ = 0⇒ 14λ – 3 = 0⇒ λ = 314Substituting this in (1), we getr→. 1 + 2 314 i^ + 1 + 3 314 j^ + 1 + 4 314k^ – 6 + 5 314 = 0⇒r→. 20 i^ + 23 j^ + 26 k^ = 69
Page 29.45 Ex. 29.9
Q1.
Answer :
We know that the perpendicular distance of a point P of position vector a→ from the plane r→. n→ = d is given by p = a→. n→-dn→Here,a→ = 2 i^ – j^ – 4 k^; n→ = 3 i^ – 4 j^ + 12 k^; d = 9So, the required distance, p=2 i^ – j ^- 4 k^. 3 i^ – 4 j^ + 12 k^ – 93 i^ – 4 j^ + 12 k^=6 + 4 – 48 – 99 + 16 + 144=-4713=4713 units
Q2.
Answer :
The given plane isr→. 5 i^ + 2 j ^- 7 k^ + 9 = 0⇒r→. -5 i ^- 2 j^ + 7 k^ = 9We know that the perpendicular distance of a point P of position vector a→ from the plane r→. n→ = d is given by p = a→. n→-dn→Finding the distance from i^-j^+3 k^ to the given planeHere,a→ = i^ – j^ + 3 k^; n →= -5 i^ – 2 j ^+ 7 k^; d = 9So, the required distance p is given byp= i^ – j^ + 3 k^. -5 i ^- 2 j ^+ 7 k^ – 9-5 i^ – 2 j^ + 7 k^= -5 + 2 + 21 – 925 + 4 + 49= 9 78= 978 units … (1)Finding the distance from 3 i^+3 j^+3 k^ to the given planeHere, a →= 3 i^ + 3 j^ + 3 k^; n→ = -5 i ^- 2 j^ + 7 k^; d = 9So, the required distance p is given byp=3 i^ + 3 j ^+ 3 k^. -5 i^ – 2 j^ + 7 k^ – 93 i ^+ 3 j^ + 3 k^=-15 – 6 + 21 – 925 + 4 + 49=-978=978 units … (2)From (1) and (2), we can say that the given points are equidistant from the given plane.
Q3.
Answer :
We know that the distance of the point x1, y1, z1 from the plane ax + by + cz + d = 0 is given byax1 + by1 + cz1 + da2 + b2 + c2So, the required distance = 2 + 2 3 – 2 -5 – 912 + 22 + -22= 2 + 6 + 10 – 91 + 4 + 4= 93= 3 units
Q4.
Answer :
The equation of the plane parallel to the given plane isx + 2y – 2z + k = 0 … 1It is given that plane (1) is at a distance of 2 units from (2, 1, 1).⇒2 + 2 – 2 + k12 + 22 + -22 = 2⇒ 2 + k 3 = 2⇒2 + k = 6⇒2 + k = 6; 2 + k = -6⇒k = 4; k = -8Substituting these two values one by one in (1), we getx + 2y – 2z + 4 = 0 andx + 2y – 2z – 8 = 0, which are the equations of the required planes.
Q5.
Answer :
We know that the distance of the point x1, y1, z1 from the plane ax+by+cz+d=0 is given byax1+by1+cz1+da2+b2+c2Distance of the point (1, 1, 1) from the plane 3x + 4y – 12z + 13 = 0The required distance =3 1 + 4 1 – 12 1 + 1332 + 42 + -122=3 + 4 – 12 + 139 + 16 + 144=813 units … (1)Distance of the point (-3, 0, 1) from the plane 3x + 4y – 12z + 13 = 0The required distance =3 -3 + 4 0 – 12 1 + 1332 + 42 + -122=-9+0-12+139+16+144=813 units …. (2)From (1) and (2), we can say that the given points are equidistant from the given plane.
Q6.
Answer :
The equation of the plane parallel to the given plane isx – 2y + 2z + k = 0 … 1It is given that plane (1) is at a distance of 1 unit from (1, 1, 1).⇒1 – 2 + 2 + k12 + -22 + 22 = 1⇒1 + k3 = 1⇒1 + k = 3⇒1 + k = 3; 1 + k = -3⇒k = 2; k = -4Substituting these two values one by one in (1), we getx – 2y + 2z + 2 = 0 andx – 2y + 2z – 4 = 0, which are the equations of the required planes.
Q7.
Answer :
We know that the distance of the point x1, y1, z1 from the plane ax + by + cz + d = 0 is given byax1 + by1 + cz1 + da2 + b2 + c2Equation of the xy- plane is z = 0, which means 0x + 0y + z = 0So, the required distance = 0 2+0 3+ 502+02+12= 51= 5 units
Q8.
Answer :
The given plane isr→. 5 i^ + 2 j^ – 7 k^ + 9 = 0⇒r→. -5 i^ – 2 j^ + 7 k^ = 9We know that the perpendicular distance of a point P of position vector a→ from the plane r→. n→ = d is given by p = a→. n→ – dn→Finding the distance from (3, 3, 3) (which means 3 i^+3 j^+3 k^) to the given planeHere, a →= 3 i^ + 3 j^ + 3 k^; n→ = -5 i^ – 2 j^ + 7 k^; d = 9So, the required distance p = 3 i^ + 3 j^ + 3 k^. -5 i^ – 2 j^ + 7 k^ – 93 i^ + 3 j^ + 3 k^= -15 – 6 + 21 – 925 + 4 + 49= -9 78= 9 78 units
Q9.
Answer :
We know that the distance of the point x1, y1, z1 from the plane ax+by+cz+d=0 is given byax1+by1+cz1+da2+b2+c2Distance of the point (1, 1, 1) from the plane x-y+z+λ=0The required distance =1-1+1+λ12+-12+12=1+λ3 units … (1)Distance of the point (0, 0, 0) from the plane x-y+z+λ=0The required distance =0-0+0+λ12+-12+12=λ3 units … (2)It is given that the product of the distances (1) and (2) is 5.⇒1+λ3 ×λ3 =5⇒λ2+λ-15=0
Q10.
Answer :
Let x, y be a point which is equidistant from the given planes. Then,3x – 4y + 12z – 69 + 16 + 144 = 4x + 3z – 716 + 9⇒3x – 4y + 12z – 613 = ±4x + 3z – 75⇒15x – 20y + 60z – 30 = 52x + 39z – 91; 15x – 20y + 60z – 30 = -52x – 39z + 91⇒37x + 20y – 21
Page 29.46 Ex. 29.9
Q11.
Answer :
The equation of the plane passing through A (3, −1, 2), B (5, 2, 4) and C (−1, −1, 6) ) is
x-3y+1z-25-32+14-2-1-3-1+16-2 = 0 ⇒x-3y+1z-2232-404 = 0⇒12 x-3-16 y+1+12 z-2 = 0⇒3 x-3-4 y+1+3 z-2 = 0⇒3x-4y+3z-19 = 0 … 1We know that the distance of the point x1, y1, z1 from the plane ax+by+cz+d=0 is given byax1+by1+cz1+da2+b2+c2So, the distance of plane (1) from the point P (6, 5, 9) is3 6-4 5+3 9-199+16+9= 634=634 units
Page 29.47 Ex. 29.10
Q1.
Answer :
Multiplying the first equation of the plane by 3, we get6x – 3y + 9z – 12 = 0 6x – 3y + 9z = 12 … 1The second equation of the plane is6x-3y+9z=-13 … 2We know that the distance between two planes ax+by+cz=d1 and ax+by+cz=d2 is d2-d1a2+b2+c2So, the required distance = -13-1262+-32+92=-2536+9+81= 25126=53 14 units
Q2.
Answer :
Let the equation of a plane parallel to the given plane be 2x – 3y + 5z = k … 1This passes through (3, 4, -1). So, 2 3 -3 4+5 -1 = k⇒k = -11Substituting this in (1), we get2x – 3y + 5z =-11… 1, which is the equation of the required plane.The equation of the given plane is2x – 3y + 5z = -7 … 2We know that the distance between two planes ax+by+cz=d1 and ax+by+cz=d2 is d2-d1a2+b2+c2So, the required distance =-7 – -1122 + -32 + 52=-7 + 114 + 9 + 25= 438 units
Q3.
Answer :
We know that the distance between two planes ax+by+cz=d1 and ax+by+cz=d2 is d2-d1a2+b2+c2The equation of plane that is mid-parallel to the planes 2x-2y+z+3=0 … 12x-2y+z+9=0 … 2is of the form 2x-2y+z+k=0 … 3It means that the distance between (1) and (3) = distance between (1) and (2)⇒ k – 3 4 + 4 + 1 = k – 9 4 + 4 + 1⇒k-3 = k-9⇒k-3 = k-9 or k-3 = – k-9⇒3 = 9 (false); k-3 = -k + 9⇒2k = 12⇒k = 6Substituting this in (3), we get 2x-2y+z+6=0, which is the required equation of the plane.
Q4.
Answer :
The given planes arer→. i^+2 j^+3 k^ = -7⇒ x+2y+3z = -7 Multiplying this equation of the plane by 2, we get2x+4y+6z=-14 … (1)andr→. 2 i^ + 4 j^ + 6 k^ = -7⇒2x + 4y + 6z = -7 … 2We know that the distance between two planes ax + by + cz = d1 and ax + by + cz = d2 is d2-d1a2+b2+c2So, the required distance = -7 – -1422 + 42 + 62= 7 4 + 16 + 36= 756 units
Page 29.57 Ex. 29.11
Q1.
Answer :
We know that the angle θ between the line r→ = a→ + λ b→ and the plane r→. n→=d is given bysin θ = b→. n→b→ n→.Here, b →= 2 i^+3 j^+4 k^ and n→ = i^+j^+k^So, sin θ = 2 i^+3 j^+4 k^. i^+j^+k^2 i^+3 j^+4 k^ i^+j^+k^ = 2+3+44+9+16 1+1+1 = 929 3 = 3 329⇒θ = sin-1 3 329
Q2.
Answer :
The given line is parallel to the vector b→ = i^ – j ^+ k^ and the given plane is normal to the vector n→=2 i^ + j ^- k^.We know that the angle θ between the line and the plane is given bysin θ = b→. n→b→ n→= i^-j^+k^. 2 i^+j^-k^i^-j^+k^ 2 i^+j^-k^ = 2-1-11+1+1 4+1+1 = 0⇒θ=sin-1 0=0
Q3.
Answer :
It is given that the line passes through A 3, -4, -2 and B 12, 2, 0.So, b→ = AB→=OB→-OA →= 12 i^+2 j^+0 k^-3 i^-4 j^-2 k^ = 9 i^+6 j^+2 k^The given line is parallel to the vector b→=9 i^+6 j^+2 k^ and the given plane is normal to the vector n→=3 i^-j^+k^.We know that the angle θ between the line and the plane is given bysin θ=b→. n→b→ n→=9 i^+6 j^+2 k^. 3 i^-j^+k^9 i^+6 j^+2 k^ 3 i^-j^+k^ = 27 – 6 + 281 + 36 + 4 9 + 1 + 1 = 2311 11⇒θ=sin-1 2311 11
Q4.
Answer :
The given line is parallel to the vector b→ = 2 i^ – m j^ – 3 k^ and the given plane is normal to the vector n→ = m i^ + 3 j^ + k^.If the line is parallel to the plane, the normal to the plane is perpendicular to the line.⇒b→ ⊥ n→⇒b→. n→ = 0⇒2 i^ – m j^ – 3 k^. m i^ + 3 j^ + k^ = 0⇒2m – 3m – 3 = 0⇒-m – 3 = 0⇒ m = -3
Q5.
Answer :
The given plane passes through the point with position vector a→=2 i^+5 j^+7 k^ and is parallel to the vector b→=i^+3 j^+4 k^. The given plane is r→. i ^+ j^-k^ = 7 or . ccSo, the normal vector, n →= i^+j^- k^ and d=7.Now, b→. n→=i^ + 3 j^ + 4 k^. i ^+ j ^- k^ = 1 + 3 – 4 = 4 – 4 = 0So, b→ is perpendicular to n→.So, the given line is parallel to the given plane.The distance between the line and the parallel plane . Then,d = length of the perpendicular from the point a→=2 i^+5 j^+7 k^ to the plane r→. n→ = dd=a→. n→-dn→=2 i^ + 5 j ^+ 7 k^. i^ + j ^- k^ – 7 i^ + j ^- k ^=2+5-7-71+1+1= 73 units
Q6.
Answer :
The required line is perpendicular to the plane r→. i^ – 2 j ^+ 3 k^ = 3. Therefore, it is parallel to the normal i^ + 2 j^ + 3 k^. Thus, the required line passes through the point with position vector a→ = 0 i^+0 j^+0 k^ and is parallel to the vector n→ = i^ – 2 j^ + 3 k^.So, its vector equation isr→ = a→ + λ n^⇒r→ = 0 i^ + 0 j^ + 0 k ^+ λ i^ – 2 j^ + 3 k^⇒r→= λ i^ – 2 j ^+ 3 k^
Q7.
Answer :
The equation of the plane through (2, 3, -4) isa x-2 + b y-3 + c z+4 = 0 … 1This plane passes through (1, -1, 3). So,a 1 – 2 + b -1 – 3 + c 3 + 4=0⇒-a – 4b + 7c = 0 … 2Again plane (1) is parallel to x-axis. It means that plane (1) is perpendicular to the yz-plane whose equation is x = 0 or 1. x + 0. y + 0. z = 0⇒a 1 + b 0 + c 0 = 0 … 3 (Because a1a2+b1b2+c1c2=0)Solving (1), (2) and (3), we getx-3y-3z+4-1-47100=0⇒0 x – 3 + 7 y – 3 + 4 z + 4 = 0⇒7y + 4z – 5 = 0
Q8.
Answer :
The equation of the plane through (0,0, 0) isa x-0+b y-0+c z-0=0 ax+by+cz=0… 1This plane passes through (3, -1, 2). So,3a-b+2c=0 … 2Again plane (1) is parallel to the given line. It means that the normal to plane (1) is perpendicular to the line.⇒a 1+b -4+c 7=0 … 3 (Because a1a2+b1b2+c1c2=0)Solving (1), (2) and (3), we getx y z3-1 21-4 7 = 0⇒x – 19y – 11z = 0
Q9.
Answer :
Let the direction ratios of the required line be proportional to a, b, c. As it passes through (1, 2, 3), its equations arex-1a = y-2b = z-3c … 1It is given that (1) is parallel to the planes r→. i^-j^+2 k^ = 5 and r→. 3 i^+j^+2 k^ = 6 or x – y + 2z = 5 and 3x + y + 2z = 6⇒a – b + 2c = 0 … 23a + b + 2z = 0 … 3Solving these two by cross-multiplication method, we geta-2-2 = b6-2 = c1+3⇒a-4 = b4 = c4⇒a1 = b-1 = c-1 = λ(say)⇒a = λ; b = -λ; c = -λSubstituting these values in (1), we getx-11=y-2-1=z-3-1, which is the Cartesian form of the required line.Vector formThe given line passes through a point whose position vector is a→=i^+2 j^+3 k^ and is parallel to the vector b→ = i^- j ^+ k^. So, its equation in vector form isr→=a→+λb→⇒r→=i^+2 j^+3 k^+λi^-j^+k^
Disclaimer: The answer given for this problem in the text book is incorrect. The problem should be same as problem #19 to get the text book answer.
Q10.
Answer :
Let a, b, c be the direction ratios of the line of section of the given planes.As this line lies on both the planes, their normals are perpendicular to it.⇒5a+2b-4c=0 …12a+8b+2c=0⇒a+4b+c=0 …⇒2Using cross-multiplication method, we geta2+16=b-4-5=c20-2⇒a18=b-9=c18⇒a2=b-1=c2So, the direction ratios of the line are proportional to 2, -1, 2.Direction ratios of the given line are 4,-2, -5.Now,2 4+-1 -2+2 -5=8+2-10=0So, the line of section of the given planes is parallel to the given plane.
Q11.
Answer :
Let a, b, c be the direction ratios of the given line.Since the line passes through the point (1, -1, 2) isx-1a = y+1b = z-2c …1Since this line is perpendicular to the plane 2x-y+3z-5=0, the line is parallel to the normal of the plane.So, the direction ratios of the line are proportional to the direction ratios of the given plane.So, a2 = b-1 = c3 = λ⇒a = 2λ; b = -λ; c = 3λSubstituting these values in (1), we getx-12=y+1-1=z-23, which is the Cartesian form of the line.Vector formThe given line passes through a point whose position vector is a→ = i ^- j^ + 2 k^ and is parallel to the vector b→ = 2 i ^- j ^+ 3 k^. So, its equation in vector form isr →= a→ + λb→⇒r→ = i^ – j^ + 2 k^ + λ2 i^ – j^ + 3 k^
Q12.
Answer :
The equation of the plane through (2, 2, -1) isa x – 2 + b y – 2 + c z + 1 = 0 … 1This plane passes through (3, 4, 2). So,a 3 – 2 + b 4 – 2 + c 2 + 1 = 0⇒a + 2b + 3c = 0 … 2 Again plane (1) is parallel to the line whose direction ratios are 7, 0, 6.It means that the normal of plane (1) is perpendicular to the line whose direction ratios are 7, 0, 6.⇒7a+0b+6c=0 (Because a1a2+b1b2+c1c2=0)Solving (1), (2) and (3), we getx-2y-2z+1123706=0⇒12 x-2+15 y-2-14 z+1=0⇒12x+15y-14z-68=0
Q13.
Answer :
The given line is parallel to the vector b→=3 i^-j^+2 k^ and the given plane is normal to the vector n→=3 i^+4 j^+k^.We know that the angle θ between the line and the plane is given bysin θ=b→. n→b→ n→=3 i^-j^+2 k^. 3 i^+4 j^+k^3 i^-j^+2 k^ 3 i^+4 j^+k^ = 9-4+29+1+4 9+16+1 = 714 26 =72 7 2 13 = 752=752⇒θ=sin-1 752
Q14.
Answer :
The equation of the plane passing through the intersection of the given planes isx-2y+z-1+λ 2x+y+z-8 = 0⇒1+2λ x+-2+λ y+1+λ z-1-8λ = 0 … 1This plane is parallel to the line whose direction ratios are proportional to 1,2,1.So, the normal to the plane is perpendicular to the line whose direction ratios are proportional to 1, 2, 1.⇒1+2λ 1+-2+λ 2+1+λ 1 = 0⇒1+2λ-4+2λ+1+λ = 0⇒5λ-2 = 0⇒λ = 25Substituting this in (1), we get1+2 25 x+-2+25 y+1+25 z-1-8 25 =0⇒9x-8y+7z-21=0… 2, which is the required equation of the plane.Perpendicular distance of plane (2) from (1, 1, 1)=9 1 – 8 1 + 7 1 – 2192 + -82 + 72= -13194=13194 units
Q15.
Answer :
The given plane passes through the point with position vector a→= i^+j^+0 k^ and is parallel to the vector b→=3 i^- j^+2 k^. The given plane is r→. 2j^+k^=3 or r→. n→=dSo, normal vector, n→=0 i^+2 j^+k^ and d=3Now, b→. n→=3 i^- j^+2 k^. 0 i^+2 j^+k^=0-2+2=0So, b→ is perpendicular to n→.Hence,the given line is parallel to the given plane.The distance between the line and the parallel plane is the distance between any point on the line and the given plane. The plane passes through the point a→= i^+j^+0 k^.The perpendicular distance from the given line to the plane isd=a→. n→-dn→=i^ + j^ + 0 k^. 0 i^ + 2 j^ + k^ -30 i^ + 2 j^ + k^=0 + 2 + 0 -30 + 22 + 12= 15 units
Q16.
Answer :
The given plane passes through the point with position vector a→=- i^ + j^ + k^ and is parallel to the vector b→ = 2 i^+j^+4 k^. The given plane is r→. i^ + 2 j^ – k^ = 1 or r→. n→ = d.So, normal vector, n→ = i^+2 j^-k^ and d = 1Now, b→. n→ = 2 i^ + j^ + 4 k^. i^ + 2 j ^- k^ = 2 + 2 – 4 = 0So, b→ is perpendicular to n→.So, the given line is parallel to the given plane.The distance between the line and the parallel plane is the distance between any point on the line and the given plane. Since the plane passes through the point a→=- i^ + j^ + k,^the perpendicular distance from the given line to the plane isd=a→. n→-dn→=- i^ + j^ + k^. i ^+ 2 j^ – k^ – 1i^ + 2 j^-k^=-1 + 2 -1-11 + 4 + 1= 16 units
Page 29.58 Ex. 29.11
Q17.
Answer :
The equation of the plane passing through the intersection of the given planes is3x-4y+5z-10 + λ 2x+2y-3z-4 = 0⇒3+2λ x+-4+2λ y+5-3λ z-10-4λ = 0 … 1The given line isx = 2y = 3zDividing this equation by 6, we getx6=y3=z2The direction ratios of this line are proportional to 6, 3, 2.So, the normal to the plane is perpendicular to the line whose direction ratios are proportional to 6, 3, 2.⇒3+2λ 6 + -4 + 2λ 3 + 5 – 3λ 2 = 0⇒18 + 12λ – 12 + 6λ + 10 – 6λ = 0⇒12λ + 16 = 0⇒λ =-4 3Substituting this in (1), we get3+2-4 3 x + -4+2 -4 3 y + 5-3 -4 3 z – 10 – 4 -4 3 = 0⇒x – 20y + 27z = 14
Q18.
Answer :
Let a, b, c be the direction ratios of the given line.Since the line passes through the point (1, 2, 3) is,x-1a = y-2b = z-3c …1Since this line is perpendicular to the plane r→. i^+2 j^-5 k^+9 = 0 or x+2y-5z+9 = 0, the line is parallel to the normal of the plane.So, the direction ratios of the line are proportional to the direction ratios of the given plane.So, a1= b2 = c-5 = λ⇒a = λ; b = 2λ; c = -5λSubstituting these values in (1), we getx-11 = y+12 = z-2-5, which is the Cartesian form of the line.Vector formThe given line passes through a point whose position vector is a →= i^+2 j^+3 k^ and is parallel to the vector b→ = i^ + 2 j^- 5 k^. So, its equation in vector form isr→=a→+λb→⇒r→=i^+2 j^+3 k^+λi^ + 2 j^ – 5 k^
Q19.
Answer :
Let the direction ratios of the required line be proportional to a, b, c. As it passes through (1, 2, 3), its equation becomesx-1a=y-2b=z-3c … 1It is given that (1) is parallel to the planes r→. i^ – j^ + 2 k^ = 5 and r→. 3 i^ + j^ + 2 k^ = 6 or x – y + 2z = 5 and 3x + y + 2z = 6. So,a – b + 2c = 0 … 23a + b + c = 0 … 3Solving these two by cross-multiplication method, we geta-1-2 = b6-1 = c1+3⇒a-3 = b5 = c4 = λ(say)⇒a =-3λ; b = 5λ; c = 4λSubstituting these values in (1), we getx-1-3 = y-25 = z-34, which is the Cartesian form of the required line.Vector formThe given line passes through a point whose position vector is a→ = i^ + 2 j^ + 3 k^ and is parallel to the vector b→ = -3 i^ + 5 j ^+ 4 k^. So, its equation in vector form isr →= a→ + λb→⇒r →= i^+2 j^+3 k^ + λ-3i^+5 j^+4 k^
Q20.
Answer :
The equation of the plane passing through the point (3,4, 1) isa x-3+b y-4+c z-1=0 … 1This plane passes through (0, 1, 0). So,a 0-3 + b 1-4 + c 0-1 = 0⇒-3a – 3b – c = 0⇒ 3a + 3b + c = 0 … 2Again plane (1) is parallel to the given line. It means that the normal to plane (1) is perpendicular to the line.⇒a 2+b 7+c 5=0 … 3 (Because a1a2+b1b2+c1c2=0)Solving (1), (2) and (3), we getx-3y-4z-1331275 = 0⇒8 x – 3 – 13 y – 4 + 15 z – 1 = 0⇒8x – 13y + 15z + 13 = 0
Q21.
Answer :
The equation of the plane passing through the line of intersection of the given planes isr→. i^+2 j^+3k^-4+λ r→. 2i^+j^- k^+5=0 r→. 1+2λ i^+2+λ j^+3-λk^-4+5λ=0… 1This plane is perpendicular to r→. 5 i^+3 j^-6 k^+8=0. So,5 1+2λ+3 2+λ-6 3-λ=0 (Because a1a2+b1b2+c1c2=0)⇒5 + 10λ + 6 + 3λ – 18 + 6λ = 0⇒19λ – 7 = 0⇒λ = 719Substituting this in (1), we getr→. 1 + 2 719 i ^+ 2 + 719 j ^+ 3 – 719k^ – 4 + 5 719 = 0⇒r→. 33 i ^+ 45 j^ + 50 k^ = 41
Q22.
Answer :
Let x-23 = y+14 = z-22 = λ (say)⇒x = 3λ + 2; y = 4λ – 1; z = 2λ + 2 … 1Since (x, y, z) intersects the plane x – y + z – 5 = 0,3λ + 2 – 4λ – 1 + 2λ + 2 – 5 = 0⇒3λ + 2 – 4λ + 1 + 2λ + 2 – 5 = 0⇒λ = 0Substituting this in (1), we getx = 2; y = -1; z = 2So, x, y, z = 2, -1, 2Finding the angleThe given line is parallel to the vector b→=3 i^+4 j^+2 k^ and the given plane is normal to the vector n→=i^-j^+k^.We know that the angle θ between a line and a plane is given bysin θ=b→. n→b→ n→=3 i^+4 j^+2 k^. i^-j^+k^3 i^+4 j^+2 k^ i^-j^+k^ = 3 – 4 + 29 + 16 + 4 1 + 1 + 1 = 187⇒θ=sin-1 187
Q23.
Answer :
Let a, b, c be the direction ratios of the given line.Since the line passes through the point (1, 2, 3) is,x-1a = y-2b = z-3c …1Since this line is perpendicular to the planer→. i^ + 2 j^ – 5 k^ + 9 = 0 or x + 2y – 5z + 9 = 0, the line is parallel to the normal of the plane.So, the direction ratios of the line are proportional to the direction ratios of the given plane.So, a1 = b2 = c-5 = λ⇒a = λ; b = 2λ; c = -5λSubstituting these values in (1), we getx-11 = y+12 = z-2-5, which is the Cartesian form of the line.Vector formThe given line passes through a point whose position vector is a→ = i^ + 2 j ^+ 3 k^ and is parallel to the vector b→ = i^ + 2 j^ – 5 k^. So, its equation in vector form isr→ = a→ + λb→⇒r→ = i^ + 2 j^ + 3
Q24.
Answer :
The given line is parallel to the vector b→=2 i^+3 j^+6 k^ and the given plane is normal to the vector n→=10 i^+2 j^-11 k^.We know that the angle θ between the line and the plane is given bysin θ=b→. n→b→ n→=2 i^+3 j^+6 k^. 10 i^+2 j^-11 k^2 i^+3 j^+6 k^ 10 i^+2 j^-11 k^ = 20 + 6 – 664 + 9 + 36 100 + 4 + 121 = -407 15 = -821⇒θ = sin-1 -821
Q25.
Answer :
Let the direction ratios of the required line be proportional to a, b, c. It passes through (1, 2, 3). So its equations arex-1a = y-2b = z-3c … 1It is given that (1) is parallel to the planes r→. i^-j^+2 k^ = 5 and r→. 3 i^+j^+2 k^ = 6 or x-y+2z=5 and 3x+y+2z=6Thus,a-b+2c = 0 … 2 3a + b + z = 0 … 3Solving these two by cross-multiplication method, we geta-1-2 = b6-1 = c1+3⇒a-3 = b5 = c4 = λ(say)⇒a = -3λ; b = 5λ; c = 4λSubstituting these values in (1), we getx-1-3 = y-25 = z-34, which is the Cartesian form of the required line.
Q26.
Answer :
Direction ratios of the given line are proportional to 6, λ, -4.Direction ratios of the plane are 3, -1, -2.Since the given line is parallel to the given plane, the line is perpendicular to the normal of the given plane.⇒6 3+λ -1+-4 -2=0⇒18-λ+8=0⇒λ=26
Page 29.61 Ex. 29.12
Q1.
Answer :
i) The equation of the line through the points (5, 1, 6) and (3, 4, 1) isx-53-5 = y-14-1 = z-61-6⇒x-5 -2 = y-13 = z-6-5The coordinates of any point on this line are of the formx-5-2 = y-13 = z-6-5 = λ⇒x = -2λ+5; y = 3λ+1; z = -5λ+6So, the coordinates of the point on the given line are -2λ+5, 3λ+1, -5λ+6. Since this point lies on the YZ- plane, x = 0⇒-2λ + 5 = 0⇒λ = 52So, the coordinates of the point are-2λ+5, 3λ+1, -5λ+6=-2 52+5, 3 52+1, -5 52+6=0, 172, 132
ii) The equation of the line through the points (5, 1, 6) and (3, 4, 1) isx-53-5=y-14-1=z-61-6⇒x-5-2=y-13=z-6-5The coordinates of any point on this line are of the formx-5-2=y-13=z-6-5=λ⇒x=-2λ+5; y=3λ+1; z=-5λ+6So, the coordinates of the point on the given line are -2λ+5, 3λ+1, -5λ+6. Since this point lies on the ZX – plane, y=0⇒3λ+1=0⇒λ=-13So, the coordinates of the point are-2λ+5, 3λ+1, -5λ+6=-2 -13+5, 3 -13+1, -5 -13+6=173, 0, 233
Q2.
Answer :
The equation of the line through the points (3, -4, -5) and (2, -3, 1) isx-32-3 = y+4-3+4 = z+51+5⇒x-3-1 = y+41 = z+56The coordinates of any point on this line are of the formx-3-1 = y+41 = z+56 = λ⇒x = -λ+3; y = λ-4; z = 6λ-5So, the coordinates of the point on the given line are -λ+3, λ-4, 6λ-5. Since this point lies on the plane 2x + y + z = 7,2 -λ+3 + λ-4 + 6λ-5 = 7⇒-2λ + 6 + λ – 4 + 6λ – 5 = 7⇒ 5λ = 10⇒ λ = 2So, the coordinates of the point are-λ+3, λ-4, 6λ-5=-2+3, 2-4, 6 2-5=1, -2, 7
Q3.
Answer :
The given equation of the line isr→=2 i^-j^+2 k^+λ 3 i^+4 j^+2 k^⇒r→=2+3λ i^+-1+4λ j^+2+2λ k^The coordinates of any point on this line are of the form 2 + 3λ i^ + -1 + 4λ j^ + 2 + 2λ k^. or 2 + 3λ, -1 + 4λ, 2 + 2λSince this point lies on the plane r→. i^ – j ^+ k^ = 5, 2+3λ i^+-1+4λ j^+2+2λ k^. i^-j^+k^ = 5⇒2+3λ+1-4λ+2+2λ-5=0⇒λ=0So, the coordinates of the point are2+3λ, -1+4λ, 2+2λ=2+0, -1+0, 2+0=2, -1, 2Distance between (2, -1, 2) and (-1, -5, -10)=-1-22+-5+12+-10-22=9+16+144=13 units
Page 29.68 Ex. 29.13
Q1.
Answer :
We know that the lines r→=a1→+λ b1→ and r→=a2→+μ b2→ are coplanar if a1→. b1→×b2→ = a2→. b1→×b2→ and the equation of the plane containing them isr→. b1→×b2→ = a1→. b1→×b2→.Here,a1 →= 0 i^+2 j^-3 k^; b1→ = i^+2 j^+3 k^; a2→ = 2 i^+6 j^+3 k^; b2→ = 2 i^+3 j^+4 k^b1→×b2 →= i^j^k^123234 = -i^+2 j^-k^a1→. b1→×b2→ = 0 i^+2 j^-3 k^. -i^+2 j^-k^ = 0 + 4 + 3 = 7a2→. b1→×b2→ = 2 i^ + 6 j^ + 3 k^. -i^ + 2 j ^- k^ = -2 + 12 – 3 = 7Clearly, a1→. b1→×b2→=a2→. b1→×b2→Hence, the given lines are coplanar.The equation of the plane containing the given lines isr→. b1→×b2→ = a1→. b1→×b2→⇒r→. -i^+2 j^-k^ = 0 i^ + 2 j^ – 3 k^. -i ^+ 2 j^ – k^⇒r→. -i^ + 2 j^ – k^ = 7⇒r→. i^ – 2 j^ + k^ + 7 = 0
Q2.
Answer :
We know that the linesx-x1l1=y-y1m1=z-z1n1 and x-x2l2=y-y2m2=z-z2n2 are coplanar ifx2-x1y2-y1z2-z1l1m1n1l2m2n2 = 0and the equation of the plane containing these lines isx-x1y-y1z-z1l1m1n1l2m2n2 = 0Here,x1=-1; y1=3; z1=-2; x2= 0; y2 = 7; z2=-7; l1=-3; m1 = 2; n1=1; l2=1; m2=-3; n2=2Now,0+17-3-7+2-3211-32=14-5-3211-32=1 7 – 4 -7 – 5 7=7 + 28 – 35=0So, the given lines are coplanar.The equation of the plane containing the given lines isx+1y-3z+2-3211-32=0⇒x+1 7 – y-3 -7 + z+2 7 = 0⇒7x + 7y + 7z = 0⇒x + y + z = 0
Q3.
Answer :
Let the equation of the plane passing through (0, 7, -7) bea x-0 + b y-7 +c z+7 = 0 … 1The line x+1-3 = y-32 = z+21 passes through (-1, 3, -2) and its direction ratios are proportional to -3, 2, 1. Since plane (1) contains this line, it must pass through the point (-1, 3, -2).⇒a -1-0 + b 3-7+c -2+7 = 0 ⇒-a -4b + 5c = 0⇒a + 4b – 5c = 0… 2Since plane (1) contains this line, it must be parallel to the line.⇒-3a+2b+c=0 … 3Solving (1), (2) and (3), we getx-0y-7z+714-5-321 = 0⇒14x + 14 y – 7 + 14 z + 7 =0⇒14x + 14y + 14z = 0⇒x + y + z = 0
Q4.
Answer :
We know that the equation of the plane containing two given parallel lines x-x1a = y-y1b = z-z1c and x-x2a = y-y2b = z-z2c isx-x1y-y1z-z1x2-x1y2-y1z2-z1a b c=0Here,x1 = 4; y1 = 3; z1 = 2; x2 = 3; y2 = -2; z2 = 0; l1 = 1; m1 = -4; n1 = 5; l2 = 1; m2 = -4; n2 = 5Now,x-4y-3z-23-4-2-30-21-45 = 0⇒x-4y-3z-23-4-2-3 0-21-45 = 0⇒-33 x-4 + 3 y-3 + 9 z-2 = 0⇒11 x-4 – y-3 – 3 z-2 = 0⇒11x-y-3z = 35
Q5.
Answer :
The equation of the given line isx+43 = y+65 = z-1-2The coordinates of any point on this line are of the formx+43 = y+65 = z-1-2 = λ⇒x = 3λ-4; y = 5λ-6; z = -2λ+1So, the coordinates of the point on the given line are 3λ-4, 5λ-6, -2λ+1. Since this point lies on the plane 3x – 2y + z + 5 = 0,3 3λ – 4 – 2 5λ – 6 + -2λ + 1 + 5 = 0⇒9λ – 12 – 10λ + 12 – 2λ + 1 + 5 = 0⇒-3λ + 6 = 0⇒λ = 2So, the coordinates of the point are3λ – 4, 5λ – 6, -2λ + 1=3 2 – 4, 5 2 – 6, -2 2 + 1=2, 4, -3Substituting this point in another plane equation 2x+3y+4z-4=0, we get2 2+3 4+4 -3-4=0⇒4+12-12-4=0⇒0=0So, the point (2, 4, -3) lies on another plane too. So, this is the point of intersection of both the lines.Finding the plane equationLet the direction ratios be proportional to a, b, c.Since the plane contains the line x+43= y+65 = z-1-2, it must pass through the point (-4, -6, 1) and is parallel to this line.So, the equation of plane isa x + 4 + b y + 6 + c z – 1 = 0 …1and3a + 5b – 2c = 0… 2Since the given plane contains the planes 3x – 2y + z + 5 = 0 = 2x + 3y + 4z – 4, 3a – 2b + c = 0 … 32a + 3b + 4z = 0 … 4Solving (3) and (4) using cross-multiplication, we geta-11 = b-10 = c13… 5Using (1), (2) and (5), the equation of plane is x+4 y+6 z-135-21110-13 = 0⇒-45 x+4+17 y+6-25 z-1=0⇒45 x+4-17 y+6+25 z-1=0⇒45x-
Q6.
Answer :
The line r→=i^+j^+0 k^+λ 2 i^+j^+4 k^….(1) passes through a point whose position vector is a→=i^+j^+0 k^ and is parallel to the vector b→=2 i^+j^+4 k^.If the plane r→. i^+2 j^-k^=3 contains the given line, then (1) it should passes through the point i^+j^+0 k^ (2) it should be parallel to the lineNow, i^+j^+0 k^. i^+2 j^-k^ = 1 + 2 = 3So, the plane passes through the point i^+j^+0 k^.The normal vector to the given plane is n →= i^+ 2 j^ – k.^We observe thatb→. n→ = 2 i^ + j ^+ 4 k^. i^ + 2 j^ – k^ = 2 + 2 – 4 = 0Therefore, the plane is parallel to the line.Hence, the given pla
Q7.
Answer :
The given equations of the lines arex+33 = y-2 = z-76… 1x+61 = y+5-3 = z-12… 2Let the direction ratios of the plane be proportional to a, b, c.Since the plane contains line (1), it should pass through (-3, 0, 7) and is parallel to the line (1).Equation of the plane through (1) isa x + 3 + b y + c z – 7 = 0 … 3,where 3a – 2b + 6c = 0 … 4Since the plane contains line (2), the plane is parallel to line (2) also.⇒a – 3b + 2c = 0 … 5Solving (4) and (5) using cross-multiplication, we geta14 = b0 = c-7Substituting a, b and c in (3), we get14 x + 3 + 0 y – 7 z – 7 = 0⇒2 x + 3 + 0 y – 1 z – 7 = 0⇒2x – z + 13 = 0
Q8.
Answer :
The equation of any plane passing through (3, 4, 2) isa x-3 + b y-4 + c z-2 = 0 … 1It is given that (1) is passing through (7, 0, 6). So,a 7-3 + b 0-4 + c 6-2 = 0 ⇒4a – 4b + 4c = 0⇒a – b + c = 0 … 2It is given that (1) is perpendicular to the plane 2x – 5y + 0z + 15z = 0. So,2a – 5b + 0c = 0 … 3Solving (1), (2) and (3), we getx-3y-4z-21-112-50=0⇒5 x-3 + 2 y-4 -3 z-2 = 0⇒5x + 2y – 3z = 17Or r→. 5 i^ + 2 j^ – 3 k^ = 17Showing that the plane contains the lineThe line r→=i^+3 j^-2 k^+λ i^-j^+k^ passes through a point whose positon vector is a→ = i^ + 3 j^-2 k^ and is parallel to the vector b →= i ^- j ^+ k^.If the plane r→. 5 i^+2 j^-3 k^=17 contains the given line, then (1) it should pass through the point i^+3 j^-2 k^ (2) it should be parallel to the lineNow, i^+3 j^-2 k^. 5 i^+2 j^-3 k^= 5 + 6 + 6 = 17So, the plane passes through the point i^ + 3 j ^- 2 k^.The normal vector to the given plane is n →= i ^- j^ + k.^We observe thatb→. n→=i^-j^+k^. 5 i^+2 j^-3 k^ = 5 – 2 – 3 = 0Therefore, the plane is parallel to the line.Hence, the given plane contains the given line.
Page 29.69 Ex. 29.13
Q9.
Answer :
We know that the linesx-x1l1 = y-y1m1 = z-z1n1 and x-x2l2 = y-y2m2 = z-z2n2 are perpendicular ifl1l2 + m1m2 + n1n2 = 0Here,l1 = -3; m1=-2k; n1= 2; l2 = k; m2 = 1; n2 = 5It is given that given lines are perpendicular.⇒l1l2+m1m2+n1n2 = 0⇒-3 k + -2k 1 + 2 5 = 0⇒-3k – 2k + 10 = 0⇒-5k = -10⇒ k = 2Substituting this value in the given equations of the lines, we getx-1-3 = y-2-4 = z-32… 1 x-12 = y-21 = z-35 … 2Finding the equation of the planeLet the direction ratios of the required plane be proportional to a, b, c.We know from (1) and (2) that lines (1) and (2) pass through the point (1, 2, 3) and the direction ratios of (1) and (2) are proportional to -3, -4, 2 and 2, 1, 5 respectively.Since the plane contains the lines (1) and (2), the plane must pass through the point (1, 2, 3) and it must be parallel to the line.So, the equation of the plane isa x – 1 + b y – 2 + c z – 3 = 0 … 3-3a – 4b + 2c = 0 … 42a + b + 5c = 0 … 5Solving (1), (2) and (3), we getx-1y-2z-3-3-42215=0⇒-22 x-1 + 19 y-2 + 5 z-3 = 0⇒-22x + 19y + 5z = 31
Q10.
Answer :
The coordinates of any point on this line are of the formx-23=y+14=z-22=λ⇒x = 3λ + 2; y = 4λ – 1; z = 2λ + 2So, the coordinates of the point on the given line are 3λ + 2, 4λ – 1, 2λ + 2. This point lies on the plane x – y + z – 5 = 0.⇒3λ + 2 – 4λ + 1 + 2λ + 2 – 5 = 0⇒λ = 0So, the coordinates of the point are3λ + 2, 4λ – 1, 2λ + 2=3 0 + 2, 4 0 – 1, 2 0 + 2=2, -1, 2Finding the angle between the line and the planeThe given line is parallel to the vector b→=3 i^+4 j^+2 k^ and the given plane is normal to the vector n→=i ^- j^ + k^.We know that the angle θ between the line and the plane is given bysin θ=b→. n→b→ n→=3 i^ + 4 j^ + 2 k^. i^ – j^ + k^3 i^ + 4 j^ + 2 k^ i^ – j ^+ k^ = 3 – 4 + 29 + 16 + 4 1 + 1 +1 = 187⇒θ = sin-1 187
Q11.
Answer :
Let A (1, 1 , -2), B (2, -1, 1) and C (1, 2, 1) be the points represented by the given position vectors.The required plane passes through the point A (1, 1, -1) whose position vector is a→=i^ + j^ – 2 k^ and is normal to the vector n→ given byn→=AB→ × AC.→Clearly, AB→=OB→ -OA →= 2 i^- j^+k^-i^ + j^ – 2 k^ = i^-2 j^+3 k^AC→=OC→-OA→=i^+2 j^+k^-i^+ j^-2 k^=0 i^+ j^+3 k^n→=AB→×AC→=i^j^k^1-23013=-9 i^-3 j^ +k^The vector equation of the required plane isr→. n→=a→. n→⇒r→. -9 i^-3 j^ +k^=i^+ j^-2 k^. -9 i^-3 j^ +k^⇒r→. -9 i^-3 j^ +k^=-9-3-2⇒r→. -9 i^+3 j^ -k^=-14⇒r→. 9 i^+3 j^ -k^=14To find the point of intersection of this plane The given equation of the line isr→=3 i^-j^-k^+λ 2 i^-2 j^+k^⇒r→=3+2λ i^+-1-2λ j^+-1+λ k^The coordinates of any point on this line are in the form of 3 + 2λ i ^+ -1 – 2λ j ^+ -1 + λ k^ or 3 + 2λ, -1 – 2λ, -1 + λSince this point lies on the plane r→. 9 i^ + 3 j^ -k^= 14,3 + 2λ i^ + -1 – 2λ j ^+ -1 + λ k^. 9 i^ + 3 j^ -k^ = 14⇒27 + 18λ – 3 – 6λ + 1 – λ = 14⇒11λ =-11⇒λ =-1So, the coordinates of the point are3 + 2λ, -1 – 2λ, -1 + λ=3 – 2, -1 + 2, -1 – 1=1, 1, -2
Page 29.70 Ex. 29.14
Q1.
Answer :
The given equations of the lines arex-2-1 = y-52 = z-03… 1x-02 = y+1-1 = z-12… 2Clearly (2) passes through the point P (0, -1, 1).Let the direction ratios of the plane be proportional to a, b, c.Since the plane containing line (1) should pass through (2, 5, 0) and is parallel to the line (1),equation of the plane passing through (1) isa x-2 + b y-5 + c z-0 = 0 … 3,where -a + 2b + 3c = 0 … 4Since the plane is parallel to line (2),2a – b + 2c = 0 … 5Solving (4) and (5) using cross-multiplication, we geta7 = b8 = c-3Substituting a, b and c in (3), we get7 x-2 + 8 y-5 – 3 z-0 = 0⇒7x + 8y – 3z – 54 = 0 … 6,which is the equation of the plane containing line (1) and parallel to line (2).Shortest distance between (1) and (2)=Distance between the point P (0, -1, 1) and plane (6)=7 0+8 -1-3 1-5449+64+9=65122 units
Q2.
Answer :
The given equations of the lines arex+17 = y+1-6 = z+11… 1x-31 = y-5-2 = z-71… 2Clearly (2) passes through the point P (3, 5, 7).Let the direction ratios of the plane be proportional to a, b, c.Since the plane contains line (1), it should pass through (-1, -1, -1) and is parallel to the line (1).Equation of the plane through (1) isa x+1+b y+1+c z+1 = 0 … 3,where 7a – 6b + c = 0 … 4Since the plane is parallel to the line (2),a-2b+c=0 … 5Solving (4) and (5) using cross-multiplication, we geta-4=b-6=c-8⇒a2=b3=c4Substituting a, b and c in (3), we get2 x+1+3 y+1+4 z+1=0⇒2x+3y+4z+9=0 … 6which is the equation of the plane containing line (1) and parallel to line (2).Shortest distance between (1) and (2)=Distance between the point P (3, 5, 7) and plane (6)=2 3+3 5+4 7+94+9+16=5829=2 29 units
Page 29.73 Ex. 29.15
Q1.
Answer :
Let Q be the image of the point P (0, 0, 0) in the plane 3x + 4y – 6z + 1 = 0 .Then, PQ is normal to the plane. So, the direction ratios of PQ are proportional to 3, 4, -6.Since PQ passes through P (0, 0, 0) and has direction ratios proportional to 3, 4 and -6, equation of PQ isx-03 = y-04 = z-0-6 = r (say)Let the coordiantes of Q be 3r, 4r, -6r. Let R be the mid-point of PQ. Then,R=0+3r2, 0+4r2, 0-6r2 = 3r2, 2r, -3rSince R lies in the plane 3x + 4y – 6z + 1 = 0,3 3r2 + 4 2r – 6 -3r + 1 = 0⇒r = -261Substituting this in the coordinates of Q, we getQ=3r, 4r, -6r = 3 -261, 4 -261, -6 -261 = -661, -861, 1261
Q2.
Answer :
Let Q be the image of the point P (1, 2, -1) in the plane 3x-5y+4z=5.Then PQ is normal to the plane. So, the direction ratios of PQ are proportional to 3, -5, 4.Since PQ passes through P (1, 2, -1) and has direction ratios proportional to 3, -5, 4, equation of PQ isx-13=y-2-5=z+14=r (say)Let the coordinates of Q be 3r+1, -5r+2, 4r-1. Let R be the mid-point of PQ. Then,R=3r + 1 + 12, -5r + 2 + 22, 4r – 1 – 12 = 3r + 22, -5r + 42, 4r – 22Since R lies in the plane 3x – 5y + 4z = 5,3 3r + 22 -5 -5r + 42 +4 4r – 22 = 5⇒9r + 6 + 25r – 20 + 16r – 8 = 10⇒50r – 32 = 0⇒r = 3250 = 1625Substituting the value of r in the coordinates of Q, we getQ=3r + 1, -5r + 2, 4r – 1 = 3 1625+1, -5 1625+2, 4 1625-1 = 7325, -65, 3925
Q3.
Answer :
Let M be the foot of the perpendicular of the point P (5, 4, 2) on the line x + 12 = y – 33 = z – 1-1Therefore, its equation isx + 12 = y – 33 = z – 1-1 = rThen, M is in the form 2r-1, 3r+3, -r+1Direction ratios of MP are 2r-1-5, 3r+3-4, -r+1-2 or 2r-6, 3r-1, -r-1.Since MP is perpendicular to the given line (2, 3, -1),2 2r-6+3 3r-1-1 -r-1=0 (Because a1a2+b1b2+c1c2=0)⇒4r-12+9r-3+r+1=0⇒14r-14=0⇒r=1So, M=2r-1, 3r+3, -r+1=2 1-1, 3 1+3, -1+1=1, 6, 0Length of the perperndicular, MP=1-52+6-42+0-22=16+4+4=24=2 6 units
Q4.
Answer :
Let Q be the image of the point P (3 i^+j^+2 k^) in the plane r.→ 2 i^-j^+ k^ = 4Since PQ passes through P and is normal to the given plane, it is parallel to the normal vector 2 i^-j^+k^. So, the equation of PQ isr→=3 i^+j^+2 k^+λ 2 i^-j^+k^As Q lies on PQ, let the position vector of Q be 3+2λ i^+1-λ j^+2+λ k^ .Let R be the mid-point of PQ. Then, the position vector of R is 3+2λ i^+1-λ j^+2+λ k^+3 i^+j^+2 k^2=6+2λ i^+2-λ j^+4+λ k^2=3+λ i^+1-λ2 j^+2+λ2 k^Since R lies in the plane r.→ 2 i^-j^+ k^ = 4,3+λ i^+1-λ2 j^+2+λ2 k^. 2 i^-j^+ k^ = 4⇒6+2λ-1+λ2+2+λ2=4⇒7 + 2λ + λ2 + λ2 = 4⇒ 14 + 6 λ = 8⇒ 6 λ = 8 – 14⇒ λ = -1Putting λ = -1 in Q, we get Q= 3+2(-1) i^+1-(-1) j^+2+(-1) k^ = i^ + 2 j^ +k ^or (1, 2, 1)Therefore, by putting λ = -1 in R, we get R = 3+(-1) i^+1-(-1)2 j^+2+(-1)2 k^= 2 i^ + 32 j^ +32 k^
Q5.
Answer :
Let M be the foot of the perpendicular of the point P (1, 1, 2) in the plane 2x – 2y + 4z + 5 = 0Then, PM is normal to the plane. So, the direction ratios of PM are proportional to 2, -2, 4.Since PM passes through P (1, 1, 2) and has direction ratios proportional to 2, -2 and 4, equation of PQ isx-12 = y-1-2 = z-24 = r (say)Let the coordiantes of M be 2r + 1, -2r + 1, 4r + 2.Since M lies in the plane 2x – 2y + 4z + 5 = 0,2 2r + 1 – 2 -2r + 1 + 4 4r + 2 + 5 =0⇒4r + 2 + 4r – 2 + 16r + 8 + 5 = 0⇒24r + 13 = 0⇒r = -13 24Substituting this in the coordinates of M, we getM=2r + 1, -2r + 1, 4r + 2 = 2 -13 24 + 1, -2 -13 24 + 1, 4 -13 24 + 2 = -1 12, 25 12, -16Now, the length of the perpendicular from P onto the given plane=2 1-2 1+4 2+54+4+16=1324 units
Q6.
Answer :
The given plane is x − y + z = 5. We need to find the distance of the point from the point(1, -2, 3) measured along a parallel line x2=y3=z-6.
Let the line from point be P(1, -2, 3) and meet the plane at point Q.
Direction ratios of the line from the point (1, -2, 3) to the given plane will be the same as the given line x2=y3=z-6.
So the equation of the line passing through P and with same direction ratios will be:
x-12 = y+23 = z-3-6 = λ⇒x = 2λ + 1, y = 3λ-2, z = -6λ+3
coordinates of any point on the line PQ are x = 2λ + 1, y = 3λ-2, z = -6λ+3.
Now, since Q lies on the plane so it must satisfy the equation of the plane.
that is, x − y + z = 5
therefore, 2λ+1 – (3λ – 2) + (-6λ +3) = 5
λ = 17
coordinates of Q are (27+1), (37-2), (-67+3) = 97, -117, 157
using distance formula we have the length of PQ as
PQ = 97-12 + -117+22 + 157-32 =272 + 372 + -672 =449 + 949 + 3649 =4949 = 1
Hence PQ = 1
So, the distance of the point (1, −2, 3) from the plane x − y + z = 5 is 1
Q7.
Answer :
Let M be the foot of the perpendicular of the point P (2, 3, 7) in the plane 3x – y – z = 7.Then, PM is normal to the plane. So, the direction ratios of PM are proportional to 3, -1, -1.Since PM passes through P (2, 3, 7) and has direction ratios proportional to 3, -1 and -1, equation of PQ isx-23 = y-3-1 = z-7-1 = r (say)Let the coordinates of M be 3r + 2, -r + 3, -r + 7.Since M lies in the plane 3x – y – z = 7,3 3r + 2 – -r + 3 – -r + 7 = 7⇒9r + 6 + r – 3 + r – 7 = 7⇒11r = 11⇒r = 1Substituting this in the coordinates of M, we getM = 3r + 2, -r + 3, -r + 7 = 3 1 + 2, -1 + 3, -1 + 7 = 5, 2, 6Now, the length of the perpendicular from P onto the given plane=3 2-3-7-79+1+1=1111=11 units
Q8.
Answer :
Let Q be the image of the point P (1, 3, 4) in the plane 2x-y+z+3=0.Then PQ is normal to the plane. So, the direction ratios of PQ are proportional to 2, -1, 1.Since PQ passes through P (1, 3, 4) and has direction ratios proportional to 2, -1 and 1, equation of PQ isx-12=y-3-1=z-41=r (say)Let the coordinates of Q be 2r+1, -r+3, r+4. Let R be the mid-point of PQ. Then,R=2r+1+12, -r+3+32, r+4+42=r+1, -r+62, r+82Since R lies in the plane 2x – y + z + 3 = 0,2 r+1 – -r+62 + r+82 + 3 = 0⇒4r + 4 + r – 6 + r + 8 + 6 = 0⇒6r + 12 = 0⇒r = -2Substituting this in the coordinates of Q, we getQ=2r+1, -r+3, r+4.=2 -2+1, 2+3, -2+4=-3, 5, 2
Q9.
Answer :
The given equation of the line isr→=2 i^-j^+2 k^+λ 3 i^+4 j^+2 k^⇒r→=2+3λ i^+-1+4λ j^+2+2λ k^The coordinates of any point on this line are of the form 2+3λ i^+-1+4λ j^+2+2λ k^ or 2+3λ, -1+4λ, 2+2λSince this point lies on the plane r→. i^-j^+k^ = 5, 2+3λ i^+-1+4λ j^+2+2λ k^. i^-j^+k^=5⇒2+3λ+1-4λ+2+2λ-5=0⇒λ=0So, the coordinates of the point are2 + 3λ, -1 + 4λ, 2 + 2λ=2 + 0, -1 + 0, 2 + 0=2, -1, 2The coordinates of the point corresponding to the position vector -i^-5 j^-10 k^ are (-1, -5, -10).Distance between (2, -1, 2) and (-1, -5, -10)=-1-22+-5+12+-10-22=9+16+144=13 units
Q10.
Answer :
Let M be the foot of the perpendicular of the point P (1, 1, 2) in the plane r→. i^ – 2 j^+ 4 k^ + 5 = 0 or x-2y + 4z + 5 = 0.Then, PM is the normal to the plane. So, the direction ratios of PM are proportional to 1, -2, 4.Since PM passes through P (1, 1, 2) and has direction ratios proportional to 1,-2, 4 equation of PQ isx-11 = y-1-2 = z-24 = r (say)Let the coordinates of M be r+1, -2r+1, 4r+2.Since M lies in the plane x – 2y + 4z + 5 = 0,x – 2y + 4z + 5 = 0⇒r + 1 + 4r – 2 + 16r + 8 + 5 = 0⇒21r + 12 = 0⇒r=-1221=-47Substituting this in the coordinates of M, we getM=r+1, -2r+1, 4r+2= -47+1, -2 -47+1, 4 -47+2 = 37, 157,-27 Now, the length of the perpendicular from P onto the given plane= 1-2 1+4 2+51+4+16=1221 units
Page 29.74 Ex. 29.15
Q11.
Answer :
Let M be the foot of the perpendicular of the point P (3, 2, 1) in the plane 2x – y + z + 1 = 0.Then, PM is the normal to the plane. So, the direction ratios of PM are proportional to 2, -1, 1.Since PM passes through P (3, 2, 1) and has direction ratios proportional to 2, -1, 1,equation of PQ isx-32=y-2-1=z-11=r (say)Let the coordinates of M be 2r+3, -r+2, r+1.Since M lies in the plane 2x-y+z+1=0,2 2r + 3 – -r + 2 + r + 1 + 1 = 0⇒4r + 6 + r – 2 + r + 2 = 0⇒6r=-6⇒r=-1Substituting the value of r in the coordinates of M, we getM=2r + 3, -r + 2, r + 1 = 2 -1 + 3, –1 + 2, -1 + 1 = 1, 3, 0Now, the length of the perpendicular from P onto the given plane=2 3 – 2 + 1 + 14 + 1 + 1= 66=6 units
Q12.
Answer :
For the unit vector perpendicular to the given plane, we need to convert the given equation of plane into normal form.
The given equation of the plane isr→. 6 i^ – 3 j^ – 2 k^ + 1 = 0⇒r→. 6 i^ – 3 j^ – 2 k^ = -1⇒r→. -6 i^ + 3 j^ + 2 k^ = 1 … 1Now, -62 + 32 + 22 = 36 + 9 + 4 = 7Dividing (1) by 7, we getr→. -67 i^ + 37 j^ + 27 k^ = 17, which is in the normal form r→. n →= d,where the unit vector normal to the given plane, n →= -67 i^ + 37 j^ + 27 k^So, its direction cosines are -67, 37, 27
Q14.
Answer :
Let M be the foot of the perpendicular of the origin P (0, 0, 0) in the plane 2x-3y+4z-6=0.Then, PM is normal to the plane. So, the direction ratios of PM are proportional to 2, -3, 4.Since PM passes through P (0, 0, 0) and has direction ratios proportional to 2, -3, 4, the equation of PQ isx-02=y-0-3=z-04=r (say)Let the coordiantes of M be 2r, -3r, 4r.Since M lies in the plane 2x – 3y + 4z – 6 = 0,2 2r – 3 -3r + 4 4r – 6 = 0⇒4r + 9r + 16r – 6 = 0⇒29r – 6 = 0⇒r = 629Substituting the value of r in the coordinates of M, we getM=2r, -3r, 4r=2 629, -3 629, 4 629=1229, -1829, 2429
Page 29.75 (Very Short Answers)
Q1.
Answer :
The equation of the plane parallel to the plane XOY is z=b … 1, where b is a constant.It is given that this plane passes through (2,-3, 5). So,5=bSubstituting this value in (1), we get z=5, which is the required equation of the plane.
Q2.
Answer :
The equation of the plane parallel to the plane YOZ is x = b … 1, where b is a constant.It is given that this plane passes through (-4, 1, 0). So,-4 = bSubstituting this value in (1), we get x=-4 , which is the required equation of the plane.
Q3.
Answer :
The equation of the plane passing through (a, 0, 0), (0, b, 0) and (0, 0, c) is
x-ay-0z-00-ab-00-00-a0-0c-0 = 0 ⇒x-ay z-ab0-a0c =0⇒bc x-a + acy + abz = 0⇒bcx + acy + abz = abcDividing the equation by abc, we getxa + yb + zc = 1
Q4.
Answer :
The general equation of a plane isax + by + cz + d = 0 … 1This plane is parallel to the x – axis.It means that this plane passes through the point 0, y, z. So,a 0 + by + cz + d = 0⇒by + cz + d = 0
Q5.
Answer :
We know that the planes a1x + b1y + c1z + d1 = 0 and a2x + b2y + c2z + d2 = 0 are perpendicular to each other only if a1a2 + b1b2 + c1c2 = 0The given planes are x – 2y + kz = 4 and 2x + 5y – z = 9⇒a1 = 1; b1 = -2; c1 = k; a2 = 2; b2 = 5; c2 = -1It is given that the given planes are perpendicular. ⇒a1a2 + b1b2 + c1c2 = 0⇒1 2 + -2 5 + k -1 = 0⇒2 – 10 – k = 0⇒-8 – k = 0⇒k = -8
Q6.
Answer :
The given equation of the plane is2x – 3y + 4z = 12Dividng both sides by 12, we get⇒2×12 + -3y12 + 4z12 = 1212⇒x6 + y-4 + z3 = 1 … 1We know that the equation of the plane whose intercepts on the coordianate axes are a, b and c isxa + yb + zc = 1 … 2Comparing (1) and (2), we geta= 6, b =-4 and c = 3
Q7.
Answer :
We know that the ratio in which the plane ax+by+cz+d=0 divides the line segment joining x1, y1, z1 and x2, y2, z2 is- ax1+by1+cz1+dax2+by2+cz2+dHere, a = 4; b = 5; c = -3; d = -8; x1 = -2; y1 = 1; z1 = 5; x2 = 3; y2 = 3; z2 = 2So, the required ratio=- 4 -2+5 1-3 5-84 3+5 3-3 2-8=- -8+5-15-812+15-6-8=2613=21 or 2 : 1
Q8.
Answer :
The given equations are 2x – y + 3z = 4 … 1The second equation of the plane is2x – y + 3z = 18 … 2We know that the distance between two planes ax + by + cz = d1 and ax + by + cz = d2 is d2-d1a2+b2+c2So, the required distance is 18-422+-12+32=144+1+9=1414=14 units
Q9.
Answer :
The given equation of the plane isr→. 2 i^+3 j^-6 k^ = 14 or r→. n→ =14, where n→ = 2 i^ + 3 j^ – 6 k^n→=4+9+36=7For reducing the given equation to normal form, we need to divide it by n→. Then, we getr→. n→n→=14n→⇒r→. 2 i ^+ 3 j^ – 6 k^7 = 147⇒r→. 27 i^ + 37 j^ – 67k^ = 2, which is the required normal form.
Q10.
Answer :
The given equation of the plane isr→. 2 i^- j^+2 k^ = 12 or r→. n→ = -6, where n→ = 2 i ^- j^ + 2 k^n→ = 4+1+4 = 3For reducing the given equation to normal form, we need to divide both sides by n→. Then, we getr→. n→n→=12n→⇒r→. 2 i^- j^+2 k^3 = 123⇒r→. 23 i^-13 j^+23k^ = 4 … 1The equation of the plane in normal form isr→. n^ = d … 2(where d is the distance of the plane from the origin)Comparing (1) and (2),length of the perpendicular from the origin to the plane = d = 4 units
Q11.
Answer :
The equation of the given plane isr→= a→ + λ b→ + μ c→So, the plane passes through the vector a→ and parallel to the vectors b→ and c→.So, the plane passes through the vector a→ whose normal vector is b→ × a→ (It means that n→=b→×a→)So, the equation of the plane in scalar product form isr→-a→. n→=0⇒r→-a→. b→×c→=0
Q12.
Answer :
The equation of the given plane isr→=l b→+m c→So, the plane passes parallel to the vectors b→ and c→.So, the vector normal to the plane is b→ × c→.
Q13.
Answer :
Let the equation of a plane parallel to the given plane be 3x+2y-z=k … 1This passes through (2, -1, 1). So, 3 2+2 -1-1=k⇒k=3Substituting this in (1), we get3x+2y-z=3, which is the equation of the required plane.
Q14.
Answer :
The given plane passes through the linesr→=a→+λ b→ and r→=a→+μ c→So, the plane passes through the vector a→ and parallel to the vectors b→ and c→.So, the plane passes through the vector a→ whose normal vector is b→ × a→. (It means that n→=b→×a→)So, the equation of plane in scalar product form isr→-a→. n→=0⇒r→-a→. b→×c→=0
Q15.
Answer :
Given equation of the line isr →=a → + λ b→… 1Given equation of the plane isr→. n→ = 0⇒a→ + λ b→. n →= 0 [From (1)]⇒a→. n→ + λ b→. n→ = 0⇒λ = -a→. n→b→. n→Substituting this in (1), we getr→=a→-a→. n→b→. n→ b→, which is the required position vector that lies both on the line and the plane.
Q16.
Answer :
Direction ratios of the given line x-12 = y-13 = z-1k are proportional to 2, 3, k.Direction ratios of the normal to the plane r→. 2 i ^+ 3 j^ + 4 k^ = 4 are 2, 3, 4.Given that these two are perpendicular.⇒2 2+3 3 + k4 = 0 (Because a1a2 + b1b2 + c1c2 = 0)⇒4 + 9 + 4k =0⇒13 + 4k = 0⇒k = -134
Q17.
Answer :
The given line is parallel to the vector b→=i^ + 2 j^ + 2 k^ and the given plane is normal to the vector n→=i^ + j^+0 k^.We know that the angle θ between the line and the plane is given bysin θ=b→. n→b→ n→=i^ + 2 j^ + 2 k^. i ^+ j ^+ 0 k^i^ + 2 j^ + 2 k^ i^ + j^ + 0 k^=1 + 2 + 01 + 4 + 4 1 + 1 + 0 = 33 2 = 12⇒θ = sin-1 12 = 45o
Q18.
Answer :
For x- interecept, put y = 0 and z = 0 in the given equation. Then, we get2x+0-0=5⇒2x=5⇒x=52
Q19.
Answer :
We know that the distance of the point x1, y1, z1 from the plane ax + by + cz + d = 0 is given byax1 + by1 + cz1 + da2 + b2 + c2So, the required distance =2 0-3 0+6 0+2122 + -32 + 62=214 + 9 + 36=217=3 units
Q20.
Answer :
The required line is normal to the plane r→.2 i^+j^+2 k^=5 and it is parallel to the normal vector of the plane.So, the required line is parallel to the vector b→=2 i^+j^+2 k^It is given that the line passes through the point (1, -2, -3) whose position vector is given by a→=i^-2 j^-3 k^.We know that the equation of the line passing through the point whose position vector is a→ and parallel to the vector b→ is given byr→=a→+λ b→⇒r→=i^ – 2 j^ – 3 k^ + λ 2 i^ + j^ + 2 k^
Page 29.76 (Multiple Choice Questions)
Q1.
Answer :
(a) 2x − y = 0 and y − 3z = 0
The given plane is2x – 1 + λ y + 3λz = 0⇒2x – y + λ -y + 3z = 0So, this plane passes through the intersection of the planes2x – y = 0 and -y + 3z = 0⇒2x – y = 0 and y – 3z = 0
Q2.
Answer :
(b) 60°
We know that the angle between the planes a1x + b1y + c1z + d1 = 0 and a2x + b2y + c2z + d2 = 0 is given bycos θ=a1a2 + b1b2 + c1c2a12 + b12 + c12 a22 + b22 + c22So, the angle between 2x – y + z = 6 and x + y + 2z = 3 is given bySo, cos θ =2 1 + -1 1 + 1 222 + -12 + 12 12 + 12 + 22 = 2 – 1 + 24 + 1 + 1 1 + 1 + 4 = 36 6 = 36 = 12⇒θ = cos-112 = 60o
Q3.
Answer :
(c) 51x − 15y − 50z + 173 = 0
The equation of the plane passing through the line of intersection of the given planes isx + 2y + 3z – 4 + λ 2x + y – z + 5 = 0 1 + 2λx + 2 + λy + 3 – λz – 4 + 5λ = 0… 1This plane is perpendicular to 5x + 3y + 6z + 8 = 0. So,5 1 + 2λ + 32 + λ + 6 3 – λ = 0 (Because a1a2 + b1b2 + c1c2 = 0)⇒5 + 10λ + 6 + 3λ + 18 – 6λ = 0⇒7λ + 29 = 0⇒λ = – 29 7Substituting this in (1), we get1 + 2 – 297x + 2 + – 297y + 3 + 297z – 4 + 5 – 29 7 = 0⇒ 51x +15y – 50z +173 = 0
Q4.
Answer :
(c) 16
Multiplying the first equation of the plane by4x+4y-2z+4=0 4x+4y-2z=-4 … 1The second equation of the plane is4x+4y-2z+5=04x+4y-2z=-5 … 2We know that the distance between two planes ax+by+cz=d1 and ax+by+cz=d2 is d2-d1a2+b2+c2So, the required distance = -5+442+42+-22=-116+16+4=136=16 units
Q5.
Answer :
(b) (−3, 5, 2)
Let Q be the image of the point P (1, 3, 4) in the plane 2x-y+z+3=0Then PQ is normal to the plane. So, the direction ratios of PQ are proportional to 2, -1, 1.Since PQ passes through P (1, 3, 4) and has the direction ratios proportional to 2, -1, 1., equation of PQ isx-12=y-3-1=z-41=r (say)Let the coordinates of Q be 2r+1, -r+3, r+4. Let R be the mid point of PQ. Then,R=2r+1+12, -r+3+32, r+4+42=r+1, -r+62, r+82Since R lies in the plane 2x-y+z+3=0,2 r+1–r+62+r+82+3=0⇒4r+4+r-6+r+8+6=0⇒6r+12=0⇒r=-2Substituting this in the coordinates of Q, we getQ=2r+1, -r+3, r+4.=2 -2+1, 2+3, -2+4=-3, 5, 2
So, the answer is (b).
Q6.
Answer :
(d) None of these
x−12=y+1−1=z−03 and x−2=y−2−3=z+1−1
Now, if these two lines lie on a plane, so the direction ratio of lines will be perpendicular to the plane’s normal vector.
Q7.
Answer :
(a) r→·5i^-2j^-3k^=7
We know that the equation r→=a→+λb→+μc→ represents a plane passing through a point whose position vector is a→ and parallel to the vectors b→ and c→.Here, a→ = i^- j^ + 0 k^; b→ = i^+j^+k^; c→ = i^-2 j^+3 k^Normal vector, n→=b→×c→=i^j^k^1111-23=5 i^-2 j^-3 k^The vector equation of the plane in scalar product form isr→. n→=a→. n→⇒r→. 5 i^-2 j^-3 k^=i^ – j^ + 0 k^. 5 i^ – 2 j^ – 3 k^⇒r→. 5 i^ – 2 j^ – 3 k^ = 5 + 2 + 0⇒r→. 5 i^ – 2 j^ – 3 k^ = 7⇒r→. 5 i^ – 2 j^ – 3 k^ = 7
Q8.
Answer :
(b) 1033
The given line passes through the point whose position vector is a→=2 i^-2 j^+3 k^.We know that the perpendicular distance of a point P of position vector a→ from the plane r→. n→ = d is given by p=a→. n→-dn→Here,a→=2 i^-2 j^+3 k^; n→=i^+5 j^+k^; d=5So, the required distance p is given byp=2 i^-2 j^+3 k^. i^+5 j^+k^-5i^+5 j^+k^=2-10+3-51+25+1=-1027=103 3 units
Q9.
Answer :
(a) x − 5y + 3z = 7
The equation of the plane passing through the line of intersection of the given planes isx + y + z + 3 + λ 2x – y + 3z + 1 = 0 1 + 2λx + 1 – λy + 1+ 3λz + 3 + λ = 0… 1This plane is parallel to the line x1 = y2 = z3. It means that this line is perpendicular to the normal of the plane (1).⇒1 1 + 2λ + 2 1 -λ + 3 1 + 3λ=0 (Because a1a2 + b1b2 + c1c2 = 0)⇒1 + 2λ + 2 – 2λ + 3 + 9λ = 0⇒9λ+6=0⇒λ=-23Substituting this in (1), we get1+2 -23x+1–23y+1+3 -23z+3+-23=0⇒-x+5y-3z+7=0⇒x-5y+3z=7
Page 29.77 (Multiple Choice Questions)
Q10.
Answer :
(a) r→·i^+3k^=10
Let the direction ratios of the required plane be proportional to a, b, c.Since the required plane contains the line r→= -2 i^-3 j^+4 k^+λ 3 i^-2 j^-k^, it must pass through the point (-2, -3, 4) and it should be parallel to the line.So, the equation of the plane is a x + 2 + b y + 3 + c z – 4 = 0 … 1 and3a – 2b – c = 0 … 2It is given that plane (1) passes through the point i^ + 2 j^ + 3 k^ or (1, 2, 3). So,a 1 + 2 + b 2 + 3 + c 3 – 4 = 0 3a+5b-c=0 … 3Solving (1), (2) and (3), we getx+2y+3z-43-2-135-1=0⇒7 x+2+0 y+3+21 z-4=0⇒x + 2 + 3z – 12=0⇒x + 3z = 10 or r→. i^ +3 k^ = 10
Q11.
Answer :
(c) 3
Let α, β and γ be the intercepts of the given plane on the coordinate axes.Then, the plane meets the coordinate axes atA α, 0, 0, B 0, β, 0 and C=0, 0, γGiven that the centroid of the triangle = a, b, c⇒α + 0 + 03, 0 + β + 03, 0 + 0 + γ3 = a, b, c⇒α3, β3, γ3 = a, b, c⇒α3 = a, β3 = b, γ3 = c⇒α = 3a, β = 3b, γ = 3c … 1Equation of the plane whose intercepts on the coordinate axes are α, β and γ isxα + yβ + zγ = 1⇒x3a + y3b + z3c = 1 [From (1)]⇒xa + yb + zc = 3
Q12.
Answer :
(c) 3
The coordinates of any point on the given line are of the formx-31=y-42=z-52=λ⇒x = λ + 3; y = 2λ + 4; z = 2λ + 5So, the coordiantes of the point on the given line are λ+3, 2λ+4, 2λ+5. This point lies on the plane, x + y + z = 17⇒λ + 3 + 2λ + 4 + 2λ + 5 = 17 ⇒5λ = 5⇒λ = 1So, the coordinates of the point areλ+3, 2λ+4, 2λ+5=1+3, 2 1+4, 2 1+5=4, 6, 7Now, the distance between the points 4, 6, 7 and 3, 4, 5 is3-42+4-62+5-72=1+4+4=3 units
So, the answer is (c).
Q13.
Answer :
(b) 2i^+7j^-13k^
Let the required vector be a i^ + b j^ + c k^ … 1Since the vector is parallel to the line of intersection of the given planes, 3a – b + c = 0 … 2a + 4b – 2c = 0 … 3Solving (2) and (3), we get a-2 = b7 = c13Substituting these values in (1), we get-2 i^ + 7 j^ + 13 k^, which is the required vector.
Q14.
Answer :
(c) 7/5
Since the plane is perpendicular to the given line, its direction ratios are proportional to 3, 0, 4So, the required equation of the plane is of the form3x + 0y + 4z + d = 0… 1, where d is a constant.Since this plane passes through (1, 1, 1),3 + 0 + 4 + d = 0⇒d =-7Substituting this in (1), we get3x + 0y + 4z – 7 = 0 … 2Perpendicular distance of (2) from the origin=3 0 + 0 + 4 0 – 732 + 02 + 42=0 + 0 – 725=75 units
Q15.
Answer :
a) x − 4y + 2z + 4 = 0
Let a, b, c be the direction ratios of the required plane.The given line equations can be rewritten asx-11 = y-5212 = z-012 … 1x-0 13 = y-11414 = z-4313 … 2Since the required plane is parallel to the lines (1) and (2),a + b2 + c2 = 0 ⇒2a + b + c = 0 … 3a3 + b4 + c3 = 0 ⇒4a + 3b + 4c = 0 … 4Solving (3) and (4) using cross-multiplication method, we geta1 = b-4 = c2 = λ (say)⇒a = λ, b = -4λ, c = 2λNow, the equation of the plane whose direction ratios are λ, -4λ, 2λ and passing through the point (2, 3, 3) isλ x – 2 + -4λy – 3 + 2λ z – 3 = 0⇒x – 4y + 2z + 4 = 0
So, the answer is (a).
Q16.
Answer :
(b) 13
Given equation of line isr →= 2 i^ – j ^+ 2 k^ + λ 3 i^ + 4 j ^+ 12 k^⇒r→ = 2 + 3λ i^ + -1 + 4λ j ^+ 2 + 12λ k^The coordinates of any point on this line are of the form 2 + 3λ i^ + -1 + 4λ j ^+ 2 + 12λ k^. or 2 + 3λ, -1 + 4λ, 2 + 12λSince this point lies on the plane r→. i^ – j^ + k^ = 5 ,2 + 3λ i^ + -1 + 4λ j^ + 2 + 12λ k^. i^ – j^ + k^ = 5 ⇒2 + 3λ + 1 – 4λ + 2 + 12λ – 5 = 0⇒λ = 0So, the coordinates of the point are 2 + 3λ, -1 + 4λ, 2 + 2λ=2 + 0, -1 + 0, 2 + 0=2, -1, 2Distance between (2, -1, 2) and (-1, -5, -10)=-1 -22 + -5 + 12 + -10 – 22=9 +16+144=13 units
Q17.
Answer :
The equation of the plane passing through the intersection of the planes
ax + by + cz + d = 0
and lx + my + nz + p = 0
will be (ax + by + cz + d) + λ(lx + my + nz + p) = 0
x(a + λl) + y(b + λm) + z(c + λn) + (d + λp)=0 …….(1)
Since the plane is parallel to the line y=0 and z=0
a + λl=0
λ = -al
putting the value of λ in equation (1), we get
x(a + (-al)l) + y(b + (-al)m) + z(c + (-al) n) + d + (-al)p =0
y(bl – am) + z(cl -an) + dl – ap =0
Hence, option (a)
Q18.
Answer :
(a) x + y + z = 1
We know that the equation of aplane whose intercepts are a, b, c isxa+yb+zc=1 … 1It is given that a = b = cSo, from (1),xa + ya + zc = 1 ⇒x + y + z = a … (2)Since it is given that the intercepts of the required plane are of unit length,a = b = c = 1Substituting a = 1 in (2), we getx + y + z = 1
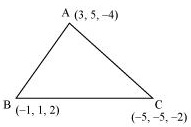
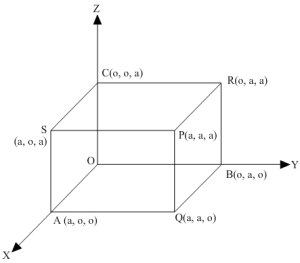
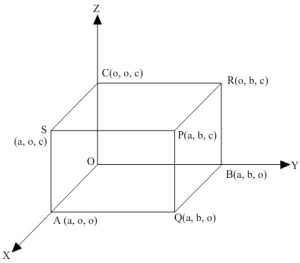
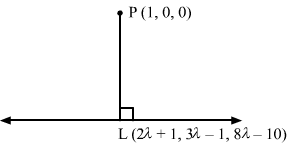
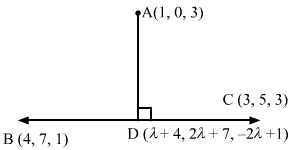
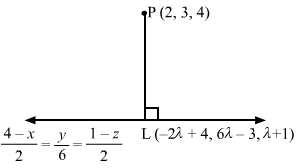
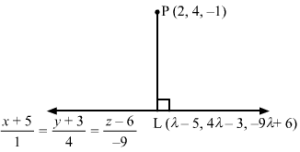
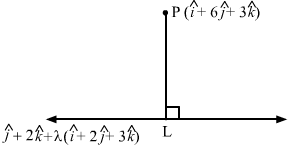
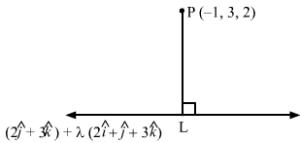
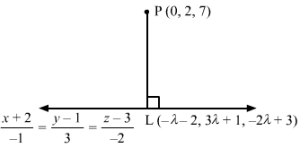
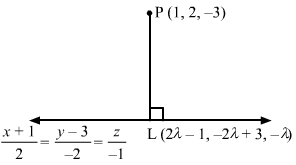
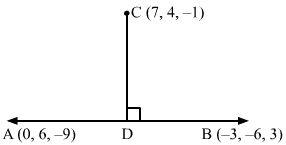

Leave a Reply