Notes For All Chapters – गणित प्रकाश Class 6th
परिमाप और क्षेत्रफल
1. परिमाप (Perimeter) क्या होता है?
परिमाप किसी बंद आकृति की बाहरी सीमा की कुल लंबाई होती है।
सरल शब्दों में — किसी आकृति के चारों ओर एक बार घूमने पर जितनी दूरी तय होती है, वही उसका परिमाप होता है।
2. विभिन्न आकृतियों के परिमाप के सूत्र:
● आयत (Rectangle) का परिमाप:
सूत्र: 2 × (लंबाई + चौड़ाई)
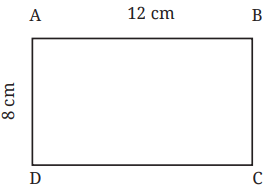
उदाहरण: यदि लंबाई = 12 सेमी, चौड़ाई = 8 सेमी → परिमाप = 2 × (12 + 8) = 40 सेमी
● वर्ग (Square) का परिमाप:
सूत्र: 4 × भुजा की लंबाई (a)
उदाहरण: भुजा = 1 मीटर → परिमाप = 4 × 1 = 4 मीटर
● त्रिभुज (Triangle) का परिमाप:
सूत्र: तीनों भुजाओं की लंबाई का योग
उदाहरण: भुजाएँ = 4 सेमी, 5 सेमी, 7 सेमी → परिमाप
(a + b + c) = (4+5+7) = 16 सेमी
● समभुज त्रिभुज (Equilateral Triangle) का परिमाप:
सूत्र: 3 × भुजा की लंबाई
3. परिमाप से जुड़े वास्तविक जीवन के प्रश्न:
मेज़पोश, पार्क, टेप, रस्सी इत्यादि की कुल लंबाई निकालने में परिमाप का प्रयोग होता है।
4. क्षेत्रफल (Area) क्या होता है?
किसी बंद आकृति के अंदर के भाग को घेरने वाला क्षेत्र ही उसका क्षेत्रफल होता है।
क्षेत्रफल हमेशा वर्ग इकाइयों (जैसे वर्ग सेमी, वर्ग मीटर) में मापा जाता है।
5. विभिन्न आकृतियों के क्षेत्रफल के सूत्र:
● आयत (Rectangle) का क्षेत्रफल:
सूत्र: लंबाई × चौड़ाई
● वर्ग (Square) का क्षेत्रफल:
सूत्र: भुजा × भुजा(a) = या भुजा²
● समभुज त्रिभुज (Equilateral Triangle):
सूत्र: 3 × भुजा (परिमाप के लिए), लेकिन क्षेत्रफल के लिए ग्रिड पेपर या विभाजन का उपयोग करें
6. ग्राफ पेपर से क्षेत्रफल मापन:
पूरा भरा हुआ वर्ग = 1 वर्ग इकाई
आधा भरा हुआ = ½ इकाई
आधे से कम = 0 इकाई
आधे से अधिक = 1 इकाई
7. नियमित बहुभुज (Regular Polygon):
जिन आकृतियों के सभी भुजाएँ और कोण बराबर हों।
जैसे — समभुज त्रिभुज, नियमित पंचभुज, वर्ग आदि।
परिमाप = एक भुजा की लंबाई × भुजाओं की संख्या
8. त्रिभुज का क्षेत्रफल (Area of Triangle):
किसी वर्ग या आयत को तिरछा काटकर दो बराबर त्रिभुज बनाए जा सकते हैं।
क्षेत्रफल = आयत/वर्ग के क्षेत्रफल का आधा
9. महत्वपूर्ण अवधारणाएँ:
एक जैसे क्षेत्रफल वाली दो आकृतियों के परिमाप अलग हो सकते हैं।
एक जैसे परिमाप वाली आकृतियों के क्षेत्रफल अलग हो सकते हैं।
आकृति जितनी फैली हुई होगी, उसका परिमाप उतना अधिक होगा।







Leave a Reply