Question Answer For All Chapters – गणित प्रकाश Class 6th
शून्य के दूसरी ओर
आइए, पता लगाएँ (Page – 245)
1. +2 तल से प्रारंभ कीजिए और लिफ्ट में -3 दबाइए । आप कहाँ पहुँचेंगे? इसे पद के रूप में दर्शाइए।
उत्तर: आप –1 तल पर पहुँचेंगे।
पद (expression) के रूप में:
(+2) + (–3) = –1
व्याख्या:
+2 तल से नीचे की ओर 3 तल जाने का अर्थ है –3 जोड़ना।
इसलिए:
(+2) + (–3) = –1
2. दिए गए पदों को पूर्ण कीजिए। (आप प्रारंभ तल + मजेदार इमारत में गति के संदर्भ को ध्यान रखते हुए इन्हें पूर्ण कीजिए।)
(a) (+ 1) + (+ 4 ) = ___________
(b) (+ 4) + (+ 1) = ___________
(c) (+ 4) + (- 3) = ___________
(d) (- 1) + (+ 2) = ___________
(e) (- 1) + (+ 1) = ___________
(f) 0 + (+ 2) = ___________
(g) 0 + (- 2) = ___________
उत्तर: (a) (+1) + (+4) = +5
प्रारंभ +1 से 4 तल ऊपर जाएँगे = +5
(b) (+4) + (+1) = +5
+4 से 1 तल ऊपर जाएँगे = +5
(c) (+4) + (–3) = +1
+4 से 3 तल नीचे जाएँगे = +1
(d) (–1) + (+2) = +1
–1 से 2 तल ऊपर जाएँगे = +1
(e) (–1) + (+1) = 0
–1 से 1 तल ऊपर जाएँगे = 0 (भूमि तल)
(f) 0 + (+2) = +2
भूमि तल से 2 तल ऊपर = +2
(g) 0 + (–2) = –2
भूमि तल से 2 तल नीचे = –2
3. विभिन्न तलों से शुरुआत करते हुए, तल (-5) पर पहुँचने के लिए आवश्यक गतियों को ज्ञात कीजिए । उदाहरण के लिए, यदि मैं तल +2 से प्रारंभ करता हूँ, मुझे -5 पर पहुँचने के लिए -7 ही दबाना होगा। अतः अभिव्यक्ति (+ 2) + (-7) – 5 है।
इसी प्रकार -5 पर पहुँचने के लिए अन्य प्रारंभिक स्थितियाँ और आवश्यक गतियों को ज्ञात कीजिए और पदों को लिखिए।
उत्तर: i) प्रारंभ तल = +1
पद: (+1) + (–6) = –5
ii) प्रारंभ तल = +3
पद: (+3) + (–8) = –5
iii) प्रारंभ तल = +4
पद: (+4) + (–9) = –5
आइए, पता लगाएँ (Page 245 – 246)
संयोजित बटन दबाने से गति के परिणामों को ध्यान में रखते हुए दिए गए पदों का मूल्यांकन कीजिए।
(a) (+ 1) + (+ 4) = ____________
(b) (+ 4) + (+ 1) = ____________
(c) (+ 4) + (- 3) + (- 2) = ____________
(d) (- 1) + ( + 2) + (- 3) = ____________
उत्तर: (a) (+1) + (+4) = +5
1 तल ऊपर + 4 तल ऊपर = कुल 5 तल ऊपर
(b) (+4) + (+1) = +5
4 तल ऊपर + 1 तल ऊपर = कुल 5 तल ऊपर
(c) (+4) + (–3) + (–2) = –1
4 तल ऊपर – 3 तल नीचे – 2 तल नीचे = कुल 1 तल नीचे
(d) (–1) + (+2) + (–3) = –2
1 तल नीचे + 2 तल ऊपर – 3 तल नीचे = कुल 2 तल नीचे
आइए, पता लगाएँ (Page 247)
1. मजेदार इमारत का प्रयोग करते हुए दी गई संख्याओं की तुलना कीजिए और बॉक्स में < या > चिह्न भरिए।
a. –2 ☐ +5
उत्तर: –2 < +5
b. –5 ☐ +4
उत्तर: –5 < +4
c. –5 ☐ –3
उत्तर: –5 < –3
(क्योंकि –5 और –3 दोनों नकारात्मक हैं, पर –5 और नीचे है।)
d. +6 ☐ –6
उत्तर: +6 > –6
e. 0 ☐ –4
उत्तर: 0 > –4
f. 0 ☐ +4
उत्तर: 0 < +4
2. मजेदार इमारत में अधिक तलों की कल्पना कीजिए तथा संख्याओं की तुलना कीजिए। बॉक्स में < या > भरिए-
a. –10 ☐ –12
उत्तर: –10 > –12
(क्योंकि –10, –12 से ऊपर होता है।)
b. +17 ☐ –10
उत्तर: +17 > –10
(धनात्मक संख्या हमेशा ऋणात्मक संख्या से बड़ी होती है।)
c. 0 ☐ –20
उत्तर: 0 > –20
d. +9 ☐ –9
उत्तर: +9 > –9
e. –25 ☐ –7
उत्तर: –25 < –7
(–25 बहुत नीचे होता है।)
f. +15 ☐ –17
उत्तर: +15 > –17
3. यहाँ दाईं ओर एक रेखा के रूप में दिखाई गई इमारत में यदि तल A = -12, तल D = -1 और तल E = + 1 है, तो तल B, C, F, G और H के क्रमांक बताइए।
उत्तर: आइए हम रेखा पर संख्याएँ चिह्नित करें:
0, –1, –2, –3, …………, –12 और 1, 2, 3, ……….., 12
अब प्रत्येक तल को गिनने पर हमें निम्नलिखित परिणाम मिलते हैं:
B = –9, C = –6, F = +2, G = +6, H = +11
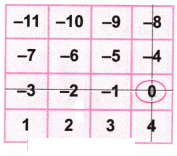
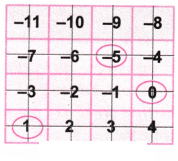
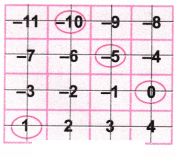
4. यहाँ दाईं ओर दिखाई गई इमारत में निम्नलिखित तलों को अंकित कीजिए।
(a) -7
(b) -4
(c) +3
(d) -10
उत्तर: यहाँ, एक रेखा को एक तल माना गया है।
तल 0 से ऊपर के तल को धनात्मक संख्याओं से और 0 से नीचे के तल को ऋणात्मक संख्याओं से चिह्नित किया गया है।
अब आइए तल पर घेरा बनाकर इमारत में निम्नलिखित संख्याओं ( -7, 4, 3, 10) को अंकित करें।
आइए, पता लगाएँ (Page 249)
1. दिए गए पदों को पूरा कीजिए। आप इन्हें प्रारंभिक तल से लक्षित तल तक पहुँचने के लिए आवश्यक गति प्राप्त करने के रूप में सोच सकते हैं।
(a) (+ 1) – (+ 4) = ____________
(b) (0) – (+ 2) = ____________
(c) (+ 4) – (+ 1) = ____________
(d) (0) – (- 2) = ____________
(e) (+ 4) – (- 3)= ____________
(f) (4) – (- 3) = ____________
(g) (- 1) – (+ 2) = ____________
(h) (- 2)-(- 2) = ____________
(i) (- 1) – (+ 1) = ____________
(j) (+ 3) – (- 3) = ____________
उत्तर: (a) (+ 1) – (+ 4) = -3
(b) (0) – (+ 2) = -2
(c) (+ 4) – (+ 1) = +3
(d) (0) – (- 2) = +2
(e) (+ 4) – (- 3) =+7
(f) (- 4) – (- 3) =-1
(g) (- 1) – (+ 2) = -3
(h) (- 2) – (- 2) = 0
(i) (- 1) – (+ 1) = -2
(j) (+ 3) – (- 3) = +6
आइए, पता लगाएँ (Page 251)
1. दिए गए पदों को पूरा कीजिए-
(a) (+ 40) + _____________ = +200
उत्तर: (a) दिया है (+40) + ……………………….. = +200
माना (+ 40) + x = +200
⇒ + x = 200 – 40 = 160
∴ (+ 40) + (+ 160) = +200
(b) (+ 40) + _____________ = -200
उत्तर: (b) दिया है (+40) + …………………….. = -200
माना (+ 40) + x = -200
⇒ x = – 200 – 40 = -240
∴ (+ 40) + (- 240) = -200
(c) (- 50) + _____________ = +200
उत्तर: (c) दिया है (-50) + ……………………. = +200
माना (- 50) + x = +200
⇒ x = + 200 – (- 50) = +250
∴ (- 50) + (+ 250) = +200
(d) (- 50) + _____________ 200
उत्तर: (d) दिया है (-50) + ………………….. = -200
माना (- 50) + x = -200
⇒ x = -200 – (- 50) = -150
∴ (- 50) + (- 150) = -200
(e) (- 200) – (- 40) = _____________
उत्तर: (e) दिया है (− 200) − (− 40) = ………………………
माना (- 200) – (- 40) = x
⇒ (- 200) – (- 40) = -160 = x
∴ (- 200) – (- 40) = -160
(f) (+ 200) – (+ 40) = _____________
उत्तर: (f) दिया है (+ 200 ) – ( + 40) = ………………………
माना (+ 200) – (+ 40) = x
⇒ +160 = x
∴ (+ 200) – (+ 40) = +160
(g) (- 200) – (+ 40) = _____________
उत्तर: (g) दिया है (- 200) – ( + 40) = ………………………
माना (- 200) – (+ 40) = x
⇒ (- 200) + (- 40) = -240 = x
∴ (- 200) + (- 40) = -240
Page 251
इसी प्रकार की लिफ्ट बनाकर या कल्पना करके निम्नलिखित पदों को ज्ञात करने का प्रयास कीजिए-
(a) – 125 + (- 30)
(b) + 105 – (- 55)
(c) + 105 + (+ 55)
(d) + 80 – (- 150)
(e) + 80 + (+ 150)
(f) – 99 – (-200)
(g) – 99 + (+ 200)
(h) + 1500 – (- 1500)
उत्तर: (a) – 125 + (- 30) = – 125 – 30 = -155
(b) + 105 – (- 55) = 105 + 55 = +160
(c) + 105 + (+ 55) = 105 + 55 = +160
(d) + 80 – (- 150) = 80 + 150 = +230
(e) + 80 + (+ 150) 80 + 150 = +230
(f) – 99 – (- 200) = – 99 + 200 = +101
(g) 99 + (+ 200) = – 99 + 200 = +101
(h) + 1500 – (- 1500) + 1500 + 1500 = 3,000
आइए, पता लगाएँ (Page 253, 254)
1. उपरोक्त संख्या रेखा पर 3 धनात्मक तथा 3 ऋणात्मक संख्याओं को चिह्नित कीजिए ।
उत्तर: संख्या रेखा पर:
- धनात्मक संख्याएँ – हम कोई भी तीन धनात्मक संख्याएँ चिह्नित कर सकते हैं, जैसे: 3, 6 और 9।
- ऋणात्मक संख्याएँ – हम कोई भी तीन ऋणात्मक संख्याएँ चिह्नित कर सकते हैं, जैसे: –2, –5 और –8।
2. उपरोक्त 3 ऋणात्मक चिह्नित संख्याओं को दिए गए बॉक्स में लिखिए-
उत्तर: -2, −5 और -8 तीन ऋणात्मक संख्याएँ हैं।
3. क्या 2 > – 3? क्यों? 2 < 3? क्यों?
उत्तर: 2 > – 3, हाँ, 2 > –3 क्योंकि संख्या रेखा पर 2, –3 से दाईं ओर होता है।
धनात्मक संख्या हमेशा ऋणात्मक संख्या से बड़ी होती है।
2 < 3, हाँ, 2 < 3 क्योंकि संख्या 2, 3 से बाईं ओर होती है।
संख्या रेखा पर जो संख्या दाईं ओर होती है, वह बड़ी होती है।
4. हल कीजिए
a. – 5 + 0 b. 7 + (–7) c. –10 + 20
d. 10 –20 e. 7–(–7) f. –8–(–10)?
उत्तर: (a) – 5 + 0
किसी भी संख्या में 0 जोड़ने पर संख्या का मान नहीं बदलता है।
– 5 + 0 = -5
(b) 7 + (- 7)
किसी धनात्मक संख्या को उसके संगत ऋणात्मक संख्या में जोड़ने पर परिणाम 0 आता है।
7 + ( – 7) = 0)
(c) – 10 + 20
विभिन्न चिह्नों वाली संख्याओं को जोड़ने के लिए, बड़े
निरपेक्ष मान से छोटे निरपेक्ष मान को घटाएँ और बड़े निरपेक्ष मान से चिह्न लें।
– 10 + 20 = 10
(d) 10 – 20
किसी बड़ी संख्या को छोटी संख्या से घटाने पर ऋणात्मक परिणाम प्राप्त होता है।
10 – 20 = -10
(e) 7 – ( – 7)
किसी ऋणात्मक संख्या को घटाना उस संख्या के धनात्मक प्रतिरूप को जोड़ने के समान है।
7 – ( – 7) = 7 + 7 = 14
(f) – 8 – (- 10)
किसी ऋणात्मक संख्या को घटाना उस संख्या के संगत धनात्मक संख्या को जोड़ने के समान है।
– 8 – (- 10) = – 8 + 10 = 2
आइए, पता लगाएँ (Page 257)
1. टोकन का उपयोग करते हुए जोड़ को पूरा कीजिए।
(a) (+6) + (+4)
उत्तर: (+6) को दर्शाने के लिए, हम 6 धनात्मक टोकन का उपयोग करते हैं।
(+4) को दर्शाने के लिए, हम 4 धनात्मक टोकन का उपयोग करते हैं।
जब हम इन दोनों को संयोजित (जोड़ते) हैं, तो:
(+6) + (+4) = (+10)
∴ सभी धनात्मक टोकनों को गिनने पर हमें (+10) प्राप्त होता है।
(b) (-3) + (-2)
उत्तर: (–3) को दर्शाने के लिए, हम 3 ऋणात्मक टोकन का उपयोग करते हैं।
(–2) को दर्शाने के लिए, हम 2 ऋणात्मक टोकन का उपयोग करते हैं।
जब हम इन दोनों को संयोजित (जोड़ते) हैं, तो:
(–3) + (–2) = –5
∴ सभी ऋणात्मक टोकनों को गिनने पर हमें (–5) प्राप्त होता है।
(c) (+5) + (-7)
उत्तर: (+5) को दर्शाने के लिए, हम 5 धनात्मक टोकन का उपयोग करते हैं।
(–7) को दर्शाने के लिए, हम 7 ऋणात्मक टोकन का उपयोग करते हैं।
∴ शेष टोकन = (+ 5) + (− 7) = −2
(d) (-2) + (+6)
उत्तर: (-2) को दर्शाने के लिए, हम 2 ऋणात्मक टोकन का उपयोग करते हैं।
(+6) को दर्शाने के लिए, हम 6 धनात्मक टोकन का उपयोग करते हैं
अतः
(- 2) + (+ 6) = +4
शेष टोकन की गिनती करने पर, हमें (+4) टोकन मिलते हैं।
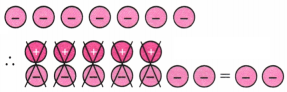
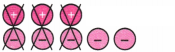
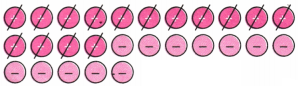
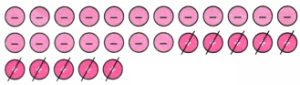
2. नीचे दिए गए टोकन युग्म में से शून्य युग्म को निरस्त (रद्द कीजिए। प्रत्येक स्थिति में लिफ्ट चालक कौन-से तल है? प्रत्येक स्थिति में संगत धनात्मक कथन क्या होगा?
(a) चित्र से हम देखते हैं कि हम तीन शून्य जोड़े हटा सकते हैं।
उत्तर:
चूँकि दो ऋणात्मक टोकन शेष हैं, इसलिए लिफ्ट चालक भूतल से नीचे दूसरे तल पर है।
संगत योग कथन (+ 3) + (− 5) = (−2) है।
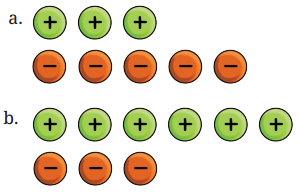
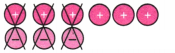
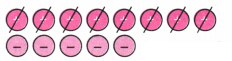
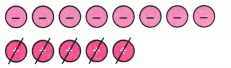
(b) चित्र से हम देखते हैं कि हम तीन शून्य जोड़े हटा सकते हैं।
उत्तर:
चूँकि तीन धनात्मक टोकन शेष हैं, लिफ्ट चालक भूतल से ऊपर तीसरे तल पर है।
संगत योग कथन (+ 6) + (− 3) = (+3) है।
आइए, पता लगाएँ (Page 258)
1. टोकन का उपयोग करके निम्नलिखित अंतरों का मूल्यांकन कीजिए। यह भी जाँचिए कि आपको वही परिणाम मिलता है जो अब आप अन्य तरीकों से जानते हैं। घटाव को पूरा कीजिए-
(a) (+ 10) – ( + 7)
उत्तर: (a) यहाँ, 10 धनात्मक में से 7 धनात्मक घटाएँ।
अत: (+ 10) – (+ 7) = +3
(b) (- 8) – (- 4)
उत्तर: यहाँ, -8 ऋणात्मक से -4 ऋणात्मक घटाएँ।
अतः (-8) – (-4) = -4
(c) (- 9) – (- 4)
उत्तर: (c) यहाँ, -9 ऋणात्मक में से 4 ऋणात्मक घटाएँ।
अतः (- 9) – (4) = -5
(d) (+ 9) – (+ 12)
उत्तर: यहाँ 9 धनात्मक में से 12 धनात्मक घटाव के लिए पर्याप्त टोकन नहीं है।
अत: (+ 9) – (+ 12) = -3
(e) (- 5) – (- 7)
उत्तर: -5 ऋणात्मक से -7 ऋणात्मक घटाव के लिए पर्याप्त टोकन नहीं हैं।
इसलिए, हमने अतिरिक्त दो शून्य जोड़े (1 जोड़ी = एक धनात्मक और एक ऋणात्मक) रखे।
अब हम – 7 ऋणात्मक घटा सकते हैं।
(f) (- 2) – (- 6)
उत्तर: -2 ऋणात्मक से -6 ऋणात्मक घटाव के लिए पर्याप्त टोकन नहीं हैं।
इसलिए, हमने अतिरिक्त चार शून्य जोड़े (1 जोड़ी = एक धनात्मक और एक ऋणात्मक) डाले।
अब हम – 6 ऋणात्मक घटा सकते हैं।
अत: (- 2) – (- 6) = +4
2. घटाव को पूरा कीजिए-
(a) (- 5) – (- 7)
उत्तर: (a) -5 ऋणात्मक से -7 ऋणात्मक घटाव के लिए पर्याप्त टोकन नहीं हैं।
इसलिए, हमने अतिरिक्त दो शून्य जोड़े (1 जोड़ी = एक धनात्मक और एक ऋणात्मक) रखे।
अब हम – 7 ऋणात्मक घटा सकते हैं।
अत: (-5) – (-7) = +2
(b) (+10) – (+13)
उत्तर: 10 धनात्मक में से 13 धनात्मक घटाव के लिए पर्याप्त टोकन नहीं हैं।
इसलिए, हमने अतिरिक्त 3 शून्य जोड़े (1 जोड़ी = एक धनात्मक और एक ऋणात्मक) डाले।
अब हम 13 धनात्मक घटा सकते हैं।
अत: (+ 10) – (+ 13) = -3
(c) (-7) – (-9)
उत्तर: -7 ऋणात्मक से -9 ऋणात्मक घटाव के लिए पर्याप्त टोकन नहीं है।
इसलिए, हमने अतिरिक्त दो शून्य जोड़े (1 जोड़ी = एक धनात्मक और एक ऋणात्मक) रखे।
अब हम -9 ऋणात्मक घटा सकते हैं।
अत: (- 7) – (- 9) = +2
(d) (+3) – (+8)
उत्तर: 3 धनात्मक में से 8 धनात्मक घटाव के लिए पर्याप्त टोकन नहीं है।
इसलिए, हमने अतिरिक्त 5 शून्य जोड़े (1 जोड़ी = एक धनात्मक और एक ऋणात्मक) डाले।
अब हम 8 धनात्मक घटा सकते हैं।
अत: (+ 3) – (+ 8) = -5
(e) (-2) – (-7)
उत्तर: -2 ऋणात्मक से -7 ऋणात्मक घटाव के लिए पर्याप्त टोकन नहीं हैं।
इसलिए, हमने अतिक्ति दो शून्य जोड़े (1 जोड़ी एक धनात्मक और एक ऋणात्मक) रखे।
अब हम -7 ऋणात्मक घटा सकते हैं।
अतः (- 2) – (-7) = +5
(f) (+3) – (+15)
उत्तर: 3 धनात्मक में से 15 धनात्मक घटाव के लिए
पर्याप्त टोकन नहीं हैं।
इसलिए, हमने अतिरिक्त 12 शून्य जोड़े (1 जोड़ा = एक धनात्मक और एक ऋणात्मक) डाले।
अब हम 15 धनात्मक घटा सकते हैं।
अतः (+ 3 ) – (+ 15) = -12
आइए, पता लगाएँ (Page 259)
1. घटाने का प्रयास कीजिए- – 3 – (+ 5)
आपको कितने शून्य के जोड़ें रखने होंगे? इसका परिणाम क्या होगा ?
उत्तर: हमें -3 ऋणात्मक से 5 धनात्मक निकालने हैं। लेकिन पर्याप्त धनात्मक नहीं हैं।
इसलिए, हमने अतिरिक्त 5 शून्य जोड़े (1 जोड़ी = एक धनात्मक और एक ऋणात्मक) डाले।
अब हम 5 धनात्मक निकाल सकते हैं।
अतः – 3 (+ 5) = -8
2. टोकन का उपयोग करते हुए निम्न का मूल्यांकन कीजिए।
(a) (- 3) – (+ 10)
(a) (-3) – (+10)
उत्तर: हमें -3 ऋणात्मक से 10 धनात्मक निकालने हैं। लेकिन पर्याप्त धनात्मक नहीं हैं।
इसलिए, हमने अतिरिक्त 10 शून्य जोड़े ( 1 जोड़ी एक धनात्मक और एक ऋणात्मक) रखे।
अब हम 10 धनात्मक निकाल सकते हैं।
अतः (- 3) – (+ 10) = -13
(b) (+ 8) – (- 7)
उत्तर: हमें 8 धनात्मक में से -7 ऋणात्मक निकालने है। लेकिन पर्याप्त ऋणात्मक नहीं है।
इसलिए, हमने अतिरिक्त 7 शून्य जोड़े (1 जोड़ी = एक धनात्मक और एक ऋणात्मक) रखे।
अब हम -7 ऋणात्मक निकाल सकते हैं।
अतः (+ 8) – (- 7) = 15
(c) (- 5) – (+ 9)
उत्तर: हमें -5 ऋणात्मक में से 9 धनात्मक निकालने हैं। लेकिन पर्याप्त धनात्मक नहीं हैं।
इसलिए, हमने अतिरिक्त 9 शून्य जोड़े (1 जोड़ा = एक धनात्मक और एक ऋणात्मक) रखे।
अब हम 9 धनात्मक निकाल सकते हैं।
अतः 5 – (+9 ) = -14
(d) (- 9) – (+ 10)
उत्तर: हमें – 9 ऋणात्मक में से 10 धनात्मक निकालने हैं। लेकिन पर्याप्त धनात्मक नहीं हैं।
इसलिए, हमने अतिरिक्त 10 शून्य जोड़े (1 जोड़ा एक धनात्मक और एक ऋणात्मक) रखे।
अब हम 10 धनात्मक निकाल सकते हैं।
अतः – 9 – (+ 10) = −19
(e) (+ 6) – (- 4)
उत्तर: हमें 6 धनात्मक में से -4 ऋणात्मक निकालने हैं। लेकिन पर्याप्त ऋणात्मक नहीं हैं।
इसलिए, हमने अतिरिक्त 4 शून्य जोड़े (1 जोड़ी एक धनात्मक और एक ऋणात्मक) रखे।
अब हम – 4 धनात्मक निकाल सकते हैं।
अत: (+ 6) – (- 4) = 10
(f) (- 2 ) – (+ 7)
उत्तर: हमें -2 ऋणात्मक में से 7 धनात्मक निकालने हैं।
लेकिन पर्याप्त धनात्मक नहीं हैं।
इसलिए, हमने अतिरिक्त 7 शून्य जोड़े (1 जोड़ा = एक धनात्मक और एक ऋणात्मक) रखे।
अब हम 7 धनात्मक निकाल सकते हैं।
अत: (-2) – (+7) = -9
आइए, पता लगाएँ (Page 260)
1. माना आप ₹ 0 के साथ अपना बैंक खाता खोलते हैं, इसके पश्चात् आप उसमें ₹ 30, ₹ 40 और ₹ 50 जमा करवाते हैं और ₹ 40, ₹ 50 और ₹ 60 की निकासी करते हैं। अब आपके बैंक खाते में कितनी जमा राशि शेष है?
उत्तर: जमा (क्रेडिट):
कुल जमा = ₹30 + ₹40 + ₹50 = ₹120
निकासी (डेबिट):
कुल निकासी = ₹40 + ₹50 + ₹60 = ₹150
अब कुल शेष राशि:
₹120 – ₹150 = –₹30
आपके बैंक खाते में ₹ –30 शेष है, यानि आप ₹30 ऋण (उधार) में हैं।
2. माना आप ₹ 0 के साथ अपना बैंक खाता खोलते हैं और अपने उसी खाते में से ₹ 1, 2, 4, 8, 16, 32, 64 और 128 निकाल लेते हैं, इसके पश्चात् आप एक बार में ₹ 256 रूपए जमा कर देते हैं। अब आपके बैंक खाते में कितनी जमा राशि शेष है?
उत्तर: निकासी (डेबिट):
₹1, ₹2, ₹4, ₹8, ₹16, ₹32, ₹64, ₹128
कुल निकासी =
1 + 2 + 4 + 8 + 16 + 32 + 64 + 128 = ₹255
जमा (क्रेडिट): ₹256
∴ शेष = जमा – निकासी
= ₹ 256 – 255 = ₹ 1
इसलिए, आपके बैंक खाते का शेष ₹ 1 है।
3. आपके बैंक खाते में प्रायः धनात्मक जमा राशि अधिक अच्छी क्यों मानी जाती है? ऐसी कौन-सी परिस्थितियाँ हो सकती हैं, जिनके तहत अस्थायी रूप से ऋणात्मक (निकासी) शेष जमा राशि सार्थक हो सकती है?
उत्तर: अपने बैंक खाते में धनात्मक जमा राशि रखना आमतौर पर अच्छा होता है क्योंकि-
ओवरड्राफ्ट शुल्क से बचाना – यदि आपके खाते की राशि ऋणात्मक हो जाती है तो कई बैंक शुल्क लगाते हैं।
वित्तीय सुरक्षा प्रदान करना – धनात्मक जमा राशि यह सुनिश्चित करती है कि आपके पांस अप्रत्याशित व्यय या आपात स्थितियों के लिए धन उपलब्ध है।
अच्छा वित्तीय रिकॉर्ड रखना- धनात्मक जमा राशि बनाए रखने से आपके वित्तीय स्कोर को बेहतर बनाने में मदद मिल सकती है, जिससे भविष्य में ऋण या क्रेडिट- कार्ड प्राप्त करना आसान हो जाता है।
कुछ विशिष्ट परिस्थितियाँ हो सकती हैं जहाँ अस्थायी रूप से ऋणात्मक शेष राशि रखने पर विचार किया जा सकता है।
- ओवरड्राफ्ट सुरक्षा – कुछ बैंक ओवरड्राफ्ट सुरक्षा प्रदान करते हैं जो चेक बाउंस या घोषित लेनदेन से बचने में. मदद कर सकती है।
- नियोजित बड़े व्यय – यदि आप जानते हैं कि आपके पास शीघ्र ही बड़ी आय होगी और आपको आवश्यक खरीददारी करनी होगी तो अस्थायी ऋणात्मक जमा राशि स्वीकार्य हो सकता है।
आइए, पता लगाएँ (Page 260, 261)
1. भौगोलिक प्रतिच्छेद को देखते हुए उनकी संबंधित ऊँचाइयाँ लिखिए-
उत्तर: आपको ग्राफ में दिए गए बिंदुओं A से G तक की ऊँचाई का अनुमान लगाना है।
इसके लिए ऊर्ध्वाधर रेखा (Vertical Axis) की सहायता लें और प्रत्येक बिंदु की स्थिति के अनुसार उसकी ऊँचाई तय करें।
बिंदुओं की अनुमानित ऊँचाई इस प्रकार है:
- A → +1500 मीटर
- B → –500 मीटर
- C → +300 मीटर
- D → –1200 मीटर
- E → +1200 मीटर
- F → –200 मीटर
- G → +100 मीटर
2. इस भौगोलिक प्रतिच्छेद में सबसे उच्चतम बिंदु एवं सबसे निम्नतम बिंदु कौन-सा है?
उत्तर: भौगोलिक प्रतिच्छेद में उस बिंदु को पहचानिए जो समुद्र तल से ऊपर स्थित है।
बिंदु A सबसे अधिक ऊँचाई पर है, इसलिए यह सबसे ऊँचा बिंदु दर्शाता है।
इसी तरह, समुद्र तल से नीचे स्थित बिंदुओं में
बिंदु D सबसे गहराई में है, इसलिए यह सबसे निचला बिंदु दर्शाता है।
3. क्या आप बिंदुओं A, B, …, G को ऊँचाइयों के अवरोही (घटते क्रम में लिख सकते हैं? क्या आप बिंदुओं को ऊँचाइयों के आरोही (बढ़ते क्रम में लिख सकते हैं?
उत्तर: हाँ, आइए बिंदुओं A से G तक की ऊँचाइयों को क्रम में लिखते हैं:
अवरोही क्रम (घटते हुए क्रम में): (सबसे ऊँचा से सबसे नीचा)
A (+1500 m) > E (+1200 m) > C (+300 m) > G (+100 m) > F (–200 m) > B (–500 m) > D (–1200 m)
क्रम: A, E, C, G, F, B, D
आरोही क्रम (बढ़ते हुए क्रम में): (सबसे नीचा से सबसे ऊँचा)
D (–1200 m) < B (–500 m) < F (–200 m) < G (+100 m) < C (+300 m) < E (+1200 m) < A (+1500 m)
क्रम: D, B, F, G, C, E, A
4. पृथ्वी पर समुद्र तल से सबसे ऊँचा स्थान कौन-सा है? इसकी ऊँचाई कितनी है ?
उत्तर: पृथ्वी पर समुद्र तल से सबसे ऊँचा स्थान है:
माउंट एवरेस्ट (Mount Everest)
स्थान: हिमालय पर्वत शृंखला (नेपाल और तिब्बत/चीन की सीमा पर)
ऊँचाई: 8848.86 मीटर (समुद्र तल से ऊपर)
5. भूमि या महासागर तल पर समुद्र तल के सापेक्ष सबसे निम्नतम बिंदु क्या है? इसकी ऊँचाई कितनी है? (यह ऊँचाई ऋणात्मक होनी चाहिए।)
उत्तर: सबसे निम्नतम बिंदु:
मैरिआना ट्रेंच (Mariana Trench) में स्थित चैलेंजर डीप (Challenger Deep)
स्थान: पश्चिमी प्रशांत महासागर
ऊँचाई (गहराई): –11,000 मीटर (लगभग)
(समुद्र तल से नीचे)
यह पृथ्वी पर ज्ञात सबसे गहरी जगह है और यह ऊँचाई ऋणात्मक (-) मानी जाती है क्योंकि यह समुद्र तल से नीचे है।
आइए, पता लगाएँ (Page 262)
1. क्या आप जानते हैं कि भारत में कुछ ऐसे स्थान भी हैं जहाँ कभी-कभी तापमान 0 °C से नीचे चला जाता है ? भारत में ऐसे स्थानों का पता लगाइए जहाँ तापमान सामान्यतः बार 0 °C से भी नीचे पहुँच जाता है। इन स्थानों में क्या समानता है? अन्य स्थानों की तुलना में यहाँ अधिक ठंड क्यों होती है?
उत्तर: ठंडी जलवायु वाले प्रमुख क्षेत्र:
लद्दाख:
यह क्षेत्र अपनी कठोर सर्दियों के लिए प्रसिद्ध है। यहाँ का तापमान अक्सर 0°C से काफी नीचे चला जाता है।
हिमाचल प्रदेश:
राज्य के ऊँचाई वाले विशेषकर उत्तरी भागों में तापमान सर्दियों में शून्य से नीचे चला जाता है।
जम्मू और कश्मीर:
यहाँ के पहाड़ी क्षेत्रों में अत्यधिक ठंड पड़ती है, विशेषकर लद्दाख और गुलमर्ग जैसे इलाकों में।
सिक्किम:
पहाड़ी राज्य होने के कारण सिक्किम के कई स्थानों पर तापमान शून्य से नीचे दर्ज किया जाता है।
अरुणाचल प्रदेश:
इसके ऊँचे पर्वतीय क्षेत्रों में भी ठंडी जलवायु देखने को मिलती है, जहाँ तापमान अक्सर 0°C से नीचे होता है।
इन सभी क्षेत्रों की एक जैसी विशेषताएँ:
ये सभी हिमालयी क्षेत्र में स्थित हैं।
इनकी ऊँचाई अधिक है, जिससे तापमान स्वाभाविक रूप से कम रहता है।
तापमान कम होने के कारण:
ऊँचाई:
जैसे-जैसे हम ऊँचाई पर जाते हैं, वातावरण पतला होता जाता है और गर्मी कम हो जाती है, जिससे तापमान घटता है।
भूमध्य रेखा से दूरी:
ये क्षेत्र भूमध्य रेखा से दूर हैं, इसलिए वहाँ सूर्य की किरणें सीधे नहीं पड़तीं, जिससे तापमान अपेक्षाकृत कम रहता है।
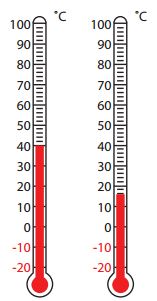
2. लद्दाख के लेह क्षेत्र में सर्दी के समय अत्यधिक ठंड हो जाती है। नीचे दी गई सारणी को देखिए, यह लेह के नवंबर माह के एक दिन के विभिन्न समयों के तापमान को दर्शाती है। साथ दिन और रात के सही समय के साथ संबंधित तापमान का मिलान कीजिए।
उत्तर:
आइए, पता लगाएँ (Page 263, 264)
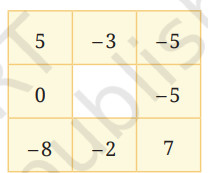
1. उपरोक्त दूसरे ग्रिड के लिए गणना कीजिए और सीमा योग ज्ञात कीजिए।
उत्तर: दिया गया ग्रिड:
यह एक 3 x 3 संख्याओं का वर्ग है, जिसमें:
3 पंक्तियाँ (rows)
3 स्तंभ (columns)
हर पंक्ति और हर स्तंभ का योग समान होना चाहिए।
सीमा योग (Magic Sum) कैसे निकालें:
ऊपरी पंक्ति:
5 + (–3) + (–5) = –3
निचली पंक्ति:
(–8) + (–2) + 7 = –3
बायाँ स्तंभ:
5 + 0 + (–8) = –3
दायाँ स्तंभ:
(–5) + (–5) + 7 = –3
हर पंक्ति और स्तंभ का योग है –3
इसलिए इस ग्रिड का सीमा योग (Magic Sum) है: –3
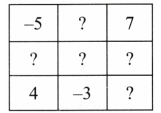
2. आवश्यक सीमा योग बनाने के लिए ग्रिड को पूर्ण कीजिए-
उत्तर:
सीमा योग +4 है
स्पष्टीकरण:
हमने लुप्त संख्याएँ इस प्रकार भरीं कि हर पंक्ति और स्तंभ का योग +4 रहे।
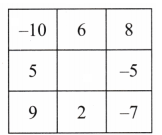
उदाहरण के लिए, पहले ग्रिड में ऊपरी पंक्ति में –10 पहले से मौजूद था।
अब हमें शेष दो संख्याएँ ऐसी भरनी थीं कि कुल योग +4 हो।
इसलिए:
–10 + 6 + 8 = +4,
इसलिए लुप्त संख्याएँ 6 और 8 होनी चाहिए।
इसी तरह बाकी दो ग्रिड आप खुद भरने की कोशिश करें और हर पंक्ति तथा स्तंभ का योग दिए गए सीमा योग के बराबर बनाएँ।
3. उपरोक्त अंतिम ग्रिड में -4 सीमा योग प्राप्त करने के लिए एक से अधिक तरीके बताइए ।
उत्तर: अंतिम ग्रिड को सीमा योग -4 से भरने के कई तरीके हैं, यहाँ दो उदाहरण दिए गए हैं-
4. कौन – सी अन्य ग्रिड विभिन्न विधियों से भरी जा सकती है? इसके क्या कारण हो सकते हैं?
उत्तर: वे ग्रिड जिनमें अधिक संख्या में बॉक्सों को बिना भरे छोड़ दिया गया है, क्योंकि ऐसी स्थिति में बॉक्सों को संख्याओं से भरने के विकल्प अधिक होते हैं।
उदाहरणार्थ, दूसरी ग्रिड को यहाँ किसी अन्य विधि से नहीं भरा जा सकता है।
5. एक सीमा पूर्णांक वर्ग पहेली बनाइए और इसे पूर्ण करने के लिए सहपाठियों को चुनौती दीजिए।
उत्तर: पहेली
सीमा योग: 2
(अतिरिक्त नोट: अंतिम ग्रिड को भरने के दो अधिक तरीके हो सकते हैं।
अलग-अलग क्रम योग के साथ बड़े ग्रिड बनाने के अधिक जटिल और चुनौतीपूर्ण पहेलियाँ बन सकती हैं।)
आइए, पता लगाएँ (Page 264)
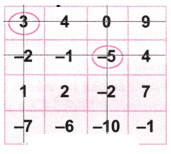
1. पुनः प्रयास कीजिए, इस बार अलग संख्याएँ चुनिए । आपको इन संख्याओं का क्या योग प्राप्त हुआ? क्या यह पहले से भिन्न है ? कुछ और बार प्रयास कीजिए।
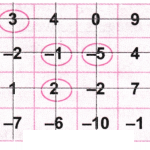
उत्तर: आइए संख्या – 5 पर गोला बनाइए।
अब खेल के अनुसार, आइए संख्या – 5 वाले पंक्ति और स्तंभ को काट दीजिए।
आइए फिर से संख्या 3 पर गोला लगाइए।
आइए संख्या 3 के साथ पंक्ति और स्तंभ को काट दीजिए।
आइए फिर से संख्या – 1 पर गोला बनाइए।
आइए संख्या 1 के साथ पंक्ति और स्तंभ को काट दीजिए
आइए फिर से शेष संख्या 2 पर गोला लगाइए।
आइए संख्या 2 के साथ पंक्ति और स्तंभ को काट दीजिए।
अब आइए गोले में बनी संख्याओं को जोड़ें =
– (5) + 3 + (- 1) + (2) = – 6 + 5 = -1
इसलिए हमें समान मान (1) मिलता है।
अब स्वयं प्रयास करें।
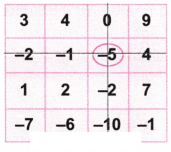
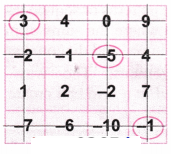
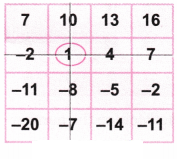
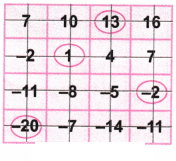
2. नीचे दी गई ग्रिड के साथ भी इसी तरह का खेल खेलिए। आप क्या उत्तर प्राप्त करते हैं?
उत्तर: (a) आइए संख्या 1 पर गोला लगाइए।
अब खेल के अनुसार, आइए संख्या 1 वाली पंक्ति और स्तंभ को काट दीजिए।
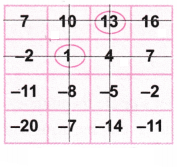
आइए फिर से संख्या 13 पर गोला बनाइए।
आइए संख्या 13 वाली पंक्ति और स्तंभ को काट दीजिए।
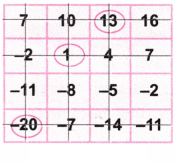
आइए फिर से संख्या -20 पर गोला लगाइए। आइए संख्या -20 वाली पंक्ति और स्तंभ को काट दीजिए।
आइए फिर से शेष संख्या -2 पर गोला लगाइए।
आइए संख्या -2 वाली पंक्ति और स्तंभ को काट दीजिए।
अब गोलाकार संख्याओं को जोड़ें = 1 + 13 – 20 – 2 = 14 – 22 = -8 जो कि अभीष्ट उत्तर है।
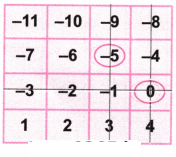
उत्तर: (b) आइए संख्या 0 पर गोला लगाइए।
अब खेल के अनुसार, आइए संख्या0 वाली पंक्ति और स्तंभ को काट दीजिए
फिर से आइए संख्या -5 पर गोला बनाइए।
आइए संख्या -5 वाली पंक्ति और स्तंभ को काट दीजिए।
फिर से आइए संख्या 1 पर गोला बनाइए।
आइए संख्या 1 वाली पंक्ति और स्तंभ को काट दीजिए।
फिर से आइए शेष संख्या – 10 पर गोला बनाइए।
आइए संख्या – 10 वाली पंक्ति और स्तंभ को काट दीजिए।
अब आइए घेरे गए अंकों को जोड़ें
= 0 + (- 5) + 1 (- 10) = -14
जो कि अभीष्ट उत्तर है ।
3. इन ग्रिडों में क्या विशेष हो सकता है? क्या संख्याओं में जादू है या इन्हें व्यवस्थित करने के तरीके में जादू है या दोनों में हैं? क्या आप ऐसे और ग्रिड बना सकते हैं?
उत्तर: संख्याएँ:
ग्रिड में संख्याएँ अक्सर किसी खास पैटर्न या क्रम में होती हैं।
उदाहरण के लिए, जादुई वर्ग में हर पंक्ति, स्तंभ और तिरछी रेखा का योग बराबर होता है।
व्यवस्था:
संख्याएँ जिस तरतीब से रखी जाती हैं, उससे ग्रिड में एक संतुलन और सुंदरता दिखाई देती है,
जो देखने में अच्छा लगता है।
इसलिए, संख्या और उनकी सही जगह ग्रिड को खास बनाती हैं।
आइए, पता लगाएँ (Page 265)
1. दिए गए युग्मों के बीच सभी पूर्णांकों को बढ़ते क्रम में लिखिए।
(a) 0 और -7
(b) -4 और 4
(c) -8 और -15
(d) -30 और -23
उत्तर: (a) 0 और –7 के बीच:
–6, –5, –4, –3, –2, –1
(b) –4 और 4 के बीच:
–3, –2, –1, 0, 1, 2, 3
(c) –8 और –15 के बीच:
–14, –13, –12, –11, –10, –9
(d) –30 और –23 के बीच:
–29, –28, –27, –26, –25, –24
2. ऐसी तीन संख्याएँ बताइए जिनका योग -8 है।
उत्तर: तीन संख्याएँ जिनका योग -8 है वे हैं -10, 1 और 3 जब हम उन्हें एक साथ जोड़ते हैं, तो हमें – 10 + 1 + 1 = -8 मिलता है।
3. यहाँ दो पासे हैं जिनके फलकों पर संख्याएँ दर्शाई गई हैं- -1, 2, 3, 4, -5, 6 इन पासों को उछालने पर सबसे छोटा संभावित योग – 10 = (- 5) + (- 5) है और सबसे बड़ा संभावित योग 12 = (6) + (6) है। इन दो पासों पर संख्याओं को जोड़ने से (-10) और (+12) के बीच की कुछ संख्याएँ प्राप्त करना संभव नहीं है। ऐसी संख्याओं का पता लगाइए।
उत्तर: आइए उन योगों को खोजें जो इन दो पासों को घुमाने पर संभव नहीं हैं।
पासों के चेहरे हैं: -1, 2, -3, 4, -5 और 6
सबसे पहले, आइए सभी संभावित योगों को सूचीबद्ध करें-
दो ऋणात्मक संख्याओं का योग:
यहाँ ऋणात्मक संख्याएँ हैं: –1, –3, –5,…..
अब इनका आपस में योग करते हैं:
- –1 + (–1) = –2
- –1 + (–3) = –4
- –1 + (–5) = –6
- –3 + (–3) = –6
- –3 + (–5) = –8
- –5 + (–5) = –10
एक ऋणात्मक संख्या तथा एक घनात्मक संख्या का योग-
- (- 1) + 2 = 1
- (- 1) + 4 = 3
- (- 1) + 6 = 5
- (- 3) + 2 = -1
- (- 3) + 4 = 1
- (- 3) + 6 = 3
- (- 5) + 2 = -3
- (- 5) + 4 =-1
- (-5) + 6 = 1
दो धनात्मक संख्याओं का योग-
- 2 + 2 = 4
- 2 + 4 = 6
- 2 + 6 = 8
- 4 + 4 = 8
- 4 + 6 = 10
- 6 + 6 = 12
अब, आरोही क्रम में सभी संभावित योगों को सूचीबद्ध करें-
- -10, -8, -6, -4, -3, -2, -1, 1, 3, 4, 5, 6, 10, 12
– 10 और 12 के बीच संख्याओं का योग जो प्राप्त करना संभव नहीं है-
- -9, -7, -5, 0, 2, 7, 9, 11
4. इन्हें हल कीजिए-
उत्तर: (a) 8 – 13 = -5
(b) -8 – (13) = -8 – 13 = -21
(c) -13 – (-8) = -13 + 8 = -5
(d) (-13) + (-8) = -13 – 8 = -21
(e) 8 + (-13) = 8 – 13 = -5
(f) -8 – (-13) = -8 + 13 = 5
(g) (13) – 8 = 13 – 8 = 5
(h) 13 – (-8) = 13 + 8 = 21
5. निम्नलिखित के वर्ष ज्ञात कीजिए?
(a) वर्तमान वर्ष से 150 वर्ष पूर्व कौन – सा वर्ष था? …………………….
(b) वर्तमान वर्ष से 2200 वर्ष पूर्व कौन – सा वर्ष था? ………………..
संकेत याद रखिए कि कोई 0 वर्ष नहीं था।
(c) 680 ईसा पूर्व से 320 वर्ष बाद कौन-सा वर्ष होगा? ……………………….
उत्तर: (a) वर्तमान वर्ष (2024) से 150 वर्ष पूर्व
(2024 – 150 = 1874)
तो, 150 वर्ष पहले, वर्ष 1874 था।
(b) वर्तमान वर्ष (2024) से 2200 वर्ष पूर्व- चूँकि कोई वर्ष 0 नहीं था, इसलिए हमें अपनी गणना में इसका हिसाब रखना होगा-
(2024 – 2200 = -176)
177 ईसा पूर्व (आम युग से पहले) वर्ष – 176 से मेल खाता है।
इसलिए, 2200 साल पहले, यह वर्ष 177 ईसा पूर्व था।
(c) चूँकि ईसा पूर्व ईसा से पहले का वर्ष है, इसलिए 680 ईसा पूर्व = -680
अतः 680 ईसा पूर्व के 320 वर्ष बाद = – 680 + 320 = -360 = 360 ईसा पूर्व।
6. निम्नलिखित अनुक्रम को पूरा कीजिए –
a. (–40), (–34), (–28), (–22), ____, ____, ____
b. 3, 4, 2, 5, 1, 6, 0, 7, ____, ____, ____
c. ____, ____, 12, 6, 1, (–3), (–6), ____, ____, ____, ____
a. (–40), (–34), (–28), (–22), ____, ____, ____
उत्तर: यहाँ हर संख्या में +6 जोड़ा जा रहा है:
- –40 → –34 (+6)
- –34 → –28 (+6)
- –28 → –22 (+6)
अब आगे:
- –22 + 6 = –16
- –16 + 6 = –10
- –10 + 6 = –4
–16, –10, –4
b. 3, 4, 2, 5, 1, 6, 0, 7, ____, ____, ____
उत्तर: यहाँ दो पैटर्न साथ चल रहे हैं:
- एक पैटर्न घटता है: 3, 2, 1, 0, –1, –2, –3…
- दूसरा पैटर्न बढ़ता है: 4, 5, 6, 7, 8, 9, 10…
तो अगली संख्याएँ होंगी:
- –1, 8
- –2, 9
- –3, 10
हम केवल तीन भरनी हैं, तो: –1, 8, –2
c. ____, ____, 12, 6, 1, (–3), (–6), ____, ____, ____, ____
उत्तर: अब देखें:
- 12 → 6 (–6)
- 6 → 1 (–5)
- 1 → –3 (–4)
- –3 → –6 (–3)
घटते हुए क्रम में घटाव भी 1-1 से घट रहा है: –6, –5, –4, –3,…
आगे:
- –6 → –8 (–2)
- –8 → –9 (–1)
- –9 → –9 (0)
- –9 → –8 (+1)
अब पीछे चलें:
- 12 → ___ ( +6 ) = 18
- 18 → ___ ( +7 ) = 25
25, 18, 12, 6, 1, –3, –6, –8, –9, –9, –8
7. यहाँ छह पूर्णांक कार्ड हैं (+1), (+7), (+18), (-5), (-2), (-9) आप इनमें से किसी भी कार्ड का चयन कर सकते हैं तथा जोड़ और घटा के उपयोग द्वारा एक पद बनाइए।
यहाँ एक पद है- (+ 18) + (+1) – (+7) – (- 2) जिसका मान (+14) है। दिए गए काईस से एक से अधिक कार्ड का चयन कीजिए और एक पद बनाइए जिसका मान (-30) के आस-पास हो।
उत्तर: आइए दिए गए कार्ड का उपयोग करके एक ऐसा व्यंजक बनाने का प्रयास करें जो (-30) के जितना संभव हो सके उतना करीब हो (+1, +7, +18, -5 -2, -9)
एक संभावित व्यंजक है (- 9) + (- 5) + (- 2) + (- 18) + (+ 1)
आइए चरण दर चरण मान की गणना करें-
1. (- 9) + (- 5) = -14
2. 14 + (- 2) = -16
3. 16 + (- 18) = -34
4. 34 + (+ 1) = -33
अतः इस व्यंजक का मान (-33) है, जो (-30) के काफी करीब है।
8. दो धनात्मक पूर्णांकों का योग सदैव धनात्मक होता है लेकिन एक (धनात्मक पूर्णांक) – (धनात्मक पूर्णांक)
धनात्मक या ऋणात्मक हो सकता है। आप निम्न के विषय में क्या कह सकते हैं-
a. (धनात्मक)–(ॠणात्मक)
b. (धनात्मक) + (ॠणात्मक)
c. (ॠणात्मक) + (ॠणात्मक)
d. (ॠणात्मक)–(ॠणात्मक)
e. (ॠणात्मक)–(धनात्मक)
f. (ॠणात्मक) + (धनात्मक)
उत्तर: (a) (धनात्मक) – (ऋणात्मक)
उदाहरण: 5 – (–3) = 5 + 3 = 8
उत्तर: हमेशा धनात्मक
नियम: ऋणात्मक संख्या घटाने का मतलब है उसे जोड़ना।
(b) (धनात्मक) + (ऋणात्मक)
उदाहरण: 7 + (–4) = 3
उत्तर धनात्मक या ऋणात्मक हो सकता है — यह इस पर निर्भर करता है कि कौन-सी संख्या बड़ी है।
यदि धनात्मक बड़ा है → उत्तर धनात्मक,
यदि ऋणात्मक बड़ा है → उत्तर ऋणात्मक
(c) (ऋणात्मक) + (ऋणात्मक)
उदाहरण: –3 + (–5) = –8
उत्तर: हमेशा ऋणात्मक
नियम: दो ऋणात्मक संख्याओं को जोड़ने पर बड़ा ऋणात्मक उत्तर मिलता है।
(d) (ऋणात्मक) – (ऋणात्मक)
उदाहरण: –4 – (–2) = –4 + 2 = –2
उत्तर ऋणात्मक, धनात्मक या 0 हो सकता है — यह इस पर निर्भर करता है कि कौन-सी संख्या बड़ी है।
(e) (ऋणात्मक) – (धनात्मक)
उदाहरण: –3 – 5 = –8
उत्तर: हमेशा ऋणात्मक
नियम: ऋणात्मक से और धनात्मक घटाने का अर्थ है और अधिक ऋणात्मक बनना।
(f) (ऋणात्मक) + (धनात्मक)
उदाहरण: –6 + 4 = –2
उत्तर धनात्मक या ऋणात्मक हो सकता है — यह इस पर निर्भर करता है कि कौन-सी संख्या बड़ी है।
9. इस लड़ी में 100 टोकन हैं, जो एक विशेष पैटर्न में व्यवस्थित किए गए हैं. इस लड़ी का मान क्या है?
आइये, लड़ी के अनुक्रम का विश्लेषन करें -3, -2, 3, -2, 3, -2
उत्तर: आइए 5 टोकन का एक पैटर्न लें क्योंकि यह दोहराया जा रहा है, कुल 3 – 2 = 1 है
लड़ी में 100 टोकन हैं।
कुल पैटर्न = \( \frac{100}{5} \) = 20 पैटर्न
अतः 1 पैटर्न का योग = 1
अतः, लड़ी का मान = 1 × 20 = 20
आइए, पता लगाएँ (Page 268)
1. क्या आप ब्रह्मगुप्त के नियमों को बेला की मजेदार इमारत या संख्या रेखा के अनुसार स्पष्ट कर सकते हो?
उत्तर: आइए बेला की मजेदार इमारत और संख्या रेखा की अवधारणा का उपयोग करके, ब्रह्मगुप्त के नियमों को समझे। ब्रह्मगुप्त के नियम मुख्य रूप से धनात्मक और ऋणात्मक संख्याओं से जुड़े संचालन से संबंधित हैं। यहाँ हम उन्हें कैसे समझ सकते हैं-
ब्रह्मगुप्त के नियम-
i. धनात्मक संख्याओं का योग
- नियम – दो धनात्मक संख्याओं को जोड़ने पर एक धनात्मक संख्या प्राप्त होती है।
- बेला की इमारत – यदि बेला तीसरे तल से शुरू करती है और दो तल ऊपर जाती है, तो वह पांचवे तल पर पहुँच जाती है।
- संख्या रेखा – संख्या रेखा पर 2 जोड़कर 3 से 5 तक जाना।
उदाहरण- 3 + 2 = 5
ii. ऋणात्मक संख्याओं का योग
- नियम – दो ऋणात्मक संख्याओं को जोड़ने पर एक ऋणात्मक संख्या प्राप्त होती है।
- बेला की इमारत – यदि बेला भूतल से 3 तल नीचे (-3) से शुरू करती है और 2 तल और नीचे जाती है, तो वह भूतल से 5 तल नीचे (−5) पहुँच जाती है।
- संख्या रेखा – 2 जोड़कर – 3 से – 5 तक जाना।
उदाहरण – – 3 + (−2) = -5
iii. एक धनात्मक और एक ऋणात्मक संख्या का योग
- नियम – बड़े निरपेक्ष मान से छोटे निरपेक्ष मान को घटाएँ और बड़े निरपेक्ष मान का चिह्न रखें।
- बेला की इमारत – यदि बेला तीसरे तल से शुरू करती है और 5 तल नीचे जाती है, तो वह भूतल से 2 तल नीचे (−2) पहुँच जाती है।
- संख्या रेखा – 5 जोड़कर 3 से -2 तक जाना।
उदाहरण – 3 + (-5) = −2
iv. एक ऋणात्मक संख्या से एक धनात्मक संख्या का घटाव-
- नियम – एक ऋणात्मक संख्या से एक धनात्मक घटाना दो संख्याओं को जोड़ने और ऋणात्मक चिह्न को रखने के समान है।
- बेला की इमारत-यदि बेला भूतल से 3 तल नीचे है (-3) और 2 तल और नीचे चली जाती है, तो वह भूतल से 5 तल नीचे पहुँच जाती है (-5)।
- संख्या रेखा – 2 घटाकर 3 से 5 तक जाना।
उदाहरण- – 3 – 2 = −5
v. एक धनात्मक संख्या से एक ऋणात्मक संख्या का घटाव
- नियम- एक धनात्मक संख्या से एक ऋणात्मक संख्या घटाना दो संख्याओं को जोड़ने जैसा है।
- बेला की इमारत यदि बेला तीसरे तल से शुरू करती है और दो तल ऊपर जाती है, तो वह पांचवे तल पर पहुँच जाती है।
- संख्या रेखा – -2 घटाकर 3 से 5 तक जाना।
उदाहरण – 3 – (-2) = 5
vi. एक ऋणात्मक संख्या से एक ऋणात्मक संख्या का घटाव :
- नियम – एक ऋणात्मक संख्या को को दूसरी ऋणात्मक संख्या से घटाना, निरपेक्ष मानों को जोड़ने और ऋणात्मक चिह्न को रखने के समान है।
- बेला की इमारत-यदि बेला भूतल से 3 तल नीचे है (-3) और 2 तल ऊपर जाती है, तो वह भूतल से 1 तल नीचे (- 1) पहुँच जाती है।
- संख्या रेखा -2 घटाकर 3 से 1 तक जाना।
उदाहरण- – 3 – 2 (− 2) = -1
2. प्रत्येक नियम के लिए स्वयं के उदाहरण दीजिए।
उत्तर: 1. धनात्मक संख्याओं का योग
उदाहरण – 7 + 4 = 11
बेला की इमारत – 7वें तल से शुरू होकर 4 तल ऊपर 11वें तल तक जाएगी।
2. ऋणात्मक संख्याओं का योग
उदाहरण- −6 + (−3) = -9
बेला की इमारत – भूतल से 6 तल नीचे से शुरू होकर 3 तल नीचे 9वें तल तक जाती है।
3. एक धनात्मक और एक ऋणात्मक संख्या का योग:
उदाहरण: 8 + (−5) = 3
बेला की इमारत – 8वें तल से शुरू होकर 5 तल नीचे तीसरे तल तक जाएगी।
4. एक ऋणात्मक संख्या से एक धनात्मक संख्या का घटाव
उदाहरण- -4 −3 = −7
बेला की इमारत – भूतल से 4 तल नीचे से शुरू होकर 3 तल नीचे जमीन से 7वें तल नीचे तक जाती है।
5. एक धनात्मक संख्या से एक ऋणात्मक संख्या का घटाव :
उदाहरण- 5 – (- 2) = 7
बेला की इमारत – 5वें तल से शुरू होकर 2 तल ऊपर 7वें तल तक जाएगी।
6. एक ऋणात्मक संख्या से एक ऋणात्मक संख्या का घटाव:
उदाहरण- -5 – (- 3) = -2
बेला की इमारत – जमीन से 5 तल नीचे सँ शुरू होकर 3 तल ऊपर भूतल से 2 तल नीचे तक जाती है।


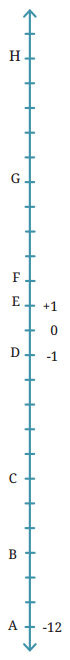

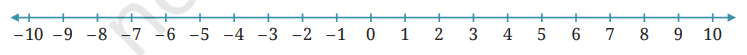



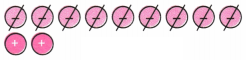















Leave a Reply