Question Answer For All Chapters – गणित प्रकाश Class 6th
संख्याओ का खेल
आइए, पता लगाएँ (Page 57, 58)
1. नीचे दी गई सारणी में महाकोष्ठ को रंगीन या चिह्नित कीजिए।
उत्तर:
2. नीचे दी गई सारणी को चार अंकों वाली संख्याओं से इस प्रकार भरिए कि प्रत्येक रंगीन कोष्ठ ही महाकोष्ठ हो।
उत्तर:
3. नीचे दी गई सारणी को इस प्रकार भरिए कि हमें अधिक से अधिक महाकोष्ठ प्राप्त हों। बिना दोहराए 100 से 1000 के बीच की संख्याओं का उपयोग कीजिए।
उत्तर:
4. उपरोक्त सारणी में 9 संख्याओं में से कितने महाकोष्ठ हैं?
उत्तर: उपरोक्त सारणी में 5 महाकोष्ठ हैं। – 999, 650, 654, 743, 834
5. भिन्न संख्याओं के कोष्ठों में कितने महाकोष्ठ संभव हैं? क्या आपको इनमें कोई पैटर्न दिखाई देता है? दी गई सारणी को भरने का वह कौन सा तरीका होगा जिससे हमें अधिक से अधिक महाकोष्ठ प्राप्त हों? ढूँढ़िए और अपनी योजना को साझा कीजिए।
उत्तर: यदि कोई n विषम (odd) कोष्ठ हों, तो महाकोष्ठों की संख्या = n+1/2
यदि कोई n सम (even) कोष्ठ हों, तो महाकोष्ठों की संख्या = n/2
हाँ, इसमें एक पैटर्न है। वैकल्पिक कोष्ठ महाकोष्ठ हो सकते हैं।
दी गई सारणी को इस प्रकार भरें ताकि अधिकतम महाकोष्ठ प्राप्त हों:
- पहला कोष्ठ महाकोष्ठ बनाएँ। उसके बाद हर वैकल्पिक कोष्ठ को महाकोष्ठ बनाएँ।
- कोई भी दो लगातार कोष्ठ महाकोष्ठ नहीं हो सकते, सिवाय 4 कोष्ठों के मामले में, जहाँ पहला और चौथा कोष्ठ महाकोष्ठ हो सकते हैं।
6. क्या आप संख्याओं को बिना दोहराए एक रिक्त महाकोष्ठ सारणी को इस प्रकार भर सकते हैं कि उसमें कोई महाकोष्ठ न हो? क्यों या क्यों नहीं?
उत्तर: नहीं, यह संभव नहीं है। बिना संख्याओं को दोहराए एक महाकोष्ठ सारणी में कोई महाकोष्ठ न होना संभव नहीं है।
कारण: सबसे बड़ी संख्या हमेशा अपने सभी पड़ोसियों से बड़ी होगी, इसलिए वह महाकोष्ठ बन जाएगी।
7. क्या एक सारणी में सबसे बड़ी संख्या वाला कोष्ठ, हमेशा महाकोष्ठ होगा? क्या एक सारणी में सबसे छोटी संख्या वाला कोष्ठ एक महाकोष्ठ हो सकता है? क्यों या क्यों नहीं?
उत्तर: नहीं, यदि सबसे बड़ी संख्या वाला कोष्ठ अपने सभी पड़ोसी कोष्ठों से बड़ा है, तभी वह महाकोष्ठ होगा।
लेकिन अगर उसके किसी पड़ोसी में उससे भी बड़ी संख्या हो, तो वह महाकोष्ठ नहीं बनेगा।
इसी तरह, सबसे छोटी संख्या कभी भी महाकोष्ठ नहीं हो सकती।
महाकोष्ठ बनने के लिए किसी कोष्ठ का अपने सभी पड़ोसी कोष्ठों से बड़ा होना आवश्यक है।
चूंकि वह संख्या सबसे छोटी है, वह किसी भी पड़ोसी संख्या से बड़ी नहीं हो सकती, इसलिए वह महाकोष्ठ नहीं बन सकती।
8. एक सारणी को इस प्रकार से भरिए कि दूसरी सबसे बड़ी संख्या वाला कोष्ठ, महाकोष्ठ न हो।
उत्तर:
| 800 | 751 | 500 | 550 | 450 | 300 | 200 | 250 |
यहाँ, दूसरी सबसे बड़ी संख्या 751 एक महाकोष्ठ नहीं है।
9. एक सारणी को इस प्रकार से भरिए कि दूसरी सबसे बड़ी संख्या वाला कोष्ठ, महाकोष्ठ न हो, लेकिन दूसरी सबसे छोटी संख्या वाला कोष्ठ एक महाकोष्ठ हो? क्या यह संभव है?
उत्तर:
| 800 | 751 | 500 | 550 | 450 | 300 | 200 | 250 |
हाँ, यहाँ, दूसरी सबसे छोटी संख्या 250 एक महाकोष्ठ है, परंतु दूसरी सबसे बड़ी संख्या 751 एक महाकोष्ठ नहीं है।
पृष्ठ 58-59
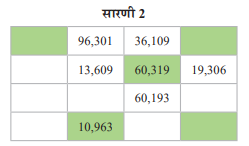
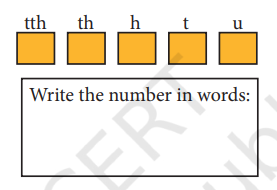
1, 0, 6, 3 और 9 अंकों का किसी भी क्रम में प्रयोग करके पाँच अंकों की संख्याएँ बनाइए और सारणी 2 को पूरा कीजिए। केवल रंगीन कोष्ठ में समीपवर्ती कोष्ठों की संख्याओं से बड़ी होनी चाहिए।
सारणी में सबसे बड़ी संख्या __________________ है।
सारणी में सबसे छोटी सम संख्या __________________ है।
सारणी में 50,000 से बड़ी सबसे छोटी संख्या __________________ है।
उत्तर:
| 96,310 | 96,301 | 36,109 | 63,109 |
| 10,369 | 13,609 | 60,319 | 19,306 |
| 10,936 | 36,910 | 60,193 | 39,106 |
| 10,369 | 10,963 | 10,639 | 39,610 |
सारणी में सबसे बड़ी संख्या 96,310 है।
सारणी में सबसे छोटी सम संख्या 10,936 है।
सारणी में 50,000 से बड़ी सबसे छोटी संख्या 60,193 है।
आइए, पता लगाएँ (Page 59)
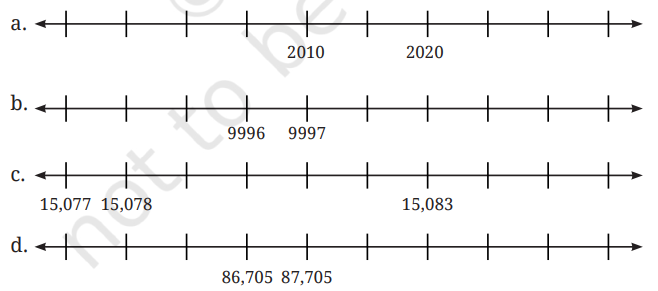
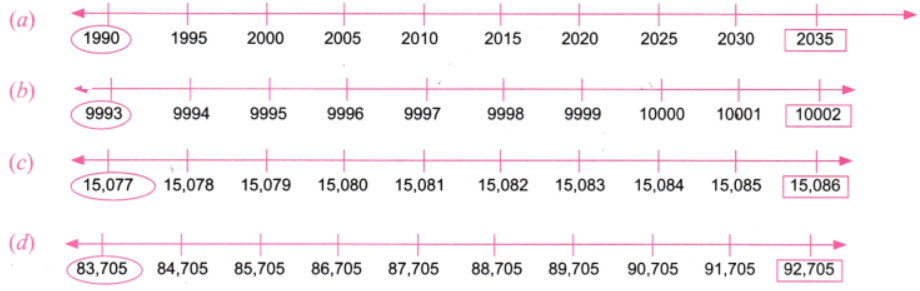
नीचे दी गई संख्या रेखा पर चिह्नित संख्या को पहचान कर, नीचे दिए गए संख्या अनुक्रमों को पूरा कीजिए।
उपरोक्त अनुक्रमों में सबसे छोटी संख्या पर गोला लगाइए तथा सबसे बड़ी संख्या पर बॉक्स बनाइए।
उत्तर:
आइए, पता लगाएँ (Page 60)
1. अंकों का योग 14
(a) अन्य संख्याएँ लिखिए जिनके अंकों का योगफल 14 है।
(b) वह सबसे छोटी संख्या कौन-सी है, जिसके अंकों का योगफल 14 है?
(c) 5 अंकों की वह सबसे बड़ी संख्या कौन-सी है, जिसके अंकों का योगफल 14 है?
(d) वह बड़ी से बड़ी कौन-सी संख्या बनाई जा सकती है, जिसके अंकों का योगफल 14 है? क्या आप इससे भी बड़ी संख्या बता सकतें हैं?
उत्तर: (a) अंक योग 14 वाली संख्याएँ59, 68, 77, 86, 95, 149, 158, 167, 176, 185, 194, 239, 248, 257, 266, 275, 281 इत्यादि हैं।
(b) ऐसी सबसे छोटी संख्या 14 = 59 है।
(c) अंक योग 14 वाली 5 अंकों की सबसे बड़ी संख्या 95,000 है।
(d) अंक योग 14 वाली हम कितने भी अंकों की संख्या बना सकते हैं। उदाहरणार्थ, 950000, 9500000, 95000000, इत्यादि। इसका कोई अंत नहीं है।
2. 40 से 70 तक की सभी संख्याओं के अंकों का योगफल ज्ञात कीजिए। अपने अवलोकन को कक्षा के साथ साझा कीजिए।
उत्तर:
| Number | Digit Sum | Number | Digit Sum |
|---|---|---|---|
| 40 | 4 | 55 | 10 |
| 41 | 5 | 56 | 11 |
| 42 | 6 | 57 | 12 |
| 43 | 7 | 58 | 13 |
| 44 | 8 | 59 | 14 |
| 45 | 9 | 60 | 6 |
| 46 | 10 | 61 | 7 |
| 47 | 11 | 62 | 8 |
| 48 | 12 | 63 | 9 |
| 49 | 13 | 64 | 10 |
| 50 | 5 | 65 | 11 |
| 51 | 6 | 66 | 12 |
| 52 | 7 | 67 | 13 |
| 53 | 8 | 68 | 14 |
| 54 | 9 | 69 | 15 |
| 70 | 7 |
3. 3 अंकों की उन संख्याओं का योगफल ज्ञात कीजिए, जिनके अंक क्रमागत (जैसे: 345) हों। क्या आप उनमें एक पैटर्न देखते हैं? क्या यह पैटर्न जारी रहेगा?
उत्तर:
यदि हम संख्याओं को उलटे क्रम में लें, तो अंकों का योग वही रहता है।
हाँ, हमें एक पैटर्न दिखाई देता है।
अर्थात्: (पहली संख्या + 1) × 3 = अंकों का योग
पृष्ठ 61
1 से 100 तक की संख्याओं में, अंक ‘7’ कितनी बार आएगा? 1 से 1000 तक की संख्याओं में, अंक ‘7’ कितनी बार आएगा।
उत्तर: (i) संख्याओं 1-100 में अंक ‘7’ संख्याओं 7, 17, 27, 37, 47, 57, 67, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 87 और 97 में आएगा। अतः यह 20 बार आएगा।
(ii) संख्याओं को 1 से 1000 तक लिखते समय अंक 7 कुल 300 बार लिखा जाएगा।
पृष्ठ 61
इन अंकों की सहायता से बनने वाली सभी तीन अंकों की पैलिंड्रोमिक संख्याएँ लिखिए।
उत्तर: अन्य संभव 3 अंकीय संख्याएँ 111, 333, 131, 212, 232, 323 है।
पृष्ठ 62 पहेली
मैं 5 अंकों का एक पैलिंड्रोम हूँ।
मैं एक विषम संख्या हूँ।
मेरा दहाई का अंक, इकाई के अंक से दो गुना है।
मेरा सैकड़े का अंक, बहाई के अंक से दो गुना है।
मैं कौन हूँ? _______________________
उत्तर: 12421
पृष्ठ 63
4 अंकों की कोई अन्य संख्या लेकर इन चरणों का अनुसरण करके प्रयास कीजिए। पता लगाइए कि क्या होता है? अपनेमित्रों के साथ जाँच कीजिए कि उन्हें क्या संख्या प्राप्त हुई?
उत्तर: उदाहरण के लिए, 4-अंकीय संख्या 3524 को लें:
अवरोही क्रम में रखें: 5432 (A)
आरोही क्रम में रखें: 2345 (B)
घटाएँ: 5432 – 2345 = 3087 (C)
अब 3087 के साथ यही प्रक्रिया दोहराएँ:
अवरोही क्रम: 8730
आरोही क्रम: 0378
घटाएँ: 8730 – 0378 = 8352
फिर से दोहराएँ:
अवरोही क्रम: 8532
आरोही क्रम: 2358
घटाएँ: 8532 – 2358 = 6174
6174 प्राप्त होता है, जिसे कपरेकर स्थिरांक (Kaprekar Constant) कहा जाता है।
आइए, पता लगाएँ (Page 64)
प्रतिभा अंकों ‘4’, ‘7’, ‘3’ और ‘2’ का उपयोग करके 4 अंकों की सबसे बड़ी संख्या 7432 तथा सबसे छोटी संख्या 2347 बनाती है। इन दोनों संख्याओं का अंतर 7432 – 2347 = 5085 है। इन दोनों संख्याओं का योगफल 9779 है। निम्नलिखित कथन को हल करने के लिए 4 अंकों को चुनिए-
(a) सबसे बड़ी तथा सबसे छोटी संख्या का अंतर 5085 से अधिक हो।
(b) सबसे बड़ी तथा सबसे छोटी संख्या का अंतर 5085 से कम हो।
(c) सबसे बड़ी तथा सबसे छोटी संख्या का योगफल 9779 से अधिक हो।
(d) सबसे बड़ी तथा सबसे छोटी संख्या का योगफल 9779 से कम हो।
उत्तर: (a) इसके लिए, हम अंक 4, 8, 3 और 2 लेते हैं। तब, 8432 – 2348 6084 है, जो 5085 से अधिक है।
(b) इसके लिए, हम अंक 4, 6, 3 और 2 लेते हैं। तब, 6432 – 2346 = 4086 है, जो 5085 से कम है।
(c) इसके लिए हम अंक 6, 7, 3 और 2 लेते हैं। तब, 7632 + 2367 = 9999 है, जो 9779 से अधिक है।
(d) इसके लिए, हम अंक 6, 7, 3 और 1 लेते हैं। तब, 7631 + 1367 = 8998 है, जो 9779 से कम है।
2. 5 अंकों के सबसे बड़े तथा सबसे छोटे पैलिंड्रोम (विलोमाक्षर) का योगफल क्या होगा? उनका अंतर क्या होगा?
उत्तर: 5 अंकों का सबसे छोटा पैलिंड्रोम = 10001
5 अंकों का सबसे बड़ा पैलिंड्रोम = 99999
उनका योग = 110000 है।
3. घड़ी में इस समय 10 : 01 बजे हैं। कितने मिनट लगेंगे जब तक की घड़ी अगला पैलिंड्रोम दिखाती है? इस पैलिंड्रोम के बाद आप अगले के बारे में क्या कहेंगे?
उत्तर: 10:01 के बाद अगला पलिंड्रोमिक समय 11:11 है।
10:01 और 11:11 के बीच का अंतर 1 घंटा 10 मिनट है, जो कि 70 मिनट होता है।
11:11 के बाद अगला पलिंड्रोमिक समय 12:21 है।
11:11 और 12:21 के बीच का अंतर भी 1 घंटा 10 मिनट यानी 70 मिनट होता है।
4. संख्या 5683 को कापरेकर स्थिरांक तक पहुँचने की प्रक्रिया में कितने चरण लगेंगे?
उत्तर: संख्या 5683 को कापरेकर स्थिरांक 6174 तक पहुँचने में 7 चरण लगते हैं।
- 8653 – 3568 = 5085
- 8550 – 0558 = 7992
- 9972 – 2799 = 7173
- 7731 – 1377 = 6354
- 6543 – 3456 = 3087
- 8730 – 0378 = 8352
- 8532 – 2358 = 6174
आइए, पता लगाएँ (Page 66)
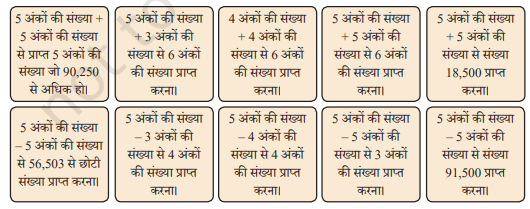
1. नीचे दी गई प्रत्येक स्थिति के लिए जहाँ भी संभव हो, वहाँ एक उदाहरण लिखिए।
क्या आप दी गई सभी स्थितियों के लिए उपयुक्त उदाहरण खोज पाए? यदि नहीं, तो सोचिए और चर्चा कीजिए कि इसका क्या कारण हो सकता है? ऐसे ही कुछ और प्रश्न तैयार कीजिए एवं अपने सहपाठियों को चुनौती बीजिए।
उत्तर: a. 5 अंकों की संख्या + 5 अंकों की संख्या = 5 अंकों की संख्या जो 90,250 से अधिक हो
56789 + 43210 = 99999
b. 5 अंकों की संख्या + 3 अंकों की संख्या = 6 अंकों की संख्या
98521 + 679 = 99100
c. 4 अंकों की संख्या + 4 अंकों की संख्या = 6 अंकों की संख्या
9999 + 9901 = 19900
d. 5 अंकों की संख्या + 5 अंकों की संख्या = 6 अंकों की संख्या प्राप्त करना
54321 + 56789 = 111110
e. 5 अंकों की संख्या + 5 अंकों की संख्या = संख्या 18,500 प्राप्त करना
संभव नहीं, क्योंकि 5 अंकों की सबसे छोटी संख्या 10000 होती है, दो 5 अंकों की संख्या जोड़ने पर 20000 से कम नहीं हो सकता।
f. 5 अंकों की संख्या – 5 अंकों की संख्या = 5 अंकों की संख्या जो 56,503 से छोटी हो
90000 – 40000 = 50000
g. 5 अंकों की संख्या – 3 अंकों की संख्या = 4 अंकों की संख्या प्राप्त करना
10000 – 999 = 9001
h. 5 अंकों की संख्या – 4 अंकों की संख्या = 4 अंकों की संख्या प्राप्त करना
20000 – 9999 = 10001
i. 5 अंकों की संख्या – 3 अंकों की संख्या = 3 अंकों की संख्या प्राप्त करना
10900 – 10001 = 899
j. 5 अंकों की संख्या – 5 अंकों की संख्या = 3 अंकों की संख्या 91,500 प्राप्त करना
संभव नहीं, क्योंकि 91,500 एक 5 अंकों की संख्या है, जबकि परिणाम 3 अंकों की संख्या होना चाहिए। यह विरोधाभास है।
2. हमेशा, कभी-कभी, कभी नहीं?
नीचे कुछ कथन दिए गए हैं। सोचिए, खोजिए और ज्ञात कीजिए कि क्या प्रत्येक कथन ‘हमेशा सत्य है’, ‘केवल कभी-कभी सत्य है’ ‘या कभी सत्य नहीं है’। आप ऐसा क्यों सोचते हैं? अपने तर्क लिखिए और कक्षा में चर्चा कीजिए।
(a) 5 अंकों की संख्या + 5 अंकों की संख्या से प्राप्त होती है, एक 5 अंकों की संख्या।
(b) 4 अंकों की संख्या + 2 अंकों की संख्या से प्राप्त होती है, एक 4 अंकों की संख्या।
(c) 4 अंकों की संख्या + 2 अंकों की संख्या से प्राप्त होती है, एक 6 अंकों की संख्या।
(d) 5 अंकों की संख्या – 5 अंकों की संख्या से प्राप्त होती है, एक 5 अंकों की संख्या।
(e) 5 अंकों की संख्या – 2 अंकों की संख्या से प्राप्त होती है, एक 3 अंकों की संख्या।
उत्तर: (a) केवल कभी-कभी सत्य है। उदाहरणार्थ, 44,443 + 55,554 99,997 एक 5 अंकीय संख्या है तथा 87,250 + 21,319 = 1,08,569 एक 5 अंकीय संख्या नहीं है।
(b) केवल कभी-कभी सत्य है। उदाहरणार्थ, 9,843 + 23 = 9,866 एक 4 अंकीय संख्या है परंतु 9,998 + 21 = 10,019 एक 4 अंकीय संख्या नहीं है।
(c) कभी भी सत्य नहीं है। उदाहरणार्थ, 9999 + 99 = 10,098 जो एक 5 अंकीय संख्या है।
(d) केवल कभी-कभी सत्य है। उदाहरणार्थ, 98,789 – 87,678 = 11,111 एक 5 अंकीय संख्या है, परंतु 99,896 – 97,185 = 2,711 एक 4 अंकीय संख्या है।
(e) कभी भी सत्य नहीं है, क्योंकि 10,000 – 99 = 9,901 एक 3 अंकीय संख्या नहीं है।
पृष्ठ 67-68
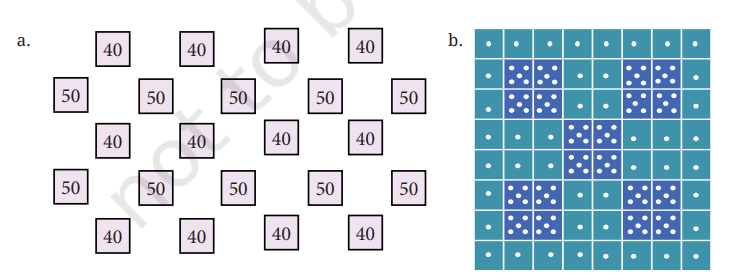
प्रश्न: इन प्रश्नों को हल करने के लिए आपने जिन अलग-अलग विधियों का प्रयोग किया है, उसे कक्षा में साझा कीजिए और चर्चा कीजिए।
उत्तर: (a) योग = 40 × 4 + 50 × 5 + 40 × 4 + 50 × 5 + 40 × 4
= 160 + 250 + 160 + 250 + 160
= 160 × 3 + 250 × 2
= 480 + 500
= 980 है।
(b) योग = 1 × 8 + 1 × 4 + 5 × 4 + 1 × 4 + 5 × 4 + 1 × 6 + 5 × 2 + 1 × 6 + 5 × 2 + 1 × 4 + 5 × 4 + 1 × 4 + 5 × 4 + 1 × 8
= 8 + 4 + 20 + 4 + 20 + 6 + 10 + 6 + 10 + 4 + 20 + 4 + 20 + 8
= 8 × 2 + 4 × 4 + 20 × 4 + 6 × 2 + 10 × 2
= 16 + 16 + 80 + 12 + 20
= 32 + 80 + 32
= 32 × 2 + 80
= 64 + 80
= 144 है।
(c) योग = 32 × 32 + 64 × 16
= 1024 + 1024
= 1024 × 2
= 2048 है।
(d) योग = 3 × 7 + 4 × 6 + 3 + 4 × 6 + 3 + 4 × 6 + 3 + 3 × 7
= 21 + 24 + 3 × 3 + 24 + 24 + 21
= 21 × 2 + 24 × 3 + 9
= 42 + 72 + 9
= 114 + 9
= 123 है।
या योग हो सकता है: 18 × 6 + 3 × 5 = 108 + 15 = 123
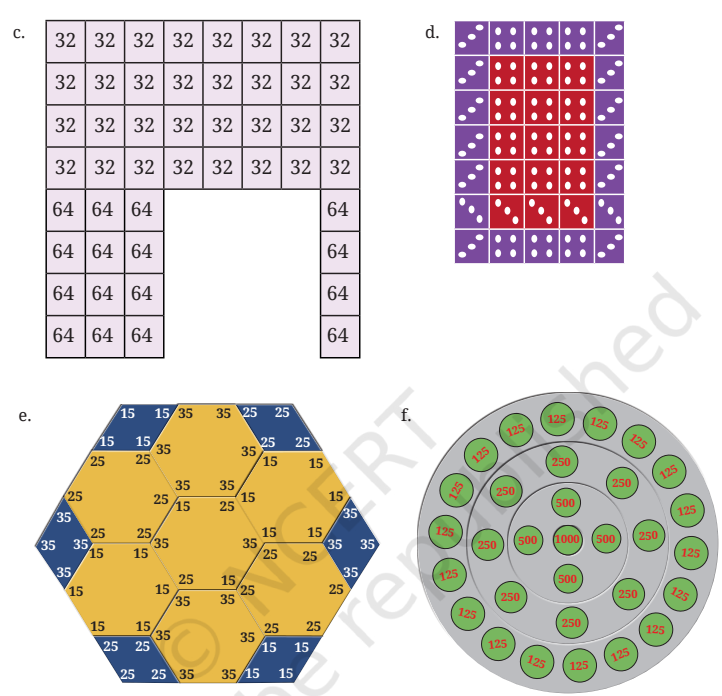
(e) योग = 15 × 4 + 35 × 6 + 25 × 4 + 25 × 6 + 35 × 4 + 15 × 6 + 25 × 4 + 35 × 6 + 15 × 4 + 25 × 6 + 35 × 4 + 15 × 6 + 15 × 1 + 25 × 1 + 35 × 2 + 25 × 1 + 15 × 1
= 15 × 22 + 35 × 22 + 25 × 22
= 330 + 770 + 550
= 1650
(f) योग = 1000 × 1 + 500 × 4 + 250 × 8 + 125 × 18
= 1000 + 2000 + 2000 + 2250
= 7250 है।
उत्तर का आकलन कीजिए (Page 70,71)
30 सेकंड के अंदर अनुमान लगाने का प्रयास कीजिए। अपने अनुमान को अपने दोस्तों के साथ जाँचिए।
1. आपकी गणित की पाठ्यपुस्तक में शब्दों की संख्या:
(a) 5000 से अधिक
(b) 5000 से कम
उत्तर: मेरी गणित पाठ्यपुस्तक में शब्दों की संख्या: 5000 से अधिक है क्योंकि कक्षा 6 की अधिकांश पुस्तकों में अनेक स्पष्टीकरण, अभ्यास प्रश्न और उदाहरण होते हैं, जिससे कुल शब्दों की संख्या संभवतः 5000 से अधिक हो जाती है।
2. आपके विद्यालय में बस द्वारा आने वाले विद्यार्थियों की संख्या:
(a) 200 से अधिक
(b) 200 से कम
उत्तर: मेरे विद्यालय में बस से यात्रा करने वाले छात्रों की संख्या: 200 से अधिक।
क्योंकि एक बड़े विद्यालय में, विशेष रूप से जब वह व्यापक क्षेत्र को सेवा देता है, तो कई छात्र बसों पर निर्भर होते हैं।
3. रोशन 5 व्यक्तियों के लिए फ्रूट कस्टर्ड बनाने के लिए दूध और 3 प्रकार के फल खरीदना चाहता है। उसका अनुमान है कि फ्रूट कस्टर्ड बनाने की लागत ₹ 100 है। क्या आप उससे सहमत हैं? क्यों या क्यों नहीं?
उत्तर: नहीं, मैं सहमत नहीं हूँ। इसका कारण यह है कि 5 व्यक्तियों के लिए कस्टर्ड बनाने के लिए आवश्यक केवल दूध या फलों की पृथक-पृथक लागत ही ₹ 100 से अधिक होगी। अतः उसका आकलन सही नहीं है।
4. गांधीनगर (गुजरात में) और कोहिमा (नागालैंड में) के बीच की दूरी का आकलन कीजिए।
[संकेत- इन शहरों का पता लगाने के लिए भारत के मानचित्र को देखिए।]
उत्तर: दूरी लगभग 2500 से 3000 किलोमीटर है।
ये दोनों शहर (गांधीनगर और कोहिमा) भारत के विपरीत छोरों पर स्थित हैं, जिससे यह एक लंबी दूरी की यात्रा बनती है।
5. शीतल कक्षा 6 में है और कहती है कि उसने विद्यालय में आज तक लगभग 13,000 घंटे व्यतीत किए हैं? क्या आप उससे सहमत हैं? क्यों या क्यों नहीं?
उत्तर: नहीं, संभवतः लगभग 7,200 घंटे होंगे।
औसतन एक स्कूल दिवस 6 घंटे का होता है और एक वर्ष में लगभग 200 स्कूल दिवस होते हैं।
6 वर्षों में कुल समय = 6 × 200 × 6 = 7,200 घंटे के करीब होता है।
6. पुराने समय में यातायात के साधन उपलब्ध नहीं होने के कारण लोग लंबी दूरी पैदल चलकर तय करते थे। माना आप अपनी सामान्य गति से चलते हैं। आपको निम्न स्थानों से जाने में लगभग कितना समय लगेगा?
(a) आपके वर्तमान स्थान से आपके आसपास के एक पसंदीदा स्थान तक
(b) आपके वर्तमान स्थान से किसी पड़ोसी राज्य की राजधानी तक
(c) भारत के सुदूर दक्षिणी बिंदु से भारत के सुदूर उत्तरी बिंदु तक
उत्तर: (a) यदि दूरी लगभग 2–3 किमी हो, तो समय =
25–35 मिनट
(b) मान लें दूरी लगभग 300 किमी हो, तो:
प्रतिदिन 8 घंटे चलें = 40 किमी/दिन
समय = 7–8 दिन
(c) भारत के सुदूर उत्तरी बिंदु (सियाचिन क्षेत्र) तक
कुल दूरी लगभग 3,500–4,000 किमी
प्रतिदिन 40 किमी पैदल यात्रा करने पर:
समय = लगभग 90–100 दिन
आइए, पता लगाएँ (Page 72, 73)
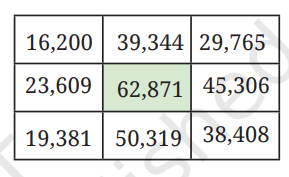
1. यहाँ इस ग्रिड में केवल एक महाकोष्ठ है (अपने पड़ोस की सभी संख्याओं में बड़ी संख्या)। यदि आप इनमें से किसी एक संख्या के दो अंकों की अदला-बदली करते हैं, तो यहाँ 4 महाकोष्ठ बन जाते हैं। जानिए कि कौन-से अंकों की अदला-बदली की जानी चाहिए।
उत्तर: यदि हम मध्य संख्या 62,871 की पहली और अंतिम अंक की अदल-बदल करें, तो हमें वांछित परिणाम प्राप्त होता है।
| 16,200 | 39,344 | 29,765 |
| 23,609 | 21,876 | 45,306 |
| 19,381 | 50,319 | 38,408 |
2. अपने जन्म वर्ष से शुरू करके आप कितने चरण में कापरेकर स्थिरांक पर पहुँच जाएँगे?
उत्तर:
अपने जन्म वर्ष (उदाहरण के लिए: 2008) से शुरू करके कपरेकर स्थिरांक 6174 तक पहुँचने के लिए आपको निम्नलिखित चरणों का पालन करना होगा:
चरण 1:
2008 →
अवरोही क्रम: 8200
आरोही क्रम: 0028
8200 – 0028 = 8172
चरण 2:
8172 →
अवरोही क्रम: 8721
आरोही क्रम: 1278
8721 – 1278 = 7443
चरण 3:
7443 →
अवरोही क्रम: 7443
आरोही क्रम: 3447
7443 – 3447 = 3996
चरण 4:
3996 →
अवरोही क्रम: 9963
आरोही क्रम: 3699
9963 – 3699 = 6264
चरण 5:
6264 →
अवरोही क्रम: 6642
आरोही क्रम: 2466
6642 – 2466 = 4176
चरण 6:
4176 →
अवरोही क्रम: 7641
आरोही क्रम: 1467
7641 – 1467 = 6174
3. हम 35,000 और 75,000 के बीच पाँच अंकों की संख्याओं का वह समूह है, जिसके सभी अंक विषम हैं। हमारे समूह की सबसे बड़ी संख्या कौन-सी है? हमारे समूह की सबसे छोटी संख्या कौन-सी है? हम में से कौन-सी संख्या 50,000 के अत्यधिक निकट है?
उत्तर: सबसे बड़ी संख्या = 73,999 है।
सबसे छोटी संख्या = 35,111 है।
50,000 के निकटतम संख्या = 51,111 है।
4. आकलन कीजिए कि आपको वर्ष में सप्ताहांतों (Weakends), त्योहारों और छुट्टियों को मिलाकर कुल कितनी छुट्टियाँ मिलती हैं। अब अपनी छुट्टियों की सही संख्या का पता लगाइए और देखिए कि सही संख्या आपके आकलन के कितना समीप है।
उत्तर: एक वर्ष में छुट्टियाँ
सप्ताहांत (शनिवार-रविवार): 104 दिन
गर्मी की छुट्टियाँ: 50 दिन
सर्दी की छुट्टियाँ: 12 दिन
त्योहारों की छुट्टियाँ: 12 दिन
सरकारी अवकाश: 4 दिन
कुल अनुमानित छुट्टियाँ = 104 + 50 + 12 + 12 + 4 = 182 दिन
5. एक जग, एक बाल्टी और एक छत पर रखी टंकी की क्षमता का लीटर में आकलन कीजिए।
उत्तर: नीचे एक जग, एक बाल्टी और एक छत पर रखी टंकी की औसत क्षमता का अनुमान (आकलन) लीटर में दिया गया है:
- एक जग (Jug): लगभग 1 लीटर
- एक बाल्टी (Bucket): लगभग 15–20 लीटर
- छत पर रखी टंकी (Overhead Tank): लगभग 500–1000 लीटर (घरेलू टंकी)
या
1000–2000 लीटर (थोड़ी बड़ी टंकी)
6. एक 5 अंकों की संख्या तथा दो 3 अंकों की संख्याएँ इस प्रकार लिखिए कि उनका योगफल 18,670 हो।
उत्तर: 18,400 + 130 + 140 = 18,670 है।
7. 210 और 390 के बीच एक संख्या चुनिए। अनुच्छेद 3.9 में दिए गए संख्या पैटर्न के समान एक पैटर्न निर्मित कीजिए, जिसमें यह चुनी गई संख्या योगफल हो।
उत्तर:
सरल जोड़ का पैटर्न
हम एक सरल जोड़ का पैटर्न बार-बार आने वाली संख्याओं की श्रृंखला से बना सकते हैं:
40 + 40 + 40 + 50 + 50 + 50 + 30 = 300
पैटर्न: 40 को 3 बार, 50 को 3 बार और अंत में 30
40 + 40 + 40 = 120
50 + 50 + 50 = 150
120 + 150 + 30 = 300
एक अन्य तरीका:
50 + 50 + 50 + 50 + 50 + 50 = 300
इस पैटर्न में 50 को 6 बार दोहराया गया है ताकि योग 300 आए।
हम पैटर्न को इस प्रकार भी बदल सकते हैं:
40 + 60 + 50 + 70 + 30 + 50 = 300
इसमें अलग-अलग संख्याओं का प्रयोग करके योगफल 300 प्राप्त किया गया है।
8. अध्याय 1 की सारणी 1 से 2 की घात का अनुक्रम याद कीजिए। इस अनुक्रम में शुरू की सभी संख्याओं के लिए कोलाट्ज अनुमान सही क्यों है?
उत्तर: 2 की घात वाले संख्याओं का क्रम है:
1, 2, 4, 8, 16, 32, 64
अब कोलाट्ज Conjecture के अनुसार संख्या 64 को लें:
- 64 सम है, 2 से भाग दें → 64 ÷ 2 = 32
- 32 सम है, 2 से भाग दें → 32 ÷ 2 = 16
- 16 सम है, 2 से भाग दें → 16 ÷ 2 = 8
- 8 सम है, 2 से भाग दें → 8 ÷ 2 = 4
- 4 सम है, 2 से भाग दें → 4 ÷ 2 = 2
- 2 सम है, 2 से भाग दें → 2 ÷ 2 = 1
इस प्रकार, Collatz अनुमान (Conjecture) 2 की घात वाली सभी संख्याओं के लिए सत्य है।
क्योंकि ये सभी संख्याएँ सम होती हैं, और Collatz नियम के अनुसार हर सम संख्या को 2 से विभाजित किया जाता है जब तक हम 1 तक नहीं पहुँच जाते।
9. यदि कोई व्यक्ति संख्या 100 से शुरू करता है, तो क्या कोलाट्ज अनुमान लागू होगा, इस विषय की जाँच कीजिए।
उत्तर: आइए संख्या 100 से शुरू करके देखें कि क्या कोलाट्ज अनुमान (Collatz Conjecture) लागू होता है या नहीं।
नियम:
- यदि संख्या सम (even) है → 2 से भाग दें
- यदि संख्या विषम (odd) है → (3 × संख्या) + 1 करें
चरण दर चरण:
- 100 (सम) → 100 ÷ 2 = 50
- 50 (सम) → 50 ÷ 2 = 25
- 25 (विषम) → 3×25 + 1 = 76
- 76 (सम) → 76 ÷ 2 = 38
- 38 (सम) → 38 ÷ 2 = 19
- 19 (विषम) → 3×19 + 1 = 58
- 58 (सम) → 58 ÷ 2 = 29
- 29 (विषम) → 3×29 + 1 = 88
- 88 (सम) → 88 ÷ 2 = 44
- 44 (सम) → 44 ÷ 2 = 22
- 22 (सम) → 22 ÷ 2 = 11
- 11 (विषम) → 3×11 + 1 = 34
- 34 (सम) → 34 ÷ 2 = 17
- 17 (विषम) → 3×17 + 1 = 52
- 52 (सम) → 52 ÷ 2 = 26
- 26 (सम) → 26 ÷ 2 = 13
- 13 (विषम) → 3×13 + 1 = 40
- 40 (सम) → 40 ÷ 2 = 20
- 20 (सम) → 20 ÷ 2 = 10
- 10 (सम) → 10 ÷ 2 = 5
- 5 (विषम) → 3×5 + 1 = 16
- 16 → 8 → 4 → 2 → 1
हाँ, संख्या 100 से शुरू करने पर Collatz अनुमान लागू होता है और अंततः 1 पर पहुँच जाता है।
इसलिए, कोलाट्ज अनुमान संख्या 100 के लिए सत्य है।
10. शून्य से प्रारंभ करते हुए खिलाड़ी बारी-बारी से 1 और 3 के बीच संख्या को जोड़ता है, जो व्यक्ति 22 पर पहले पहुँचेगा, वह विजयी होगा। अब जीतने की युक्ति क्या होगी?
उत्तर: इस खेल में, जीतने वाले के लिए जीतने की युक्ति यह है कि वह ऐसी संख्या बोले जिसे जोड़ने पर 2 का एक गुणज (20 के अतिरिक्त) प्राप्त हो, क्योंकि 2 × 11 = 22 है और 22 ही 2 का अगला गुणज है।







Leave a Reply