Question Answer For All Chapters – गणित प्रकाश Class 6th
परिमाप और क्षेत्रफल
आइए, पता लगाएँ (Page 132)
1. लुप्त पदों को ज्ञात कीजिए-
(a) आयत का परिमाप = 14 सेमी; चौड़ाई = 2 सेमी; लंबाई = __________?
(b) वर्ग का परिमाप = एक भुजा की लंबाई 20 सेमी = __________?
(c) आयत का परिमाप = लंबाई 12 मी. = चौड़ाई 3 मी = __________?
उत्तर: a. परिमाप = 14 सेमी, चौड़ाई = 2 सेमी
लंबाई = (14 ÷ 2) – 2 = 7 – 2 = 5 सेमी
b. परिमाप = 20 सेमी
एक भुजा = 20 ÷ 4 = 5 सेमी
c. परिमाप = 12 मी, लंबाई = 3 मी
breadth = (12 ÷ 2) – 3 = 6 – 3 = 3 मी
2. तार के टुकड़े का प्रयोग करके एक आयत बनाया गया है जिसकी भुजाओं की लंबाइयाँ 5 सेमी और 3 सेमी है। यदि तार को सीधा करके एक वर्ग बनाया जाए, तब वर्ग की एक भुजा की लंबाई क्या होगी?
उत्तर: आयत का परिमाप = 2 × (5+3) = 16 सेमी
अब, वर्ग का परिमाप भी = 16 सेमी
भुजा = 16 ÷ 4 = 4 सेमी
3. यदि एक त्रिभुज का परिमाप 55 सेमी है और दो भुजाओं की लंबाइयाँ क्रमशः 20 सेमी और 14 सेमी हैं, तो तीसरी भुजा की लंबाई ज्ञात कीजिए।
उत्तर: तीसरी भुजा की लंबाई = परिमाप – त्रिभुज की दो भुजाओं की लंबाइयों का योग
तीसरी भुजा = 55 – (20+14) = 21 सेमी
4. एक आयताकार पार्क जिसकी लंबाई 150 मी और चौड़ाई 120 मी है, पार्क के चारों ओर ₹ 40 प्रति मीटर की दर से बाड़ लगाने का व्यय ज्ञात कीजिए।
उत्तर: आयताकार पार्क का परिमाप = 2(लंबाई + चौड़ाई)
2 × (150+120) = 540 मी
लागत = 540 × ₹40 = ₹21,600
5. एक धागे के टुकड़े की लंबाई 36 सेमी है। प्रत्येक भुजा की लंबाई क्या होगी, यदि इस धागे से बनाया जाता है-
(a) एक वर्ग
(b) एक त्रिभुज जिसकी सभी भुजाएँ समान लंबाई की हों, और
(e) एक सम षट्भुज (छः भुजाओं वाली बंद आकृति जिसकी सभी भुजाएँ समान लंबाई की हों)?
उत्तर: 36 सेमी लम्बी रस्सी:
a. वर्ग: एक भुजा = 36 ÷ 4 = 9 सेमी
b. समभुज त्रिभुज: एक भुजा = 36 ÷ 3 = 12 सेमी
c. सम षट्भुज एक भुजा = 36 ÷ 6 = 6 सेमी
6. एक किसान के आयताकार भूखंड की लंबाई तथा चौड़ाई क्रमश: 230 मी तथा 160 मी है। वह भूखंड के चारों ओर रस्सी द्वारा तीन पूरे चक्कर की बाड़ बनाना चाहता है। जैसा कि पाठ्यपुस्तक में दिए गए चित्र में दिखाया गया है। किसान के द्वारा प्रयोग की गई रस्सी की कुल लंबाई ज्ञात कीजिए।
उत्तर: चरण 1: एक चक्कर का परिमाप निकालना
परिमाप का सूत्र होता है:
परिमाप = 2 × (लंबाई + चौड़ाई)
तो, परिमाप = 2 × (230+160) = 2×390 = 780 मीटर
चरण 2: तीन चक्करों के लिए कुल लंबाई
कुल रस्सी की लंबाई=3×780 = 2340 मीटर
आइए पता लगाएँ (Page 133-134)
1. अक्षी द्वारा 5 चक्करों में तय की गई कुल दूरी ज्ञात कीजिए।
उत्तर: एक चक्कर का परिमाप (बाहरी पथ)
परिमाप = 2×(लंबाई+चौड़ाई) = 2×(70+40) = 2×110=220 मीटर
5 चक्करों की कुल दूरी
अतः कुल दूरी = 5×220 = 1100 मीटर
2. तोशी द्वारा 7 चक्करों में तय की गई कुल दूरी ज्ञात कीजिए। अक्षी और तोशी में से किसने अधिक दूरी तय की?
उत्तर: एक चक्कर का परिमाप (भीतरी पथ)
परिमाप=2×(60+30)=2×90=180मीटर
7 चक्करों की कुल दूरी
अतः कुल दूरी=7×180 = 1260मीटर
आइए पता लगाएँ (Page 138)
1. 25 मी लंबे आयताकार बाग का क्षेत्रफल 300 वर्ग मी है। इस बाग की चौड़ाई क्या है?
उत्तर: क्षेत्रफल=लंबाई×चौड़ाई
300 = 25×चौड़ाई
अब, चौड़ाई = चौड़ाई= \(\frac{300}{5}\) = 12 मीटर
2. 8 रुपये प्रति 100 वर्ग मी की दर से 500 मी लंबे और 200 मी चौड़े आयताकार भूखंड पर टाइल लगाने की लागत क्या होगी?
उत्तर: क्षेत्रफल निकालना, क्षेत्रफल=लंबाई×चौड़ाई=500×200=100000 वर्ग मीटर
टाइल लगाने की कुल लागत, दर = ₹8 प्रति 100 वर्ग मीटर
लागत = \(\frac{100000}{100}\) = 1000×8 = ₹8000
3. एक आयताकार नारियल वाटिका 100 मी लंबी और 50 मी चौड़ी है। यदि प्रत्येक नारियल के पेड़ के लिए 25 वर्ग मी जगह चाहिए, तो इस वाटिका में अधिकतम कितने पेड़ लगाए जा सकते हैं?
उत्तर: वाटिका का कुल क्षेत्रफल = 100×50 = 5000 वर्ग मीटर
अधिकतम पेड़ों की संख्या = \(\frac{500}{25}\) = 200
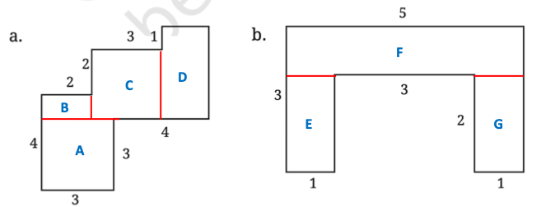
4. नीचे दी गई आकृतियों को आयताकार भागों में बाँटकर, उनके क्षेत्रफल ज्ञात कीजिए (सभी माप मीटर में दिए गए हैं)।
उत्तर:
पहली आकृति का क्षेत्रफल = (3 × 3 + 7 × 1 + 5 × 2 + 2 × 1 ) वर्ग मी
= (9 + 7 + 10 + 2) वर्ग मी = 28 वर्ग मी है।
दूसरी आकृति का क्षेत्रफल = (3 × 1 + 3 × 1 + 3 × 1 ) वर्ग मी = 9 वर्ग मी है।
आइए पता लगाएँ (Page – 139)
आपकी पाठ्यपुस्तक के अंत में दिए गए टैनग्राम के टुकड़े काटिए।
1. खोजिए और पता लगाइए कि कितने टुकड़ों का क्षेत्रफल एक समान है।
उत्तर: टुकड़ों A और B के समान क्षेत्रफल हैं। साथ ही, टुकड़ों C और E के भी समान क्षेत्रफल है।
2. आकार D, आकार C की तुलना में कितने गुना बड़ा है? C, D और E में क्या संबंध है?
उत्तर: आकार D, आकार C से 2 गुना बड़ा है।
संबंध = D = C+E
यानी, आकार D का क्षेत्रफल = आकार C और आकार E के क्षेत्रफल का योग है।
3. किस आकार का क्षेत्रफल अधिक है- आकार D या आकार F? अपने उत्तर का कारण बताइए।
उत्तर: आकार D और आकार F — दोनों का क्षेत्रफल बराबर है।
4. किस आकार का क्षेत्रफल अधिक है- आकार F या G का? अपने उत्तर का कारण बताइए।
उत्तर: आकार F और G के क्षेत्रफल बराबर हैं।
5. आकार G की तुलना में आकार A का क्षेत्रफल कितना है? क्या यह दोगुना बड़ा है? क्या यह चार गुना बड़ा है?
[संकेत : टैनग्राम के टुकड़ों को काटने के पश्चात् एक टुकड़े को दूसरे के ऊपर रखकर हमें ज्ञात होता है कि टुकड़े A और B का क्षेत्रफल एक समान है, टुकड़े C और E का क्षेत्रफल एक समान है। आप इन टुकड़ों से देख सकते हैं कि C और E टुकड़े, D को पूरा ढक लेते हैं। इसका अर्थ है कि D का क्षेत्रफल C और E से दुगुना है।]
उत्तर: A का क्षेत्रफल G के क्षेत्रफल का दुगुना है।
6. क्या अब आप सातों टुकड़ों से बने बड़े वर्ग के क्षेत्रफल को आकार C के क्षेत्रफल के रूप में लिख सकते हैं?
उत्तर: हां, सातों टुकड़ों से बने बड़े वर्ग का कुल क्षेत्रफल, आकार C के क्षेत्रफल के रूप में इस प्रकार लिखा जा सकता है:
कुल क्षेत्रफल = A + B + C + D + E + F + G = 4C+4C+1C+2C+1C+2C+2C = 16C
7. इन सातों टुकड़ों को व्यवस्थित करके एक आयत बनाइए। अब इस आयत का क्षेत्रफल, आकार ‘C’ के क्षेत्रफल के रूप में लिखने पर क्या प्राप्त होता है? अपने उत्तर का कारण बताइए।
उत्तर: जब सातों टुकड़ों को मिलाकर एक आयत बनाते हैं, तो उसका क्षेत्रफल भी वही रहता है — 16C
8. क्या इन सातों टुकड़ों से बने वर्ग और आयत के परिमाप भिन्न हैं या समान हैं? अपने उत्तर की व्याख्या कीजिए।
उत्तर: सातों टुकड़ों से बने वर्ग और आयत का परिमाप अलग-अलग होता है, क्योंकि इन दोनों आकृतियों की भुजाओं की लंबाई अलग होती है।
हालाँकि दोनों आकृतियाँ समान टुकड़ों से बनी हैं और उनका क्षेत्रफल एक जैसा होता है, लेकिन टुकड़ों की जमावट बदलने से आकृति की बाहरी सीमा (perimeter) भी बदल जाती है।
आइए पता लगाएँ (Page – 144)
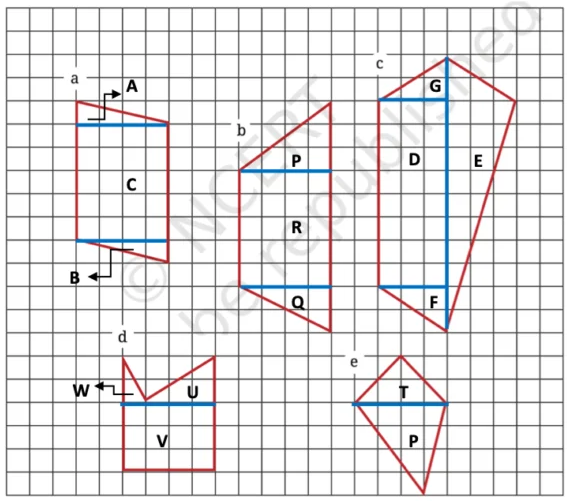
1. नीचे दी गई आकृतियों को आयत और त्रिभुजों में विभाजित करके क्षेत्रफल ज्ञात कीजिए:
उत्तर:
a. आकृति का क्षेत्रफल: = त्रिभुज A का क्षेत्रफल + त्रिभुज B का क्षेत्रफल + आयत C का क्षेत्रफल =
3 वर्ग इकाई + 3 वर्ग इकाई + 20 वर्ग इकाई = 26 वर्ग इकाई
b. आकृति का क्षेत्रफल: = त्रिभुज P का क्षेत्रफल + त्रिभुज Q का क्षेत्रफल + आयत R का क्षेत्रफल
= 6 वर्ग इकाई + 4 वर्ग इकाई + 20 वर्ग इकाई = 30 वर्ग इकाई
c. आकृति का क्षेत्रफल: = त्रिभुज G का क्षेत्रफल + त्रिभुज E का क्षेत्रफल + आयत F का क्षेत्रफल + आयत D का क्षेत्रफल
= 3 + 18 + 3 + 24 = 48 वर्ग इकाई
d. आकृति का क्षेत्रफल: = त्रिभुज W का क्षेत्रफल + त्रिभुज U का क्षेत्रफल + आयत V का क्षेत्रफल
= 1 + 3 + 12 = 16 वर्ग इकाई
e. आकृति का क्षेत्रफल = त्रिभुज T का क्षेत्रफल + त्रिभुज P का क्षेत्रफल
= 4 + 7 = 11 वर्ग इकाई
आइए पता लगाएँ (Page – 149)
1. एक आयत की विमाएँ बताइए जिसका क्षेत्रफल उन दो आयतों के क्षेत्रफल के योग के बराबर होगा, जिनकी विमाएँ 5 मी × 10 मी और 2 मी × 7 मी हैं।
उत्तर: दोनों आयतों का क्षेत्रफल इस प्रकार है:
पहले आयत का क्षेत्रफल = 5 मी × 10 मी = 50 वर्ग मी
दूसरे आयत का क्षेत्रफल = 2 मी × 7 मी = 14 वर्ग मी
इस प्रकार,
कुल क्षेत्रफल = 50 वर्ग मी + 14 वर्ग मी = 64 वर्ग मी
अब, यदि हमें 64 वर्ग मी क्षेत्रफल वाला एक आयत बनाना हो, तो उसकी लंबाई और चौड़ाई ऐसी होनी चाहिए कि उनका गुणनफल 64 हो।
पूर्णांकीय मापों में कुछ संभावित आयत की विमाएँ इस प्रकार हो सकती हैं:
- 64 मी × 1 मी
- 32 मी × 2 मी
- 16 मी × 4 मी
- 8 मी × 8 मी
इन सभी संयोजनों में क्षेत्रफल 64 वर्ग मीटर ही होगा।
2. 1000 वर्ग मी क्षेत्रफल वाले आयताकार पार्क की लंबाई 50 मी है, पार्क की चौड़ाई ज्ञात कीजिए।
उत्तर: आयताकार पार्क का क्षेत्रफल = 1000 वर्ग मीटर, लंबाई = 50 मीटर
क्षेत्रफल का सूत्र: क्षेत्रफल=लंबाई×चौड़ाई, 1000=50×चौड़ाई
चौड़ाई = \(\frac{1000}{50}\) = 20 मीटर
3. एक कमरे के फर्श की लंबाई 5 मी तथा चौड़ाई 4 मी है। 3 मी भुजा वाले एक वर्गाकार कालीन को फर्श पर बिछाया गया है। फर्श के उस भाग का क्षेत्रफल ज्ञात कीजिए जिस पर कालीन नहीं बिछा है।
उत्तर: फर्श का क्षेत्रफल = 5 × 4 वर्ग मी = 20 वर्ग मी
कालीन का क्षेत्रफल = 3 × 3 वर्ग मी = 9 वर्ग मी
अतः, फर्श के उस भाग का क्षेत्रफल, जिस पर कालीन नहीं बिछा है = (20 – 9) वर्ग मी = 11 वर्ग मी है।
4. 15 मी लंबे और 12 मी चौड़े एक पार्क के चारों कोनों को खोदकर फूलों की क्यारियाँ बनाई गई हैं, जिनकी लंबाई व चौड़ाई क्रमशः 2 मी और 1 मी है। एक लॉन बनाने के लिए अब कितना क्षेत्रफल उपलब्ध है?
उत्तर: पार्क की लंबाई 15 मीटर और चौड़ाई 12 मीटर है,
इसलिए उसका कुल क्षेत्रफल होगा: 15 × 12 वर्ग मी = 180 वर्ग मी
प्रत्येक फूलों की क्यारी का क्षेत्रफल: = 2 × 1 वर्ग मी = 2 वर्ग मी है।
चार क्यारियों का कुल क्षेत्रफल: = 4 × 2 = 8 वर्ग मी है।
अब, लॉन के लिए शेष उपलब्ध क्षेत्रफल: = (180 – 8) वर्ग मी = 172 वर्ग मी है।
5. आकृति A और आकृति B के परिमाप का क्षेत्रफल क्रमशः 18 वर्ग इकाई और 20 वर्ग इकाई है। आकृति A का परिमाप आकृति B के परिमाप से बड़ा है। दी गई स्थिति को पूरा करती हुई दो आकृतियाँ बनाएँ।
उत्तर:
क्षेत्रफल = 9 × 2 = 18 वर्ग इकाई
इसका परिमाप = 2(9 + 2) इकाई = 22 इकाई
क्षेत्रफल = 5 × 4 = 20 वर्ग इकाई
इसका परिमाप = 2(5 + 4) इकाई = 18 इकाई
यहाँ, आकार A का परिमाप B के परिमाप से अधिक है। (22 > 18)|
6. अपनी पुस्तक के एक पृष्ठ पर एक आयताकार हाशिया (border) बनाएँ जो ऊपर और नीचे से 1 सेमी की दूरी पर हो और बाईं व दाईं ओर से 1.5 सेमी दूरी पर हो। हाशिये का परिमाप क्या होगा?
उत्तर: हमें एक आयताकार हाशिया (border) बनाना है जो:
ऊपर और नीचे से = 1 सेमी खाली हो
बाएँ और दाएँ से = 1.5 सेमी खाली हो
अब मान लेते हैं कि पुस्तक के पृष्ठ का आकार है: 21 सेमी × 29.7 सेमी (आमतौर पर A4 साइज)
हाशिये की लंबाई और चौड़ाई निकालना
हाशिये की लंबाई (ऊपर-नीचे 1 सेमी हटाकर) = 29.7-1 – 1 = 27.7 सेमी
हाशिये की चौड़ाई (बाएँ-दाएँ 1.5 सेमी हटाकर) = 21−1.5−1.5 = 18 सेमी
परिमाप का सूत्र = परिमाप = 2×(लंबाई+चौड़ाई) = 2×(27.7+18) = 2×45.7 = 91.4सेमी
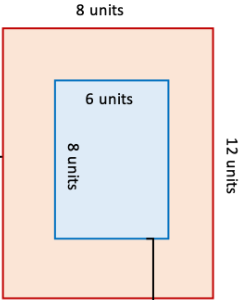
7. 12 इकाई × 8 इकाई आकार का एक आयत बनाइए। इसके अंदर एक अन्य आयत बनाइए जो बाह्य आयत को स्पर्श न करता हो और केवल आधा क्षेत्रफल घेरता हो।
उत्तर:
दिए गए आयत का क्षेत्रफल = 12 × 8 = 96 वर्ग इकाई
और नए आयत का क्षेत्रफल = 1 / 2 × 96 = 48 48 वर्ग इकाई
∴ नए आयत की संभावित भुजाएँ हो सकती हैं: 12 × 4, 16 × 3, 8 × 6, 1 × 48
∴ अतः, नए आयत की ऐसी माप (आठाई) जो 12 × 8 वाले आयत में समा सके = 8 इकाई × 6 इकाई








Leave a Reply