Question Answer For All Chapters – गणित प्रकाश Class 6th
भिन्न
आइए पता लगाएँ (Page 152-153)
रिक्त स्थानों में भिन्न संख्याओं को भरिए-
1. तीन अमरूदों का भार 1 किग्रा है। यदि वे लगभग समान आकार के हों, तो प्रत्येक अमरूद का लगभग भार ___________ किग्रा होगा।
उत्तर: \(\frac{1}{3}\)
2. एक थोक व्यापारी ने 1 किग्रा चावल को समान भार के चार पैकेटों में पैक किया। प्रत्येक पैकेट का भार ___________ किग्रा है।
उत्तर: \(\frac{1}{4}\)
3. चार मित्रों ने 3 गिलास गन्ने का रस का आर्डर दिया और इसे आपस में बराबर-बराबर बाँटा प्रत्येक ने ___________ गिलास गन्ने का रस पिया।
उत्तर: \(\frac{3}{4}\)
4. एक बड़ी मछली का भार \(\frac{1}{2}\) किग्रा है। एक छोटी मछली का भार \(\frac{1}{4}\) किग्रा है। दोनों का सम्मिलित भार है ____________ किग्रा।
उत्तर: \(\frac{1}{2}\) किग्रा + \(\frac{1}{4}\) किग्रा = \(\frac{3}{4}\) किग्रा
आइए पता लगाएँ (Page 155)
नीचे दिए गए चित्र एक संपूर्ण चिक्की की विभिन्न भिन्नात्मक इकाइयाँ दर्शाते हैं। प्रत्येक टुकड़ा पूरी चिक्की का कितना भाग है?
a. चित्र में संपूर्ण चिक्की को 2 बराबर भागों में बाँटा गया है और एक भाग दिखाया गया है। 1/2
b. चित्र में संपूर्ण चिक्की को 2 बराबर भागों में बाँटा गया है और पूरा एक भाग दिखाया गया है। 1/2
c. चित्र में चिक्की के 4 बराबर भागों में से 1 भाग दिखाया गया है। 1/4
d. चित्र में चिक्की को 4 बराबर भागों में बाँटा गया है और सभी 4 भाग दिखाई दे रहे हैं। 4/4 = 1 (पूर्ण चिक्की)
e. यह 3 टुकड़ों का बना है, प्रत्येक 1/4 के बराबर। 3/4
f. यह एक त्रिभुज है जो 2 भागों में बाँटी गई चिक्की का 1 भाग है। 1/2
g. यह एक छोटा वर्ग है जो चिक्की के 1/6 भाग के बराबर है। 1/6
h. यह एक त्रिभुज है जो चिक्की के 1/8 भाग जैसा लग रहा है। 1/8
आइए पता लगाएँ (Page 158)
1. 1/2 की इस तालिका को 2 और चरणों तक जारी रखें।
उत्तर:
2. क्या आप 1/4 के लिए समान तालिका बना सकते हैं?
उत्तर:
| चरण संख्या | जोड़ने की प्रक्रिया | योगफल (फल) | हिंदी में |
|---|---|---|---|
| 1 | 1/4 | 1/4 | 1 गुना चौथाई |
| 2 | 1/4 + 1/4 | 2/4 = 1/2 | 2 गुना चौथाई |
| 3 | 1/4 + 1/4 + 1/4 | 3/4 | 3 गुना चौथाई |
| 4 | 1/4 + 1/4 + 1/4 + 1/4 | 4/4 = 1 | 4 गुना चौथाई |
| 5 | 1/4 + 1/4 + 1/4 + 1/4 + 1/4 | 5/4 | 5 गुना चौथाई |
| 6 | 1/4 + 1/4 + 1/4 + 1/4 + 1/4 + 1/4 | 6/4 | 6 गुना चौथाई |
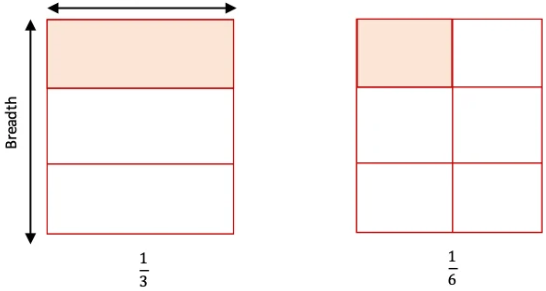
3. कागज की पट्टी की सहायता से 1/3 बनाएँ। क्या आप 1/6 बनाने में इसका उपयोग कर सकते हैं।
उत्तर:
4. एक चित्र बनाएँ और उपरोक्त के अनुसार योग कथन लिखिए-
(a) 1/4 रोटी का 5 गुना
(b) 1/4 रोटी का 9 गुना
उत्तर: (a) 1/4 रोटी का 5 गुना
(b) 1/4 रोटी का 9 गुना
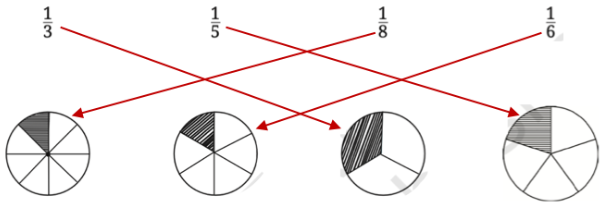
5. प्रत्येक भिन्नात्मक इकाई का सही चित्र के साथ जोड़ा बनाइए।
उत्तर:
आइए पता लगाएँ (Page 160)
1. संख्या रेखा पर 1/10, 3/4 और 4/5 लंबाइयों की रेखाओं को दर्शाइए।
उत्तर:
चरण 1: एक रेखा l खींचिए। उस पर एक बिंदु O चिह्नित कीजिए।
चरण 2: बिंदु O से 1 इकाई की दूरी पर एक बिंदु A चिह्नित कीजिए।
चरण 3: OA खंड को 10 समान भागों में विभाजित कीजिए।
अब,
- OP दर्शाता है: 1/10
- OQ दर्शाता है: 3/10
- OR दर्शाता है: 8/10 = 4/5
2. अपनी पसंद की पाँच और भिन्नों को लिखिए और उन्हें संख्या रेखा पर दर्शाइए।
उत्तर:
3. 0 और 1 के मध्य कितनी भिन्न होती हैं? सोचिए, अपने सहपाठियों से चर्चा कीजिए और अपना उत्तर लिखिए।
उत्तर: 0 और 1 के बीच अनगिनत भिन्न (fractions) होते हैं।
उदाहरण: 3/5, 4/5, 7/10, 1/2 आदि।
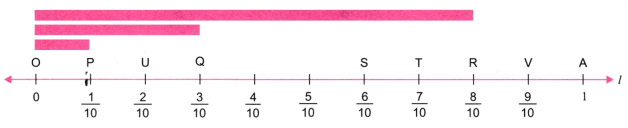
4. नीचे दर्शाई गई नीली रेखा और काली रेखा की लंबाइयाँ क्या हैं? 0 और 1 के मध्य की दूरी 1 इकाई लंबी है और यह दो बराबर भागों में विभाजित की गई है। अतः प्रत्येक भाग की लंबाई 1/2 है। इसलिए नीली रेखा 1/2 इकाई लंबी है। काली रेखा की लंबाई बताने वाली भिन्न को बॉक्स में लिखिए।
उत्तर:
5. काली रेखाओं की लंबाई बताने वाली भिन्नों को संबंधित बॉक्स में लिखिए।
उत्तर:
आइए पता लगाएँ (Page 162)
1. \(\frac{7}{2}\) में कितनी पूर्ण इकाइयाँ हैं?
उत्तर: \(\frac{7}{2}\) = 3\(\frac{7}{2}\)
इसका मतलब है:
- इसमें 3 पूर्ण इकाइयाँ हैं
- और एक अतिरिक्त आधा (1/2) भाग है
2. \(\frac{4}{3}\) और \(\frac{7}{3}\)में कितनी पूर्ण इकाइयाँ हैं?
उत्तर: \(\frac{4}{3}\) = 1\(\frac{1}{3}\)
- इसमें 1 पूर्ण इकाई है और 1/3 हिस्सा अतिरिक्त है।
\(\frac{7}{3}\) = 2\(\frac{1}{3}\)
- इसमें 2 पूर्ण इकाइयाँ हैं और 1/3 हिस्सा अतिरिक्त है।
आइए पता लगाएँ (Page 162)
उत्तर:


पूर्ण इकाइयाँ = 2, 2, 2
2. क्या 1 से बड़ी सभी भिन्नों को इस प्रकार से मिश्रित संख्या के रूप में लिख सकते हैं?
उत्तर: हाँ
3. निम्नलिखित भिन्नों को मिश्रित भिन्न के रूप में लिखिए (उदाहरणार्थ, \(\frac{9}{4}\) = 4\(\frac{1}{2}\)
उत्तर:
आइए पता लगाएँ (Page 163)
1. निम्नलिखित मिश्रित संख्याओं को भिन्न के रूप में लिखिए:
उत्तर:
आइए पता लगाएँ (Page 165)
1. क्या \(\frac{3}{6}\), \(\frac{4}{8}\), \(\frac{5}{10}\) तुल्य भिन्न हैं? क्यों?
उत्तर: हम जानते हैं कि दो या अधिक भिन्न तुल्य भिन्न (Equivalent Fractions) होते हैं यदि वे समान मान दर्शाते हैं।
चलिए, सभी भिन्नों को उनकी सरलतम रूप (lowest form) में बदलते हैं:
2. \(\frac{2}{6}\) के लिए वो तुल्य भिन्न लिखिए।
उत्तर: \(\frac{6}{18}\), \(\frac{8}{24}\)
3. \(\frac{4}{6}\) = ___________ = ________ = ___________ = __________ (जितनी संभव हों उतनी लिखिए।)
उत्तर:
आइए पता लगाएँ (Page 166)
1. तीन रोटियों को चार बच्चों में बराबर बाँटा गया है। चित्र में विभाजन दिखाएँ और प्रत्येक बच्चे को कितना भाग मिला है, भिन्न में लिखिए। संगत विभाजन क्रिया, योग क्रिया और गुणन क्रिया भी लिखिए।
प्रत्येक बच्चे को रोटी का मिला भाग- _____________
विभाजन क्रिया- _____________
योग क्रिया- _____________
गुणन क्रिया- _____________
अपने चित्र और उत्तरों की तुलना अपने सहपाठियों से कीजिए।
उत्तर: \(\frac{3}{4}\)
विभाजन क्रिया:
योग क्रिया: चारों बच्चों को मिला भाग जोड़ें:
गुणन क्रिया:
2. एक चित्र बनाकर दर्शाइए कि जब 2 रोटियाँ 4 बच्चों में बराबर-बराबर बाँटी जाती हैं, तो प्रत्येक बच्चे को कितना भाग मिलता है। इसके संगत भाग क्रिया, योग क्रिया और गुणन क्रिया भी लिखिए।
उत्तर:
3. अनिल एक समूह में था, जहाँ 2 केकों को 5 बच्चों में बराबर बाँटा गया। अनिल को कितना केक मिला होगा?
उत्तर: कुल केक = 2, कुल बच्चे = 5, सभी बच्चों को बराबर-बराबर केक बाँटे गए।
तो, प्रत्येक बच्चे को मिलेगा:
आइए पता लगाएँ (Page 168)
लुप्त संख्याएँ ज्ञात कीजिए-
(a) 4 मित्रों के बीच बराबर-बराबर बाँटा गया 5 गिलास जूस, 8 दोस्तों के बीच बराबर-बराबर बाँटे गए ____________ गिलास जूस के समान है।
उत्तर: यहाँ, जब 5 गिलास जूस को 4 मित्रों में बराबर-बराबर बाँटा जाता है,
तो प्रत्येक मित्र को मिलने वाला जूस होगा: =
अब, यदि हम चाहते हैं कि 8 मित्रों को भी उतना ही जूस मिले (जितना हर एक को ऊपर मिला),
तो हमें चाहिए:
(b) 4 किग्रा आलू को बराबर-बराबर 3 थैलों में भरा गया। ऐसे ही 12 किग्रा आलू को समान रूप से भरने के लिए ____________ थैलों की आवश्यकता होगी?
उत्तर:
(c) 5 बच्चों के बीच बराबर बाँटी गई 7 रोटियाँ और ____________ बच्चों के बीच बराबर बाँटी गई ____________ रोटियाँ समान होंगी।
उत्तर:
Page – 172
1. दिए गए भिन्न युग्मों के लिए तुल्य भिन्नों को ज्ञात कीजिए, जिसमें भिन्नात्मक इकाइयाँ समान हों।
उत्तर:
(a) \(\frac{7}{2}\) और \(\frac{3}{5}\)
हर (denominator) = 2 और 5 → LCM = 10
(b) \(\frac{8}{3}\) और \(\frac{5}{6}\)
3 और 6 का LCM = 6
(c) \(\frac{3}{4}\) और \(\frac{3}{5}\)
4 और 5 का LCM = 20
(d) \(\frac{6}{7}\) और \(\frac{8}{5}\)
7 और 5 का LCM = 35
(e) \(\frac{9}{4}\) और \(\frac{5}{2}\)
4 और 2 का LCM = 4
(f) \(\frac{1}{10}\) और \(\frac{2}{9}\)
10 और 9 का LCM = 90
(g) \(\frac{8}{3}\) और \(\frac{11}{4}\)
3 और 4 का LCM = 12
(h) \(\frac{13}{6}\) और \(\frac{1}{9}\)
6 और 9 का LCM = 18
आइए पता लगाएँ (Page 173)
1. निम्नलिखित भिन्नों को न्यूनतम पदों में व्यक्त कीजिए।
उत्तर:
(a) 17/51
17 एक अभाज्य संख्या (prime) है।
51 = 17 × 3
(b) 64/144
64 और 144 दोनों 16 से विभाज्य हैं:
(c) 126/147
126 और 147 दोनों 21 से विभाज्य हैं:
(d) 525/112
525 और 112 का कोई सामान्य भाजक नहीं है (सिर्फ 1)
(क्योंकि 525 = 3 × 5² × 7, और 112 = 2⁴ × 7)
केवल 7 दोनों में आता है, लेकिन:
आइए पता लगाएँ (Page 174)
1. निम्नलिखित भिन्नों की तुलना कीजिए और अपने उत्तर का कारण बताइए।
(a) \(\frac{8}{3}\) , \(\frac{5}{2}\)
(b) \(\frac{4}{9}\) , \(\frac{3}{7}\)
(c) \(\frac{7}{10}\) , \(\frac{9}{14}\)
(d) \(\frac{12}{5}\) , \(\frac{8}{5}\)
(e) \(\frac{9}{4}\) , \(\frac{5}{2}\)
2. निम्नलिखित भिन्नों को आरोही क्रम में लिखिए।
उत्तर: (a) \(\frac{7}{10}\) , \(\frac{11}{15}\), \(\frac{2}{5}\)
LCM निकालना
हर (denominator) हैं: 10, 15, और 5
इनका LCM = 30
अब हम सभी भिन्नों को ऐसा बनाएँगे कि उनका हर = 30 हो
सभी भिन्नों को हर 30 में बदलना
अब हमारे पास हैं: \(\frac{12}{30}\) , \(\frac{21}{30}\), \(\frac{22}{30}\)
आरोही क्रम: \(\frac{2}{5}\) , \(\frac{7}{10}\), \(\frac{11}{15}\)
(b) \(\frac{19}{24}\) , \(\frac{5}{6}\), \(\frac{7}{12}\)
हर (denominator) हैं: 24, 6, और 12
इनका LCM = 24
अब सभी भिन्नों को हर = 24 में बदलते हैं।
हर भिन्न को तुल्य भिन्न में बदलें
1. \(\frac{19}{24}\)
हर पहले से ही 24 है, कोई परिवर्तन नहीं = \(\frac{19}{24}\)
अब तुलना करें \(\frac{14}{24}\) , \(\frac{19}{24}\), \(\frac{20}{24}\)
आरोही क्रम (Ascending Order): \(\frac{7}{12}\) , \(\frac{19}{24}\), \(\frac{5}{6}\)
3. निम्नलिखित भिन्नों को अवरोही क्रम में लिखिए।
a. हर (denominator) हैं: 16, 8, 4 और 32 इनका LCM = 32
अब सभी भिन्नों को हर = 32 में बदलते हैं।
अब हम सभी भिन्नों को ऐसा बनाएँगे कि उनका हर = 32 हो
सभी भिन्नों को हर 32 में बदलना
\(\frac{25}{16}\) = \(\frac{25\times 2}{16\times 2}\) = \(\frac{50}{32}\)
\(\frac{7}{8}\) = \(\frac{7\times 4}{8\times 4}\) = \(\frac{28}{32}\)
\(\frac{13}{4}\) = \(\frac{13\times 8}{4\times 8}\) = \(\frac{104}{32}\)
\(\frac{17}{32}\) = \(\frac{17\times 1}{32\times 1}\) = \(\frac{17}{32}\)
b. हर (denominator) हैं: 4, 5, 12 और 4 इनका LCM = 60
अब सभी भिन्नों को हर = 60 में बदलते हैं।
अब हम सभी भिन्नों को ऐसा बनाएँगे कि उनका हर = 60 हो
सभी भिन्नों को हर 60 में बदलना
\(\frac{3}{4}\) = \(\frac{3\times 15}{4\times 15}\) = \(\frac{45}{60}\)
\(\frac{12}{5}\) = \(\frac{12\times 12}{5\times 12}\) = \(\frac{144}{60}\)
\(\frac{7}{12}\) = \(\frac{7\times 5}{12\times 5}\) = \(\frac{35}{60}\)
\(\frac{5}{4}\) = \(\frac{5\times 15}{4\times 15}\) = \(\frac{75}{60}\)
आइए पता लगाएँ (Page 179)
1. ब्रह्मगुप्त विधि का प्रयोग कर निम्नलिखित भिन्नों का योग ज्ञात कीजिए।
a. 1\(\frac{6}{7}\)
b. 1\(\frac{1}{12}\)
c. 1\(\frac{1}{2}\)
e. 1\(\frac{17}{60}\)
f. 1\(\frac{7}{15}\)
g. 1\(\frac{7}{15}\)
h. 1\(\frac{9}{40}\)
i. 5\(\frac{3}{4}\)
j. 2\(\frac{20}{21}\)
k. 1\(\frac{17}{60}\)
l. 1\(\frac{94}{105}\)
m. 6\(\frac{11}{12}\)
2. रहीम ने हरा पेंट बनाने के लिए \(\frac{2}{3}\) लीटर पीले पेंट को \(\frac{3}{4}\) लीटर नीले पेंट के साथ मिलाया। उसने कुल कितने लीटर हरा पेंट बनाया?
उत्तर:
3. एक मीटर परिधि के मेजपोश का संपूर्ण बॉर्डर (किनारा) बनाने के लिए गीता ने \(\frac{2}{5}\) मीटर लेस खरीदी और शमीम ने \(\frac{3}{4}\) मीटर लेस खरीदी। उन दोनों के द्वारा खरीदी गई लेस की कुल लंबाई ज्ञात कीजिए। क्या खरीदी गई लेस संपूर्ण बॉर्डर (किनारे) को ढकने के लिए पर्याप्त है?
उत्तर: खरीदे गए लेस की कुल लंबाई =
\(\frac{23}{4}\) मीटर
1\(\frac{3}{20}\) मीटर
हाँ, संपूर्ण बॉर्डर को ढकने के लिए यह लेस पर्याप्त होगी, क्योंकि 1\(\frac{3}{20}\) मीटर > 1 मीटर है।
आइए पता लगाएँ (Page 181)
उत्तर:
आइए पता लगाएँ (Page 182)
1. ब्रह्मगुप्त विधि का प्रयोग कर निम्नलिखित को घटाइए।
उत्तर:
2. संकेतानुसार घटाइए:
उत्तर:
3. निम्नलिखित प्रश्नों को हल कीजिए:
(a) जया का विद्यालय उसके घर से \(\frac{7}{10}\) किमी दूर है। वह प्रतिदिन विद्यालय पहुँचने के लिए \(\frac{1}{2}\) किमी ऑटो से जाती है और शेष दूरी पैदल चलकर तय करती है। वह स्कूल पहुँचने के लिए प्रतिदिन कितना पैदल चलती है?
उत्तर:
(b) जीविका पार्क का एक पूरा चक्कर लगाने में \(\frac{10}{3}\) मिनट लेती है और उसकी मित्र नमिता उसी कार्य को करने में \(\frac{13}{4}\) मिनट का समय लेती है। दोनों में से कौन कम समय में पूरा चक्कर लगाती है और कितना कम समय लेती है?
उत्तर:






















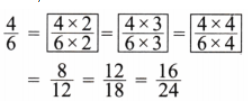



































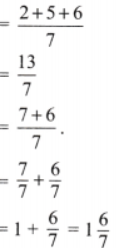



















Leave a Reply