गणित प्रकाश Question Answer Chapter 8 Class 6 Ganit Prakash Maths Hindi Medium

Question Answer For All Chapters – गणित प्रकाश Class 6th

रचनाओं के साथ खेलना

आइए पता लगाएँ (Page 191)

1. यह अर्ध-वृत बनाने के लिए परकार में कितनी लंबाई की त्रिज्या रखनी होगी? AX की लंबाई क्या होनी चाहिए?

उत्तर: हमारे पास AB = 8 सेमी है।
चूँकि “Wavy Wave” में दो समान अर्धवृत्त हैं, इसलिए AX = XB होगा।
∴ X, रेखा AB का मध्य बिंदु है।

∴ AX = \(\frac{2}{3}\) = 4 सेमी

∴ AX की लंबाई 4 सेमी है।

मान लें कि M, AX का मध्य बिंदु है।
∴ AM = MX = \(\frac{2}{3}\) = 2 सेमी

M ही अर्धवृत्त का केंद्र है।
∴ अर्धवृत्त की त्रिज्या = AM = 2 सेमी

2. भिन्न लंबाई का एक केंद्रीय रेखा (खंड) लीजिए तथा इस पर लहर बनाने का प्रयास कीजिए।

उत्तर:

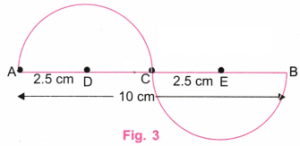
चरण 1: हम विभिन्न लंबाई की एक केंद्रीय रेखा से शुरुआत करते हैं, उदाहरण के लिए — 10 सेमी की रेखा।

चरण 2: चूँकि \(\frac{10}{2}\) = 5

इसलिए स्केल (रूलर) की सहायता से AB पर एक बिंदु C चिह्नित करें, ताकि AC = 5 सेमी हो।
इस प्रकार, C बिंदु AB का मध्य बिंदु है।

अब, \(\frac{5}{2}\) = 2.5

इसलिए स्केल की सहायता से AC पर एक बिंदु D लें और CB पर एक बिंदु E लें, ताकि:

• AD = 2.5 सेमी
• CE = 2.5 सेमी

इस प्रकार:

• D बिंदु, AC का मध्य बिंदु है, और
• E बिंदु, CB का मध्य बिंदु है।

चरण 3: D को केंद्र मानकर, 2.5 सेमी त्रिज्या में परकार की सहायता से केंद्रीय रेखा AB के ऊपर एक अर्धवृत्त बनाइए।
फिर, E को केंद्र मानकर, 2.5 सेमी त्रिज्या में परकार की सहायता से केंद्रीय रेखा AB के नीचे एक अर्धवृत्त बनाइए।

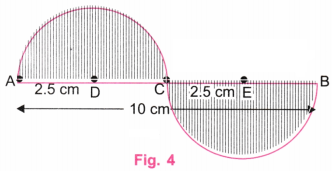
चरण 4: रेखा AB के ऊपर और नीचे बने अर्धवृत्तों के भीतर लंबवत रेखाएँ (ऊर्ध्वाधर रेखाएँ) खींचिए।

चरण 5: यह आकृति “Wavy Wave” (लहरदार तरंग) का आवश्यक चित्रण दर्शाती है, जिसमें केंद्रीय रेखा की लंबाई 10 सेमी है।

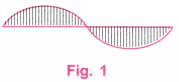
3. उन आकृतियों को पुनः बनाएँ जहाँ लहरें अर्ध-वृत से छोटी हैं (जैसा कि पिछले पृष्ठ पर दी ‘एक व्यक्ति’ के गले की आकृति में दिखाई देता है।) यहाँ चुनौती यह है कि दोनों लहरें समान हों। यह कठिन हो सकता है।

उत्तर: हम एक “लहरदार तरंग” (Wavy Wave) बनाएँगे।

यहाँ, तरंगें (waves) अर्धवृत्त से छोटी हैं।

चरण 1: हम 10 सेमी लंबाई की एक केंद्रीय रेखा AB से शुरुआत करते हैं।

चरण 2:
चूँकि 10÷2 = 5, इसलिए स्केल (रूलर) की सहायता से AB पर एक बिंदु C चिह्नित करें, ताकि AC = 5 सेमी हो।
इस प्रकार, C बिंदु AB का मध्य बिंदु है।

अब, 5÷2 = 2.5
इसलिए स्केल की सहायता से AC पर एक बिंदु D और CB पर एक बिंदु E चिह्नित करें, ताकि:

• AD = 2.5 सेमी
• CE = 2.5 सेमी

इस प्रकार:

• D, AC का मध्य बिंदु है
• E, CB का मध्य बिंदु है।

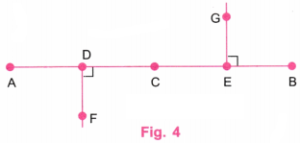
चरण 3: D बिंदु पर, प्रोट्रैक्टर (कोण मापक) की सहायता से AB के नीचे की ओर एक लंबवत रेखा खींचिए।
इसी प्रकार, E बिंदु पर, प्रोट्रैक्टर की सहायता से AB के ऊपर की ओर एक लंबवत रेखा खींचिए।

चरण 4: स्केल (रूलर) की सहायता से बिंदु F और G इस प्रकार चिह्नित करें कि:

• DF = 1.5 सेमी
• EG = 1.5 सेमी

यह दूरी (DF और EG) समान होनी चाहिए, और यह 1.5 सेमी से थोड़ी कम या ज्यादा भी हो सकती है।

चरण 5:
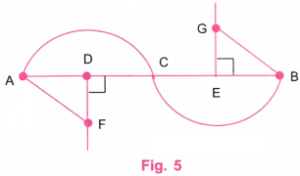
AF और BG रेखा खंडों को आपस में मिलाइए।

अब:

• केंद्र F पर रखते हुए, A से C तक एक चाप (arc) बनाइए जिसकी त्रिज्या AF के बराबर हो।
• केंद्र G पर रखते हुए, B से C तक एक चाप बनाइए जिसकी त्रिज्या GB के बराबर हो।

चरण 6: चित्र 5 में लंबवत (ऊर्ध्वाधर) रेखाएँ खींचिए।
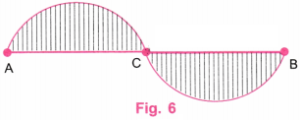
फिर, चित्र 6 के अनुसार, चित्र 5 में बनी अतिरिक्त रेखाओं को मिटा दीजिए।

चरण 7: चित्र 6 उस आवश्यक “लहरदार तरंग” (Wavy Wave) का चित्रण दर्शाता है, जिसमें तरंगें अर्धवृत्त से छोटी हैं।

Page 191

इनमें से कौन-सा नाम चित्र में दिखाए गए वर्ग के लिए मान्य नहीं है?

1. PQSR
2. SPQR
3. RSFQ
4. QRSP

उत्तर: 1.PQSR

आइए पता लगाएँ (Page 194)

1. डॉट पेपर पर एक आयत और चार वर्गों का प्रारूप खींचिए (जैसा आकृति 8.3 में दिखाया गया है) आकृति को पुनः इस प्रकार बनाने के लिए कि चारों वर्ग सममित रूप से आयत के चारों ओर रखे जाएँ, आप क्या करेंगे? अपने सहपाठियों के साथ चर्चा कीजिए।

उत्तर: चरण 1: एक वर्ग बिंदु ग्रिड वाला काग़ज़ (square dot paper) लें और उस पर एक बिंदु A पर चिह्नित करें।
अब A से शुरू करते हुए दाएँ की ओर 10 बिंदु गिनें और 10वें बिंदु को B के रूप में चिह्नित करें।

चरण 2: अब B से ऊपर की ओर 6 बिंदु गिनें और 6वें बिंदु को C के रूप में चिह्नित करें।
फिर A से ऊपर की ओर 6 बिंदु गिनें और 6वें बिंदु को D के रूप में चिह्नित करें।
अब AB, BC, CD और DA को रेखाओं द्वारा आपस में जोड़ें।

चरण 3: चित्र में दिए गए अनुसार, बिंदु E, F, G और H को डॉट पेपर पर चिह्नित करें।

चरण 4: अब E, F, G और H से 4 बिंदुओं की दूरी पर बिंदु I, J, K और L को क्रमशः चिह्नित करें।
फिर IE, FJ, GK और LH को रेखाओं से जोड़ें।

चरण 5: LH और GK रेखाओं पर, आयत के ऊपर की ओर वर्ग बनाएँ।

चरण 6: IE और FJ रेखाओं पर, आयत के नीचे की ओर वर्ग बनाएँ।

चरण 7: यह आकृति एक आयत और चार वर्गों की आवश्यक संरचना (configuration) को दर्शाती है, जो वर्ग बिंदु ग्रिड वाले काग़ज़ (square dot paper) पर बनी है।

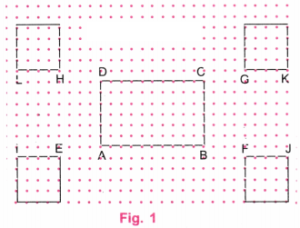
2. पहचानिए कि क्या इस संग्रह में कोई वर्ग है। यदि आवश्यकता हो तो मापन का प्रयोग कीजिए।

सोचिए- उपरोक्त आकृति में बिना मापन उपकरणों को प्रयोग किए, क्या यह बताना संभव है कि भुजाएँ बराबर हैं या नहीं, कोण समकोण हैं या नहीं? क्या हम यह केवल डॉट पेपर में शीर्षों की स्थिति देखकर ज्ञात कर सकते हैं?

उत्तर:

चित्र I:
इस चित्र में, AB और BC समान नहीं हैं।
इसलिए, ABCD एक वर्ग नहीं हो सकता।

चित्र II:
इस चित्र में, ∠BAD = 90° नहीं है।
इसलिए, ABCD एक वर्ग नहीं हो सकता।

चित्र III:
इस चित्र में, बिंदुओं की गिनती करने पर पता चलता है कि AB, BC, CD और DA सभी भुजाएँ समान हैं।
साथ ही, बिंदुओं की स्थिति यह दर्शाती है कि ABCD के प्रत्येक कोण 90° के हैं।
∴ ABCD एक वर्ग है।

चित्र IV:
इस चित्र में, बिंदुओं की गिनती करने पर पाया जाता है कि AB, BC, CD और DA सभी भुजाएँ समान हैं।
साथ ही, कोण मापक (protractor) की सहायता से यह ज्ञात होता है कि ABCD के सभी कोण 90° हैं।
∴ ABCD एक वर्ग है।

3. डॉट पेपर पर एक कम-से-कम 3 घुमाए गए वर्ग और 3 घुमाए गए आयत खींचिए। उन्हें इस प्रकार खींचिए कि उनके कोने डॉट पेपर के डॉट्स (बिंदु) पर हों। जाँच कीजिए कि आपने जो वर्ग और आयत बनाए हैं, वे उनके संगत गुणों को संतुष्ट करते हैं या नहीं।

उत्तर: हम एक डॉट ग्रिड (बिंदु ग्रिड) पर दो घुमाए गए वर्ग और दो घुमाए गए आयत बनाते हैं, इस प्रकार कि वर्गों और आयतों के कोने डॉट्स (बिंदुओं) पर हों।

हमने दो घुमाए गए वर्ग (II और III) तथा दो घुमाए गए आयत (I और IV) बनाए हैं।
इन वर्गों और आयतों को बनाते समय, हमने भुजाओं के बीच के डॉट्स (बिंदुओं) की संख्या और भुजाओं की स्थिति का ध्यान रखा है।

कोण मापक (प्रोट्रैक्टर) का उपयोग करके हमें पता चलता है कि आकृतियों I से IV तक के सभी कोण 90° हैं।
स्केल (रूलर) का उपयोग करके हमें यह ज्ञात होता है कि:
आकृतियाँ I और IV की विपरीत भुजाएँ समान हैं,
और आकृतियाँ II और III की सभी भुजाएँ समान हैं।
∴ परिभाषा के अनुसार:
आकृतियाँ I और IV आयत (Rectangles) हैं।
आकृतियाँ II और III वर्ग (Squares) हैं।

रचना कीजिए (Page 197)

1. 6 सेमी और 4 सेमी लंबी भुजाओं वाले एक आयत की रचना कीजिए ? रचना के बाद जाँच कीजिए कि क्या ये आयत के दोनों गुणों को संतुष्ट करता है?

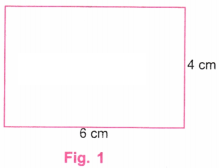
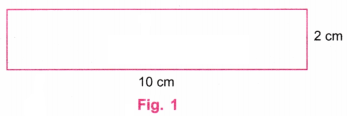
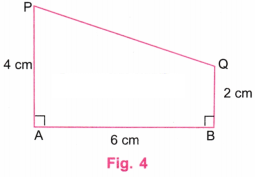
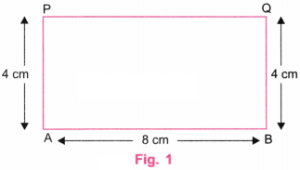
उत्तर: हम चित्र 1 में दिखाई गई आकृति के रूप में एक आयत बनाएँगे।

चरण 1: स्केल (रूलर) की सहायता से AB नाम की एक रेखा खींचिए जिसकी लंबाई 6 सेमी हो।

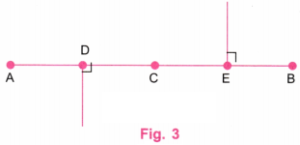
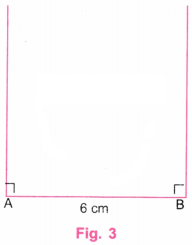
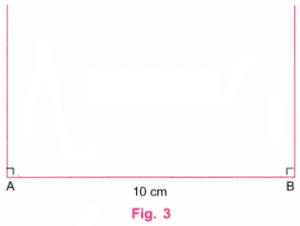
चरण 2: कोण मापक (प्रोट्रैक्टर) की सहायता से, बिंदु A और बिंदु B पर लंबवत रेखाएँ खींचिए। (चित्र 3 देखें)

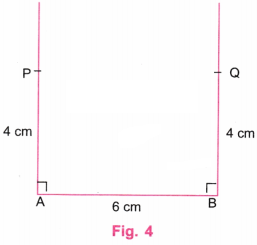
चरण 3: स्केल (रूलर) की सहायता से, बिंदु A पर खींची गई लंबवत रेखा पर एक बिंदु P ऐसा चिह्नित करें कि AP = 4 सेमी हो।
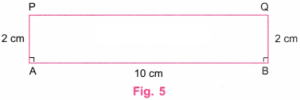
इसी प्रकार, बिंदु B पर खींची गई लंबवत रेखा पर एक बिंदु Q ऐसा चिह्नित करें कि BQ = 4 सेमी हो। (चित्र 4 देखें)

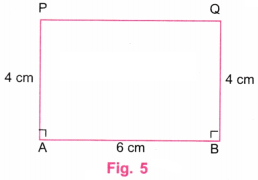
चरण 4: स्केल (रूलर) की सहायता से बिंदु P और Q को आपस में जोड़िए।
फिर, P और Q के ऊपर की अतिरिक्त रेखाओं को मिटा दीजिए। (चित्र 5 देखें)

चरण 5: स्केल (रूलर) की सहायता से जाँच कीजिए कि PQ की लंबाई 6 सेमी है।
कोण मापक (प्रोट्रैक्टर) की सहायता से जाँच कीजिए कि ∠P और ∠Q दोनों 90° हैं।

चरण 6: हमारे पास है:
(i) AB = PQ = 6 सेमी और AP = BQ = 4 सेमी
(ii) ∠A = ∠B = ∠P = ∠Q = 90°

चरण 7: चित्र 5 में ABQP वह आवश्यक आयत (Rectangle) है जिसकी भुजाएँ 4 सेमी और 6 सेमी हैं।

2. 2 सेमी और 10 सेमी भुजाओं वाले एक आयत की रचना कीजिए। रचना के बाद जाँच कीजिए कि क्या ये आयत के दोनों गुणों को संतुष्ट करता है?

उत्तर: हम चित्र 1 में दिखाई गई आकृति के रूप में एक आयत बनाएँगे।

चरण 1: स्केल (रूलर) की सहायता से AB नाम की एक रेखा खींचिए जिसकी लंबाई 10 सेमी हो। (चित्र 2 देखें)

चरण 2: कोण मापक (प्रोट्रैक्टर) की सहायता से, बिंदु A और बिंदु B पर लंबवत रेखाएँ खींचिए। (चित्र 3 देखें)

चरण 3: स्केल (रूलर) की सहायता से, बिंदु A पर खींची गई लंबवत रेखा पर एक बिंदु P ऐसा चिह्नित करें कि AP = 2 सेमी हो।
इसी प्रकार, बिंदु B पर खींची गई लंबवत रेखा पर एक बिंदु Q ऐसा चिह्नित करें कि BQ = 2 सेमी हो। (चित्र 4 देखें)

चरण 4: स्केल (रूलर) की सहायता से बिंदु P और Q को सीधी रेखा से जोड़िए।
फिर, P और Q के ऊपर की अतिरिक्त लंबवत रेखाओं को मिटा दीजिए। (चित्र 5 देखें)।

चरण 5: स्केल (रूलर) की सहायता से जाँच कीजिए कि PQ की लंबाई 10 सेमी है।
कोण मापक (प्रोट्रैक्टर) की सहायता से जाँच कीजिए कि ∠P और ∠Q दोनों 90° हैं।

चरण 6: हमारे पास है:
(i) AB = PQ = 10 सेमी और AP = BQ = 2 सेमी
(ii) ∠A = ∠B = ∠P = ∠Q = 90°

चरण 7: चित्र 5 में ABQP वह आवश्यक आयत (Rectangle) है जिसकी भुजाएँ 2 सेमी और 10 सेमी हैं।

3. क्या 4 भुजाओं वाली ऐसी आकृति की रचना करना संभव है, जिसमें-

• सभी कोण 90° के बराबर हों, परंतु
• सम्मुख भुजाएँ बराबर नहीं हों?

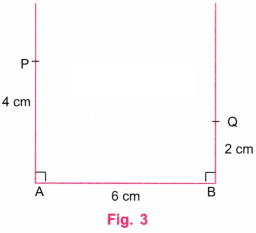
उत्तर: चरण 1: स्केल (रूलर) की सहायता से AB नाम की एक रेखा खींचिए जिसकी लंबाई 6 सेमी हो। (चित्र 1 देखें)

चरण 2: कोण मापक (प्रोट्रैक्टर) की सहायता से, बिंदु A और बिंदु B पर लंबवत रेखाएँ खींचिए। (चित्र 2 देखें)

चरण 3: स्केल (रूलर) की सहायता से, बिंदु A पर खींची गई लंबवत रेखा पर एक बिंदु P ऐसा चिह्नित करें कि AP = 4 सेमी हो।
इसी प्रकार, बिंदु B पर खींची गई लंबवत रेखा पर एक बिंदु Q ऐसा चिह्नित करें कि BQ = 2 सेमी हो, जो कि AP के बराबर नहीं है। (चित्र 3 देखें)

चरण 4: चित्र 3 में, रेखाएँ AP और BQ सम्मुख भुजाएँ हैं, लेकिन ये बराबर नहीं हैं।
अब स्केल (रूलर) की सहायता से बिंदु P और Q को आपस में जोड़िए।
फिर, P और Q के ऊपर की अतिरिक्त रेखाओं को मिटा दीजिए। (चित्र 4 देखें)

चरण 5: कोण मापक (प्रोट्रैक्टर) की सहायता से मापने पर हमें पता चलता है कि न तो ∠P और न ही ∠Q 90° के हैं।

चरण 6: इससे हम यह निष्कर्ष निकालते हैं कि:
ऐसी किसी 4 भुजाओं वाली आकृति की रचना संभव नहीं है,
जिसमें सभी कोण 90° के हों, लेकिन विपरीत भुजाएँ बराबर न हों।

रचना कीजिए (Page 199)

आयतों को तोड़ना

1. एक ऐसे आयत की रचना कीजिए जिसे 3 समरूप वर्गों में विभाजित किया जा सके।

उत्तर: हम चित्र 1 में दिखाई गई आकृति के रूप में एक आयत बनाएँगे।

चरण 1: मान लीजिए कि आयत की ऊर्ध्वाधर भुजा (लंबाई) 3 सेमी है।
चूँकि इस आयत को तीन समान वर्गों में बाँटना है, इसलिए आयत की क्षैतिज भुजा (चौड़ाई) होगी:
3 सेमी + 3 सेमी + 3 सेमी = 9 सेमी।

चरण 2: स्केल (रूलर) की सहायता से AB नाम की एक रेखा खींचिए जिसकी लंबाई 9 सेमी हो। (चित्र 2 देखें)।

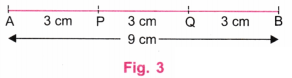
चरण 3: स्केल (रूलर) की सहायता से, AB रेखा पर दो बिंदु P और Q इस प्रकार चिह्नित करें कि:

• AP = 3 सेमी
• PQ = 3 सेमी

इस प्रकार, शेष भाग QB = 3 सेमी होगा। (चित्र 3 देखें)

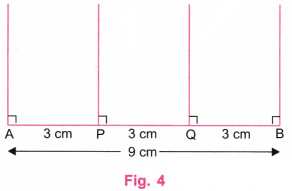
चरण 4: कोण मापक (प्रोट्रैक्टर) की सहायता से, बिंदुओं A, P, Q और B पर लंबवत रेखाएँ खींचिए। (चित्र 4 देखें)

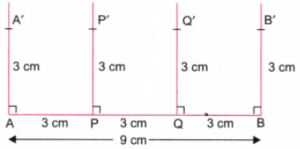
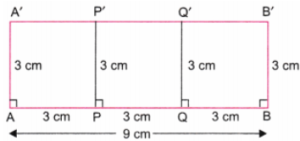
चरण 5: स्केल (रूलर) की सहायता से, बिंदुओं A, P, Q और B पर खींची गई लंबवत रेखाओं पर क्रमशः बिंदु A’, P’, Q’ और B’ इस प्रकार चिह्नित करें कि:

AA’ = PP’ = QQ’ = BB’ = 3 सेमी हों। (चित्र 5 देखें)

चरण 6:
स्केल (रूलर) की सहायता से निम्न रेखाएँ खींचिए:

• A’ और P’ को जोड़िए
• P’ और Q’ को जोड़िए
• Q’ और B’ को जोड़िए

फिर, A’, P’, Q’ और B’ के ऊपर की अतिरिक्त रेखाओं को मिटा दीजिए। (चित्र 6 देखें)

चरण 7: ABB’A’ वह आवश्यक आयत (rectangle) है जिसे तीन समान वर्गों में विभाजित किया गया है:

• APP’A’
• PQQ’P’
• QBB’Q’

ये तीनों वर्ग आकार और आकार में समान हैं।

Page 201

उस आयत की भुजाओं की लंबाई बताइए, जिसे निम्नलिखित में विभाजित नहीं किया जा सकता है-

• दो समरूप वर्ग
• तीन समरूप वर्ग

उत्तर: 1. दो समरूप वर्गों में विभाजित नहीं होने वाली आयत की भुजाएँ:
ऐसी आयत जिसमें

एक भुजा = 5 सेमी

दूसरी भुजा = 7 सेमी

तो यह दो समान वर्गों में विभाजित नहीं की जा सकती क्योंकि वर्गों के लिए आयत की एक भुजा दूसरी की गुणज (multiple) होनी चाहिए — जैसे 4 और 8, 3 और 6, आदि।

2. तीन समरूप वर्गों में विभाजित नहीं होने वाली आयत की भुजाएँ:
ऐसी आयत जिसमें

एक भुजा = 4 सेमी

दूसरी भुजा = 11 सेमी

तो यह आयत तीन समान वर्गों में नहीं बँट सकती, क्योंकि लंबी भुजा छोटी भुजा की तीन गुना नहीं है, और तीन बराबर वर्ग बनाने के लिए यही आवश्यक होता है।

रचना कीजिए (Page 201, 202, 203)

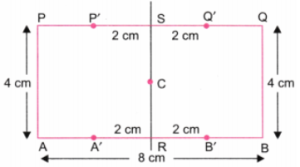
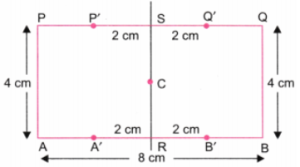
1. 8 सेमी और 4 सेमी भुजाओं वाले एक आयत की रचना कीजिए। इस आयत के अंदर आप नीचे आकृति में दर्शाए अनुसार एक वर्ग की रचना किस प्रकार करेंगे, जिससे कि यह वर्ग आयत के ठीक बीचों-बीच रहे?

[संकेत- एक कच्ची (रफ) आकृति खींचिए। इस वर्ग की भुजा क्या होगी ? बाहरी आयत और वर्ग के कोनों के बीच में कितनी दूरी होगी?]

उत्तर: किसी आयत (या वर्ग) का केंद्र वह बिंदु होता है जहाँ उसकी दोनों विकर्ण रेखाएँ एक-दूसरे को काटती हैं।

चरण 1: स्केल (रूलर) की सहायता से AB नाम की एक रेखा खींचिए जिसकी लंबाई 8 सेमी हो।
कोण मापक (प्रोट्रैक्टर) की सहायता से बिंदु A और B पर लंबवत रेखाएँ खींचिए।

अब, स्केल की सहायता से:

• A पर खींची गई लंबवत रेखा पर बिंदु P ऐसा चिह्नित करें कि AP = 4 सेमी हो।
• B पर खींची गई लंबवत रेखा पर बिंदु Q ऐसा चिह्नित करें कि BQ = 4 सेमी हो।

अब P और Q को सीधी रेखा से जोड़िए।
फिर, P और Q के ऊपर की अतिरिक्त रेखाओं को मिटा दीजिए। (चित्र 1 देखें)

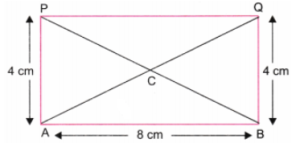
चरण 2: स्केल (रूलर) की सहायता से AQ और BP विकर्ण (diagonals) खींचिए।
मान लीजिए कि ये दोनों विकर्ण बिंदु C पर एक-दूसरे को काटते हैं।

यह बिंदु C, आयत ABQP का केंद्र है और साथ ही आवश्यक वर्ग (required square) का भी केंद्र है। (चित्र 2 देखें)

चरण 3: विकर्ण AQ और BP को मिटा दीजिए।
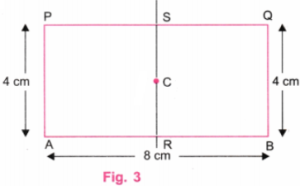
अब कोण मापक (प्रोट्रैक्टर) की सहायता से AB रेखा पर बिंदु C से होकर गुजरती हुई एक लंबवत रेखा खींचिए।
यह लंबवत रेखा AB को बिंदु R पर तथा PQ को बिंदु S पर काटेगी। (चित्र 3 देखें)

चरण 4: चूँकि AP = 4 सेमी, तो वर्ग की प्रत्येक भुजा 4 सेमी होगी।

• AB पर: A’R = 2 सेमी, RB’ = 2 सेमी ⇒ A’B’ = 4 सेमी
• PQ पर: P’S = 2 सेमी, SQ’ = 2 सेमी ⇒ P’Q’ = 4 सेमी (चित्र 4 देखें)

चरण 5: एक पैमाने की सहायता से, A’ और P’ को जोड़ें तथा B’ और Q’ को भी जोड़ें। फिर रेखा RS को मिटा दें। (चित्र 5)।

चरण 6. चित्र 5 में, A’B’Q’P’ वह आवश्यक वर्ग है जिसका केन्द्र C है, जो दिए गए आयत का भी केन्द्र है।

2. सुनिश्चित करें कि वर्ग उसी तरह संरेखित हों जिस तरह वे दिखाए गए हैं।

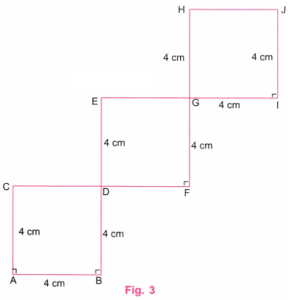
गिरते हुए वर्ग

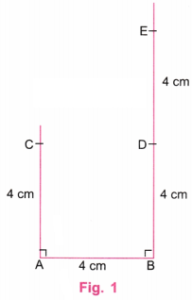
उत्तर: दिए गए चित्र में तीन गिरते हुए वर्ग हैं और प्रत्येक वर्ग की भुजा 4 सेमी है।

चरण 1: स्केल का उपयोग करके AB रेखा खींचिए जिसकी लंबाई 4 सेमी हो। प्रोटेक्टर (कोणमापक यंत्र) की सहायता से बिंदु A और B पर लंब रेखाएँ खींचिए।
स्केल की सहायता से बिंदु A पर खींची गई लंब रेखा पर बिंदु C इस प्रकार चिन्हित कीजिए कि AC = 4 सेमी हो।
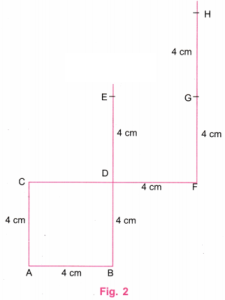
फिर स्केल की सहायता से बिंदु B पर खींची गई लंब रेखा पर बिंदु D और E इस प्रकार चिन्हित कीजिए कि BD = 4 सेमी और DE = 4 सेमी हो। (चित्र 1)।

चरण 2: बिंदु C और D को जोड़िए। रेखा CD को आगे बढ़ाते हुए इस प्रकार बढ़ाइए कि DF = 4 सेमी हो और नया बिंदु F प्राप्त हो।
प्रोटेक्टर (कोणमापक यंत्र) की सहायता से बिंदु F पर एक लंब रेखा खींचिए।
फिर स्केल का उपयोग करके उस लंब रेखा पर बिंदु G और H इस प्रकार चिन्हित कीजिए कि FG = 4 सेमी और GH = 4 सेमी हो। (चित्र 2)।

चरण 3: बिंदु E और G को जोड़िए। रेखा EG को आगे बढ़ाइए ताकि GE = 4 सेमी हो और नया बिंदु I प्राप्त हो।
प्रोटेक्टर (कोणमापक यंत्र) की सहायता से बिंदु I पर एक लंब रेखा खींचिए।
फिर स्केल की सहायता से उस लंब रेखा पर बिंदु J इस प्रकार चिन्हित कीजिए कि IJ = 4 सेमी हो।
अब बिंदु H और J को जोड़िए।
चित्र में बनी अतिरिक्त रेखाओं को मिटा दीजिए। (चित्र 3)।

चरण 4: चित्र 3 ही वांछित आकृति है जिसमें तीन “गिरते हुए वर्ग” हैं और प्रत्येक वर्ग की भुजा 4 सेमी है।

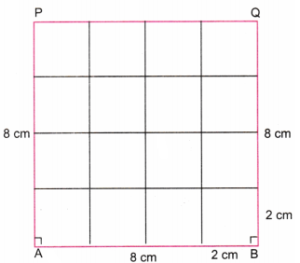
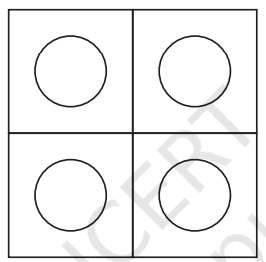
3. छायांकन

दी गई आकृति को बनाइए। अपनी इच्छा से मापन चुनिए। ध्यान दीजिए कि बड़ी चतुर्भुजीय आकृति एक वर्ग है तथा इसी प्रकार छोटी आकृतियाँ भी वर्ग हैं।

चरण 1. एक रूलर का उपयोग करके 8 सेमी की एक रेखा AB खींचे। क्योंकि 8 + 4 = 2 हम 2 सेमी भुजा के छोटे वर्ग खींचेंगे एक चाँदा का उपयोग करके A और B पर लंबवत् रेखाएँ खींचे। एक रूलर का उपयोग करके A पर लंबवत् रेखा पर बिंदु P को इस तरह चिह्नित करें कि AP = 8 सेमी। एक रूलर का उपयोग करके, B पर लंबवत् रेखा पर बिंदु Q को इस तरह चिह्नित करें कि BQ = 8 सेमी। एक रूलर का उपयोग करके P और Q को मिलाएँ। P और Q के ऊपर की रेखाओं को मिटा दें।

चरण 2. रेखाओं AB, BQ, QP और PA पर एक रूलर का उपयोग करके 2 सेमी की दूरी पर बिंदु चिह्नित करें। 16 वर्ग प्राप्त करने के लिए क्षैतिज और लंबवत रेखाएँ खींचें।

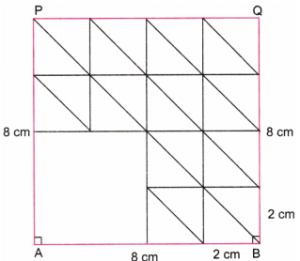
चरण 3. कोने A से, चार वर्गों की भीतरी भुजाओं को मिटाकर 4 सेमी भुजा वाला एक वर्ग प्राप्त करें, जिसमें कोना A पर हो। 2 सेमी भुंजा वाले शेष 12 छोटे वर्गों के समांतर विकर्ण खींचें।

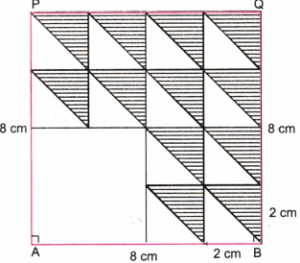
चरण 4. 12 छोटे वर्गों से, विकर्णों के ऊपर वाले भाग में क्षैतिज रेखाएँ खींचें।

चरण 5. आकृति 4 वह वांछित आकृति है, जिसमें एक वर्ग में 12 छोटे वर्ग है।

4. वर्ग जिसके अंदर छेद है

ध्यान दें कि वृत्ताकार छेद, वर्ग के ठीक बीचों बीच है।
[संकेत सोचिए कि वृत्त का केंद्र कहाँ होना चाहिए।]

उत्तर: एक वर्ग का केंद्र उसके विकर्णों का प्रतिच्छेद बिंदु होता है। यह केंद्र आकृति में छेद का केंद्र भी है।

चरण 1. रूलर से 5 सेमी की रेखा AB खींचें।
A और B पर चांदा (सेट स्क्वेयर) से लंब रेखाएँ बनाएं।
A की लंब रेखा पर बिंदु P इस तरह चिह्नित करें कि AP = 5 सेमी हो।
B की लंब रेखा पर बिंदु Q इस तरह चिह्नित करें कि BQ = 5 सेमी हो।
P और Q को रूलर से जोड़ें और उनके ऊपर की रेखाएँ मिटा दें।

चरण 2. रूलर से विकर्ण AQ और BP खींचें।
मान लीजिए ये विकर्ण बिंदु C पर कटते हैं — यही वर्ग ABQP का केंद्र है।
अब विकर्ण AQ और BP को मिटा दें।

चरण 3. C को केंद्र मानें और कंपास में 1.5 सेमी की त्रिज्या रखें।
अब कंपास से एक वृत्त खींचें।

चरण 4. आकृति 3 ‘वर्ग जिसके अंदर छेद है’ की अभीष्ट आकृति है।

5. अधिक छेदों वाले वर्ग

आकृति में, एक वृत्त का केंद्र संबंधित वर्ग के समान है।

चरण 1 : रूलर से 8 सेमी लंबी रेखा AB खींचें।
चाँदा (सेट स्क्वेअर) की मदद से A और B पर लंबवत रेखाएँ खींचें।
A की लंबवत रेखा पर बिंदु P इस तरह चिह्नित करें कि AP = 8 सेमी हो।
B की लंबवत रेखा पर बिंदु Q इस तरह चिह्नित करें कि BQ = 8 सेमी हो।
अब रूलर की मदद से बिंदु P और Q को जोड़ें।
अंत में P और Q से ऊपर की अतिरिक्त रेखाएँ मिटा दें।

चरण 2. रूलर से बिंदु C, D, E और F ऐसे चिन्हित करें कि AC = 4 सेमी, BD = 4 सेमी, QE = 4 सेमी और PF = 4 सेमी हों।
अब C को E से और F को D से जोड़ें। (आकृति 2)

चरण 3. माना कि रेखाएँ FD और CE बिंदु G पर कटती हैं।
अब वर्ग ACGF, CBDG, DQEG और GEPF के विकर्ण खींचकर उनके केंद्र बिंदु ज्ञात करें।

चरण 4. वृत्तों के केंद्र ज्ञात करने में उपयोग की गई अतिरिक्त रेखाएँ मिटा दें।
फिर, चारों छोटे वर्गों के केंद्रों पर केंद्र रखते हुए 1.3 सेमी त्रिज्या से चार वृत्त बनाएँ।

चरण 5. आकृति 4 अभीष्ट चार छेदों वाला वर्ग है।

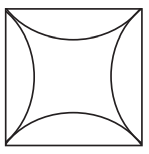
6. वक्रों वाला वर्ग
यह 8 सेमी की भुजा का एक वर्ग है।
[संकेत-सोचिए कि परकार के नुकीले सिरे को कहाँ रखा जाए ताकि चारों चाप (arc) प्रत्येक भुजा से समान रूप से उभरें। प्रयत्न कीजिए।

उत्तर: 

चरण 1: रूलर से 8 सेमी लंबी रेखा AB खींचें।
चांदा (सेट स्क्वेअर) से A और B पर लंब रेखाएँ बनाएं।
A की लंब रेखा पर AP = 8 सेमी तक बिंदु P चिह्नित करें।
B की लंब रेखा पर BQ = 8 सेमी तक बिंदु Q चिह्नित करें।
अंत में P और Q के ऊपर की अतिरिक्त रेखाएँ मिटा दें।

चरण 2: रूलर से बिंदु C, D, E और F इस प्रकार चिह्नित करें कि AC = 4 सेमी, BD = 4 सेमी, QE = 4 सेमी और PF = 4 सेमी हो।
अब C को E से और D को F से रेखाओं द्वारा जोड़ें।
इन रेखाओं को वर्ग के बाहर तक बढ़ाएँ।

चरण 3: DF रेखा को बढ़ाकर उस पर बिंदु G और H लें, जिससे DG और FH = 4 सेमी हों
CE रेखा को बढ़ाकर उस पर बिंदु I और J लें, जिससे CI और EJ = 4 सेमी हों।
अंत में बिंदु B और G को जोड़ें।

चरण 4: G, H, I और J को केंद्र मानकर, BG के बराबर त्रिज्या से वर्ग के अंदर चार चाप खींचें (जैसे आकृति में दिखाया गया है)।
अब सभी अतिरिक्त रेखाएँ मिटा दें।

चरण 5. आकृति 4, “वक्रों वाला वर्ग” की अभीष्ट आकृति है।

रचना कीजिए (Page – 211)

1. एक आयत की रचना कीजिए जिसमें एक विकर्ण सम्मुख कोणों को 50° और 40° में विभाजित करता हो।

उत्तर: हम आकृति 1 में दिखाए गए रूप का एक आयत बनाएँगें।

चरण 1: रूलर की सहायता से 4 सेमी लंबी एक रेखा AB खींचें।

चरण 2: चाँदे का केंद्रीय बिंदु A पर रखते हुए, 50° और 90° (50° + 90°) पर बिंदु C और D को चिह्नित करें।

चरण 3. एक चाँदे का उपयोग करके AB के B पर एक लंब रेखा खींचें और इसे E तक विस्तारित रेखा AC को प्रतिच्छेद करने दें। (आकृति 3)

चरण 4. चाँदे का प्रयोग करके BE के E पर एक लंब रेखा खींचें और इसे विस्तारित रेखा AD को F पर प्रतिच्छेदित करें।

चरण 5. आकृति 4 में अतिरिक्त रेखाओं को मिटा दें।

चरण 6. आकृति 5 वह अभीष्ट आयत है जिसमें एक विकर्ण सम्मुख कोणों को 50° और 40° में विभाजित करता है।

3. एक आयत की रचना कीजिए जिसकी एक भुजा 4 सेमी है और विकर्ण की लंबाई 8 सेमी है।

उत्तर: हम आकृति 1 में दिखाए गए रूप का एक आयत बनाएंगे।

चरण 1. एक रूलर का उपयोग करके 4 सेमी की एक रेखा AB खीचें।

चरण 2. एक चाँदे का उपयोग करके AB पर A और B लंब रेखा खींचें।

चरण 3: A को केंद्र और 8 सेमी त्रिज्या लेकर एक चाप खींचें जो लंब रेखा को B की ओर काटे।
फिर B को केंद्र और 8 सेमी त्रिज्या लेकर एक चाप खींचें जो लंब रेखा को A की ओर काटे।

चरण 4. चापों के प्रतिच्छेद बिंदुओं को PQ से मिलाए।

चरण 5. आकृति 5 में अतिरिक्त रेखाओं को मिटा दें।

चरण 6. आकृति 6 अभीष्ट आयत है। जिसकी एक भुजा 4 सेमी है और विकर्णों की लंबाई 8 सेमी है।

रचना कीजिए (Page 215)

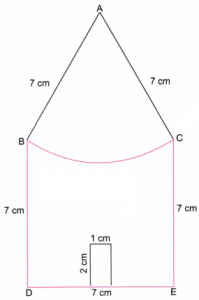
1. इससे बड़े एक घर का निर्माण कीजिए जिसकी सभी भुजाएँ 7 सेमी लंबी हों।

उत्तर: 

चरण 1. रूलर की सहायता से 7 सेमी लंबी रेखा DE खींचें।

चरण 2: चाँदे की सहायता से D और E पर DE के लंबवत रेखाएँ खींचें।
D पर लंबवत रेखा पर बिंदु B चिह्नित करें जहाँ BD = 7 सेमी हो।
E पर लंबवत रेखा पर बिंदु C चिह्नित करें जहाँ CE = 7 सेमी हो।

चरण 3: 7 सेमी – 1 सेमी = 6 सेमी, और 6 ÷ 2 = 3 सेमी।
रूलर से DE पर बिंदु P और Q इस प्रकार चिह्नित करें कि DP = 3 सेमी और QE = 3 सेमी हो।
चाँदे की सहायता से D और E पर बिंदु P और Q से होकर 2 सेमी लंबी लंब रेखाएँ खींचें।

चरण 4: बिंदु R और S को रेखा से जोड़ें।
B और C को केंद्र मानकर 7 सेमी त्रिज्या से ऐसे चाप खींचें जो बिंदु A पर प्रतिच्छेद करें।
अब AB और AC को जोड़ें।
फिर A को केंद्र मानकर 7 सेमी त्रिज्या से B से C तक एक चाप खींचें।
अंत में सभी अतिरिक्त रेखाएँ मिटा दें।

चरण 5: आकृति 4 ही वांछित घर की पुनर्निर्मित आकृति है, जिसमें सभी भुजाएँ 7 सेमी लंबी हैं और वे मिलकर घर की सीमा बनाती हैं।

2. घर की रचना में सम्मिलित संकल्पनाओं का प्रयोग करते हुए, सेक्शन कलाकृति से ‘एक व्यक्ति’, ‘तरंगित लहर’ और ‘आँखें’ का पुनः सृजन करने का प्रयास करें।

उत्तर: स्वयं करें।

3. क्या चार समान भुजाओं वाली एक आकृति बनाई जा सकती है, जो वर्ग न हो? यदि ऐसी आकृति का अस्तित्व है, तो क्या आप इसकी रचना कर सकते हैं?

उत्तर: चरण 1. एक रेखा खींचें और उस पर बिंदु A और B इस प्रकार चिह्नित करें कि AB = 5 सेमी हो (मान लें)।

चरण 2: चाँदे की मदद से बिंदु A और B पर उनके दाईं ओर 60° के कोण बनाते हुए बिंदु C और D चिह्नित करें।

चरण 3: रूलर से AC पर बिंदु P लें ताकि AC = 5 सेमी हो, और BD पर बिंदु Q लें ताकि BD = 5 सेमी हो। फिर P और Q को रेखा से जोड़ें।

चरण 4: रूलर से दूरी PQ मापें। यदि PQ = 5 सेमी है, तो भी ∴ ABQP एक वर्ग नहीं है।

चरण 5: यह दर्शाता है कि कुछ चतुर्भुज ऐसे होते हैं जिनकी चारों भुजाएँ बराबर होती हैं, फिर भी वे वर्ग नहीं होते।