Question Answer For All Chapters – गणित प्रकाश Class 6th
सममिति
आइए, पता लगाएँ (Page – 219)
1. क्या आप इस अध्याय के प्रारंभ में दी गई आकृतियों में सममिति की रेखा देख पाए हैं? बादलों की आकृति के विषय में आपका क्या विचार है?
उत्तर: फूल में 6 सममिति की रेखाएँ हैं।
तितली में 1 सममिति की रेखा है।
रंगोली में 4 सममिति की रेखाएँ हैं।
चक्कीदार पंखा (पिनव्हील) में कोई सममिति की रेखा नहीं है।
बादल में सममिति की रेखा हो भी सकती है और नहीं भी, क्योंकि उसका आकार स्थिर नहीं होता।
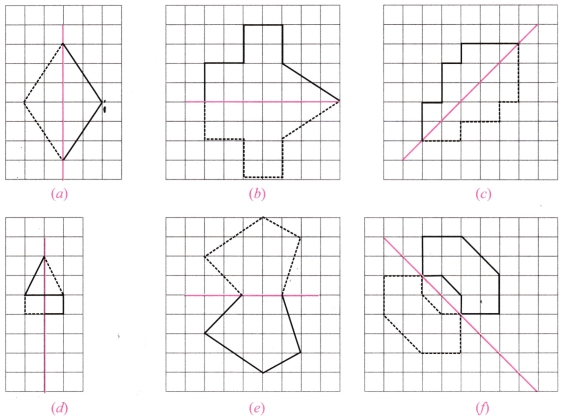
2. निम्न आकृतियों में यदि सममिति की रेखाएँ हैं, तो उन्हें पहचानिए।
उत्तर:
एक से अधिक सममिति रेखाओं वाली आकृतियाँ ऐसी होती हैं जिनमें किसी भी रेखा के अनुसार उसे मोड़ने पर दोनों भाग आपस में पूरी तरह मेल खाते हैं। ऐसी आकृतियों को परावर्तीय सममिति (Reflection Symmetry) वाली आकृतियाँ कहा जाता है।
इन आकृतियों को कागज को अलग-अलग तरीकों से मोड़कर, फिर उसे काटकर या पंचिंग मशीन से छेद करके आसानी से बनाया जा सकता है। ऐसे प्रयोगों से सममिति की समझ और गहराई से विकसित होती है।
आइए, पता लगाएँ (Page 223 – 230)
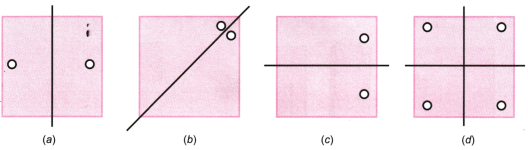
1. दी गई प्रत्येक आकृति में कागज की मुड़ी हुई चौकोर शीट में एक छेद किया गया है और फिर कागज को खोल दिया गया है। उस रेखा की पहचान कीजिए जिसके साथ कागज को मोड़ा गया था।
चित्र (d) एक छेद करके बनाया गया है। ज्ञात कीजिए कागज को कैसे मोड़ा गया था।
उत्तर:
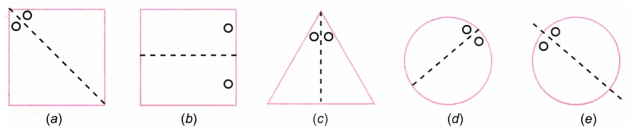
2. सममिति रेखाएँ दी गई हैं, अन्य छेदों को ज्ञात कीजिए-
उत्तर:
3. नीचे कागज काटने से संबंधित कुछ प्रश्न दिए गए हैं।
एक ऊर्ध्वाधर मोड़ पर विचार कीजिए। उसे हम निम्न प्रकार से दर्शाते हैं-
इसी प्रकार, क्षैतिज मोड़ को निम्न प्रकार से दर्शाते हैं।
उत्तर:
4. नीचे दी गई प्रत्येक स्थिति में काटने के पश्चात् जब कागज को खोला जाए तब छेद के आकार का अनुमान लगाकर उसे सत्यापित कीजिए।
उत्तर:
5. मान लीजिए कि आपको इनमें से प्रत्येक आकार को कुछ मोड़ों और एक सीधे कट के साथ प्राप्त करना है। आप ऐसा किस प्रकार करेंगे?
(a) केंद्र में स्थित छेद एक वर्ग है।
उत्तर:
(b) केंद्र में स्थित छेद एक वर्ग है।
उत्तर:
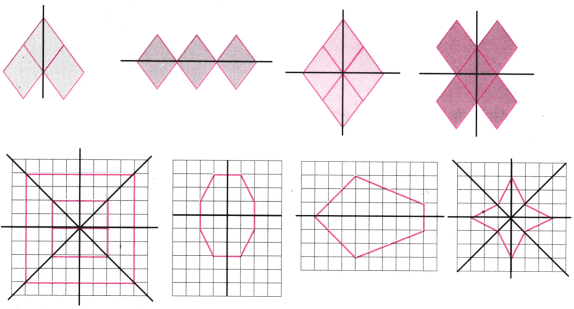
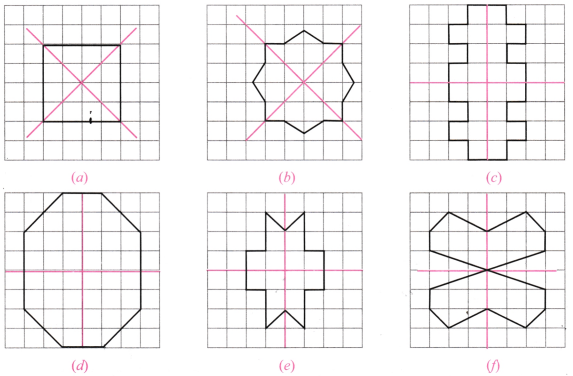
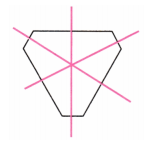
6. इन आकृतियों में कितनी सममिति की रेखाएँ हैं?
उत्तर:
7. प्रत्येक आकृति का अक्स बनाइए तथा सममिति की रेखाएँ खींचिए, यदि कोई है तो-
उत्तर:
8. नीचे दिए गए कोलम में सममिति की रेखाएँ ज्ञात कीजिए-
उत्तर:
9. निम्नलिखित का चित्र बनाइए-
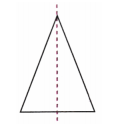
(a) एक त्रिभुज जिसमें सममिति की केवल एक रेखा हो।
(b) एक त्रिभुज जिसमें सममिति की केवल तीन रेखाएँ हों।
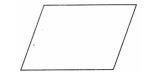
(c) एक त्रिभुज जिसमें सममिति की कोई रेखा ना हो।
क्या ठीक दो सममिति रेखाओं का त्रिभुज बनाना संभव है?
उत्तर:
10. निम्नलिखित का चित्र बनाइए । प्रत्येक स्थिति में, आकृति में कम-से-कम एक घुमावदार सीमा अवश्य हो ।
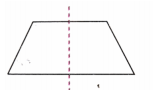
(a) ठीक एक सममिति की रेखा वाला चित्र
(b) ठीक दो सममिति की रेखाओं वाला चित्र
(c) ठीक चार सममिति की रेखाओं वाला चित्र
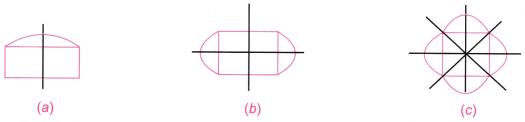
11. निम्नलिखित आकृतियों को एक वर्गाकार कागज पर बनाइए। उन्हें इस प्रकार पूरा कीजिए कि काले रंग की रेखा सममिति की रेखा हो । समस्या (a) को आपके लिए पूरा किया गया है।
उत्तर:
12. निम्नलिखित आकृतियों को एक वर्गाकार कागज पर बनाइए। उनमें से प्रत्येक को इस प्रकार पूरा कीजिए कि परिणामी आकृति में सममिति की रेखाओं के रूप में दो काली रेखाएँ हो।
उत्तर:
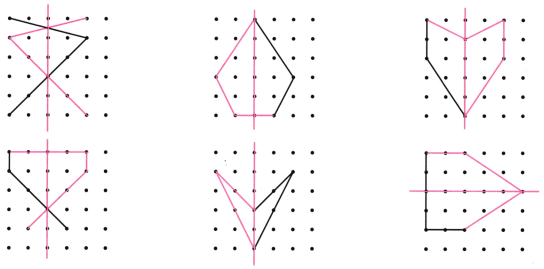
13. निम्नलिखित रेखा आकृतियों को डॉट ग्रिड पर बनाइए । प्रत्येक आकृति के लिए दो और रेखाएँ खींचिए ताकि ऐसी एक आकृति बन सके, जिसमें सममिति की एक रेखा हो।
उत्तर:
आइए, पता लगाएँ (Page 235 – 236)
1. दी गई आकृतियों में दिए गए चिह्न के परित समिमित के कोण ज्ञात कीजिए।
उत्तर: सममिति का कोण जानने के लिए आकृति को 90° पर घुमाकर देखें।
आकृति 90° पर घुमाने पर वैसी ही दिखती है, इसलिए 90° इसका सममिति कोण है।
90° घूमने पर उपरोक्त आकृति बनती है। मूल आकृति के साथ अतिव्यापी नहीं होती है। यह आकृति 360° के एक पूर्ण चक्कर के बाद ही अपने मूल आकार में वापस आती है। इसलिए 360° सममिति का कोण है।
180° घूमने के बाद आकृति बिल्कुल वैसी ही रहती है। इसलिए 180° सममिति का कोण है।
2. निम्नलिखित में से किस आकृति में एक से अधिक सममिति के कोण हैं?
उत्तर: आकृति (g) को छोड़कर सभी आकृतियों में एक से अधिक सममिति के कोण हैं।
3. प्रत्येक आकृति के लिए घूर्णन सममिति का क्रम बताइए-
(a)
उत्तर: 2
(b)
उत्तर: 1
(c)
उत्तर: 6
(d)
उत्तर: 3
(e)
उत्तर: 4
(f)
उत्तर: 5
आइए, पता लगाएँ (Page 238 – 239)
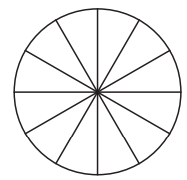
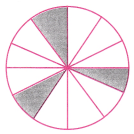
1. नीचे दिए गए वृत्त के त्रिज्याखंडों में इस प्रकार रंग भरिए कि आकृति में
(a) 3 सममिति के कोण हों।
(b) 4 सममिति के कोण हों।
(c) सममिति के संभव कोणों की संख्या क्या होगी ? यदि इन त्रिज्याखंडों को अलग-अलग रंगों से अलग-अलग विधियों द्वारा भरा जाए तो,
उत्तर: (a) यह आकृति हर 120° के घुमाव पर समान दिखाई देती है।
(b) यह आकृति हर 90° के घुमाव पर समान दिखाई देती है।
(c) चार तरीके संभव हैं
2. वृत्त और वर्ग को छोड़कर, ऐसी अन्य दो आकृतियाँ बनाइए, जिनमें परावर्तीय सममिति और घूर्णन सममिति दोनों हों।
उत्तर:
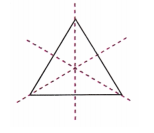
3. जहाँ भी संभव हो, निम्नलिखित का एक कच्चा स्कैच खींचिए-
(a) एक त्रिभुज, जिसमें न्यूनतम दो सममिति की रेखाएँ हों तथा न्यूनतम दो सममिति के कोण हों।
उत्तर:
(b) एक त्रिभुज, जिसमें केवल एक सममिति की रेखा हो लेकिन कोई घूर्णन सममिति न हो।
उत्तर:
(c) घूर्णन सममिति वाला ऐसा चतुर्भुज, जिसमें कोई परावर्तीय सममिति न हो।
उत्तर:
(d) एक परावर्तीय सममिति वाला चतुर्भुज, जिसमें कोई घूर्णन सममिति न हो।
उत्तर:
4. एक आकृति में सममिति का न्यूनतम कोण 60° है। इस आकृति के अन्य सममिति के कोण क्या हैं?
उत्तर: यदि किसी आकृति में सममिति का न्यूनतम कोण 60° है, तो उसके अन्य सममिति के कोण 60° के गुणज होंगे।
इसलिए सममिति के अन्य कोण होंगे:
60°, 120°, 180°, 240°, 300°, और 360°।
5. एक आकृति में एक सममिति का कोण 60° है। इस आकृति के दो सममिति के कोण 60° से कम हैं। सममिति का न्यूनतम कोण क्या होगा?
उत्तर: सममिति का न्यूनतम कोण = 60° ÷ 3 = 20°.
6. क्या हम घूर्णन सममिति के साथ एक ऐसी आकृति प्राप्त कर सकते हैं, जिसमें सममिति का न्यूनतम कोण
(a) 45° है?
(b) 17° है?
उत्तर: (a) हाँ, क्योंकि 360°, 45° से विभाज्य है।
(b) नहीं, क्योंकि 360°, 17° से विभाज्य नहीं है।
7. यह दिल्ली में स्थित नए संसद भवन का चित्र है-
(a) क्या इस चित्र की बाहरी परिसीमा ( boundary) में परावर्तन सममिति है? यदि ऐसा है, तो सममिति की रेखाएँ खींचिए । वे कितनी हैं ?
उत्तर: बाहरी सीमा में केंद्र के चारों ओर घूर्णन सममिति दिखाई देती है।
घूर्णन का सबसे छोटा कोण है: 360° ÷ 3 = 120°
अन्य घूर्णन कोण हैं: 240° और 360°
(b) क्या इसकी अपने केंद्र के परित घूर्णन सममिति है? यदि ऐसा है, तो घूर्णन सममिति के कोण ज्ञात कीजिए।
उत्तर: बाहरी सीमा में परावर्तीय सममिति (प्रतिबिंब सममिति) दिखाई देती है।
इसमें 3 सममिति रेखाएँ हैं।
8. अध्याय 1, सारणी 3 में पहले आकृति अनुक्रम नियमित बहुभुज आकार अनुक्रम आकृतियों में सममिति की कितनी रेखाएँ हैं? आपको कौन-सा संख्या अनुक्रम मिलता है।
उत्तर:
3 भुजाओं वाले समबाहु त्रिभुज में 3 रेखाएँ सममिति की होती हैं।
4 भुजाओं वाले वर्ग में 4 सममिति रेखाएँ होती हैं।
5 भुजाओं वाले सम पंचभुज में 5 सममिति रेखाएँ होती हैं।
6 भुजाओं वाले सम षट्भुज में 6 सममिति रेखाएँ होती हैं।
इससे यह नियम स्पष्ट होता है कि:
“सम बहुभुज में जितनी भुजाएँ होती हैं, उतनी ही सममिति की रेखाएँ होती हैं।”
इस प्रकार भुजाओं और सममिति रेखाओं की संख्या का अनुक्रम है: 3, 4, 5, 6…..
9. अध्याय 1 की सारणी 3 में पहले आकृति अनुक्रम नियमित बहुभुज के आकार अनुक्रम की आकृतियों में सममिति के कितने कोण हैं? आपको कौन-सा संख्या अनुक्रम प्राप्त होता है?
उत्तर:
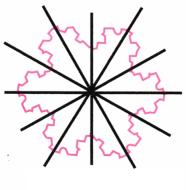
10. अध्याय 1 की सारणी 3 में अंतिम आकृति अनुक्रम कोच स्नोफ्लेक के आकार अनुक्रम में आकृतियों में सममिति की कितनी रेखाएँ है? सममिति के कितने कोण हैं?
उत्तर: अशोक चक्र में कुल 24 तीलियाँ होती हैं जो बराबर दूरी पर स्थित होती हैं।
इन 24 तीलियों से 12 विपरीत जोड़े बनते हैं।
हर एक विपरीत जोड़ा एक सममिति की रेखा दर्शाता है।
इसलिए अशोक चक्र में कुल 12 सममिति रेखाएँ होती हैं।
सबसे छोटा सममिति कोण = 360° ÷ 12 = 30°
अन्य सममिति कोण 30° के गुणक होते हैं जैसे:
30°, 60°, 90°, 120°, 150°, 180°, 210°, 240°, 270°, 300°, 330°, 360°
इस प्रकार कुल 12 सममिति कोण प्राप्त होते हैं।







































Class 6 math