Question Answer For All Chapters – गणित प्रकाश Class 6th
गणित में पैटर्न
1.1 आइए, पता लगाएँ (Page 2)
1. क्या आप अन्य उदाहरण सोच सकते हैं जहाँ गणित हमारी रोजमर्रा की ज़िंदगी में मदद करता है?
उत्तर:हां, जैसे:
- बजट बनाना और पैसे गिनना
- समय देखना और समय सारिणी बनाना
- रसोई में माप और अनुपात का उपयोग
- मोबाइल और कंप्यूटर का काम करना
- रास्ता तय करने के लिए दिशा और दूरी मापना
2. गणित ने किस प्रकार मानव को आगे बढ़ाने के लिए प्रेरित करने में सहायता की है? (आप उन उदाहरणों के विषय में विचार कर सकते हैं जिनमें वैज्ञानिक प्रयोग करना; अपनी अर्थव्यवस्था और लोकतंत्र को चलाना; पुलों, घरों या अन्य जटिल भवनों को निर्मित करना; टी.वी., मोबाइल फोन, कम्प्यूटरों, साइकिलों, रेलगाड़ियों, कारों, वायुयानों, कैलेंडरों, घड़ियों इत्यादि को बनाना सम्मिलित हैं।)
उत्तर: गणित ने मानव समाज को अनेक क्षेत्रों में आगे बढ़ने के लिए प्रेरित किया है। कुछ प्रमुख उदाहरण इस प्रकार हैं:
- वैज्ञानिक प्रयोगों में सहायता:
गणितीय सूत्रों और आँकड़ों की मदद से वैज्ञानिक प्रयोग सटीक और सफल होते हैं। जैसे—चंद्रमा और मंगल मिशन। - अर्थव्यवस्था और लोकतंत्र को चलाने में:
बजट, कर-गणना, जनगणना, मतदान आँकड़े, आदि गणित के बिना असंभव हैं। - इमारतों और पुलों का निर्माण:
निर्माण कार्य में मापन, अनुपात, कोण और क्षेत्र की गणना जरूरी होती है, जो गणित के बिना संभव नहीं। - तकनीकी उपकरणों का निर्माण:
टी.वी., मोबाइल फोन, कम्प्यूटर, इंटरनेट—इन सबकी तकनीकी संरचना में गणित की भूमिका अहम है। - परिवहन के साधन:
साइकिल, रेलगाड़ी, कार, वायुयान—इनकी गति, दूरी, ईंधन गणना आदि में गणित का प्रयोग होता है।
1.2 आइए, पता लगाएँ (Page 2)
1. क्या आप सारणी 1 में दिए प्रत्येक अनुक्रम में पैटर्न की पहचान कर सकते हैं?
1, 1, 1, 1, 1, 1, 1,…. (सभी ‘1’)
1, 2, 3, 4, 5, 6, 7, …. (गणन संख्याएँ)
1, 3, 5, 7, 9, 11, 13, …. (विषम संख्याएँ)
2, 4, 6, 8, 10, 12, 14, …. (सम संख्याएँ)
1, 3, 6, 10, 15, 21, 28, …. (त्रिभुजाकार संख्याएँ)
1, 4, 9, 16, 25, 36, 49, …. (वर्ग संख्याएँ)
1, 8, 27, 64, 125, 216, …. (घन संख्याएँ)
1, 2, 3, 5, 8, 13, 21, …. (विरहांक संख्याएँ)
1, 2, 4, 8, 16, 32, 64, …. (2 की घातें)
1, 3, 9, 27, 81, 243, 729, …. (3 की घातें)
उत्तर: हाँ, हर क्रम में एक विशेष नियम है जैसे:
- सम संख्या में 2 जोड़ते जाना
- विषम संख्याओं में 2 का अंतर
- घन, वर्ग, आदि में उनके नियम, इत्यादि…..
2. सारणी 1 में दिए प्रत्येक अनुक्रम को उसकी अगली तीन संख्याओं सहित अपनी नोटबुक पर पुनः लिखिए। प्रत्येक अनुक्रम के बाद, उस अनुक्रम में संख्याओं को बनाने वाले नियम को अपने शब्दों में लिखिए।
- 1. सभी 1 वाली संख्याएँ (All 1’s):
- अनुक्रम: 1, 1, 1, 1, 1, 1, 1, 1, 1, 1
नियम: हर संख्या 1 है। सभी संख्याएँ बराबर होती हैं।
- अनुक्रम: 1, 1, 1, 1, 1, 1, 1, 1, 1, 1
- 2. गणना संख्याएँ (Counting Numbers):
- अनुक्रम: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
नियम: हर अगली संख्या में 1 जोड़ा जाता है।
- अनुक्रम: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
- 3. विषम संख्याएँ (Odd Numbers):
- अनुक्रम: 1, 3, 5, 7, 9, 11, 13, 15, 17, 19
नियम: हर अगली संख्या में 2 जोड़ा जाता है। यह सभी संख्याएँ 2 से विभाज्य नहीं हैं।
- अनुक्रम: 1, 3, 5, 7, 9, 11, 13, 15, 17, 19
- 4. सम संख्याएँ (Even Numbers):
- अनुक्रम: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20
नियम: हर अगली संख्या में 2 जोड़ा जाता है। यह सभी संख्याएँ 2 से विभाज्य होती हैं।
- अनुक्रम: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20
- 5. त्रिकोणीय संख्याएँ (Triangular Numbers):
- अनुक्रम: 1, 3, 6, 10, 15, 21, 28, 36, 45, 55
- नियम: हर अगली संख्या में क्रमशः 2, 3, 4, 5… जोड़ते हैं।
जैसे:
1+2=3, 3+3=6, 6+4=10, …
- 6. वर्ग संख्याएँ (Square Numbers):
- अनुक्रम: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100
- नियम: हर संख्या किसी पूर्ण संख्या का वर्ग (गुणा) होती है:
1², 2², 3², …, 10²
- 7. घन संख्याएँ (Cube Numbers):
- अनुक्रम: 1, 8, 27, 64, 125, 216, 343, 512, 729
- नियम: हर संख्या किसी पूर्ण संख्या का घन होती है:
1³, 2³, 3³, …, 9³
- 8. विरहाङ्क संख्याएँ (Virahānka Numbers / Fibonacci Series):
- अनुक्रम: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89
- नियम: हर अगली संख्या पिछली दो संख्याओं का योग होती है:
1+2=3, 2+3=5, 3+5=8, …
- 9. 2 की घातें (Powers of 2):
- अनुक्रम: 1, 2, 4, 8, 16, 32, 64, 128, 256, 512
- नियम: हर अगली संख्या पिछले का दो गुना होती है।
या - \( 2^0 2^1, 2^2, …, 2^9 \)
- 10. 3 की घातें (Powers of 3):
- अनुक्रम: 1, 3, 9, 27, 81, 243, 729, 2187, 6561, 19683
- नियम: हर अगली संख्या पिछले का तीन गुना होती है।
या - \( 3^0, 3^1, 3^2, …, 3^9\)
1.3 आइए, पता लगाएँ (Page 5,6)
1. सारणी 2 में दिए संख्या अनुक्रमों को चित्रात्मक रूप से दर्शाने के लिए अपनी नोटबुक में प्रतिलिपि बनाकर प्रत्येक अनुक्रम के लिए अगला चित्र बनाइए।
2. 1,3,6, 10, 15, … त्रिभुजाकार संख्याएँ क्यों कहलाती हैं? 1, 4, 9, 16, 25, … वर्ग संख्याएँ या वर्ग क्यों कहलाती हैं? 1, 8, 27, 64, 125, … घन संख्याएँ या घन क्यों कहलाती हैं?
उत्तर:
- (क) 1, 3, 6, 10, 15, … त्रिकोणीय संख्याएँ (Triangular Numbers)
क्योंकि इन संख्याओं को बिंदुओं के रूप में इस तरह सजाया जा सकता है कि वे एक पूर्ण त्रिभुज (Triangle) का आकार बनाते हैं। - (ख) 1, 4, 9, 16, 25, … वर्ग संख्याएँ (Square Numbers)
क्योंकि इन संख्याओं को बिंदुओं की मदद से इस प्रकार सजाया जा सकता है कि वे एक पूर्ण वर्ग (Square) की आकृति बनाते हैं। - (ख) 1, 4, 9, 16, 25, … वर्ग संख्याएँ (Square Numbers)
क्योंकि इन संख्याओं को बिंदुओं की मदद से इस प्रकार सजाया जा सकता है कि वे एक पूर्ण वर्ग (Square) की आकृति बनाते हैं।
3. आपने ध्यान दिया होगा कि 36 एक त्रिभुजाकार संख्या और वर्गाकार संख्या दोनों है। अर्थात् 36 बिंदुओं को त्रिभुज और वर्ग दोनों में पूरी तरह व्यवस्थित किया जा सकता है। इसे स्पष्ट करते हुए अपनी नोटबुक में चित्र बनाइए।
इससे ज्ञात होता है कि एक ही संख्या को अलग-अलग तरीकों से दर्शाया जा सकता है और संदर्भ के आधार पर अलग-अलग भूमिकाएँ निभाई जा सकती हैं। कुछ अन्य संख्याओं को अलग-अलग तरीकों से चित्रात्मक रूप से दर्शाने का प्रयास कीजिए।
उत्तर:
1225 = 35 × 35
यह एक पूर्ण वर्ग संख्या है, क्योंकि इसे वर्ग के रूप में 35 पंक्तियों और 35 स्तंभों में बिंदुओं से दर्शाया जा सकता है।
4. आप संख्याओं के निम्नलिखित अनुक्रम को क्या कहेंगे?
इन्हें षड्भुजाकार (hexagonal) संख्याएँ कहते हैं। इन्हें अपनी नोटबुक में बनाइए। अनुक
में अगली संख्या क्या होगी?
उत्तर: अगली संख्या (37 + 4 × 6) = 61 है।
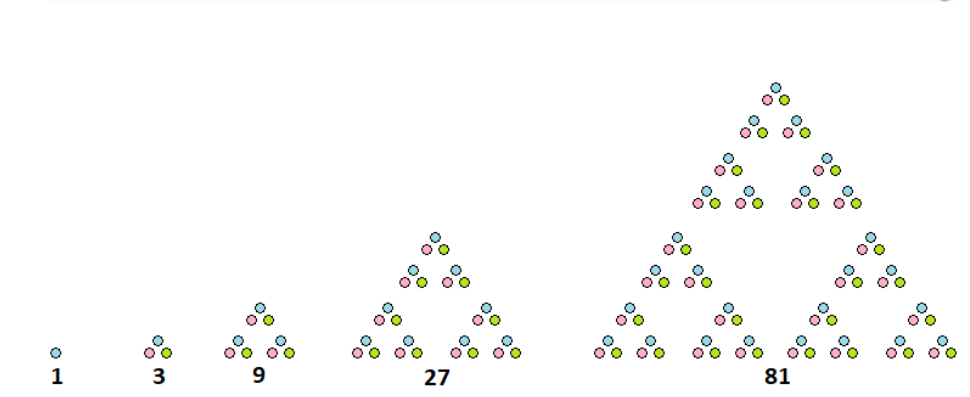
5. क्या आप ‘2 की घात’ के अनुक्रम का चित्रीय निरूपण कर सकते हैं? ‘3 की घात’ का?
उत्तर:
1.4 आइए, पता लगाएँ (Page 8,9)
1. गणन संख्याओं को ऊपर और नीचे जोड़ने पर अर्थात् 1, 1 + 2 + 1, 1 + 2 + 3 + 2 + 1,…, से वर्ग संख्याएँ क्यों प्राप्त होती हैं, क्या आप इसके लिए एक चित्रीय स्पष्टीकरण दे सकते हैं?
उत्तर: गणन संख्याओं को जोड़ने पर हमें वर्ग संख्याएँ प्राप्त होती हैं क्योंकि जब हम 1,1+2,1+2+3 जोड़ते हैं, तो यह एक वर्ग के आकार का निर्माण करता है। उदाहरण के लिए, 1 एक बिंदु है, 1+2 एक रेखा है, और 1+2+3 एक त्रिकोण है। जब हम इन त्रिकोणों को जोड़ते हैं, तो हमें एक वर्ग मिलता है।
1= \( 1^2 \)
1+2=3=\( 2^2 \) −1
1+2+3=6=\( 3^2 \) −3
2. इस तस्वीर के बड़े संस्करण की कल्पना करके या आवश्यकतानुसार उसका आंशिक चित्र बनाकर, क्या आप ज्ञात कर सकते हैं कि 1 + 2 + 3 + … + 99+ 100 + 99 + … + 3 + 2 + 1 का मान क्या होगा?
उत्तर:
1 + 2 + 1 = 4
1 + 2 + 3 + 2 + 1 = 9
1 + 2 + 3 + 4 + 3 + 2 + 1 = 16
1 + 2 + 3 + 4 + 5 + 4 + 3 + 2 + 1 = 25
1 + 2 + 3 + 4 + 5 + 6 + 5 + 4 + 3 + 2 + 1 = 36
.
.
1 + 2 + 3 + … + 99 + 100 + 99 + … + 3 + 2 + 1 = 10000
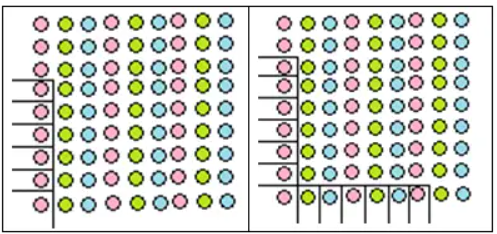
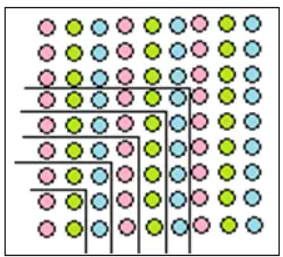
3. जब आप सभी ‘1’ वाले अनुक्रम को ऊपर की ओर जोड़ना प्रारंभ करते हैं, तब आपको कौन-सा अनुक्रम प्राप्त होता है? जब आप सभी ‘1’ वाले अनुक्रम को ऊपर और नीचे जोड़ते हैं, तब कौन-सा अनुक्रम प्राप्त होता है?
उत्तर:
जब हम सभी ‘1’ वाली श्रेणी को ऊपर की ओर जोड़ते हैं, तो हमें गणना संख्याओं (Counting Numbers) की श्रेणी प्राप्त होती है।(पहला चित्र)
जब हम सभी ‘1’ वाली श्रेणी को ऊपर और नीचे दोनों ओर जोड़ते हैं, तो हमें विषम संख्याओं (Odd Numbers) की श्रेणी प्राप्त होती है।(दूसरा चित्र)
4. जब आप गणन संख्याओं को ऊपर की ओर जोड़ना प्रारंभ करते हैं, तब आपको कौन-सा अनुक्रम प्राप्त होता है? क्या आप एक छोटे से चित्र के माध्यम से स्पष्टीकरण दे सकते हैं?
उत्तर: जब हम गणन संख्याओं को ऊपर की ओर जोड़ते हैं, तो हमें एक त्रिकोणीय अनुक्रम प्राप्त होता है।
यह अनुक्रम 1,3,6,10,… है। इसे चित्र द्वारा स्पष्ट किया जा सकता है।
5. जब आप क्रमागत त्रिभुजाकार संख्याओं के युग्मों को जोड़ते हैं तब क्या होता है? उदाहरण के लिए, 1 + 3,3 + 6, 6+10, 10+15,… को लीजिए। आप कौन-सा अनुक्रम मिलता है? क्यों? क्या आप इसे एक चित्र द्वारा स्पष्ट कर सकते हैं?
उत्तर: जब हम क्रमागत त्रिभुजाकार संख्याओं के युग्मों को जोड़ते हैं, तो हमें एक नया अनुक्रम मिलता है।
1+3=4, 3+6=9, 6+10=16, 10+15=25, यह अनुक्रम 4,9,16,25 है, जो वर्ग संख्याएँ हैं।
वर्ग संख्याएँ: 4,9,16,25.
6. जब आप 1 से प्रारंभ करते हुए 2 की घातों को जोड़ना प्रारंभ करते हैं तब क्या होता है? उदाहरण के लिए, 1, 1+2, 1+2+4,1+2+4+8,… लीजिए? अब, इनमें से प्रत्येक संख्या में 1 जोड़ दीजिए- आप कौन-सी संख्याएँ प्राप्त करते हैं? ऐसा क्यों होता है?
1
1 + 2 = 3
1 + 2 + 4 = 7
1 + 2 + 4 + 8 = 15
1 + 2 + 4 + 8 + 16 = 31
अब, हर योग में 1 जोड़ें:
1 +1 = 2 = 2¹
3 +1 = 4 = 2²
7 +1 = 8 = 2³
15 +1 = 16 = 2⁴
31 +1 = 32 = 2⁵
आपको मिलती हैं: 2, 4, 8, 16, 32…
यह हैं: 2 की घातें (powers of 2)
7. जब आप त्रिभुजाकार संख्याओं को 6 से गुणा करते हैं और 1 जोड़ते हैं तो क्या होता है? आपको कौन-सा अनुक्रम मिलता है? क्या आप इसे चित्र के माध्यम से समझा सकते हैं?
उत्तर:
| त्रिभुज संख्या | × 6 | + 1 | उत्तर |
|---|---|---|---|
| 1 | 6 | +1 | 7 |
| 3 | 18 | +1 | 19 |
| 6 | 36 | +1 | 37 |
| 10 | 60 | +1 | 61 |
यह षट्भुजात्मक संख्याओं (Hexagonal Numbers) का क्रम बनाता है: 7, 19, 37,……..
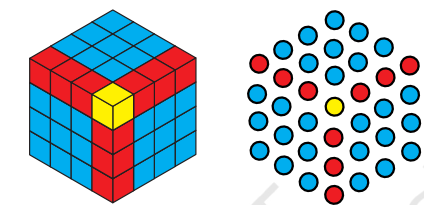
8. जब आप षड्भुजाकार संख्याओं को जोड़ना प्रारंभ करते हैं तब क्या होता है? उदाहरण के लिए, 1, 1 + 7, 1 + 7 + 19, 1 + 7 +19 + 37,… लीजिए? आप कौन-सा अनुक्रम प्राप्त करते हैं? क्या आप इसे एक घन के चित्र का उपयोग करते हुए स्पष्ट कर सकते हैं?
उत्तर:
| जोड़ | उत्तर |
|---|---|
| 1 | 1 |
| 1 + 7 | 8 |
| 1 + 7 + 19 | 27 |
| 1 + 7 + 19 + 37 | 64 |
| 1 + 7 + 19 + 37 + 61 | 125 |
हमें प्राप्त होती है संख्याएँ:
1, 8, 27, 64, 125, …
ये हैं: घन संख्याएँ (Cube Numbers)
= 1³, 2³, 3³, 4³, 5³, …
9. सारणी 1 में दिए गए अनुक्रमों में और दो भिन्न भिन्न अनुक्रमों के उनके बीच स्वयं अपनी ओर से अन्य पैटर्न या संबंध खोजिए। क्या एक चित्र या किसी अन्य माध्यम से आप यह स्पष्ट कर सकते हैं कि ऐसा क्यों होता है?
उत्तर: 3, 6, 9, 12, 15, 18,……… (3 के क्रमागत गुणज).
10, 15, 20, 25,…….. (प्रथम संख्या 10 है। इसके बाद प्रत्येक पद में 5 की वृद्धि होती है।)
1.5 आइए, पता लगाएँ (Page 11)
1. क्या आप सारणी 3 के प्रत्येक अनुक्रम में पैटर्न की पहचान कर सकते हैं?
उत्तर:
1. सम बहुभुज (Regular Polygons):
तिपृष्ठ (Triangle), चतुर्भुज (Square), पंचभुज (Pentagon), षट्भुज (Hexagon), सप्तभुज (Heptagon), अष्टभुज (Octagon), नवभुज (Nonagon), दशभुज (Decagon)
पैटर्न: प्रत्येक आकृति में एक भुजा (side) बढ़ रही है।
क्रमशः 3, 4, 5, 6, 7, 8, 9, 10 भुजाएँ हैं।
सभी भुजाएँ और कोण समान होते हैं।
2. पूर्ण आलेख (Complete Graphs – K2, K3, K4, K5, K6):
पैटर्न: प्रत्येक आलेख में एक नई बिंदु जोड़ी जाती है।
हर बिंदु हर अन्य बिंदु से जुड़ा होता है।
रेखाओं की संख्या त्रिकोणीय संख्या की तरह बढ़ती है: K2 = 1 रेखा, K3 = 3, K4 = 6, K5 = 10, K6 = 15
3. ढेरित वर्ग (Stacked Squares):
पैटर्न: वर्गों का आकार क्रमशः बढ़ता है: 1×1, 2×2, 3×3, 4×4, 5×5
कुल वर्गों की संख्या: 1, 4, 9, 16, 25 → ये वर्ग संख्याएँ (Square Numbers) हैं।
4. ढेरित त्रिभुज (Stacked Triangles):
पैटर्न: त्रिकोणों की पंक्तियाँ बढ़ती हैं: 1 पंक्ति, 2 पंक्तियाँ, 3 पंक्तियाँ…
कुल त्रिभुज: 1, 3, 6, 10, 15 → ये त्रिकोणीय संख्याएँ (Triangular Numbers) हैं।
5. कोच हिमकण (Koch Snowflake):
पैटर्न: हर चरण में प्रत्येक रेखा को तीन भागों में बाँटा जाता है और बीच वाला भाग हटाकर दो रेखाएँ जोड़ी जाती हैं (जैसे “स्पीड ब्रेकर”)।
इससे आकृति अधिक जटिल होती जाती है। रेखाओं की कुल संख्या बढ़ती जाती है: 3, 12, 48, …
2. सारणी 3 के प्रत्येक अनुक्रम को अपनी नोटबुक में पुनः बनाने का प्रयास कीजिए। क्या आप प्रत्येक अनुक्रम में अगले आकार को खींच सकते हैं? क्यों और क्यों नहीं? प्रत्येक अनुक्रम के बाद, अपने शब्दों में उस नियम या पैटर्न की व्याख्या कीजिए, जिसके अनुसार उस अनुक्रम में आकार बन रहे हैं।
उत्तर:
1. सम बहुभुज (Regular Polygons):
आकृतियाँ: त्रिभुज, चतुर्भुज, पंचभुज, षट्भुज, सप्तभुज, अष्टभुज, नवभुज, दशभुज
अगला होगा “एकादशभुज” (11 भुजाओं वाला सम बहुभुज)
नियम:
हर आकृति में एक भुजा की वृद्धि हो रही है। सभी भुजाएँ समान लंबाई की होती हैं और कोण भी बराबर होते हैं।

2. पूर्ण आलेख (Complete Graphs – K2, K3, K4, K5, K6):
K7 बनाएँ — इसमें 7 बिंदु होंगे और हर बिंदु हर अन्य बिंदु से जुड़ा होगा।
नियम: हर अगले आलेख में एक नया बिंदु जोड़ा जाता है, और यह सभी पूर्व बिंदुओं से जुड़ता है।
रेखाओं की कुल संख्या:
K2 = 1, K3 = 3, K4 = 6, K5 = 10, K6 = 15, त्रिकोणीय संख्या के अनुसार बढ़ती हैं।

3. स्तरीकृत वर्ग (Stacked Squares):
अगला होगा 6×6 वर्ग जिसमें कुल 36 छोटे वर्ग होंगे।
नियम: वर्ग का आकार 1×1, 2×2, 3×3,… क्रमशः बढ़ रहा है।
कुल छोटे वर्गों की संख्या: 1², 2², 3², 4², 5² → वर्ग संख्याएँ

4. स्तरीकृत त्रिभुज (Stacked Triangles):
अगला त्रिभुज होगा 6 पंक्तियों वाला।
नियम: हर त्रिभुज में एक अतिरिक्त पंक्ति जोड़ी जा रही है, और हर पंक्ति में एक बिंदु अधिक होता है।
कुल त्रिभुजों की संख्या: 1, 3, 6, 10, 15 → त्रिकोणीय संख्याएँ

5. कोच चित्रण (Koch Snowflake):
आंशिक रूप से — अगला आकृति बनाना संभव है लेकिन जटिल होगा। क्योंकि हर रेखा को फिर से तीन भागों में बाँटकर उसमें “कोना” जोड़ा जाता है।
नियम: हर चरण में, हर सीधी रेखा को 4 नई रेखाओं से बदला जाता है (एक छोटी पहाड़ी जैसी आकृति)।
कुल रेखाओं की संख्या: 3, 12, 48, 192, … → 3 × 4ⁿ के रूप में बढ़ती है।
1.6 आइए, पता लगाएँ (Page 11, 12)
1. सम बहुभुजों के प्रत्येक आकार अनुक्रम में भुजाओं की संख्या ज्ञात कीजिए। आपको कौन-सा संख्या अनुक्रम प्राप्त होता है? सम बहुभुजों के प्रत्येक आकार अनुक्रम में कटे आकृतियों के कोनों के विषय में आप क्या कहेंगे? क्या आपको वही संख्या अनुक्रम प्राप्त होता है? क्या आप स्पष्ट कर सकते हैं कि ऐसा क्यों होता है?
उत्तर: भुजाओं और कोनों का अनुक्रम:
सम बहुभुजों के प्रत्येक आकार में भुजाओं और कोनों की संख्या 1-1 करके बढ़ती है।
त्रिभुज: 3 भुजाएँ, 3 कोने
चतुर्भुज: 4 भुजाएँ, 4 कोने
पंचभुज: 5 भुजाएँ, 5 कोने
षट्भुज: 6 भुजाएँ, 6 कोने
सप्तभुज: 7 भुजाएँ, 7 कोने
संख्या अनुक्रम:
3, 4, 5, 6, 7…
व्याख्या:
सम बहुभुजों में प्रत्येक कोना एक भुजा से जुड़ा होता है, इसलिए भुजाओं और कोनों की संख्या समान होती है।
2. संपूर्ण आलेखों के प्रत्येक आकार अनुक्रम में रेखाओं की संख्याओं की गणना कीजिए। इससे आपको कौन-सा संख्या अनुक्रम प्राप्त होता है? क्या आप स्पष्ट कर सकते हैं कि ऐसा क्यों होता है?
उत्तर: संपूर्ण आलेख (Complete Graph) वह चित्र होता है जिसमें हर बिंदु (dot/vertex) हर अन्य बिंदु से जुड़ा होता है।
उदाहरण और रेखाओं की संख्या:
| आलेख (Graph) | बिंदुओं की संख्या | रेखाओं की संख्या |
|---|---|---|
| K2 | 2 | 1 |
| K3 | 3 | 3 |
| K4 | 4 | 6 |
| K5 | 5 | 10 |
| K6 | 6 | 15 |
| K7 | 7 | 21 |
आपको जो संख्या अनुक्रम मिलता है:
1, 3, 6, 10, 15, 21, …
यह है: त्रिकोणीय संख्याओं (Triangular Numbers) का अनुक्रम।
स्पष्टीकरण: यदि कोई आलेख (Graph) में n बिंदु हैं, तो हर बिंदु बाकी के (n − 1) बिंदुओं से जुड़ेगा। लेकिन अगर आप सीधे गिनेंगे, तो हर रेखा दो बार गिनी जाएगी (जैसे A से B और B से A एक ही रेखा है)। इसलिए, कुल रेखाओं की संख्या होगी:
\(\frac{n(n−1)}{2}\)उदाहरण: K4 → 4 बिंदु ⇒ \(\frac{4\times 3}{2}\) = 6 रेखाएँ
K6 → 6 बिंदु ⇒ \(\frac{6\times 5}{2}\) = 15 रेखाएँ
3. ढेरित (stacked) वर्गों के अनुक्रम के प्रत्येक आकार में कितने छोटे वर्ग हैं? इससे कौन-सा संख्या अनुक्रम प्राप्त होता है? क्या आप स्पष्ट कर सकते हैं कि ऐसा क्यों होता है?
उत्तर: ढेरित (Stacked) वर्ग का मतलब होता है: ऐसे वर्ग जिनमें छोटे-छोटे वर्ग एक बड़े वर्ग के रूप में एक के ऊपर एक पंक्तियों और स्तंभों में रखे गए होते हैं।
| आकार | छोटे वर्गों की संख्या |
|---|---|
| 1 × 1 | 1 |
| 2 × 2 | 4 |
| 3 × 3 | 9 |
| 4 × 4 | 16 |
| 5 × 5 | 25 |
| 6 × 6 | 36 |
संख्या अनुक्रम है:
1, 4, 9, 16, 25, 36, …
यह कहलाता है: वर्ग संख्याओं (Square Numbers) का अनुक्रम।
स्पष्टीकरण:
जब हम 1 × 1 का वर्ग बनाते हैं — 1 वर्ग
जब हम 2 × 2 का वर्ग बनाते हैं — 2 पंक्तियाँ और 2 स्तंभ = 2 × 2 = 4 छोटे वर्ग
जब हम 3 × 3 बनाते हैं — 3 पंक्तियाँ × 3 स्तंभ = 9 छोटे वर्ग
इसी तरह आगे बढ़ते हैं… इसलिए:
n × n = n²
और हमें मिलती हैं: वर्ग संख्याएँ = 1², 2², 3², 4², …
4. ढेरित त्रिभुजों (Stacked Triangles) के अनुक्रम के प्रत्येक आकार में कितने छोटे त्रिभुज हैं? इससे कौन-सा संख्या अनुक्रम प्राप्त होता है? क्या आप स्पष्ट कर सकते हैं कि ऐसा क्यों होता है? (संकेत – अनुक्रम के प्रत्येक आकार में, प्रत्येक पंक्ति में कितने त्रिभुज हैं?)
उत्तर: ढेरित त्रिभुजों (Stacked Triangles) में छोटे त्रिभुजों की संख्या का अनुक्रम: 1, 4, 9, 16, 25
5. कोच हिमकण (Koch snowflake) वाले अनुक्रम में, एक आकार से अगला आकार प्राप्त करने कि लिए प्रत्येक रेखाखंड ‘-‘ को एक ‘गति उभार (speed bump)’ से प्रतिस्थापित करना पड़ता है। जैसे-जैसे इसे अधिक से अधिक बार किया जाता है, वैसे-वैसे परिवर्तन अत्यधिक छोटे-छोटे रेखाखंडों के साथ छोटे तथा और अधिक छोटे होते जाते हैं। कोच हिमकण के प्रत्येक आकार में कुल कितने रेखाखंड हैं?इनके संगत संख्या अनुक्रम क्या हैं? (3, 12, 48,.अर्थात् 4 की घात का तीन गुना इसका उत्तर हैं, यह अनुक्रम सारणी में नहीं है।)
उत्तर: कोच हिमकण (Koch Snowflake):- यह एक आवृत्त फ्रैक्टल आकृति है जो एक त्रिभुज से शुरू होती है।
हर बार प्रत्येक रेखा को तीन भागों में बाँटा जाता है और बीच के भाग को एक ‘V’ जैसे दो रेखाओं से बदला जाता है — इसे हम “गति उभार (speed bump)” कहते हैं।
| चरण | कुल रेखाखंड | सूत्र |
|---|---|---|
| 0 (शुरुआत) | 3 | मूल त्रिभुज के 3 किनारे |
| 1 | 3 × 4 = 12 | हर रेखा → 4 रेखाएँ |
| 2 | 12 × 4 = 48 | हर रेखा → फिर 4 और |
| 3 | 48 × 4 = 192 | इसी तरह आगे |
| 4 | 192 × 4 = 768 | … |
संख्या अनुक्रम होता है: 3, 12, 48, 192, 768, …
यह है: 3 × 4⁰, 3 × 4¹, 3 × 4², 3 × 4³, 3 × 4⁴, …















I like this answer