Maths Class 7 Symmetry Chapter 12 Exercise 12.2 Question Answer

Solutions For All Chapters Maths Class 7

Ex 12.2 Class 7 Maths Question 1.
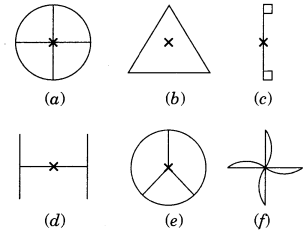
Which of the following figures have rotational symmetry of order more than 1?

Solution:

The figure (a), (b), (d), (e) and (f) have rotational symmetry more than 1.

Question 2.
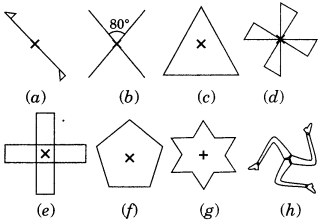
Give the order of rotational symmetry for each figure:

Solution:

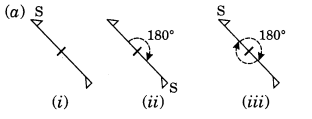
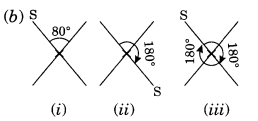
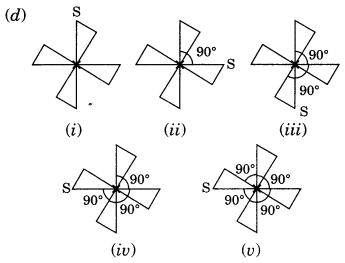
Let us take a point S on one end of the given figure. Rotating by 180°, S comes at other end and then again rotating by 180°, it comes at its original position.
∴ Order of rotational symmetry = 360°/180°=2

Let us take any point S in figure (1). It takes two rotations to come back to its original position.
∴ Order of rotational symmetry = 360°/180° = 2

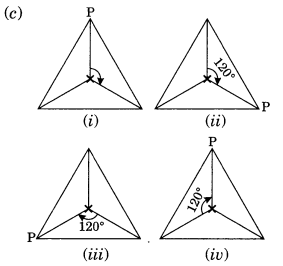
Let us mark any vertex of the given figure. It takes three rotations to come back to its original shape.
∴ Order of rotational symmetry = 360°/120° = 3

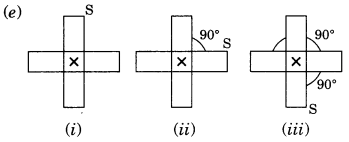
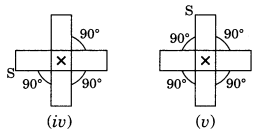
Order of rotational symmetry = 360°/90° = 4

∴ Order of rotational symmetry = 360°/90° = 4
(f) The given figure is a regular pentagon which can take one rotation at an angle of 72°.
∴ Order of rotational symmetry = 360°/72° = 5
(g) The given figure requires six rotations each through an angle of 60°
∴ Order of rotational symmetry = 360°/60 = 6
(h) The given figure requires three rotations, each through an angle of 120°.
∴ Order of rotational symmetry = 360°/120° = 3