Solutions For All Chapters Maths Class 7
Ex 3.3 Class 7 Maths Question 1.
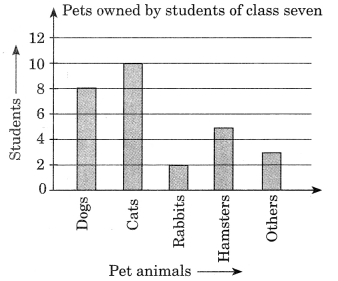
Use the bar graph to answer the following questions.
(a) Which is the most popular pet?
(b) How many students have dog as a pet?
Solution:
From the given bar graph in figure, we have
(a) Cats are the most popular pet among the students.
(b) 8 students have dog as a pet animal.
Ex 3.3 Class 7 Maths Question 2.
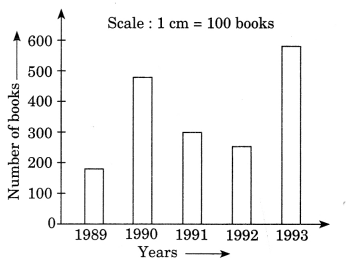
Read the bar graph which shows the number of books sold by a bookstore during five consecutive years and answer the following questions:
(i) About how many books were sold in 1989, 1990, 1992?
(ii) In which year were about 475 books sold? About 225 books sold?
(iii) In which year were fewer than 250 books sold?
(iv) Can you explain how you would estimate the number of books sold in 1989?
Solution:
From the given bar graph, we have
(i) Number of books sold in the year 1989 is about 180, in 1990 is about 490 and in 1992 is about 295.
(ii) About 475 books were sold in 1990. About 225 books were sold in the year 1992.
(iii) Fewer than 250 books were sold in the years 1989 and 1992.
(iv) On y-axis, the line is divided into 10 small parts of 10 books each. So, we can estimate the number of books sold in 1989 is about 180.
Ex 3.3 Class 7 Maths Question 3.
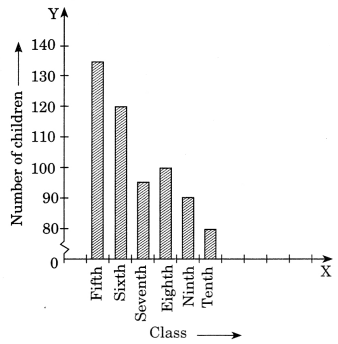
Number of children in six different classes are given below. Represent the data on a bar graph.
| Class | Number of children |
| Fifth | 135 |
| Sixth | 120 |
| Seventh | 95 |
| Eighth | 100 |
| Ninth | 90 |
| Tenth | 80 |
(a) How would you choose a scale?
(b) Answer the following questions:
• Which class has the maximum number of children? And the minimum?
• Find the ratio of students of class sixth to £he students of class eighth.
Solution:
(a) Scale on y-axis is 1 cm = 10 students
(b) • Fifth class has the maximum number of children i.e., 135.
Tenth class has the minimum number of children i.e., 80.
• Number of children in class eight = 100
∴ Ratio of class sixth to the students of class
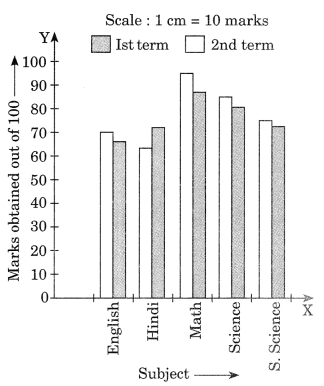
Ex 3.3 Class 7 Maths Question 4.
The performance of a student in 1st term and 2nd term is given. Draw a double bar graph choosing appropriate scale and answer the following:
| Subject | 1st term (M.M. 100) | 2nd term (M.M. 100) |
| English | 67 | 70 |
| Hindi | 72 | 65 |
| Math | 88 | 95 |
| Science | 81 | 85 |
| S. Science | 73 | 75 |
(i) In which subject, has the child improved his performance the most?
(ii) In which subject is the improvement the least?
(iii) Has the performance gone down in any subject?
Solution:
(i) In Math, the performance of the students improved the most.
(ii) In social science, the performance of the students improved the least.
(iii) Yes, in Hindi the performance of the students has gone down.
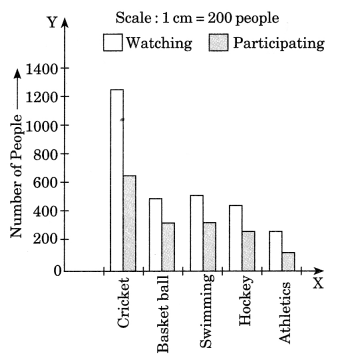
Ex 3.3 Class 7 Maths Question 5.
Consider this data collected from survey of a colony.
| Favourite sport | Watching | Participating |
| Cricket | 1240 | 620 |
| Basket ball | 470 | 320 |
| Swimming | 510 | 320 |
| Hockey | 430 | 250 |
| Athletics | 250 | 105 |
(i) Draw a double bar graph choosing an appropriate scale. What do you infer from the bar graph?
(ii) Which sport is most popular?
(iii) Which is more preferred, watching or participating in sports?
Solution:
(i) The above bar graph depicts the number of people who are watching and who are participating in sports.
(ii) Cricket is the most popular sport.
(iii) Watching the sports is more preferred by the people.
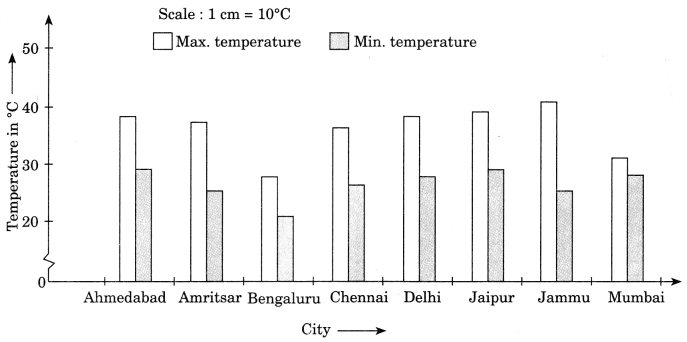
Ex 3.3 Class 7 Maths Question 6.
Take the data giving the minimum and the maximum temperature of various cities given in the beginning of this chapter. Plot a double bar graph using the data and answer the following:
(i) Which city has the largest difference in the minimum and maximum temperature on the given date?
(ii) Which is the hottest city and which is the coldest city?
(iii) Name two cities where maximum temperature of one was less than the minimum temperature of the other.
(iv) Name the city which has the least difference between its minimum and maximum temperature.
| Temperature of cities as on 20.6.2006 | ||
| City | Max. | Min. |
| Ahmedabad | 38°C | 29°C |
| Amritsar | 37°C | 26°C |
| Bengaluru | 28°C | 21°C |
| Chennai | 36°C | 27°C |
| Delhi | 38°C | 28°C |
| Jaipur | 39°C | 29°C |
| Jammu | 41°C | 26°C |
| Mumbai | 32°C | 27°C |
Solution:
Double bar graph:
(i) Jammu has the largest difference between the maximum and minimum temperature i.e. 41°C – 26°C = 15°C
(ii) Hottest city is Jammu with 41°C temperature and coldest city is Bengaluru with 21°C temperature.
(iii) •Bengaluru having its maximum temperature 28°C is less than the minimum temperature 29°C in Ahmedabad.
•Bengaluru having its maximum tem-perature 28°C is less than the maximum temperature 29°C in Jaipur.
(iv) Mumbai has the least difference between its minimum and maximum temperatures i.e. 32°C – 27°C = 5°C
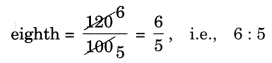

Leave a Reply