Solutions For All Chapters Maths Class 7
Ex 4.2 Class 7 Maths Question 1.
Given first the step you will use to separate the variable and then solve the equation:
(a) x – 1 = 0
(b) x + 1 = 0
(c) x – 1 = 5
(d) x + 6 = 2
(e) y – 4 = -7
(f) y -4 = 4
(g) y + 4 = 4
(h) y + 4 = -4
Solution:
(a) x – 1 = 0
Adding 1 to both sides, we get
x – 1 + l = 0 + 1 ⇒ x = 1
Thus, x = 1 is the required solutions.
Check: Put x = 1 in the given equations
x – 1 = 0
1 – 1 = 0
0 = 0
LHS = RHS
Thus x = 1 is the correct solution.
(b) x + 1 = 0
Subtracting 1 from both sides, we get
x + 1 – 1 = 0 – 1 ⇒ x = -1
Thus x = -1 is the required solution.
Check: Put x = -1 in the given equation
-1 + 1 = 0
0 = 0
LHS = RHS
Thus x = -1 is the correct solution.
(c) x – 1 = 5
Adding 1 to both sides, we get
x – 1 + 1 = 5 + 1 ⇒ x = 6
Thus x = 6 is the required solution.
Check: x – 1 = 5
Putting x = 6 in the given equation
6 – 1 = 5 ⇒ 5 = 5
LHS = RHS
Thus, x = 6 is the correct solution.
(d) x + 6 = 2
Subtracting 6 from both sides, we get
x + 6 – 6 = 2 – 6 ⇒ x = -4
Thus, x = -4 is the required solution.
Check: x + 6 = 2
Putting x = -4, we get
-4 + 6 = 2 ⇒ 2 = 2 LHS = RHS
Thus x = -4 is the correct solution.
(e) y – 4 = -7
Adding 4 to both sides, we get
y – 4 + 4 = -7 + 4 ⇒ y = -3
Thus, y = -3 is the required solution.
Check: y – 4 = -7
Putting y = -3, we get
-3 – 4 = -7 ⇒ -7 = -7
LHS = RHS
Thus, y = -3 is the correct solution.
(f) y – 4 = 4
Adding 4 to both sides, we get
y – 4 + 4 = 4 + 4 ⇒ y = 8
Thus, y = 8 is the required solution.
Check: y – 4 = 4
Putting y = 8, we get
8 – 4 = 4 ⇒ 4 = 4
LHS = RHS
Thus y = 8 is the correct solution.
(g) y + 4 = 4
Subtracting 4 from both sides, we get
y + 4 – 4 = 4 – 4 ⇒ y = 0
Thus y = 0 is the required solution.
Check: y + 4 = 4
Putting y = 0, we get
0 + 4 = 4 ⇒ 4 = 4
LHS = RHS
Thus y = 0 is the correct solution.
(h) y + 4 =-4
Subtracting 4 from both sides, we get
y + 4 – 4 = -4 – 4 ⇒ y = -8
Thus, y = -8 is the required solution.
Check: y + 4 = -4
Putting y = -8, we get
-8 + 4 = -4 ⇒ -4 = -4
LHS = RHS
Thus, y = -8 is the correct solution.
Ex 4.2 Class 7 Maths Question 2.
Give first the step you will use to separate the variable and then solve the following equation:
Solution:
Ex 4.2 Class 7 Maths Question 3.
Give the steps you will use to separate the variables and then solve the equation:
(a) 3n – 2 = 46
(b) 5m + 7 = 17
c) 20 p/3 = 40
(d)3 p/10 = 6
Solution:
(a) 3n – 2 = 46
⇒ 3n- 2 + 2 = 46+ 2 (adding 2 to both sides)
⇒ 3n = 48
⇒ 3n + 3 = 48 ÷ 3
(b) 5m + 7 = 17
⇒ 5m+ 7 – 7 = 17 – 7 (Subtracting 7 from both sides)
⇒ 5m = 10
⇒ 5m + 5 = 10 ÷ 5 (Dividing both sides by 5)
(c) 20 p/3 = 40
(d) 3 p/10 = 6
⇒3 p/10 × 10=6 × 10 (Multiplying both sides by 10)
⇒ 3p = 60
⇒ 3p ÷ 3 = 60 ÷ 3 (Dividing both sides by 3)
Ex 4.2 Class 7 Maths Question 4.
Solve the following equations:
(a) 10p = 100
(b) 10p + 10 = 100
(c) p/4 = 5
(d)-p/3 = 5
(e) 3 p/4 = 6
(f) 3s = -9
(g) 3s + 12 = 0
(h) 3s = 0
(i) 2q = 6
(j) 2q – 6 = 0
(k) 2q + 6 = 0
(l) 2q + 6 = 12
Solution:
a) 10p = 100
⇒ 10p ÷ 10 = 100 ÷ 10 (Dividing both sides by 10)
⇒ 10p ÷ 10 = 100 ÷ 10 (Dividing both sides by 10)
p = 100/10 = 10
Thus p = 10
(b) 10p + 10 = 100
⇒ 10p + 10 – 10 = 100 -10 (Subtracting 10 from both sides)
⇒ 10p = 90
⇒ 10p ÷ 10 = 90 ÷ 10 (Dividing both side by 10)
p = 90/10 = 9
Thus p = 9
(l) 2q + 6 = 12
⇒ 2q + 6 – 6 = 12 – 6 ( Subtracting 6 from both sides)
⇒ 2q = 6
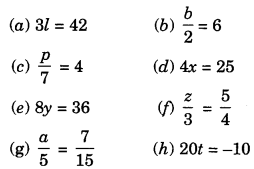
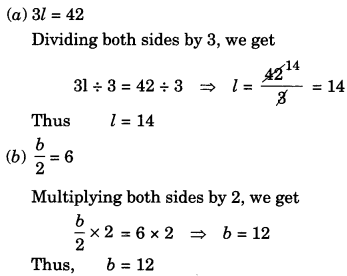
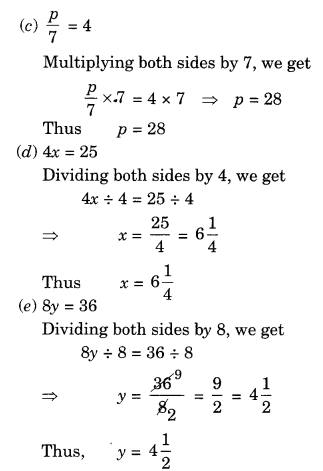
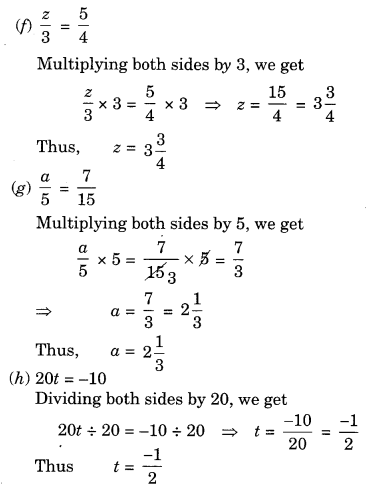
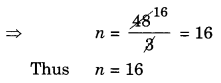
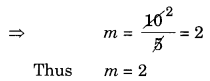
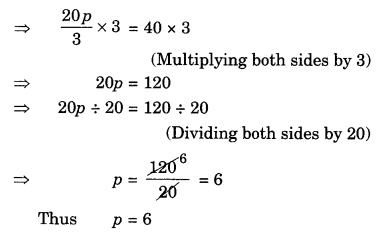
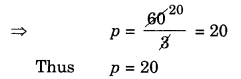


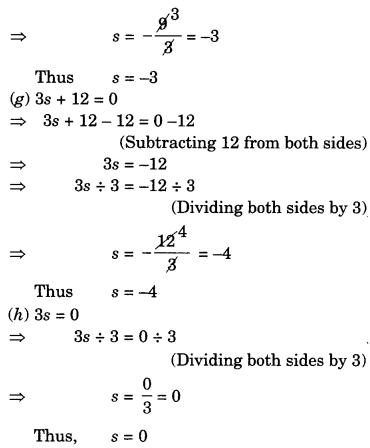
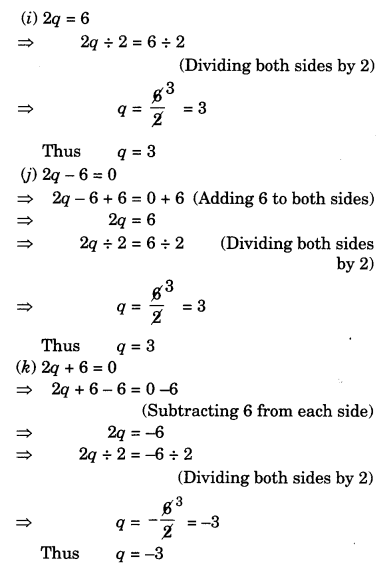
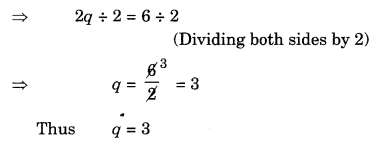

Leave a Reply