Maths Class 7 Triangle & its Properties Chapter 6 Exercise 6.3 Question Answer

Solutions For All Chapters Maths Class 7

Ex 6.3 Class 7 Maths Question 1.
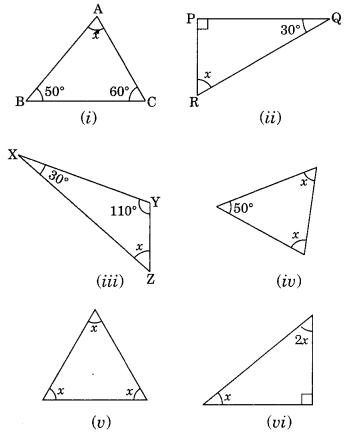
Find the value of the unknown x in the following diagrams:

Solution:

(i) By angle sum property of a triangle, we have
∠x + 50° + 60° = 180°
⇒ ∠x + 110° = 180°
∴ ∠x = 180° – 110° = 70°

(ii) By angle sum property of a triangle, we have
∠x + 90° + 30 = 180° [∆ is right angled triangle]
⇒ ∠x + 120° = 180°
∴ ∠x – 180° – 120° = 60°

(iii) By angle sum property of a triangle, we have
∠x + 30° + 110° – 180°
⇒ ∠x + 140° = 180°
∴ ∠x = 180° – 140° = 40°

(iv ) By angle sum property of a triangle, we have
∠x + ∠x + 50° = 180°
⇒ 2x + 50° = 180°
⇒ 2x = 180° – 50°
⇒ 2x = 130°
∴ x = 130°/2 = 65°

(v) By angle sum property of a triangle, we have
∠x + ∠x +∠x =180°
⇒ 3 ∠x = 180°
∴ ∠x = 180°/3 = 60°

(vi) By angle sum property of a triangle, we have
x + 2 x + 90° = 180° (∆ is right angled triangle)
⇒ 3x + 90° = 180°
⇒ 3x = 180° – 90°
⇒ 3x = 90°
∴ x = 90°/3 = 30°

Ex 6.3 Class 7 Maths Question 2.
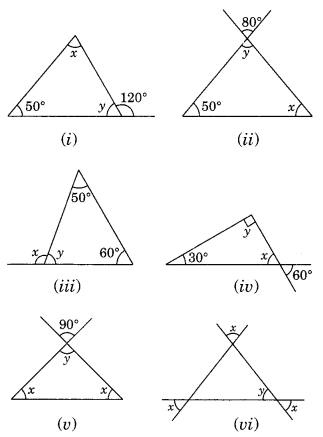
Find the values of the unknowns x and y in the following diagrams:

Solution:

(i) ∠x + 50° = 120° (Exterior angle of a triangle)
∴ ∠x = 120°- 50° = 70°
∠x + ∠y + 50° = 180° (Angle sum property of a triangle)
70° + ∠y + 50° = 180°
∠y + 120° = 180°
∠y = 180° – 120°
∴ ∠y = 60°
Thus ∠x = 70 and ∠y – 60°

(ii) ∠y = 80° (Vertically opposite angles are same)
∠x + ∠y + 50° = 180° (Angle sum property of a triangle)
⇒ ∠x + 80° + 50° = 180°
⇒ ∠x + 130° = 180°
∴ ∠x = 180° – 130° = 50°
Thus, ∠x = 50° and ∠y = 80°

(iii) ∠y + 50° + 60° = 180° (Angle sum property of a triangle)
∠y + 110° = 180°
∴ ∠y = 180°- 110° = 70°
∠x + ∠y = 180° (Linear pairs)
⇒ ∠x + 70° = 180°
∴ ∠x = 180° – 70° = 110°
Thus, ∠x = 110° and y = 70°

(iv) ∠x = 60° (Vertically opposite angles)
∠x + ∠y + 30° = 180° (Angle sum property of a triangle)
⇒ 60° + ∠y + 30° = 180°
⇒ ∠y + 90° = 180°
⇒ ∠y = 180° – 90° = 90°
Thus, ∠x = 60° and ∠y = 90°

(v) ∠y = 90° (Vertically opposite angles)
∠x + ∠x + ∠y = 180° (Angle sum property of a triangle)
⇒ 2 ∠x + 90° = 180°
⇒ 2∠x = 180° – 90°
⇒ 2∠x = 90°
∴ ∠x = 90°/2 = 45°
Thus, ∠x = 45° and ∠y = 90°

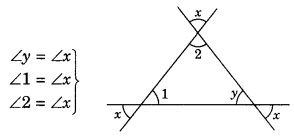
(vi) From the given figure, we have

Adding both sides, we have
∠y + ∠1 + ∠2 = 3∠x
⇒ 180° = 3∠x (Angle sum property of a triangle)
∴ ∠x = 180°/3 = 60°
∠x = 60°, ∠y = 60°