Solutions For All Chapters Maths Class 7
Ex 6.4 Class 7 Maths Question 1.
Is it possible to have a triangle with the following sides?
(i) 2 cm, 3 cm, 5 cm
(ii) 3 cm, 6 cm, 7 cm
(iii) 6 cm, 3 cm, 2 cm
Solution:
We know that for a triangle, the sum of any two sides must be greater than the third side.
(i) Given sides are 2 cm, 3 cm, 5 cm
Sum of the two sides = 2 cm + 3 cm = 5 cm Third side = 5 cm
We have, Sum of any two sides = the third side i.e. 5 cm = 5 cm
Hence, the triangle is not possible.
(ii) Given sides are 3 cm, 6 cm, 7 cm
Sum of the two sides = 3 cm + 6 cm = 9 cm Third side = 7 cm
We have sum of any two sides > the third
side. i.e. 9 cm > 7 cm
Hence, the triangle is possible.
(iii) Given sides are 6 cm, 3 cm, 2 cm
Sum of the two sides = 3 cm + 2 cm – 5 cm Third side = 6 cm
We have, sum of any two sides < the third sid6 i.e. 5 cm < 6 cm Hence, the triangle is not possible.
Ex 6.4 Class 7 Maths Question 2.
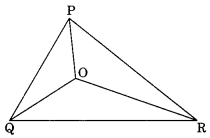
Take any point O in the interior of a triangle PQR . Is
(i) OP + OQ > PQ?
(ii) OQ + OR > QR?
(iii) OR + OP > RP?
Solution:
(i) Yes, In ∆OPQ, we have
OP + OQ > PQ
[Sum of any two sides of a triangle is greater than the third side]
(ii) Yes, In ∆OQR, we have OQ + OR > QR
[Sum of any two sides of a triangle is greater than the third side]
(iii) Yes, In ∆OPR, we have OR + OP > RP
[Sum of any two sides of a triangle is greater than the third side]
Ex 6.4 Class 7 Maths Question 3.
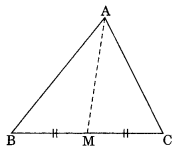
AM is a median of a triangle ABC.
Is AB + BC + CA > 2AM ?
(Consider the sides of triangles ∆ABM and ∆AMC)
Solution:
Yes, In AABM, we have
AB + BM > AM …(i)
[Sum of any two sides of a triangle is greater than the third side]
In ∆AMC, we have
AC + CM > AM …(ii)
[Sum of any two sides of a triangle is greater than the third side]
Adding eq (i) and (ii), we have
AB + AC + BM + CM > 2AM
AB + AC + BC + > 2AM
AB + BC + CA > 2AM
Hence, proved.
Ex 6.4 Class 7 Maths Question 4.
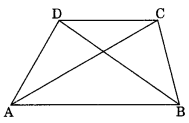
ABCD is a quadrilateral.
Is AB + BC + CD + DA > AC + BD?
Solution:
Yes, Given \squareABCD in which AC and BD are its diagonals.
In ∆ABC, we have
AB + BC > AC …(i)
[Sum of any two sides is greater than the third side]
In ∆BDC, we have
BC + CD > BD …(ii)
[Sum of any two sides is greater than the third side]
In ∆ADC, we have
CD + DA > AC …(iii)
[Sum of any two sides is greater than the third side]
In ∆DAB, we have
DA + AB > BD …(iv)
[Sum of any two sides is greater than the third side]
Adding eq. (i), (ii), (iii) and (iv), we get
2AB + 2BC + 2CD + 2DA > 2AC + 2BD or AB + BC + CD + DA > AC + BD [Dividing both sides by 2]
Hence, proved.
Ex 6.4 Class 7 Maths Question 5.
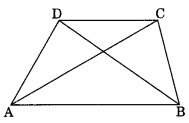
ABCD is a quadrilateral.
Is AB + BC + CD + DA < 2(AC + BD)?
Solution:
Yes, we have a quadrilateral ABCD.
In ∆AOB, we have AB < AO + BO …(i)
[Any side of a triangle is less than the sum of other two sides]
In ∆BOC, we have
BC < BO + CO …(ii)
[Any side of a quadrilateral is less than the sum of other two sides]
In ∆COD, we have
CD < CO + DO …(iii)
[Any side of a triangle is less than the sum of other two sides]
In ∆AOD, we have
DA < DO + AO …(iv)
[Any side of a triangle is less than the sum of other two sides]
Adding eq. (i), (ii), (iii) and (iv), we have
AB + BC + CD + DA
∠2AO + ∠BO + ∠CO + ∠DO
∠2(AO + BO + CO + DO)
∠2 [(AO + CO) + (BO + DO)]
∠2(AC + BD)
Thus, AB + BC + CD + DA < 2(AC + BD)
Hence, proved.
Ex 6.4 Class 7 Maths Question 6.
The length of two sides of a triangle are 12 cm and 15 cm. Between what two measures should the length of the third side fall?
Solution:
Sum of two sides
= 12 cm + 15 cm = 27 cm
Difference of the two sides
= 15 cm – 12 cm = 3 cm
∴ The measure of third side should fall between 3 cm and 27 cm.
Leave a Reply