Question Answer For All Chapters – Ganita Prakash Class 7th
Page 46-47
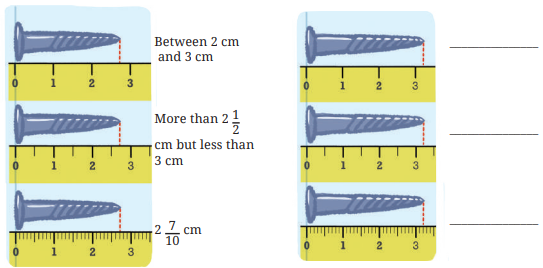
In the following figure, screws are placed above a scale. Measure them and write their length in the space provided.
Ans:
(Q.) Which scale helped you measure the length of the screws accurately? Why?
Ans: “The third scale helped us measure the length of the screws accurately because each centimeter is divided into 10 equal parts (millimetres).”
(Q.) Can you explain why the unit was divided into smaller parts to measure the screws?
Ans: “The unit was divided into smaller parts to measure the screws because the difference in their lengths was very small, and smaller units help in measuring such tiny differences accurately.”
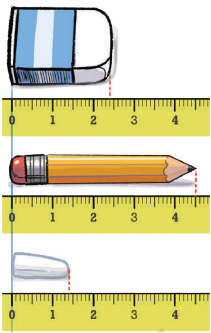
(Q.) Measure the following objects using a scale and write their measurements in centimeters (as shown earlier for the lengths of the screws): pen, sharpener, and any other object of your choice.
Ans:“Students do this themselves.”
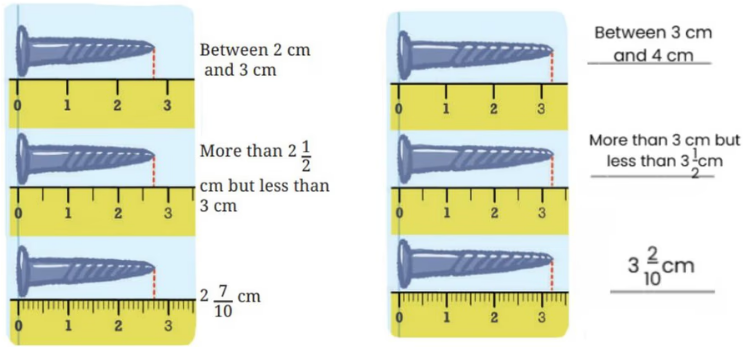
(Q.) Write the measurements of the objects shown in the picture:
Ans:
Eraser = 2\(\frac{4}{10}\)cm (2.4 cm)
Pencil = 4\(\frac{5}{10}\)cm (4.5 cm)
Chalk = 1\(\frac{4}{10}\)cm (1.4 cm)
3.2 A Tenth Part (Pages 49-52)
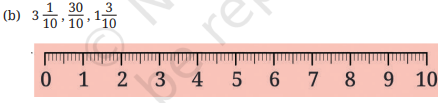
(Q.) Arrange these lengths in increasing order:
(a.) \(\frac{9}{10}\)
(b.) 1\(\frac{7}{10}\)
(c.) \(\frac{130}{10}\)
(d.) 13\(\frac{1}{10}\)
(e.) 10\(\frac{5}{10}\)
(f.) 7\(\frac{6}{10}\)
(g.) 6\(\frac{7}{10}\)
(h.) \(\frac{4}{10}\)
Ans:
(a.) \(\frac{9}{10}\) = \(\frac{9}{10}\)
(b.) 1\(\frac{7}{10}\) = \(\frac{17}{10}\)
(c.) \(\frac{130}{10}\) = \(\frac{130}{10}\)
(d.) 13\(\frac{1}{10}\) = \(\frac{131}{10}\)
(e.) 10\(\frac{5}{10}\) = \(\frac{105}{10}\)
(f.) 7\(\frac{6}{10}\) = \(\frac{76}{10}\)
(g.) 6\(\frac{7}{10}\)= \(\frac{67}{10}\)
(h.) \(\frac{4}{10}\) = \(\frac{4}{10}\)
Now, arrange in increasing order:
(h.) \(\frac{4}{10}\) (a.)\(\frac{9}{10}\) (b.) \(\frac{17}{10}\) (g.)\(\frac{67}{10}\) (f.)\(\frac{76}{10}\) (e.) \(\frac{105}{10}\) (c.)\(\frac{130}{10}\) (d.)\(\frac{131}{10}\)
(Q.) Arrange the following lengths in increasing order: 4\(\frac{1}{10}\), \(\frac{4}{10}\), \(\frac{41}{10}\), 41\(\frac{1}{10}\)
Ans: 4\(\frac{1}{10}\) = \(\frac{41}{10}\)
\(\frac{4}{10}\) = \(\frac{4}{10}\)
\(\frac{41}{10}\) = \(\frac{41}{10}\)
41\(\frac{1}{10}\) = \(\frac{411}{10}\)
\(\frac{4}{10}\)<\(\frac{41}{10}\)=\(\frac{41}{10}\)<\(\frac{411}{10}\)
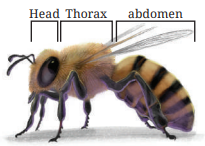
(Q.) The lengths of the body parts of a honeybee are given. Find its total length.
Head: 2\(\frac{3}{10}\) units
Thorax: 5\(\frac{4}{10}\) units
Abdomen: 7\(\frac{5}{10}\) units
Ans: 2\(\frac{3}{10}\) units + 5\(\frac{4}{10}\) units + 7\(\frac{5}{10}\) units
(2+5+7) + (\(\frac{3}{10}\)+\(\frac{4}{10}\)+\(\frac{5}{10}\)) units
= 14 + \(\frac{12}{10}\) units = 14 + \(\frac{10+2}{10}\) units
= 14 + \(\frac{10}{10}\) + \(\frac{2}{10}\) units
= 14 + 1 + \(\frac{2}{10}\) = 15 + \(\frac{2}{10}\)
= 15\(\frac{2}{10}\)units
(Q.) A Celestial Pearl Danio’s length is 2\(\frac{4}{10}\)cm, and the length of a Philippine Goby is \(\frac{9}{10}\)cm. What is the difference in their lengths?
Ans: A Celestial Pearl Danio’s length is = 2\(\frac{4}{10}\)cm = \(\frac{24}{10}\)cm
The length of a Philippine Goby is = \(\frac{9}{10}\)cm
So, the difference in their lengths =
= \(\frac{24}{10}\)cm – \(\frac{9}{10}\)cm
= \(\frac{15}{10}\)cm = 1\(\frac{5}{10}\)cm
(Q.) How big are these fish compared to your finger?
Ans: Students do this themselves.
(Q.) Observe the given sequences of numbers. Identify the change after each term and extend the pattern:
Ans:
(a)
(b)
(c)
(d)
(e)
(f)
3.3 A Hundredth Part (Pages 54-56)
Observe the figure below. Notice the markings and the corresponding lengths written in the boxes when measured from 0. Fill the lengths in the empty boxes.
Ans:
First Box
This marking lies between 0 and 1, slightly past 0.5.
Length = \(\frac{5}{10}\) + \(\frac{5}{100}\)
= \(\frac{50}{100}\) + \(\frac{5}{100}\)
= \(\frac{55}{100}\)
Second Box
This one lies just after 1 by 0.55 units.
Length = 1 + \(\frac{5}{10}\) + \(\frac{5}{100}\)
= \(\frac{100}{100}\) + \(\frac{50}{100}\) + \(\frac{5}{100}\)
= \(\frac{155}{100}\)
Third Box
This marking is a bit further after 1, around 1.74.
Length = 1 + \(\frac{7}{10}\) + \(\frac{4}{100}\)
= \(\frac{100}{100}\) + \(\frac{70}{100}\) + \(\frac{4}{100}\)
= \(\frac{174}{100}\)
Fourth Box
Length = 2 + \(\frac{2}{100}\)
= \(\frac{200}{100}\) + \(\frac{2}{100}\)
= \(\frac{202}{100}\)
Fifth Box
Length = 2 + \(\frac{4}{10}\)
\(\frac{200}{100}\) + \(\frac{40}{100}\)
= \(\frac{240}{100}\)
For the lengths shown below write the measurements and read out the measures in words.
Ans:
Ans:
Ans:
Ans:
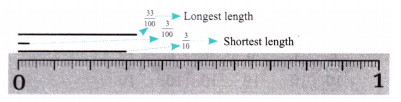
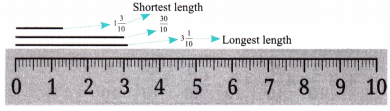
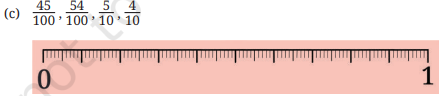
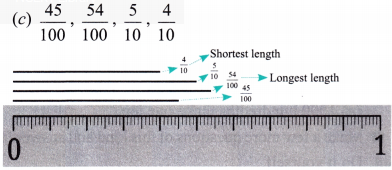
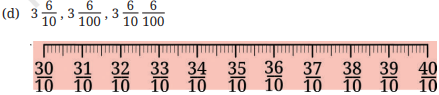
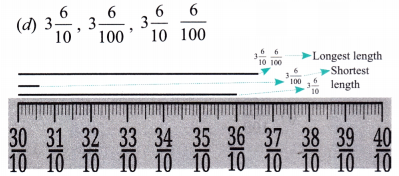
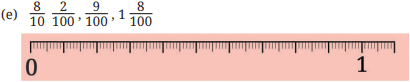
In each group, identify the longest and the shortest lengths. Mark each length on the scale.
Ans:
Ans:
Ans:
Ans:
Ans:
Ans:
Figure it Out (Page 58)
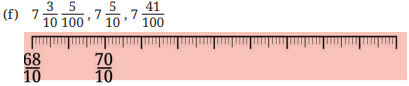
Find the sums and differences:
(a) \(\frac{3}{10}\) + 3\(\frac{4}{100}\)
(b) 9\(\frac{5}{10}\) \(\frac{7}{100}\)+ 2\(\frac{1}{10}\) \(\frac{3}{100}\)
(c) 15\(\frac{6}{10}\) \(\frac{4}{100}\)+ 14\(\frac{3}{10}\) \(\frac{6}{100}\)
(d) 7\(\frac{7}{100}\) – 4\(\frac{4}{100}\)
(e) 8\(\frac{6}{100}\) – 5\(\frac{3}{100}\)
(f) 12\(\frac{6}{100}\) \(\frac{2}{100}\) – \(\frac{9}{10}\) \(\frac{9}{100}\)
Ans: (a) \(\frac{3}{10}\) + 3\(\frac{4}{100}\)
\(\frac{3}{10}\) + 3 + \(\frac{4}{100}\)
3 + \(\frac{3}{10}\)+\(\frac{4}{100}\) = 3\(\frac{3}{10}\) \(\frac{4}{100}\)
= 3\(\frac{34}{100}\)
(d)
Page No – 61
We can ask similar questions about fractional parts:
(a) How many thousandths make one unit?
(b) How many thousandths make one tenth?
(c) How many thousandths make one hundredth?
(d) How many tenths make one ten?
(e) How many hundredths make one ten?
Ans:
(a) 1000 thousandths make one unit.
(b) 100 thousandths make one tenth.
(c) 10 thousandths make one hundredth.
(d) 100 tenths make one ten.
(e) 1000 hundredths make one ten.
Page No – 63, 64
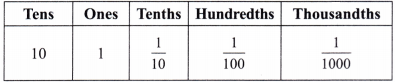
Make a place value table similar to the one above. Write each quantity in decimal form and in terms of place value, and read the number:
(a) 2 ones, 3 tenths and 5 hundredths
(b) 1 ten and 5 tenths
(c) 4 ones and 6 hundredths
(d) 1 hundred, 1 one and 1 hundredth
(e) \(\frac{8}{100}\) and \(\frac{9}{10}\)
(f) \(\frac{5}{100}\)
(g) \(\frac{1}{10}\)
(h) 2\(\frac{1}{100}\), 4\(\frac{1}{10}\), 7\(\frac{7}{1000}\)
| No. | Quantity Description | Decimal Form | In Terms of Place Value | Number in Words |
|---|---|---|---|---|
| (a) | 2 ones, 3 tenths, 5 hundredths | 2.35 | (2 × 1) + (3 × 1/10) + (5 × 1/100) | Two point three five |
| (b) | 1 ten, 5 tenths | 10.5 | (1 × 10) + (5 × 1/10) | Ten point five |
| (c) | 4 ones, 6 hundredths | 4.06 | (4 × 1) + (6 × 1/100) | Four point zero six |
| (d) | 1 hundred, 1 one, 1 hundredth | 101.01 | (1 × 100) + (1 × 1) + (1 × 1/100) | One hundred one point zero one |
| (e) | 9 tenths and 8 hundredths | 0.98 | (9 × 1/10) + (8 × 1/100) | Zero point nine eight |
| (f) | 5 hundredths | 0.05 | (5 × 1/100) | Zero point zero five |
| (g) | 1 tenth | 0.1 | (1 × 1/10) | Zero point one |
| (h) | 6 ones, 4 tenths, 7 hundredths, 7 thousandths | 6.477 | (6 × 1) + (4 × 1/10) + (7 × 1/100) + (7 × 1/1000) | Six point four seven seven |
Q. Write these quantities in decimal form: (a) 234 hundredths, (b) 105 tenths.
Ans: (a) 234 hundredths
We know: 1 hundredth = \(\frac{1}{100}\)
So,
234 hundredths = \(\frac{234}{100}\)
= \(\frac{200+30+4}{100}\)
= \(\frac{200}{100}\) + \(\frac{30}{100}\) + \(\frac{4}{100}\)
= 2+\(\frac{3}{10}\) + \(\frac{4}{100}\)
= 2 ones + 3 tenths + 4 hundredths
= 2.34
(b) 105 tenths = \(\frac{105}{10}\)
= \(\frac{100+5}{10}\)
= \(\frac{100}{10}\) + \(\frac{5}{10}\)
= 10 + \(\frac{5}{10}\)
= 1 ten + 5 tenth
= 1.5
3.5 Units of Measurement (Page No – 65,66)
Q. Fill in the blanks below (mm <–> cm)
Ans:
- 1 cm = 10 mm
- 1 mm = 0.1 cm
| 12 mm = 1.2 cm | 56 mm = 5.6 cm | 70 mm = 7.0 cm |
| 9 mm = 0.9 cm | 134 mm = 13.4 cm | 2036 mm = 203.6 cm |
Q. Fill in the blanks below (cm <–> m):
Ans:
- 1 m = 100 cm
- 1 cm = 0.01 m
| 36 cm = 0.36 m | 50 cm = 0.5 m | 89 cm = 0.89 m |
| 4 cm = 0.04 m | 325 cm = 3.25 m | 207 cm = 2.07 m |
Q. How many mm does 1 meter have?
Ans: 1000 mm = 1 m
Page No – 67,68
Q. Fill in the blanks below (g <–> kg)
Ans:
- 1 kg = 1000 g
- 1 g = 0.001 kg
| 465 g = 0.465 kg | 68 g = 0.068 kg | 1560 g = 1.56 kg |
| 704 g = 0.704 kg | 560 g = 0.56 kg | 2500 g = 2.5 kg |
Page No – 69
Q. Fill in the blanks below (rupee <–> paise)
Ans:
- 1 Rupee = 100 Paise
- 1 Paise = 0.01 Rupee
| 10 p = ₹ 0.1 | 5p = ₹ 0.05 | 36 p = ₹ 0.36 |
| 50 p = ₹ 0.50 | 99 p = ₹ 0.99 | 250 p = ₹2.50 |
(a.)
(b.)
(c.)
(d.)
(e.)
(f.)
3.6 Locating and Comparing Decimals (Page No – 69)
Q. Name all the divisions between 1 and 1.1 on the number line.
Ans: The divisions between 1 and 1.1 represent the decimal numbers 1.01, 1.02, 1.03, 1.04, 1.05, 1.06, 1.07, 1.08, and 1.09 on the number line.
Q. Identify and write the decimal numbers against the letters.
Ans:“The letters on the number line show various decimal numbers.”
A → 5.09, B → 5.13, C → 5.2, D → 5.31
Page No – 71 – 73
0.9, 1.1, 1.01, and 1.11
Q. Which of the above is closest to 1.09?
Ans: Let’s compare each number’s distance from 1.09:
1.09 – 0.9 = 0.19
1.09 – 1.1 = 0.01
1.09 – 1.01 = 0.08
1.09 – 1.11 = 0.02
The smallest difference is 0.01, for 1.1.
Therefore, 1.1 is closest to 1.09.
Q. Which among these is closest to 4: 3.56, 3.65, 3.099?
Ans: Let’s find how far each number is from 4:
4 − 3.56 = 0.44
4 − 3.65 = 0.35
4 − 3.099 = 0.901
The smallest difference is 0.35, for 3.65.
Therefore, 3.65 is closest to 4.
Q. Which among these is closest to 1: 0.8, 0.69, 1.08?
Ans: Let’s check the distance of each number from 1:
- 1 − 0.8 = 0.2
- 1 − 0.69 = 0.31
- 1 − 1.08 = 0.08
The smallest difference is 0.08, for 1.08.
Therefore, 1.08 is closest to 1.
Q. In each case below use the digits 4, 1, 8, 2, and 5 exactly once and try to make a decimal number as close as possible to 25.
Ans: We must use the digits 4, 1, 8, 2, and 5 exactly once to make a decimal number as close as possible to 25.
Let’s test possible combinations:
- 24.815 → difference = 25 − 24.815 = 0.185
- 25.184 → difference = 25.184 − 25 = 0.184
- 25.418 → difference = 0.418
- 24.852 → difference = 0.148 (smaller difference)
- 25.148 → difference = 0.148 (equally close)
The decimal numbers 24.852 or 25.148 are the closest to 25 using the digits 4, 1, 8, 2, and 5 once each.
3.7 Addition and Subtraction of Decimals (Page No – 74)
Q. Write the detailed place value computation for 84.691 – 77.345, and its compact form.
Ans: 84.691−77.345
Break into place values:
(80+4+0.6+0.09+0.001)−(70+7+0.3+0.04+0.005)
| Place Value | Calculation | Result |
|---|---|---|
| Tens | 80 − 70 | 10 |
| Ones | 4 − 7 (borrow 1 ten → 14 − 7 = 7), tens become 9 | 7 |
| Tenths | 0.6 − 0.3 | 0.3 |
| Hundredths | 0.09 − 0.04 | 0.05 |
| Thousandths | 0.001 − 0.005 (borrow → 0.011 − 0.005) | 0.006 |
Add up:
7+0.3+0.05+0.006 = 7.356
Figure it Out (Page No – 75)
1. Find the sums
(a) 5.3 + 2.6
(b) 18 + 8.8
(c) 2.15 + 5.26
(d) 9.01 + 9.10
(e) 29.19 + 9.91
(f) 0.934 + 0.6
(g) 0.75 + 0.03
(h) 6.236 + 0.487
Ans:
(a) 5.3 + 2.6 = 7.9
(b) 18 + 8.8 = 26.8
(c) 2.15 + 5.26 = 7.41
(d) 9.01 + 9.10 = 18.11
(e) 29.19 + 9.91 = 39.10
(f) 0.934 + 0.6 = 1.534
(g) 0.75 + 0.03 = 0.78
(h) 6.236 + 0.487 = 6.723
2. Find the differences
(a) 5.6 – 2.3
(b) 18 – 8.8
(c) 10.4 – 4.5
(d) 17 – 16.198
(e) 17 – 0.05
(f) 34.505 – 18.1
(g) 9.9 – 9.09
(h) 6.236 – 0.487
Ans:
(a) 5.6 − 2.3 = 3.3
(b) 18 − 8.8 = 9.2
(c) 10.4 − 4.5 = 5.9
(d) 17 − 16.198 = 0.802
(e) 17 − 0.05 = 16.95
(f) 34.505 − 18.1 = 16.405
(g) 9.9 − 9.09 = 0.81
(h) 6.236 − 0.487 = 5.749
Figure it Out (Page No – 75)
Observe this sequence of decimal numbers and identify the change after each term.
4.4, 4.8. 5.2, 5.6, 6.0,….
We can see that 0.4 is being added to a term to get the next term.
Q. Continue this sequence and write the next 3 terms.
Ans: 4.4, 4.8. 5.2, 5.6, 6.0, 6.4, 6.8, 7.2
Q. Similarly, identify the change and write the next 3 terms for each sequence given below. Try to do this computation mentally.
(a) 4.4, 4.45, 4.5, … (b) 25.75, 26.25, 26.75, …
(c) 10.56, 10.67, 10.78, … (d) 13.5, 16, 18.5, …
(e) 8.5, 9.4, 10.3, … (f) 5, 4.95, 4.90, …
(g) 12.45, 11.95, 11.45, … (h) 36.5, 33, 29.5, …
Ans:
(a) 4.4, 4.45, 4.5
→ Difference = +0.05
Next 3 terms: 4.55, 4.6, 4.65
(b) 25.75, 26.25, 26.75
→ Difference = +0.5
Next 3 terms: 27.25, 27.75, 28.25
(c) 10.56, 10.67, 10.78
→ Difference = +0.11
Next 3 terms: 10.89, 11.00, 11.11
(d) 13.5, 16, 18.5
→ Difference = +2.5
Next 3 terms: 21.0, 23.5, 26.0
(e) 8.5, 9.4, 10.3
→ Difference = +0.9
Next 3 terms: 11.2, 12.1, 13.0
(f) 5, 4.95, 4.90
→ Difference = –0.05
Next 3 terms: 4.85, 4.80, 4.75
(g) 12.45, 11.95, 11.45
→ Difference = –0.5
Next 3 terms: 10.95, 10.45, 9.95
(h) 36.5, 33, 29.5
→ Difference = –3.5
Next 3 terms: 26.0, 22.5, 19.0
Estimating Sums and Differences (Pages 76)
Sonu has observed sums and differences of decimal numbers and says, “If we add two decimal numbers, then the sum will always be greater than the sum of their whole number parts. Also, the sum will always be less than 2 more than the sum of their whole number parts.”
Let us use an example to understand what his claim means: If the two numbers to be added are 25.936 and 8.202, the claim is that their sum will be greater than 25 + 8 (whole number parts) and will be less than 25 + 1 + 8 + 1.
Q. What do you think about this claim? Verify if this is true for these numbers. Will it work for any 2 decimal numbers?
Ans: The given numbers are 25.936 and 8.202.
The sum of their whole number parts is 25 + 8 = 33.
The actual sum of the two decimal numbers is 25.936 + 8.202 = 34.138.
We can see that 33 < 34.138 < (33 + 2).
Now, take another example — 1.532 and 4.536.
The sum of their whole number parts is 1 + 4 = 5.
Their total sum is 1.532 + 4.536 = 6.068.
Here also, 5 < 6.068 < (5 + 2).
Therefore, Sonu’s claim is correct —
The sum of any two decimal numbers is always greater than the sum of their whole number parts and less than 2 more than that sum.
Q. What about for the sum of 25.93603259 and 8.202?
Ans: The given numbers are 25.93603259 and 8.202.
The sum of their whole number parts is 25 + 8 = 33, and the sum of the two decimal numbers is 25.93603259 + 8.202 = 34.13803259.
Clearly, 33 < 34.13803259 < (33 + 2).
Q. Similarly, come up with a way to narrow down the range of whole numbers within which the difference of two decimal numbers will lie.
Ans: When we subtract two decimal numbers, the result will always lie between two whole numbers — just like in addition.
If we take two decimal numbers, say A.B and C.D (where A and C are whole parts and B, D are decimal parts), then their difference will always be a little less than the difference of their whole number parts plus 1, and greater than or equal to the difference of their whole number parts minus 1.
So, the difference will lie between (difference of whole parts – 1) and (difference of whole parts + 1).
Example:
For 25.936 – 8.202,
Difference of whole number parts = 25 – 8 = 17.
Actual difference = 17.734.
Clearly, (17 – 1) < 17.734 < (17 + 1) → 16 < 17.734 < 18.
Thus, the difference of two decimal numbers will always lie within one less and one more than the difference of their whole number parts.
Figure it Out (Pages 78-80)
1. Convert the following fractions into decimals:
(a) \(\frac{5}{100}\)
(b) \(\frac{16}{1000}\)
(c) \(\frac{12}{10}\)
(d) \(\frac{254}{1000}\)
Ans:
2. Convert the following decimals into a sum of tenths, hundredths and thousandths:
(a) 0.34 (b) 1.02 (c) 0.8 (d) 0.362
Ans:
(a) 0.34
→ The first digit after the decimal (3) is in the tenths place.
→ The second digit (4) is in the hundredths place.
So,
0.34 = 3 tenths + 4 hundredths
= (3 × \(\frac{1}{10}\)) + (4 × \(\frac{1}{100}\))
\(\frac{3}{10}\) + \(\frac{4}{100}\)
(b) 1.02
→ Here, 1 is the whole number,
→ 0 tenths and 2 hundredths.
So,
1.02 = 1 + 0 tenths + 2 hundredths
= 1 + (2 × \(\frac{1}{100}\))
1 + \(\frac{2}{100}\)
(c) 0.8
→ The digit 8 is in the tenths place.
So,
0.8 = 8 tenths
= (8 × \(\frac{1}{10}\))
(d) 0.362
→ 3 is in the tenths place,
→ 6 is in the hundredths place,
→ 2 is in the thousandths place.
So,
0.362 = 3 tenths + 6 hundredths + 2 thousandths
= (3 ×\(\frac{1}{10}\)) + (6 ×\(\frac{1}{100}\)) + (2 × \(\frac{1}{1000}\))
\(\frac{3}{10}\) + \(\frac{6}{100}\) + \(\frac{2}{1000}\)
3. What decimal number does each letter represent in the number line below?
Ans: There are 4 divisions between 6.4 and 6.5, so each division is one-fourth part of 0.1 or \(\frac{1}{10}\) , i.e., \(\frac{1}{40}\) = 0.025 unit.
Therefore, the second division after 6.4, denoted by ‘a’, represents the number 6.45,
while the first division after 6.5, denoted by ‘c’, represents the number 6.525,
and the second division after 6.5, denoted by ‘b’, represents the number 6.55.
4. Arrange the following quantities in descending order:
(a) 11.01, 1.011, 1.101, 11.10, 1.01
(b) 2.567, 2.675, 2.768, 2.499, 2.698
(c) 4.678 g, 4.595 g, 4.600 g, 4.656 g, 4.666 g
(d) 33.13 m, 33.31 m, 33.133 m, 33.331 m, 33.313 m
Ans:
(a) 11.01, 1.011, 1.101, 11.10, 1.01
Compare carefully — numbers with 11 are much larger.
Descending order:
11.10, 11.01, 1.101, 1.011, 1.01
(b) 2.567, 2.675, 2.768, 2.499, 2.698
Descending order:
2.768, 2.698, 2.675, 2.567, 2.499
(c) 4.678 g, 4.595 g, 4.600 g, 4.656 g, 4.666 g
Descending order:
4.678 g, 4.666 g, 4.656 g, 4.600 g, 4.595 g
(d) 33.13 m, 33.31 m, 33.133 m, 33.331 m, 33.313 m
Descending order:
33.331 m, 33.313 m, 33.31 m, 33.133 m, 33.13 m
5. Using the digits 1, 4, 0, 8, and 6 make:
(a) the decimal number closest to 30
(b) the smallest possible decimal number between 100 and 1000.
Ans: Using the digits 1, 4, 0, 8, and 6, we can make:
(a) The decimal number closest to 30 → 40.168.
(b) The smallest possible decimal number between 100 and 1000 → 104.68
6. Will a decimal number with more digits be greater than a decimal number with fewer digits?
Ans: No, a decimal number with more digits is not always greater than one with fewer digits.
The value of a decimal number depends on the place value of its digits, not on how many digits it has.
Example:
0.9 > 0.243678996.
Here, 0.9 has fewer digits but is greater.
7. Mahi purchases 0.25 kg of beans, 0.3 kg of carrots, 0.5 kg of potatoes, 0.2 kg of capsicums, and 0.05 kg of ginger. Calculate the total weight of the items she bought.
Ans: Beans = 0.25 kg
Carrots = 0.3 kg
Potatoes = 0.5 kg
Capsicums = 0.2 kg
Ginger = 0.05 kg
Total weight = 0.25 + 0.3 + 0.5 + 0.2 + 0.05
Total weight = 1.30 or 1.3 kg
8. Pinto supplies 3.79 L, 4.2 L, and 4.25 L of milk to a milk dairy in the first three days. In 6 days, he supplies 25 litres of milk. Find the total quantity of milk supplied to the dairy in the last three days.
Ans:
Milk supplied in the first three days:
= 3.79 L + 4.2 L + 4.25 L
= (3.79 + 4.2 + 4.25)
= 12.24 L
Milk supplied in six days (total):
= 25 L
The total quantity of milk supplied to the dairy in the last three days = Total milk supplied in the 6 days – Total milk supplied in the first 3 days
25 L – 12.24 L = 12.76 L
9. Tinku weighed 35.75 kg in January and 34.50 kg in February. Has he gained or lost weight? How much is the change?
Ans: Tinku’s weight in January = 35.75 kg
Tinku’s weight in February = 34.50 kg
Now, find the change:
35.75 − 34.50 = 1.25 kg
Since his February weight is less, he has lost weight.
Tinku has lost 1.25 kg of weight.
10. Extend the pattern: 5.5, 6.4, 6.39, 7.29, 7.28, 6.18, 6.17, ____, _____
Ans: 5.5 (+0.9) 6.4 (-0.01) 6.39 (+0.9) 7.29 (-0.01) 7.28 (+0.9) 8.18 (-0.01) 8.17.
Pattern alternates +0.9, -0.01, +0.9, -0.01
Next terms 8.17 + 0.9 = 9.07, 9.07 – 0.01 = 9.06
6.18, 6.17 – May be its a typing mistake.
11. How many millimeters make 1 kilometer?
Ans:
1 kilometer = 1000 meters
1 meter = 1000 millimeters
So,
1 kilometer = 1000 × 1000 = 1,000,000 millimeters
12. Indian Railways offers optional travel insurance for passengers who book e-tickets. It costs 45 paise per passenger. If 1 lakh people opt for insurance in a day, what is the total insurance fee paid?
Ans: Cost of insurance per passenger = 45 paise
Number of passengers = 1 lakh = 100,000
Now,
Total insurance fee = 45 × 100,000 = 4,500,000 paise
Convert paise into rupees:
1 rupee = 100 paise
→ 4,500,000 ÷ 100 = 45,000 rupees
13. Which is greater?
(a) \(\frac{10}{1000}\) or \(\frac{1}{10}\)
(b) One-hundredth or 90 thousandths?
(c) One-thousandth or 90 hundredths?
Ans:
(b) One-hundredth or 90 thousandths?
One-hundredth = \(\frac{1}{100}\) = 0.01
90 thousandths = \(\frac{90}{1000}\) = 0.09
0.09 > 0.01
Therefore, 90 thousandths is greater.
(c) One-thousandth or 90 hundredths?
One-thousandth = \(\frac{1}{1000}\) = 0.001
90 hundredths = \(\frac{90}{100}\) = 0.001
0.9 > 0.001
Therefore, 90 hundredths is greater.
14. Write the decimal forms of the quantities mentioned (an example is given):
(a) 87 ones, 5 tenths and 60 hundredths = 88.10
(b) 12 tens and 12 tenths
(c) 10 tens, 10 ones, 10 tenths, and 10 hundredths
(d) 25 tens, 25 ones, 25 tenths, and 25 hundredths
Ans:
(a) 87 ones, 5 tenths and 60 hundredths = 88.10
- 87 ones = 87.00
- 5 tenths = 0.5
- 60 hundredths = 0.60
87.00+0.5+0.60=88.10
(b) 12 tens and 12 tenths
= (12 × 10) + (12 × 1/10)
= 120 + 1.2
= 121.2
(c) 10 tens, 10 ones, 10 tenths, and 10 hundredths
= (10 × 10) + (10 × 1) + (10 × 1/10) + (10 × 1/100)
= 100 + 10 + 1 + 0.1
= 111.1
(d) 25 tens, 25 ones, 25 tenths, and 25 hundredths
= (25 × 10) + (25 × 1) + (25 × 1/10) + (25 × 1/100)
= 250 + 25 + 2.5 + 0.25
= 277.75
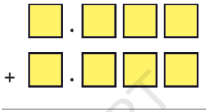
15. Using each digit 0 – 9 not more than once, fill the boxes below so that the sum is closest to 10.5:
Ans:
16. Write the following fractions in decimal form:
(a.) \(\frac{1}{2}\)
(b.) \(\frac{3}{2}\)
(c.) \(\frac{1}{4}\)
(d.) \(\frac{3}{4}\)
(e.) \(\frac{1}{5}\)
(f.) \(\frac{4}{5}\)
Ans:

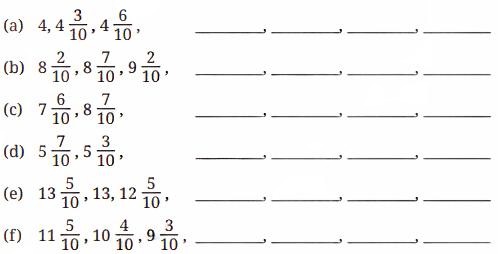

















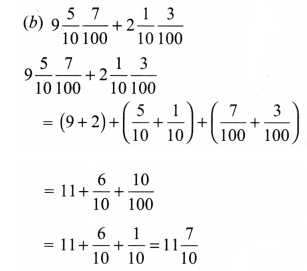
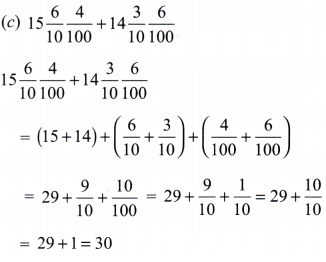
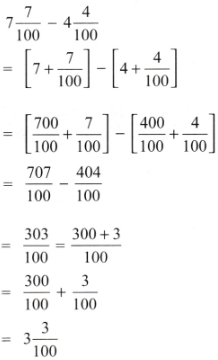
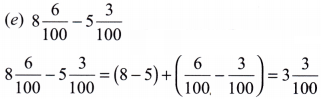
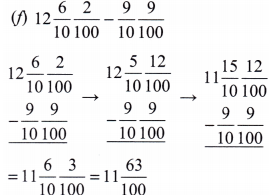


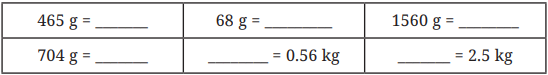
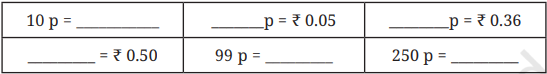
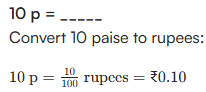

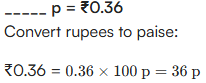
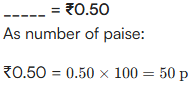
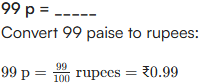
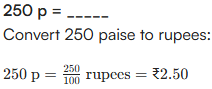


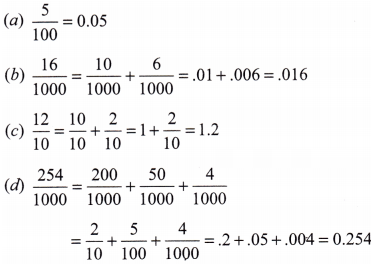
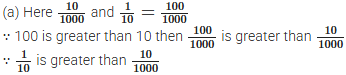
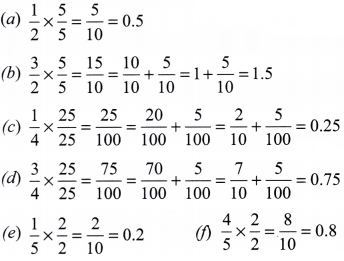

Leave a Reply