Question Answer For All Chapters – Ganita Prakash Class 7th
Figure it Out (Page 108)
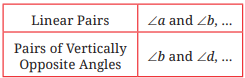
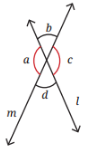
Q. List all the linear pairs and vertically opposite angles you observe in Fig. 5.3:
Ans:
Linear Pairs (adjacent angles whose sum = 180°):
- ∠a and ∠b
- ∠b and ∠c
- ∠c and ∠d
- ∠d and ∠a
Pairs of Vertically Opposite Angles (angles directly opposite each other):
- ∠a and ∠c
- ∠b and ∠d
Page 110
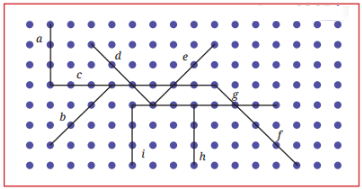
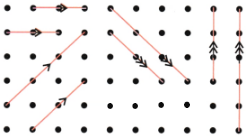
Q. Which pairs of lines appear to be parallel in Fig. 5.6 below?
Ans:
Vertical parallel lines: a, b, i
Horizontal parallel lines: c, g
Slanted (downward right): d, f
Slanted (upward right): e, h
Figure it Out (Page 113,114)
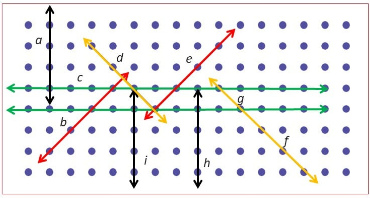
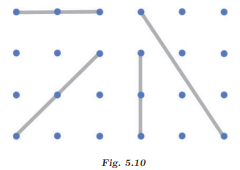
1. Draw some lines perpendicular to the lines given on the dot paper in Fig. 5.10.
Ans:
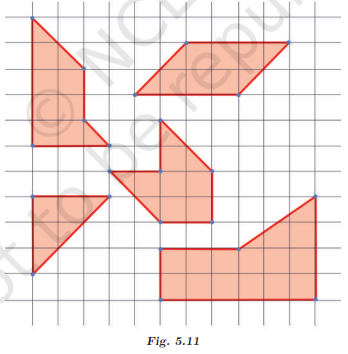
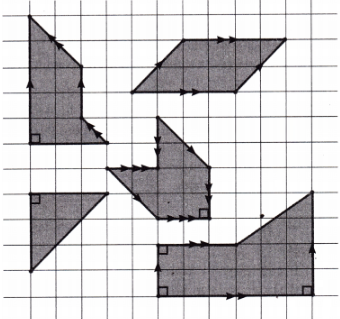
2. In Fig. 5.11, mark the parallel lines using the notation given above (single arrow, double arrow etc.). Mark the angle between perpendicular lines with a square symbol.
(a) How did you spot the perpendicular lines?
(b) How did you spot the parallel lines?
Ans:
(a) Perpendicular lines meet at right angles (90°) — like the sides of rectangles.
(b) Parallel lines never meet and are equally spaced — they run in the same direction.
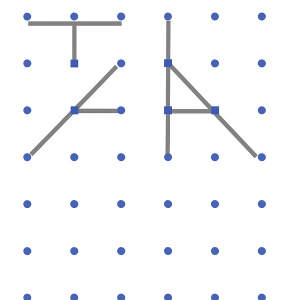
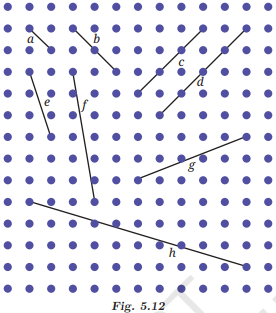
3. In the dot paper following, draw different sets of parallel lines. The line segments can be of different lengths but should have dots as endpoints.
Ans:
4. Using your sense of how parallel lines look, try to draw lines parallel to the line segments on this dot paper.
(a) Did you find it challenging to draw some of them?
(b) Which ones?
(c) How did you do it?
Ans: Do it yourself.
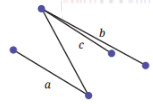
5. In Fig. 5.13, which line is parallel to line a —– line b or line c? How do you decide this?
Ans: In the given figure, line a is parallel to line c because these two lines are always the same distance apart and never meet, no matter how far they are extended.
Figure it Out (Page 119)
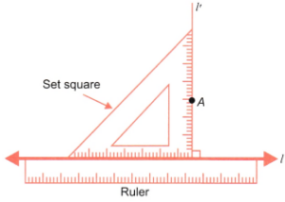
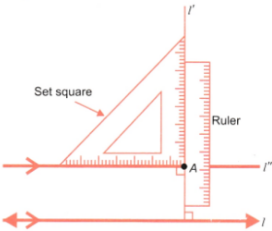
Can you draw a line parallel to l, that goes through point A? How will you do it with the tools from your geometry box? Describe your method.
Ans: We shall draw a line parallel to the given line l and passing through the point A by using a ruler and a set square.
Step 1: Place a ruler along the line as shown in the Figure.
Step 2: Slide a set square along the line l, so that its perpendicular side touches the point A. Draw a line l’ through A = as shown in the Figure.
Step 3: Place a ruler along the line l’ and slide a set square along the line l’ so that its perpendicular side touches the point A. Draw a line l” through A as shown in the Figure.
Step 4: Lines l and l” are parallel lines. Line l” is parallel to l and passes through the given point A.
Figure it Out (Pages 123-125)
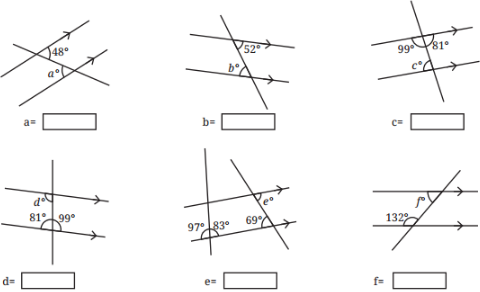
1. Find the angles marked below.
Ans:
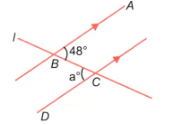
(i) In the given figure, the parallel lines are intersected by the transversal I.
∠ABC and ∠BCD are given as alternate angles.
For parallel lines, alternate angles are always equal.
Therefore, ∠ABC=∠BCD.
Given ∠ABC=48°, so a=48°.
a=48°
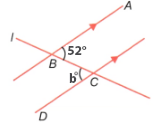
(ii) In the figure, parallel lines are intersected by the transversal l.
∠ABC=52° and ∠BCD=b°.
Since ∠ABC and ∠BCD are alternate angles, they are equal when the lines are parallel.
Therefore,
∠ABC = ∠BCD
52° = b°
b = 52°
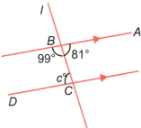
(iii) In the figure, parallel lines are intersected by the transversal l.
∠ABC=81° and ∠BCD=c°.
Since ∠ABC and ∠BCD are alternate angles, and the lines are parallel, they are equal.
Therefore,
∠ABC = ∠BCD
⇒ 81°=c°
⇒ c = 81°
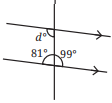
(iv) In the figure, parallel lines are intersected by the transversal l.
Here ∠d and 99° are alternate interior angles.
∠d = 99°
(v)
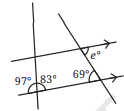
Here ∠e and 69° are alternate interior angles.
∠d = 69°
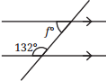
(vi)
Here ∠f and 132° are interior angles on same side of transversal.
So, their sum is 180°
∠f + 132° = 180°
∴∠f = 180°- 132°
∴ f = 48°
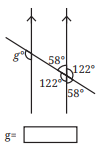
(vii)
Here ∠g and 122° are corresponding angles.
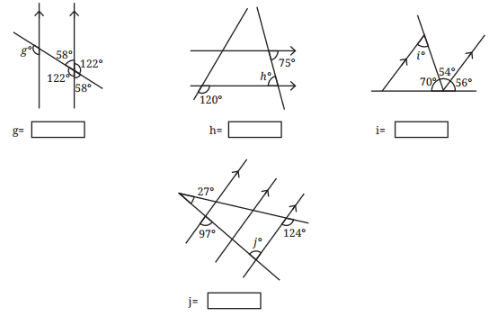
∠g = 122°
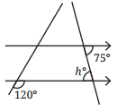
(viii)
Here ∠h and 75° are alternate interior angles.
∠h = 75°
(ix)
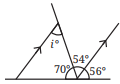
Here ∠i and 54° are alternate interior angles.
∠h = 54°
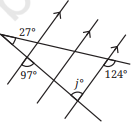
(x)
Here ∠j and 97° are alternate interior angles.
∠h = 97°
2. Find the angle represented by a.
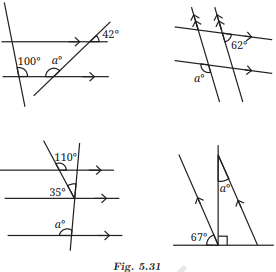
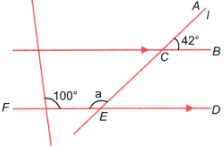
Ans: (i)
Here, ∠ACB=42° and ∠CEF=a°.
∠ACB and ∠BCE form a linear pair, so
∠ACB + ∠BCE=180°
⇒ 42°+∠BCE = 180°
⇒ ∠BCE = 180°−42° = 138°
Now, ∠BCE and ∠CEF are alternate angles,
therefore, ∠BCE=∠CEF.
Hence, 138°=a°
⇒ a = 138°
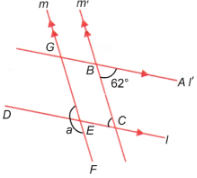
(ii) In the figure, parallel lines l, l’ are intersected by parallel transversals m and m’.
Here, ∠ABC = 62° and ∠DEE = a°.
∠ABC and ∠BCE are alternate angles.
∴ ∠ABC = ∠BCE
⇒ 62° = ∠BCE
∠BCE and ∠GED are corresponding angles.
∴ ∠BCE = ∠GED
⇒ 62° = ∠GED
∠GED and ∠DEF are linear angles.
∴ ∠GED + ∠DEF = 180°
62° + a = 180°
⇒ a = 180° – 62° = 118°.
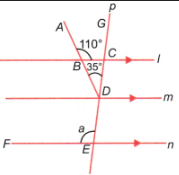
(iii) In the figure, parallel lines l, m, and n are intersected by the transversal p.
Here, ∠ABC = 110°, ∠BDC = 35° and ∠DEF = a.
∠ABC and ∠CBD are linear angles.
∴ ∠ABC + ∠CBD = 180°
⇒ 110° + ∠CBD = 180°
⇒ ∠CBD = 180° – 110° = 70°
In ∆BCD, we have
∠CBD + ∠BCD + ∠CDB = 180°.
∴ 70° + ∠BCD + 35° = 180°
⇒ ∠BCD = 180° – 105° = 75°
∠GCB and ∠BCD are linear angles.
∴ ∠GCB + ∠BCD = 180°
⇒ ∠GCB + 75° = 180°
⇒ ∠GCB = 180° – 75° = 105°
∠GCB and ∠DEF are corresponding angles.
∴ ∠GCB = ∠DEF
⇒ 105° = a
a = 105°
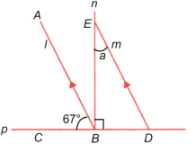
(iv) In the figure, parallel lines l and m are intersected by the transversals n and p.
We have ∠ABC = 67°, ∠DBE = 90° and ∠BED = a.
∠ABC, ∠ABE, and ∠DBE are linear angles.
∴ ∠ABC + ∠ABE + ∠DBE = 180°
⇒ 67° + ∠ABE + 90° = 180°
⇒ ∠ABE = 180° – 157° = 23°
∠ABE and ∠BED are alternate angles.
∴ ∠ABE = ∠BED
⇒ 23° = a
⇒ a = 23°.
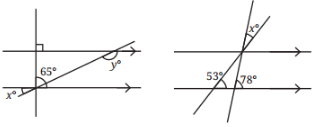
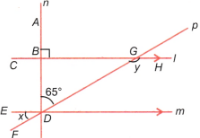
3. In the figures below, what angles do x and y stand for?
Ans:
(i) In the figure, parallel lines l and m are intersected by transversals n and p.
We have ∠ABG = 90°, ∠BDG = 65°, ∠EDF = x and ∠DGH = y.
∠ABG and ∠DBG are linear angles.
∴ ∠ABG + ∠DBG = 180°
90° + ZDBG =180°
⇒ ∠DBG = 180° – 90° = 90°
And ∠DBG and ∠BDE are alternate angles.
∴ ∠DBG = ∠BDE
⇒ 90° = ∠BDE
∠EDF, ∠BDE, and ∠BDG are linear angles.
∴ ∠EDF + ∠BDE + ∠BDG = 180°
⇒ x + 90° + 65° = 180°
⇒ x = 180° – 155° = 25°
∠EDF and ∠BGD are corresponding angles.
∴ ∠EDF = ∠BGD
⇒ x = ∠BGD
⇒ ∠BGD = 25°
∠BGD and ∠DGH are linear angles.
∴ ∠BGD + ∠DGH = 180°
⇒ 25° + y = 180°
⇒ y = 180° – 25° = 155°
∴ x = 25° and y = 155°.
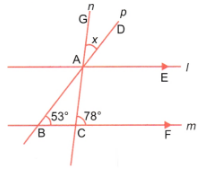
(ii) In the figure, parallel lines l and m are intersected by transversals n and p.
We have ∠GAD = x, ∠ABC = 53°, and ∠ACF = 78°.
∠DAE and ∠ABC are corresponding angles.
∴ ∠DAE = ∠ABC
⇒ ∠DAE = 53°
∠GAE and ∠ACF are corresponding angles.
∴ ∠GAE = ∠ACF
∠GAE = 78°
Also, ∠GAE = ∠GAD + ∠DAE
∴ 78° = x + 53°
⇒ x = 78° – 53° = 25°
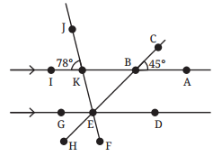
4. In Fig. 5.33, ∠ABC = 45° and ∠IKJ = 78°. Find angles ∠GEH, ∠HEF, ∠FED
Ans:
- ∠ABC = 45°
- ∠IKJ = 78°
Lines IA ∥ HF (the two horizontal lines)
Lines HC and JF act as transversals
Vertically opposite angles:
At intersection of IA and HC,
∠ABC = ∠KBE = 45°
At intersection of JF and IA,
∠IKJ = ∠BKE = 78°
Corresponding angles (since IA ∥ HF):
∠KBE = ∠GEH = 45°
∠BKE = ∠FED = 78°
Linear pair on line H–E–F:
∠GEH+∠HEF+∠FED=180°
Substituting:
45°+∠HEF+78°=180°
∠HEF=180°−123°=57°
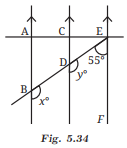
5. In Fig. 5.34, AB is parallel to CD and CD is parallel to EF. Also, EA is perpendicular to AB. If ∠BEF = 55°, find the values of x and y.
Ans:
Given AB is parallel to CD and CD is parallel to EF.
So, AB is parallel to EF.
Now, EF is parallel to CD, and DE is a transversal.
So, y° + 55° = 180° [Sum of interior angles]
y = 125°
Now, AB is parallel to CD, and BD is a transversal.
So, x° =y° = 125° [Corresponding Angles]
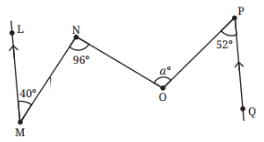
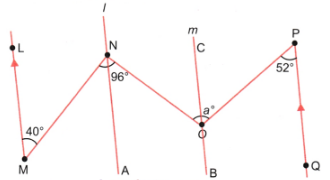
6. What is the measure of angle ∠NOP in Fig. 5.35?
[Hint: Draw lines parallel to LM and PQ through points N and O.]
Ans:
∠LMN and ∠MNA are alternate angles
- ∴∠LMN=∠MNA
- ⇒40 = ∠MNA
∠MNO is the sum of ∠MNA and ∠ANO
- ∠MNO=∠MNA+∠ANO
Substitute the known values:
- 96∘=40∘+∠ANO
- ⇒∠ANO=96∘ −40∘ =56∘
∠ANO and ∠NOC are alternate angles
- ∴∠ANO = ∠NOC
- ⇒∠NOC=56∘
∠COP and ∠OPQ are alternate angles
- ∴∠COP = ∠OPQ
- ⇒∠COP=52∘
∠NOP is the sum of ∠NOC and ∠COP
- ∠NOP = ∠NOC+∠COP
- Substitute the known values:
- a = 56∘ + 52∘ = 108∘

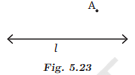


Leave a Reply