Page. 15.3 Ex.15.1
Q1.
Answer :
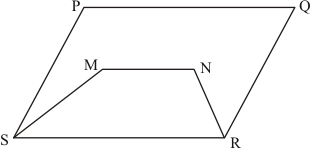
GIVEN: Here in the question figure 1 to 6 are shown.
To Find :
(1) The figures which lie on the same base and between the same parallels.
(2) Write the common base and parallels.
As we know that ‘Two geometric figures are said to be on the same base and between the same parallels, if they have a common side(base) and the vertices (or vertex) opposite to the common base of each figure lie on a line parallel to the base.’
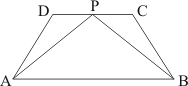
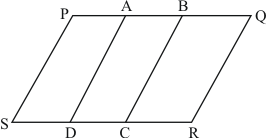
(1) ΔAPB and trapezium ABCD are on the same base CD and between the same parallels AB and CD.
(2) Parallelograms ABCD and APQD are on the same base AD and between the same parallels AD and BQ.
(3) Parallelogram ABCD and ΔPQR are between the same parallels AD and BC,. but they are not on the same base AD
(4) Parallelogram ABCD and ΔPQR are between the same parallels AD and BC,. but they are not on the same base AD .
(5) ΔQRT and Parallelogram PQRS are on the same base QR and between the same parallels PS and QR.
(6) Parallelogram PQRS, AQRD, and BCQR are between the same parallels. Also Parallelogram PQRS, BPSC and APSD are between the same parallels.
Page. 15.14 Ex.15.2
Q1.
Answer :
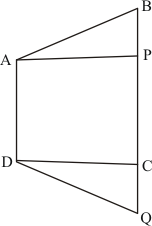
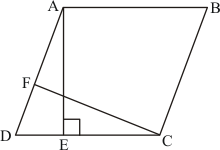
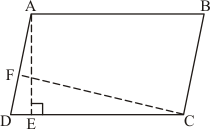
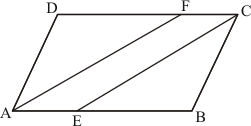
Given: Here in the question it is given
(1) ABCD is a parallelogram,
(2) and
(3) , AB = 16 cm
(4) AE = 8cm
(5) CF = 10cm
To Find : AD =?
Calculation: We know that formula for calculating the
Therefore,
Area of paralleogram ABCD = DC × AE (Taking base as DC and Height as AE )
Area of paralleogram ABCD = AB × AE (AB = DC as opposite side of the parallelogram are equal)
Therefore,
Area of paralleogram ABCD = 16 × 8 ……(1)
Taking the base of Parallelogram ABCD as AD we get
Area of paralleogram ABCD = AD × CF (taking base as AD and height as CF)
Area of paralleogram ABCD = AD × 10 ……(2)
Since equation 1 and 2 both represent the Area of the same Parallelogram ABCD , both should be equal.
Hence fro equation (1) and (2),
This means that,
Hence we get the result as
Q2.
Answer :
Given: Here in the question it is given that
(1) ABCD is a parallelogram,
(2) and
(3)
(4) AD = 6 cm
(5) AE = 8cm
(6) CF = 10cm
To Find : AB =?
Calculation: We know that formula for calculating the
Area of paralleogram = base × height
Therefore,
Area of paralleogram ABCD = DC × AE (Taking base as DC and Height as AE )
Area of paralleogram ABCD = AB × AE (AB = DC as opposite side of the parallelogram are equal)
Therefore, Area of paralleogram ABCd = 16 × 8
Area of Parallelogram ABCD = AB× 8 ……(1)
Taking the base of Parallelogram ABCD as AD we get
Area of paralleogram ABCD = AD × CF (taking base as AD and height as CF)
Area of paralleogram ABCD = 6 × 10 ……(2)
Since equation 1and 2 both represent the Area of the same Parallelogram ABCD , both should be equal.
Hence equation 1 is equal to equation 2
Which means that,
Hence we got the measure of AB equal to
Q3.
Answer :
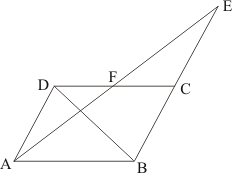
Given: Here in the question it is given that
(1) Area of paralleogram ABCD = 124 cm2
(2) E is the midpoint of AB, which means
(3) F is the midpoint of CD, which means
To Find : Area of Parallelogram AEFD
Calculation: We know that formula for calculating the
Area of Parallelogram = base × height
Therefore,
Area of paralleogram ABCD = AB × AD (Taking base as AB and Height as AD ) ……(1)
Therefore,
Area of paralleogram AEFD = AE × AD (Taking base as AB and Height as AD ) ……(2)
(
)
= Area of Parallelogram ABCD (from equation1)
Hence we got the result Area of Parallelogram AEFD
Q4.
Answer :
Given: Here in the question it is given that
(1) ABCD is a Parallelogram
To Prove :
(1)
(2)
(3)
(4)
Construction: Draw
Calculation: We know that formula for calculating the
Area of Parallelogram = base × height
Area of paralleogram ABCD = BC × AE (Taking base as BC and Height as AE ……(1)
We know that formula for calculating the
Area of ΔADC = Base × Height
(AD is the base of ΔADC and AE is the height of ΔADC)
= Area of Parallelogram ABCD (from equation1)
Hence we get the result
Similarly we can show that
(2)
(3)
(4)
Page. 15.40 Ex.15.3
Q1.
Answer :
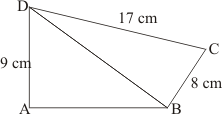
Given: Here from the given figure we get
(1) ABCD is a quadrilateral with base AB,
(2) ΔABD is a right angled triangle
(3) ΔBCD is a right angled triangle with base BC right angled at B
To Find: Area of quadrilateral ABCD
Calculation:
In right triangle ΔBCD, by using Pythagoreans theorem
.So
In right triangle ABD
Hence we get Area of quadrilateral ABCD =
Q2.
Answer :
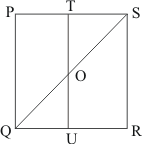
Given: Here from the given figure we get
(1) PQRS is a square,
(2) T is the midpoint of PS which means
(3) U is the midpoint of PS which means
(4) QU = 8 cm
To find: Area of ΔOTS
Calculation:
Since it is given that PQ = 8 cm. So
Since T and U are the mid points of PS and QR respectively. So
Therefore area of triangle OTS is equals to
Hence we get the result that Area of triangle OTS is
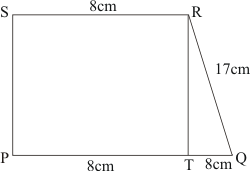
Q3.
Answer :
Given:
(1) PQRS is a trapezium in which SR||PQ..
(2) PT = 5 cm.
(3) QT = 8 cm.
(4) RQ = 17 cm.
To Calculate: Area of trapezium PQRS.
Calculation:
In triangle
.So
No area of rectangle PTRS
Therefore area of trapezium PQRS is
Hence the answer is
Q4.
Answer :
Given: In figure:
(1) ∠AOB = 90°
(2) AC = BC,
(3) OA = 012 cm,
(4) OC = 6.5 cm.
To find: Area of ΔAOB
Calculation:
It is given that AC = BC where C is the mid point of AB
We know that the mid point of hypotenuse of right triangle is equidistant from the vertices
Therefore
CA = BC = OC
⇒ CA = BC = 6.5
⇒ AB = 2 × 6.5 = 13 cm
Now inn triangle OAB use Pythagoras Theorem
So area of triangle OAB
Hence area of triangle is
Q5.
Answer :
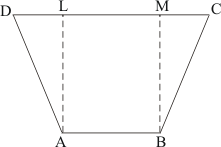
Given: Here from the given figure we get
(1) ABCD is a trapezium
(2) AB = 7 cm,
(3) AD = BC = 5 cm,
(4) DC = x cm
(5) Distance between AB and DC is 4 cm
To find:
(a) The value of x
(b) Area of trapezium
Construction: Draw AL⊥ CD, and BM ⊥ CD
Calculation:
Since AL ⊥ CD, and BM ⊥ CD
Since distance between AB and CD is 4 cm. So
AL = BM = 4 cm, and LM = 7 cm
In triangle ADL use Pythagoras Theorem
Similarly in right triangle BMC use Pythagoras Theorem
Now
We know that,
We get the result as
Area of trapezium is
Q6.
Answer :
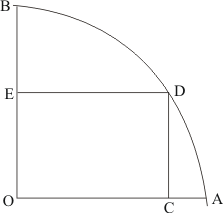
Given: Here from the given figure we get
(1) OCDE is a rectangle inscribed in a quadrant of a circle with radius 10cm,
(2) OE = 2√5cm
To find: Area of rectangle OCDE.
Calculation:
In right triangle ΔODE use Pythagoras Theorem
We know that,
Hence we get the result as area of Rectangle OCDE =
Page. 15.41 Ex.15.3
Q7.
Answer :
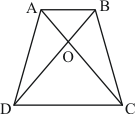
Given:
ABCD is a trapezium with AB||DC
To prove: Area of ΔAOD = Area of ΔBOC
Proof:
We know that ‘triangles between the same base and between the same parallels have equal area’
Here ΔABC and ΔABD are between the same base and between the same parallels AB and DC.
Therefore
Hence it is proved that
Q8.
Answer :
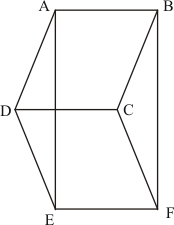
Given:
(1) ABCD is a parallelogram,
(2) ABFE is a parallelogram
(3) CDEF is a parallelogram
To prove: Area of ΔADE = Area of ΔBCF
Proof:
We know that,” opposite sides of a parallelogram are equal”
Therefore for
Parallelogram ABCD, AD = BC
Parallelogram ABFE, AE = BF
Parallelogram CDEF, DE = CF.
Thus, in ΔADE and ΔBCF, we have
So be SSS criterion we have
This means that
Hence it is proved that
Q9.
Answer :
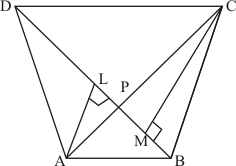
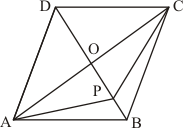
Given:
(1) ABCD is a quadrilateral,
(2) Diagonals AC and BD of quadrilateral ABCD intersect at P.
To prove: Area ofΔ APB ×Area of ΔCPD = Area of ΔAPD × Area of ΔBPC
Construction: Draw AL perpendicular to BD and CM perpendicular to BD
Proof:
We know that
Area of triangle = × base× height
Area of ΔAPD = × DP × AL …… (1)
Area of ΔBPC = × CM × BP …… (2)
Area of ΔAPB = × BP × AL …… (3)
Area of ΔCPD = × CM × DP …… (4)
Therefore
Hence it is proved that
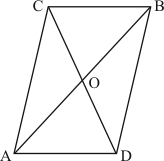
Q10.
Answer :
Given:
(1) ABC and ABD are two triangles on the same base AB,
(2) CD bisect AB at O which means AO = OB
To Prove: Area of ΔABC = Area of ΔABD
Proof:
Here it is given that CD bisected by AB at O which means O is the midpoint of CD.
Therefore AO is the median of triangle ACD.
Since the median divides a triangle in two triangles of equal area
Therefore Area of ΔCAO = Area of ΔAOD …… (1)
Similarly for Δ CBD, O is the midpoint of CD
Therefore BO is the median of triangle BCD.
Therefore Area of ΔCOB = Area of ΔBOD …… (2)
Adding equation (1) and (2) we get
Area of ΔCAO + Area of ΔCOB = Area of ΔAOD + Area of ΔBOD
⇒ Area of ΔABC = Area of ΔABD
Hence it is proved that
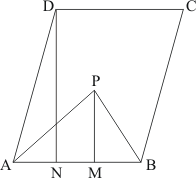
Q11.
Answer :
Given: Here from the question we get
(1) ABCD is a parallelogram
(2) P is any point in the interior of parallelogram ABCD
To prove:
Construction: Draw DN perpendicular to AB and PM perpendicular AB
Proof: Area of triangle = × base× height
Area of ΔAPB = × AB × PM …… (1)
Also we know that: Area of parallelogram = base× height
Area of parallelogram ABCD = AB × DN …… (2)
Now PM < DN (Since P is a point inside the parallelogram ABCD)
Hence it is proved that
Q12.
Answer :
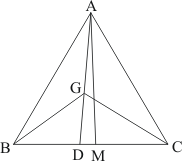
Given:
(1) ABC is a triangle
(2) AD is the median of ΔABC
(3) G is the midpoint of the median AD
To prove:
(a) Area of Δ ADB = Area of Δ ADC
(b) Area of Δ BGC = 2 Area of Δ AGC
Construction: Draw a line AM perpendicular to AC
Proof: Since AD is the median of ΔABC.
Therefore BD = DC
So multiplying by AM on both sides we get
In ΔBGC, GD is the median
Since the median divides a triangle in to two triangles of equal area. So
Area of ΔBDG = Area of ΔGCD
⇒ Area of ΔBGC = 2(Area of ΔBGD)
Similarly In ΔACD, CG is the median
⇒ Area of ΔAGC = Area of ΔGCD
From the above calculation we have
Area of ΔBGD = Area of ΔAGC
But Area of ΔBGC = 2(Area of ΔBGD)
So we have
Area of ΔBGC = 2(Area of ΔAGC)
Hence it is proved that
(1)
(2)
Q13.
Answer :
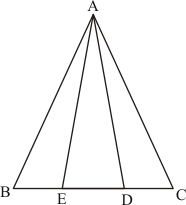
Given:
(1) ABC is a triangle
(2) D is a point on BC such that BD = 2DC
To prove: Area of ΔABD = 2 Area of ΔAGC
Proof:
In ΔABC, BD = 2DC
Let E is the midpoint of BD. Then,
BE = ED = DC
Since AE and AD are the medians of ΔABD and ΔAEC respectively
and
The median divides a triangle in to two triangles of equal area. So
Hence it is proved that
Q14.
Answer :
Given: Here from the given figure we get
(1) ABCD is a parallelogram
(2) BD and CA are the diagonals intersecting at O.
(3) P is any point on BO
To prove:
(a) Area of ΔADO = Area ofΔ CDO
(b) Area of ΔAPB = Area ofΔ CBP
Proof: We know that diagonals of a parallelogram bisect each other.
O is the midpoint of AC and BD.
Since medians divide the triangle into two equal areas
In ΔACD, DO is the median
Area of ΔADO = Area ofΔ CDO
Again O is the midpoint of AC.
In ΔAPC, OP is the median
⇒ Area of ΔAOP = Area of ΔCOP …… (1)
Similarly O is the midpoint of AC.
In ΔABC, OB is the median
⇒ Area of ΔAOB = Area of ΔCOB …… (2)
Subtracting (1) from (2) we get,
Area of ΔAOB − Area of ΔAOP = Area of ΔCOB − Area of ΔCOP
⇒ Area of ΔABP = Area of ΔCBP
Hence it is proved that
(a)
(b)
Q15.
Answer :
Given: Here from the given figure we get
(1) ABCD is a parallelogram with base AB,
(2) BC is produced to E such that CE = BC
(3) AE intersects CD at F
(4) Area of ΔDFB = 3 cm
To find:
(a) Area of ΔADF = Area of ΔECF
(b) Area of parallelogram ABCD
Proof: Δ ADF and ΔECF, we can see that
∠ADF = ∠ECF (Alternate angles formed by parallel sides AD and CE)
AD = EC
∠DFA = ∠CFA (Vertically opposite angles)
(ASA condition of congruence)
As
DF = CF
Since DF = CF. So BF is a median in ΔBCD
Since median divides the triangle in to two equal triangles. So
Since .So
Hence Area of parallelogram ABCD
Hence we get the result
(a)
(b)
Page. 15.42 Ex.15.3
Q16.
Answer :
Given:
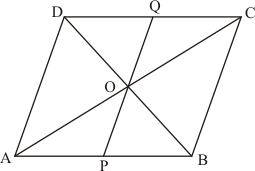
(1) Diagonals AC and BD of a parallelogram ABCD intersect at point O.
(2) A line through O intersects AB at P point.
(3) A line through O intersects DC at Q point.
To find: Area of (ΔPOA) = Area of (ΔQOC)
Proof:
From ΔPOA and ΔQOC we get that
=
OA = OC
=
So, by ASA congruence criterion, we have
So
Area (ΔPOA) = Area (ΔQOC)
Hence it is proved that
Q17.
Answer :
Given:
(1) ABCD is a parallelogram.
(2) E is a point on BA such that BE = 2EA
(3) F is a point on DC such that DF = 2FC.
To find:
Area of parallelogram
Proof: We have,
BE = 2EA and DF = 2FC
AB − AE = 2AE and DC − FC = 2FC
AB = 3AE and DC = 3FC
AE =
AB and FC =
DC
AE = FC [since AB = DC]
Thus, AE || FC such that AE = FC
Therefore AECF is a parallelogram.
Clearly, parallelograms ABCD and AECF have the same altitude and
AE = AB.
Therefore
Hence proved that
Q18.
Answer :
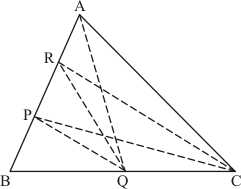
Given:
(1) In a triangle ABC, P is the mid-point of AB.
(2) Q is mid-point of BC.
(3) R is mid-point of AP.
To prove:
(a) Area of ΔPBQ = Area of ΔARC
(b) Area of ΔPRQ = Area of ΔARC
(c) Area of ΔRQC = Area of ΔABC
Proof: We know that each median of a triangle divides it into two triangles of equal area.
(a) Since CR is a median of ΔCAP
Therefore …… (1)
Also, CP is a median of ΔCAB.
Therefore …… (2)
From equation (1) and (2), we get
Therefore …… (3)
PQ is a median of ΔABQ
Therefore
Since
Put this value in the above equation we get
…… (4)
From equation (3) and (4), we get
Therefore …… (5)
(b)
…… (6)
…… (7)
From equation (6) and (7)
…… (8)
From equation (7) and (8)
(c)
= …… (9)
Q19.
Answer :
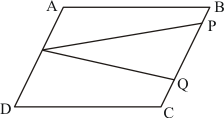
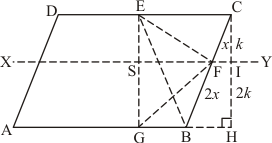
Given:
ABCD is a parallelogram
G is a point such that AG = 2GB
E is a point such that CE = 2DE
F is a point such that BF = 2FC
To prove:
(i)
(ii)
(iii)
(iv)
What portion of the area of parallelogram ABCD is the area of ΔEFG
Construction: draw a parallel line to AB through point F and a perpendicular line to AB through
PROOF:
(i) Since ABCD is a parallelogram,
So AB = CD and AD = BC
Consider the two trapeziums ADEG and GBCE:
Since AB = DC, EC = 2DE, AG = 2GB
, and
, and
So, and
Since the two trapeziums ADEG and GBCE have same height and their sum of two parallel sides are equal
Since
So
Hence
(ii) Since we know from above that
. So
Hence
(iii) Since height of triangle EFC and triangle EBF are equal. So
Hence
(iv) Consider the trapezium in which
![]() (From (iii))
(From (iii))
Now from (ii) part we have
(v) In the figure it is given that FB = 2CF. Let CF = x and FB = 2x
Now consider the tow triangles CFI and CBH which are similar triangles
So by the property of similar triangle CI = k and IH = 2k
Now consider the triangle EGF in which
Now
(Multiply both sides by 2)
…… (2)
From (1) and (2) we have
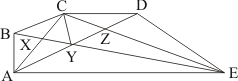
Q20.
Answer :
Given:
(1) CD||AE.
(2) CY||BA.
To find:
(i) Name a triangle equal in area of ΔCBX.
(ii) .
(iii) .
Proof:
(i) Since triangle BCY and triangle YCA are on the same base and between same parallel, so their area should be equal. Therefore
Therefore area of triangle CBX is equal to area of triangle AXY
(ii) Triangle ADE and triangle ACE are on the same base AE and between the same parallels AE and CD.
(iii) Triangle ACY and BCY are on the same base CY and between same parallels CY and BA. So we have
Now we know that
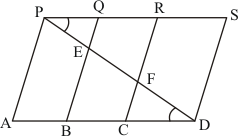
Q21.
Answer :
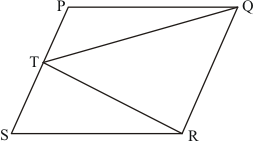
Given:
(i) PSDA is a parallelogram.
(ii) .
(iii)
To find:
Proof:
Since AP||BQ||CR||DS and AD||PS
So PQ = CD …… (1)
In ΔBED, C is the mid point of BD and CF||BE
This implies that F is the mid point of ED. So
EF = FD …… (2)
In ΔPQE and ΔCFD, we have
PE = FD
, and [Alternate angles]
PQ = CD.
So, by SAS congruence criterion, we have
ΔPQE = ΔDCF
Hence proved that
Q22.
Answer :
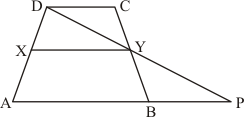
Given: ABCD IS A trapezium in which
(a) AB||DC
(b) DC = 40 cm
(c) AB = 60 cm
(d) X is the midpoint of AD
(e) Y is the midpoint of BC
To prove:
(i) XY = 50 cm
(ii) DCYX is a trapezium
(iii)
Construction: Join DY and produce it to meet AB produced at P.
Proof:
(i) In ΔBYP and ΔCYD
Y is the midpoint of BC also X is the midpoint of AD
Therefore XY||AP and
(ii) We have proved above that XY||AP
XY|| AP and AB||DC (Given in question)
XY|| DC
(iii) Since X and Y are the midpoints of AD and BC respectively.
Therefore DCYX and ABYX are of the same height say h cm.
Q23.
Answer :
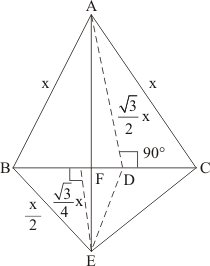
Given:
(a) ΔABC and Δ BDE are two equilateral triangles
(b) D is the midpoint of BC
(c) AE intersect BC in F.
To prove:
(i)
(ii)
(iii)
(iv)
(v)
(vi)
Proof: Let AB = BC = CA = x cm.
Then BD = = DE = BE
(i) We have
(ii) We Know that ΔABC and ΔBED are equilateral triangles
BE||AC
(iii) We Know that ΔABC and ΔBED are equilateral triangles
AB || DE
(iv) Since ED is a median of Δ BEC
(v) We basically want to find out FD. Let FD = y
Since triangle BED and triangle DEA are on the same base and between same parallels ED and BE respectively. So
Since altitude of altitude of any equilateral triangle having side x is
So
…… (1)
Now
…… (2)
From (1) and (2) we get
(vi) Now we know y in terms of x. So
……. (3)
…… (4)
From (3) and (4) we get
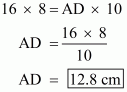
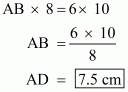
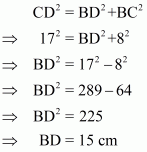
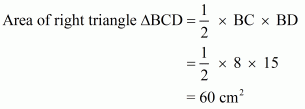
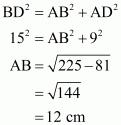
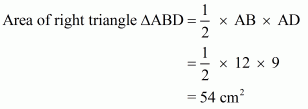
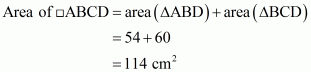
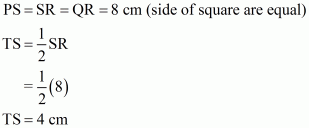
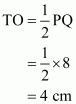
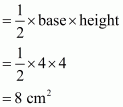
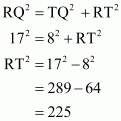
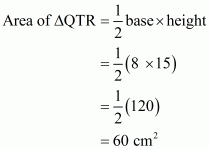
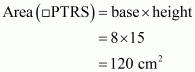
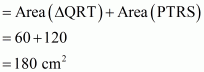
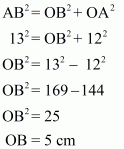
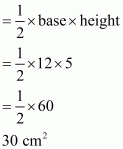
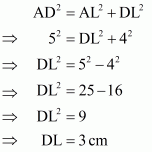
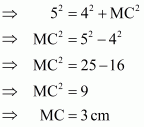
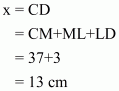
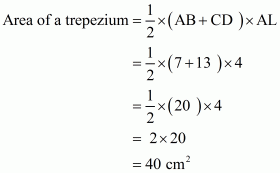
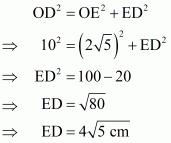
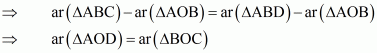
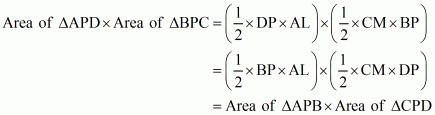
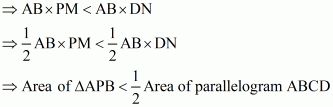
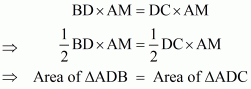
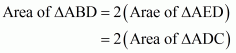
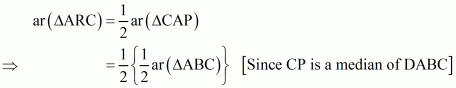
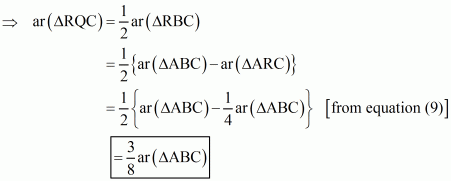
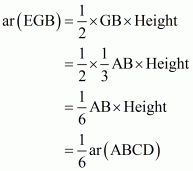
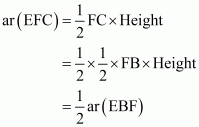
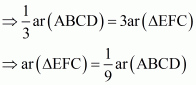
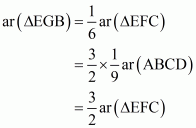
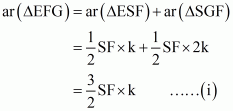
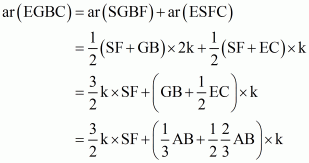
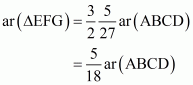
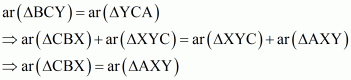

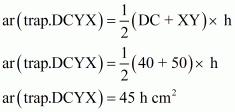
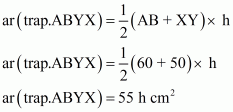
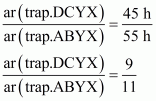
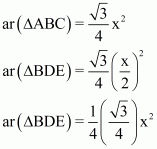
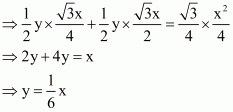
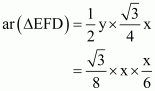
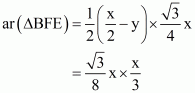
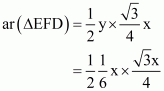

Leave a Reply