Algebraic Identities
Page no. 4.11 Ex. 4.2
Q1.
Answer :
In the given problem, we have to find expended form
(i) Given
We shall use the identity
By applying in identity we get
Hence the expended form of
is
(ii) Given
We shall use the identity
Here
By applying in identity we get
Hence the expended form of is
(iii) Given
We shall use the identity
Here
By applying in identity we get
Hence the expended form of is
.
(iv) Given
We shall use the identity
Here
By applying in identity we get
Hence the expended form of is
(v) Given
We shall use the identity
Here
By applying in identity we get
Hence the expended form of is
.
(vi) Given
We shall use the identity
Here
By applying in identity we get
Hence the expended form of is
.
(vii) Given
We shall use the identity
Here
By applying in identity we get
Hence the expended form ofis
.
(viii) Given
We shall use the identity
Here
By applying in identity we get
Hence the expended form of 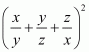
(ix) Given
We shall use the identity
Here
By applying in identity we get
Hence the expended form of is
(x) Given
We shall use the identity
Here
By applying in identity we get
Hence the expended form of is
(xi) Given
We shall use the identity
Here
By applying in identity we get
Hence the expended form of is
(xii) Given
We shall use the identity
Here
By applying in identity we get
Hence the expended form of is
.
Q2.
Answer :
In the given problem, we have to simplify the expressions
(i) Given
By using identity
Hence the equation becomes
Taking 2 as common factor we get
Hence the simplified value of is
(ii) Given
By using identity
Hence the equation becomes
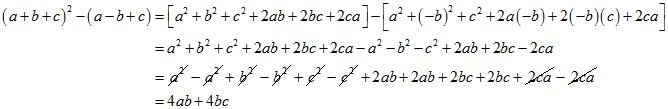
Taking 4 as common factor we get
Hence the simplified value of is
.
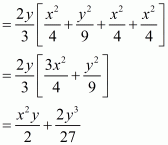
(iii) Given
By using identity , we have
Taking 3 as a common factor we get
Hence the value ofis
.
(iv) Given
By using identity , we get
By canceling the opposite terms, we get
Taking as common a factor we get,
Hence the value of is
(v) We have
Using formula, we get
By canceling the opposite terms, we get
Taking as common factor we get
Hence the value of is
.
Page no. 4.12 Ex. 4.2
Q3.
Answer :
Answer :
In the given problem, we have to find value of
Given and
Squaring the equation, we get
Now putting the value of in above equation we get,
Taking 2 as common factor we get
Hence the value of is
.
Q4.
Answer :
In the given problem, we have to find value of
Given
Multiply equation with 2 on both sides we get,
Now adding both equation and
we get
We shall use the identity
Hence the value of is
.
Q5.
Answer :
In the given problem, we have to find value of
Given
Squaring both sides of we get,
Substituting in above equation we get,
Hence the value of is
.
Q6.
Answer :
In the given problem, we have to find value of
Given
We have
This equation can also be written as
Using the identity
Hence the value of is
.
Q7.
Answer :
In the given problem, we have to simplify the value of each expression
(i) Given
We shall use the identity for each bracket
By arranging the like terms we get
Now adding or subtracting like terms,
Hence the value of is
(ii) Given
We shall use the identity for expanding the brackets
Now arranging liked terms we get,
Hence the value of is
(iii) Given
We shall use the identity for each brackets
Canceling the opposite term and simplifies
Hence the value of is
.
Page no. 4.19 Ex. 4.3
Q1.
Answer :
In the given problem, we have to find cube of the binomial expressions
(i) Given
We shall use the identity
Here
By applying the identity we get
Hence cube of the binomial expression is
(ii) Given
We shall use the identity
Here
By applying the identity we get
Hence cube of the binomial expression of is
(iii) Given
We shall use the identity
Here,
By applying identity we get
Hence cube of the binomial expression of is
(iv) Given
We shall use the identity
Here
By applying in identity we get
Hence cube of the binomial expression of is
.
Q2.
In the given problem, we have to simplify equation
(i) Given
We shall use the identity
Here
By applying identity we get
Hence simplified form of expression is
.
(ii) Given
We shall use the identity
Here
By applying identity we get
By rearranging the variable we get
Hence the simplified value of is
(iii) Given
We shall use the identity
Here
By applying identity we get
By rearranging the variable we get,
Hence the simplified value of is
(iv) Given
We shall use the identity
Here
By applying the identity we get
By rearranging the variable we get,
Hence the simplified value of is
.
Q3.
Answer :
In the given problem, we have to find the value of
Given
We shall use the identity
Here putting,
Hence the value of is
.
Q4.
Answer :
In the given problem, we have to find the value of
Given
We shall use the identity
Here putting,
Hence the value of is
.
Q5.
Answer :
In the given problem, we have to find the value of
Given
We shall use the identity
Here putting,
Hence the value of is
Q6.
In the given problem, we have to find the value of
Given
We shall use the identity
Here putting,
Hence the value of is
Q7.
Answer :
In the given problem, we have to find the value of
Given
We shall use the identity
Here putting,
Hence the value of is
.
Q8.
Answer :
In the given problem, we have to find the value of
Given
We shall use the identity
Here putting,
In order to find we are using identity
Here and
Hence the value of is
.
Q9.
Answer :
In the given problem, we have to find the value of
Given
We shall use the identity
Here putting,
In order to find we are using identity
Here
and
Hence the value of is
.
Q10.
Answer :
In the given problem, we have to find the value of
Given,
In order to find we are using identity
Here putting,
Hence the value of is
.
Q11.
Answer :
In the given problem, we have to find the value of
Given,
In order to find we are using identity
Here putting,,
Hence the value of is
.
Page no. 4.20 Ex. 4.3
Q12.
Given
We shall use the identity
Here putting,
In order to find we are using identity
In order to find we are using identity
Here
and
Hence the value of is
.
Q13.
Answer :
In the given problem, we have to find the value of numbers
(i) Given
In order to find we are using identity
We can write as
Hence where
The value of is
(ii) Given
In order to find we are using identity
We can write as
Hence where
The value of is
(iii) Given
In order to find we are using identity
We can write 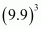
Hence where
The value of is
(iv) Given
In order to find we are using identity
We can write as
Hence where
The value of is
(v) Given
In order to find we are using identity
We can write as
Hence where
The value of is
(vi) Given
In order to find we are using identity
We can write as
Hence where
The value of is
.
Q14.
Answer :
In the given problem, we have to find the value of numbers
(i) Given
We can write as
We shall use the identity
Here
Hence the value of is
(ii) Given
We can write as
We shall use the identity
Here
Hence the value of is
(iii) Given
We can write as
We shall use the identity
Here
Hence the value of is
(iv) Given
We can write as
We shall use the identity
Here
Hence the value of is
.
Q15.
Answer :
In the given problem, we have to find the value of
Given
We shall use the identity
Here putting,
Again squaring on both sides we get,
We shall use the identity
Again cubing on both sides we get,
We shall use identity
Hence the value of is
respectively.
Q16.
Answer :
In the given problem, we have to find the value of
Given
By adding and subtracting in left hand side of
we get,
Again by adding and subtracting in left hand side of
we get,
Now cubing on both sides of we get
we shall use identity
Hence the value of is
respectively.
Q17.
Answer :
In the given problem, we have to find the value of
(i) Given
On cubing both sides we get,
We shall use identity
Hence the value of is
(ii) Given
On cubing both sides we get,
We shall use identity
Hence the value of is
.
Q18.
Answer :
From given problem we have to find the value of
Given
On cubing both sides of we get
We shall use identity
Hence the value of is
.
Q19.
Answer :
In the given problem, we have to find the value of
Given
Cubing on both sides of we get
We shall use identity
Hence the value of is
.
Factorization Of Algebraic Expressions
Page no. 5.13 Ex. 5.2
Q1.
Answer :
The given expression to be factorized is
This can be written in the form
Recall the formula for sum of two cubes
Using the above formula, we have
We cannot further factorize the expression.
So, the required factorization of is
.
Q2.
Answer :
The given expression to be factorized is
This can be written in the form
Recall the formula for sum of two cubes
Using the above formula, we have
We cannot further factorize the expression.
So, the required factorization of is
.
Q3.
Answer :
The given expression to be factorized is
This can be written in the form
Recall the formula for difference of two cubes
Using the above formula, we have
We cannot further factorize the expression.
So, the required factorization of is
.
Q4.
Answer :
The given expression to be factorized is
This can be written in the form
Recall the formula for sum of two cubes
Using the above formula, we have
We cannot further factorize the expression.
So, the required factorization of is
.
Q5.
Answer :
The given expression to be factorized is
This can be written in the form
Recall the formula for difference of two cubes
Using the above formula, we have
We cannot further factorize the expression.
So, the required factorization of is
.
Q6.
Answer :
The given expression to be factorized is
This can be written in the form
Recall the formula for difference of two cubes
Using the above formula, we have
We cannot further factorize the expression.
So, the required factorization of is
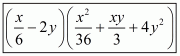
Q7.
Answer :
The given expression to be factorized is
Take common from the two terms,. Then we have
This can be written in the form
Recall the formula for difference of two cubes
Using the above formula, we have
We cannot further factorize the expression.
So, the required factorization of is
.
Q8.
Answer :
The given expression to be factorized is
Take common from the two terms,. Then we have
This can be written in the form
Recall the formula for sum of two cubes
Using the above formula, we have
We cannot further factorize the expression.
So, the required factorization of is
.
Q9.
Answer :
The given expression to be factorized is
Take common from the two terms,. Then we have
This can be written in the form
Recall the formula for sum of two cubes
Using the above formula, we have
We cannot further factorize the expression.
So, the required factorization of is
.
Page no. 5.14 Ex. 5.2
Q10.
Answer :
The given expression to be factorized is
This can be written in the form
Recall the formula for difference of two cubes
Using the above formula, we have
We cannot further factorize the expression.
So, the required factorization of is
.
Q11.
Answer :
The given expression to be factorized is
This can be written in the form
Recall the formula for difference of two cubes
Using the above formula, we have
We cannot further factorize the expression.
So, the required factorization of is
.
Q12.
Answer :
The given expression to be factorized is
Recall the formula for sum of two cubes
Using the above formula, we have
We cannot further factorize the expression.
So, the required factorization of is
.
Q13.
Answer :
The given expression to be factorized is
Take common. Then we have
This can be written as
Recall the formula for difference of two cubes
Using the above formula, we have
We cannot further factorize the expression.
So, the required factorization of is
.
Q14.
Answer :
The given expression to be factorized is
Take common 3. Then we have from the above expression,
This can be written as
Recall the formula for difference of two cubes
Using the above formula, we have
We cannot further factorize the expression.
So, the required factorization of is
.
Q15.
Answer :
The given expression to be factorized is
This can be written as
Recall the formula for sum of two cubes
Using the above formula, we have
We cannot further factorize the expression.
So, the required factorization of is
.
Q16.
Answer :
The given expression to be factorized is
This can be written as
Recall the formula for sum of two cubes
Using the above formula, we have
We cannot further factorize the expression.
So, the required factorization of is
.
Q17.
Answer :
The given expression to be factorized is
Take common. Then we have from the above expression,
This can be written as
Recall the formula for difference of two cubes
Using the above formula, we have
We cannot further factorize the expression.
So, the required factorization of is
.
Q18.
The given expression to be factorized is
This can be written as
Recall the formula for difference of two cubes
Using the above formula, we have
We cannot further factorize the expression.
So, the required factorization of is
.
Q19.
Answer :
The given expression to be factorized is
This can be written as
Take common x2 from first two terms, 2x from the next two terms andfrom the last two terms. Then we have,
Finally, take common. Then we get,
We cannot further factorize the expression.
So, the required factorization of is
.
Q20.
Answer :
The given expression to be factorized is
This can be written as
Recall the formula for sum of two cubes
Using the above formula, we have
Take common. Then we have
We cannot further factorize the expression.
So, the required factorization of is
.
Q21.
Answer :
The given expression to be factorized is
This can be written as
Recall the formula for sum of two cubes
Using the above formula and taking common from the last two terms, we get
Take common. Then we have,
We cannot further factorize the expression.
So, the required factorization of is
.
Q22.
Answer :
The given expression to be factorized is
Recall the well known formula
The given expression can be written as
Recall the formula for difference of two cubes
Using the above formula and taking common –2 from the last two terms, we get
We cannot further factorize the expression.
So, the required factorization of is
.
Q23.
Answer :
The given expression to be factorized is
The given expression can be written as
Recall the formula for difference of two cubes
Using the above formula and taking common from the last two terms, we get
Take common. Then we have,
We cannot further factorize the expression.
So, the required factorization of is
.
Q24.
Answer :
(i) The given expression is
Assumeand
. Then the given expression can be rewritten as
Recall the formula for sum of two cubes
Using the above formula, the expression becomes
Note that both and b are positive. So, neither
nor any factor of it can be zero.
Therefore we can cancel the termfrom both numerator and denominator. Then the expression becomes
(ii) The given expression is
Assumeand
. Then the given expression can be rewritten as
Recall the formula for difference of two cubes
Using the above formula, the expression becomes
Note that both, b is positive and unequal. So, neither
nor any factor of it can be zero.
Therefore we can cancel the termfrom both numerator and denominator. Then the expression becomes
(iii) The given expression is
Assumeand
. Then the given expression can be rewritten as
Recall the formula for difference of two cubes
Using the above formula, the expression becomes
Note that both, b is positive and unequal. So, neither
nor any factor of it can be zero.
Therefore we can cancel the termfrom both numerator and denominator. Then the expression becomes
Page no. 5.17 Ex. 5.3
Q1.
Answer :
The given expression to be factorized is
This can be written in the form
Take common from the last two terms,
This can be written in the following form
Recall the formula for the cube of the sum of two numbers
Using the above formula, we have
We cannot further factorize the expression.
So, the required factorization of is
.
Q2.
Answer :
The given expression to be factorized is
This can be written in the form
Take common from the last two terms,. Then we get
This can be written in the following form
Recall the formula for the cube of the difference of two numbers
Using the above formula, we have
We cannot further factorize the expression.
So, the required factorization is of is
.
Q3.
Answer :
The given expression to be factorized is
This can be written in the form
Take common from the last two terms,. Then we get
This can be written in the following form
Recall the formula for the cube of the sum of two numbers
Using the above formula, we have
We cannot further factorize the expression.
So, the required factorization is of is
.
Q4.
Answer :
The given expression to be factorized is
This can be written in the form
Take common from the last two terms. Then we get
This can be written in the following form
Recall the formula for the cube of the sum of two numbers
Using the above formula, we have
We cannot further factorize the expression.
So, the required factorization is of is
.
Q5.
Answer :
The given expression to be factorized is
This can be written in the form
Take common from the third and fourth terms. Then we get
This can be written in the following form
Recall the formula for the cube of the difference of two numbers
Using the above formula, we have
This can be written in the following form
Recall the formula for the sum of two cubes
Using the above formula, we have
We cannot further factorize the expression.
So, the required factorization is ofis
Q6.
Answer :
The given expression to be factorized is
This can be written in the form
Take common from the last two terms. Then we get
This can be written in the following form
Recall the formula for the cube of the sum of two numbers
Using the above formula, we have
We cannot further factorize the expression.
So, the required factorization is of is
.
Q7.
Answer :
The given expression to be factorized is
This can be written in the form
Take common 6xy from the last two terms,. Then we get
This can be written in the following form
Recall the formula for the cube of the sum of two numbers
Using the above formula, we have
We cannot further factorize the expression.
So, the required factorization is of is
.
Q8.
Answer :
The given expression to be factorized is
This can be written in the form
Take common from the last two terms,. Then we get
This can be written in the following form
Recall the formula for the cube of the sum of two numbers
Using the above formula, we have
We cannot further factorize the expression.
So, the required factorization is of is
.
Q9.
Answer :
The given expression to be factorized is
This can be written in the form
Take common – 18ab from the last two terms,. Then we get
This can be written in the following form
Recall the formula for the cube of the difference of two numbers
Using the above formula, we have
We cannot further factorize the expression.
So, the required factorization is ofis
.
Q10.
Answer :
The given expression to be factorized is
This can be written in the form
Take common – 12x from the last two terms,. Then we get
This can be written in the following form
Recall the formula for the cube of the difference of two numbers
Using the above formula, we have
We cannot further factorize the expression.
So, the required factorization is of is
.
Q11.
Answer :
The given expression to be factorized is
This can be written in the form
Take common from the last two terms,. Then we get
This can be written in the following form
Recall the formula for the cube of the difference of two numbers
Using the above formula, we have
We cannot further factorize the expression.
So, the required factorization is of is
.
Page no. 5.22 Ex. 5.4
Q1.
Answer :
The given expression to be factorized is
This can be written in the form
Recall the formula
Using the above formula, we have
We cannot further factorize the expression.
So, the required factorization of is
Q2.
Answer :
The given expression to be factorized is
This can be written in the form
Recall the formula
Using the above formula, we have
We cannot further factorize the expression.
So, the required factorization is ofis
Q3.
Answer :
The given expression to be factorized is
This can be written in the form
Recall the formula
Using the above formula, we have
We cannot further factorize the expression.
So, the required factorization is of is
Q4.
Answer :
The given expression to be factorized is
This can be written in the form
Recall the formula
Using the above formula, we have
We cannot further factorize the expression.
So, the required factorization is ofis
Q5.
Answer :
The given expression to be factorized is
This can be written in the form
Recall the formula
Using the above formula, we have
We cannot further factorize the expression.
So, the required factorization is ofis
Q6.
Answer :
The given expression to be factorized is
This can be written in the form
Recall the formula
Using the above formula, we have
We cannot further factorize the expression.
So, the required factorization is ofis
Q7.
Answer :
The given expression to be factorized is
Let,
and
. Then the given expression becomes
Note that
Recall the formula
When, this becomes
So, we have the new formula
,
when.
Using the above formula, the given expression can be written as
Put,
and
. Then we have
We cannot further factorize the expression.
So, the required factorization is ofis
Q8.
Answer :
The given expression to be factorized is
Let,
and
. Then the given expression becomes
Note that
Recall the formula
When, this becomes
So, we have the new formula
, when
.
Using the above formula, the given expression can be written as
Put,
and
. Then we have
We cannot further factorize the expression.
So, the required factorization is ofis
Q9.
Answer :
The given expression to be factorized is
Let,
and
. Then the given expression becomes
Note that
Recall the formula
When, this becomes
So, we have the new formula
, when
.
Using the above formula, the given expression can be written as
Put,
and
.
Then we have
We cannot further factorize the expression.
So, the required factorization is of is
Q10.
Answer :
The given expression to be factorized is
Let,
and
. Then the given expression becomes
Note that
Recall the formula
When, this becomes
So, we have the new formula
, when
.
Using the above formula, the given expression can be written as
Put,
and
. Then we have
We cannot further factorize the expression.
So, the required factorization is ofis
Q11.
Answer :
The given expression to be factorized is
This can be written in the form
Recall the formula
Using the above formula, we have
We cannot further factorize the expression.
So, the required factorization is of is
.
Page no. 5.23 Ex. 5.4
Q12.
Answer :
The given expression to be factorized is
This can be written in the form
Recall the formula
Using the above formula, we have
We cannot further factorize the expression.
So, the required factorization is of is
Q13.
Answer :
The given expression to be factorized is
This can be written in the form
Recall the formula
Using the above formula, we have
We cannot further factorize the expression.
So, the required factorization is ofis
.
Q14.
Answer :
The given expression to be factorized is
This can be written in the form
Recall the formula
Using the above formula, we have
We cannot further factorize the expression.
So, the required factorization is of is
Q15.
Answer :
The given expression is
It is given that
The given expression can be written in the form
Recall the formula
Using the above formula, we have
Q16.
Answer :
(i) The given expression is
We have to multiply the above expression by.
The required product is
Recall the formula
Using the above formula, we have
(ii) The given expression is
We have to multiply the above expression by.
The required product is
Recall the formula
Using the above formula, we have
(iii) The given expression is
We have to multiply the above expression by.
The required product is
Recall the formula
Using the above formula, we have
(iii) The given expression is
We have to multiply the above expression by.
The required product is
Recall the formula
Using the above formula, we have
Page no. 5.24 Formative Assessment_VSA
Q1.
Answer :
The given expression to be factorized is
This can be written in the form
We cannot further factorize the expression.
So, the required factorization is.
Q2.
Answer :
The given expression to be factorized is
Take commonfrom the last three terms and then we have
We cannot further factorize the expression.
So, the required factorization is.
Q3.
Answer :
Recall the formula
When, we have
Q4.
Answer :
Recall the formula
Given that
Then we have
Q5.
Answer :
Recall the formula
Given that
,
Then we have
Q6.
Answer :
Recall the formula
Given that
,
Then we have
Q7.
Answer :
The given expression is
Let,
and
. Then the given expression becomes
Note that
Recall the formula
When, this becomes
So, we have the new formula
, when
.
Using the above formula, the value of the given expression is
Q8.
Answer :
The given expression is
Let,
and
. Then the given expression becomes
Note that
Recall the formula
When, this becomes
So, we have the new formula
, when
.
Using the above formula, the value of the given expression is
Q9.
Answer :
The given expression is
Let,
and
. Then the given expression becomes
Note that:
Recall the formula
When, this becomes
So, we have the new formula
, when
.
Using the above formula, the value of the given expression is
Q10.
Answer :
The given expression is
Let,
and
. Then the given expression becomes
Note that
Recall the formula
When, this becomes
So, we have the new formula
, when
.
Using the above formula, the value of the given expression is
Page no. 5.24 Formative Assessment_MCQ
Q1.
Answer :
The given expression to be factorized is
Take commonfrom the last three terms and then we have
So, the correct choice is (c).
Q2.
Answer :
The given expression to be factorized is
This can be written in the form
So, the correct choice is (a).
Q3.
Answer :
The given expression to be factorized is
This can be arrange in the form
Let. Then the above expression becomes
Put.
So, the correct choice is (a).
Q4.
Answer :
The given expression to be factorized is
Take common from the first two terms and
from the last two terms. That is
Finally, take commonfrom the two terms. That is
So, the correct choice is (d).
Page no. 5.25 Formative Assessment_MCQ
Q5.
Answer :
The given expression to be factorized is
This can be written in the form
Recall the formula
Using the above formula, we have
So, the correct choice is (a).
Q6.
Answer :
The given expression to be factorized is
This can be written in the form
Recall the formula
Using the above formula, we have
So, the correct choice is (c).
Q7.
Answer :
The given expression to be factorized is
Recall the formula for difference of two cubes
Using the above formula, we have,
So, the correct choice is (a).
Q8.
Answer :
The given expression to be factorized is
This can be written in the form
Take common x from the first two terms andfrom the last two terms. Then we have
Finally, take commonfrom the above expression,
So, the correct choice is (d).
Q9.
Answer :
The given expression is
Let,
and
. Then the given expression becomes
![]()
Note that:
Recall the formula
When, this becomes
So, we have the new formula
, when
.
Using the above formula, the value of the given expression is
So, the correct choice is (b).
Q10.
The given expression to be factorized is
This can be written in the form
So, the correct choice is (a).
Q11.
Answer :
The given expression is
Recall the formula
Using the above formula the given expression becomes
Given that
Therefore the value of the given expression is
So, the correct choice is (c).
Q12.
Answer :
The given equation is
Recall the formula
Using the above formula, we have
, provided
.
So, the correct choice is (d).
Q13.
Answer :
The given equation is
This can be written as
Comparing the coefficients on both sides of the equation.
We get,
Putting the value of a from (1) in (2)
We get,
So the value of a, b and c is 1, – 4 and 7 respectively.
Therefore,
a + b + c =1-4 + 7 = 4
So, the correct choice is (a).
Q14.
Answer :
The given expression is
This can be written in the form
Assumeand
. Then the given expression can be rewritten as
Recall the formula for difference of two cubes
Using the above formula, the expression becomes
Note that both a and b are positive, unequal. So, neithernor any factor of it can be zero.
Therefore we can cancel the termfrom both numerator and denominator. Then the expression becomes
So, the correct choice is (a).
Page no. 5.25 Formative Assessment_MCQ
Q15.
Answer :
The given expression is
Assumeand
. Then the given expression can be rewritten as
Recall the formula for sum of two cubes
Using the above formula, the expression becomes
Note that both and b are positive. So, neither
nor any factor of it can be zero.
Therefore we can cancel the termfrom both numerator and denominator. Then the expression becomes
So, the correct choice is (b).
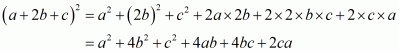
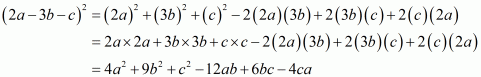
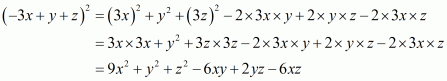
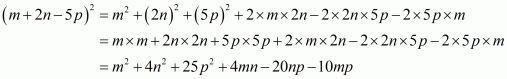
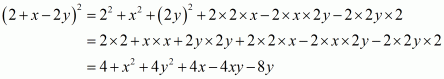
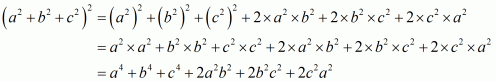
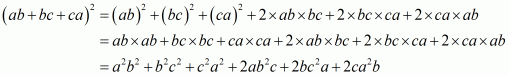
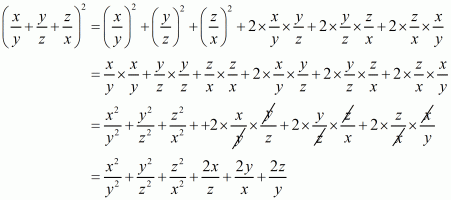
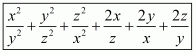
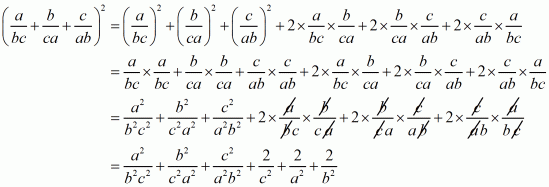
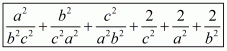
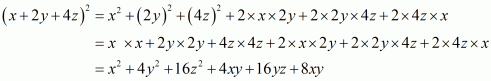
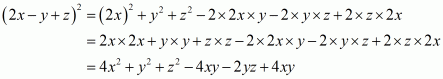
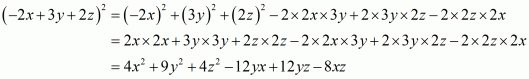
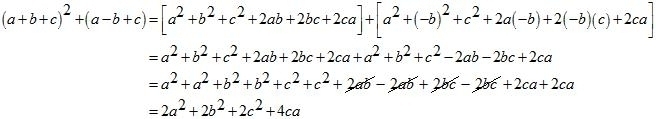
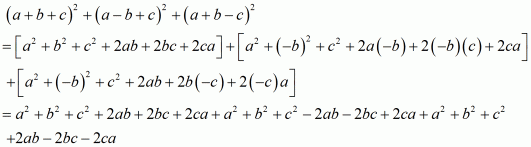
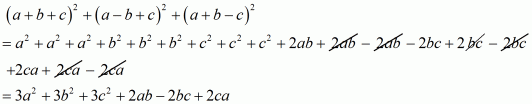
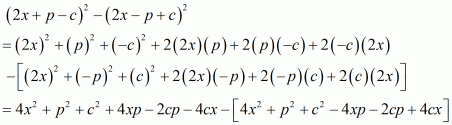
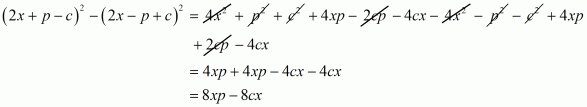
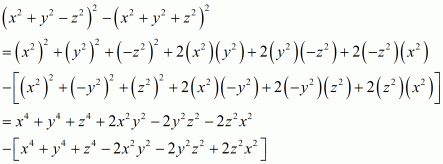
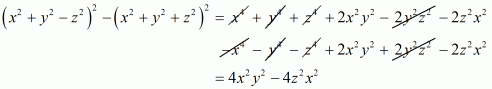
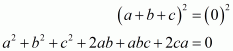
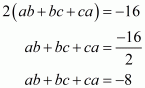
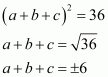
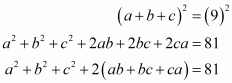
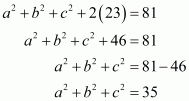
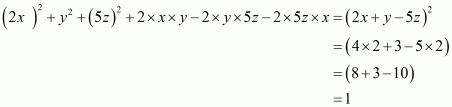
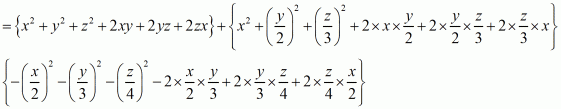
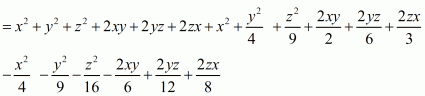
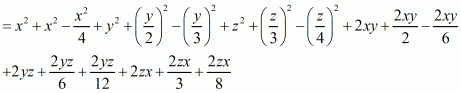
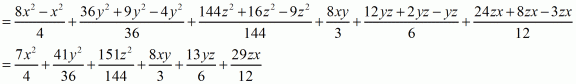
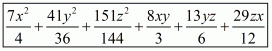
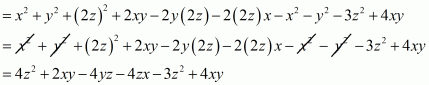
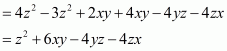
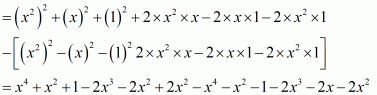
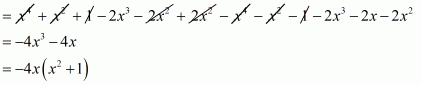
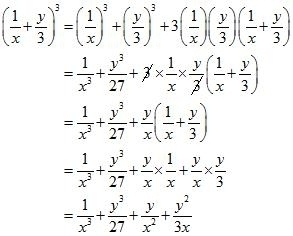
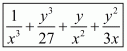
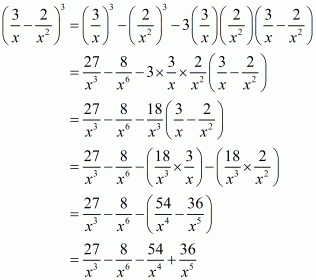
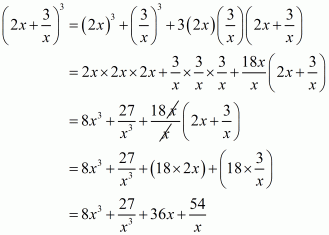
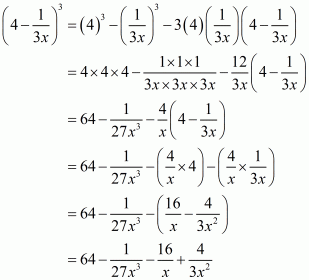
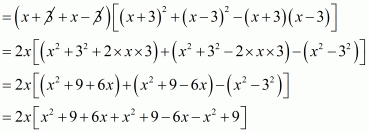
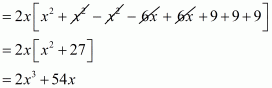
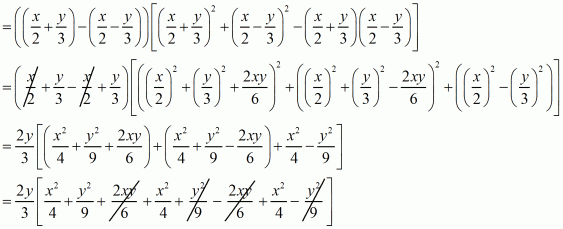
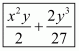
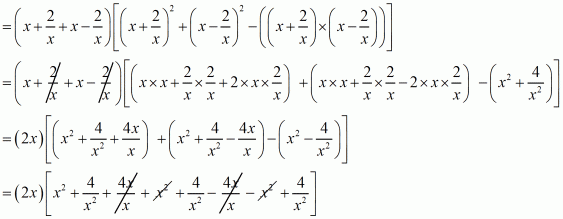
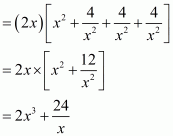
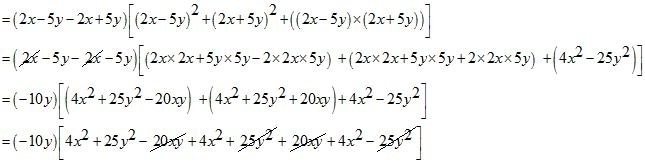
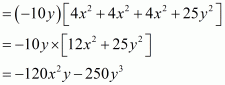
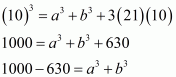
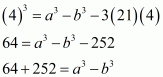
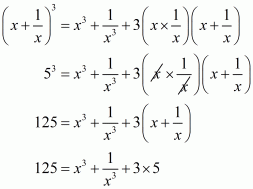
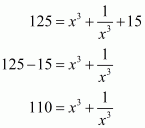
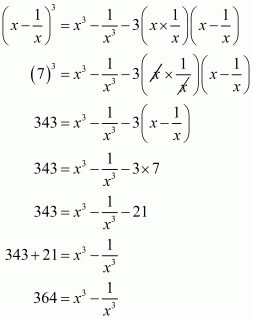
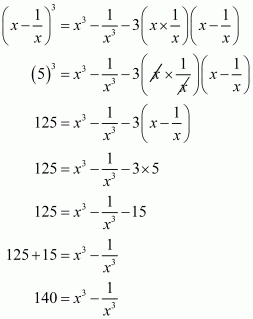
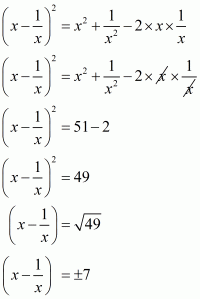
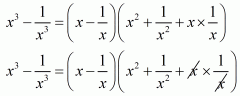
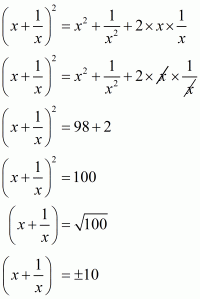
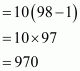
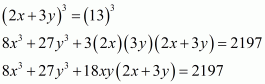
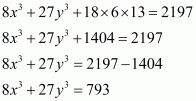
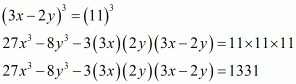
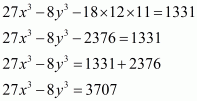
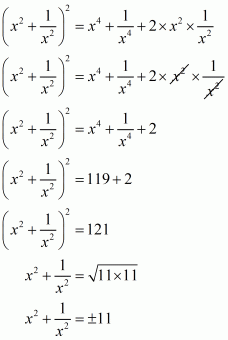
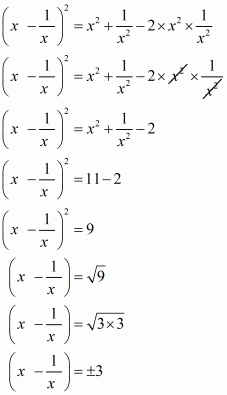
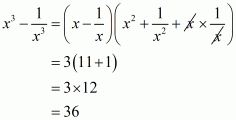
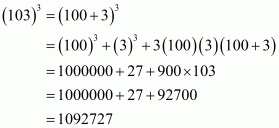
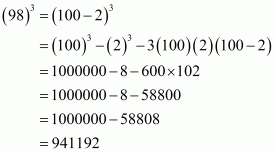
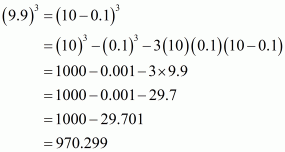
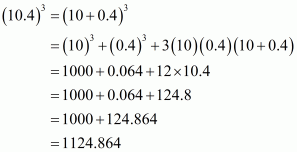
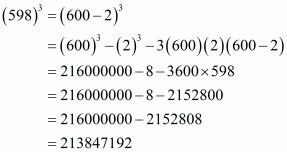
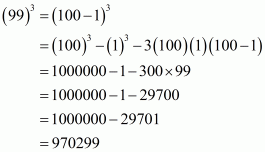
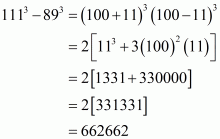
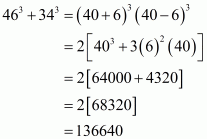
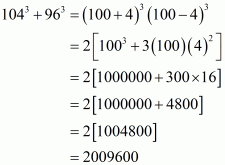
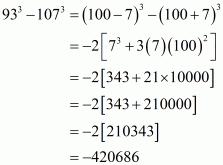
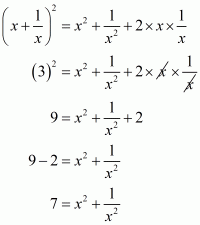
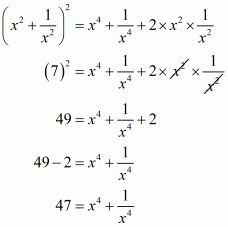
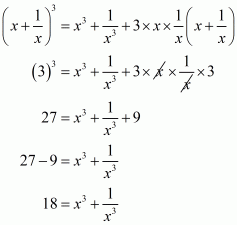
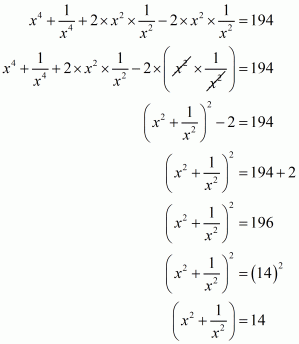
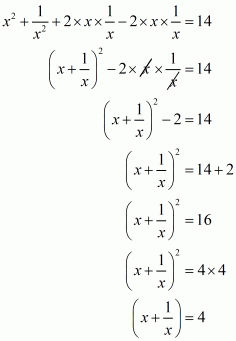
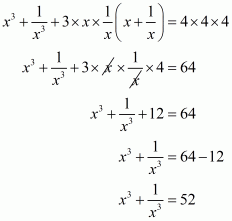
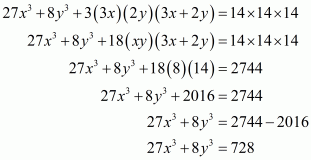
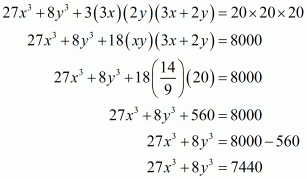
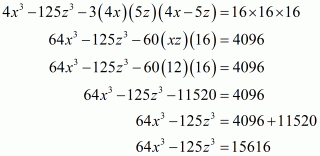
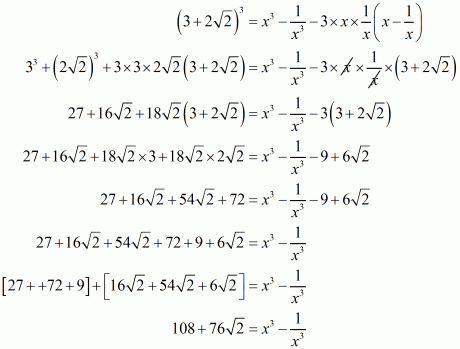
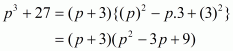
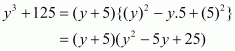
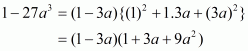
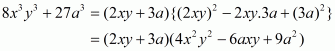
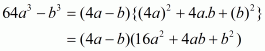
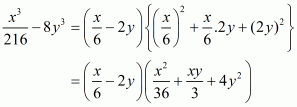
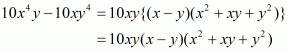
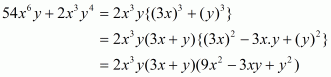
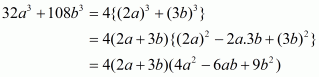
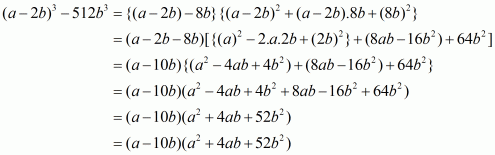
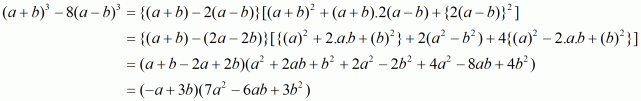
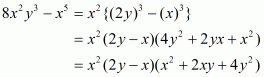
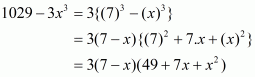
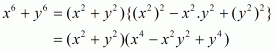
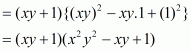
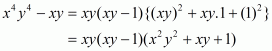
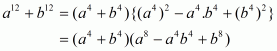
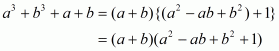
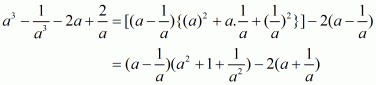
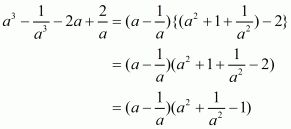
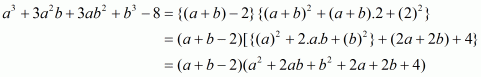
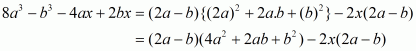
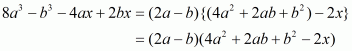
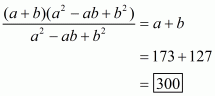
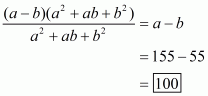
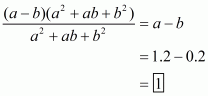
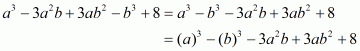
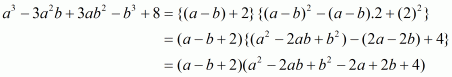
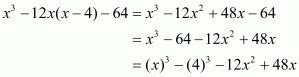
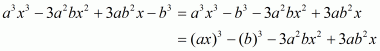
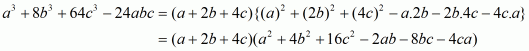
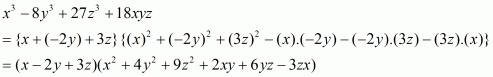
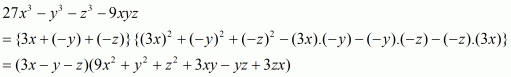
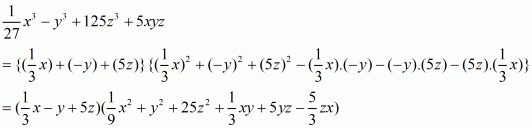
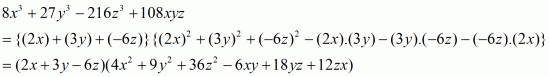
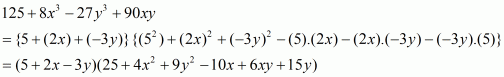
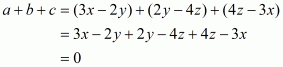
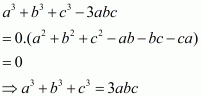
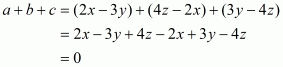
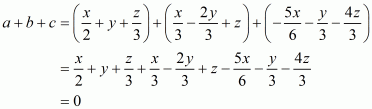
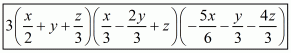
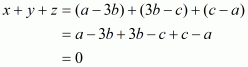
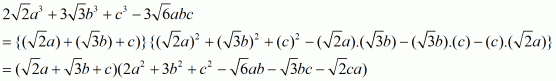
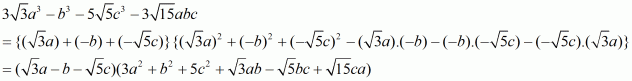
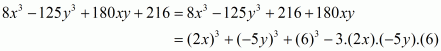
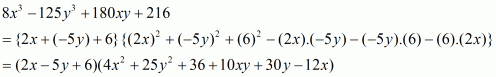
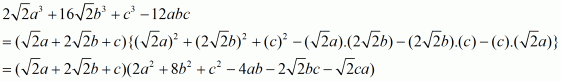
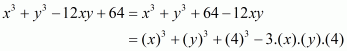
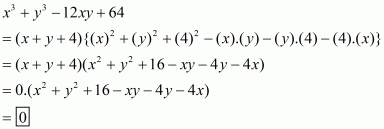
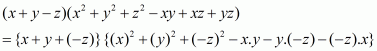
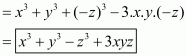
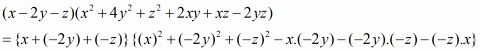
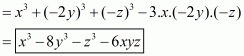
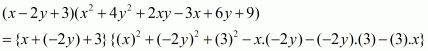
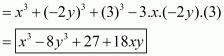
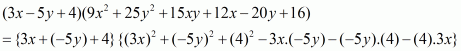
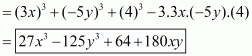
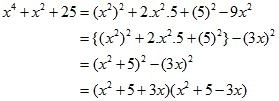
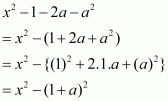
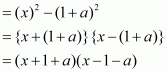
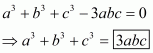
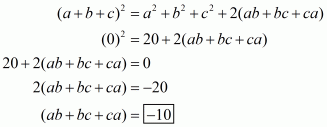
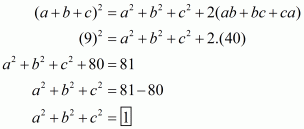
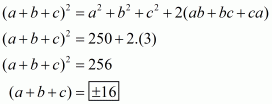
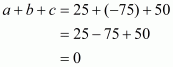
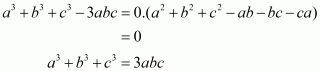
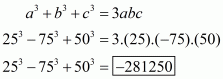
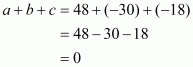
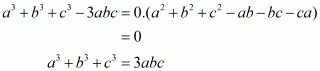
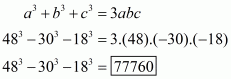
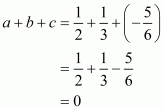
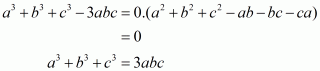
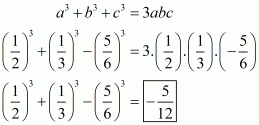
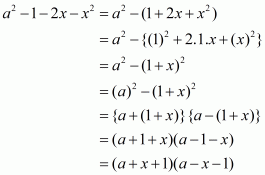
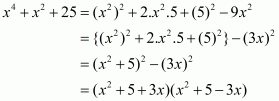
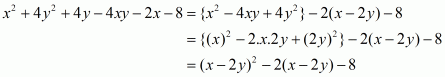
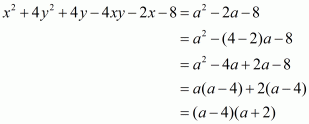
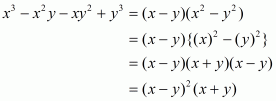
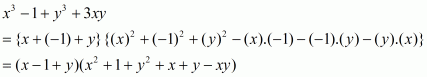
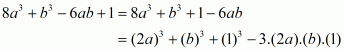
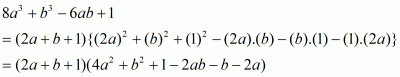
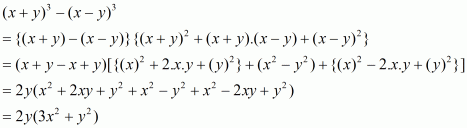
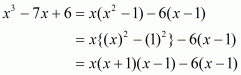
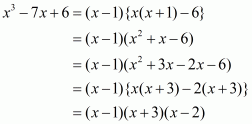
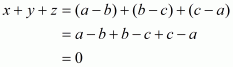
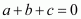
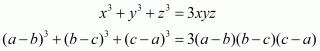
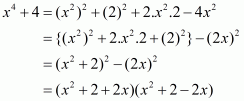
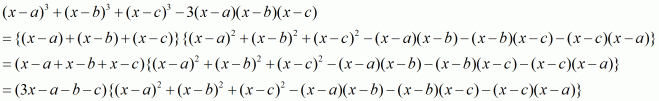
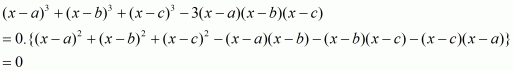
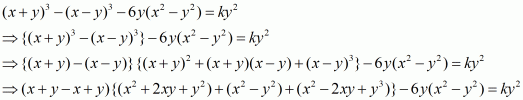
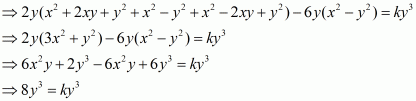
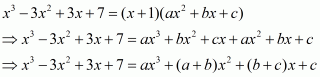
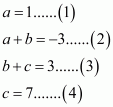
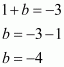
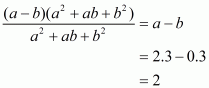
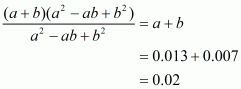

Leave a Reply