Page 14.4 Ex. 14.1
Q1.
Answer :
Let the measure of the fourth angles be x°. We know that the sum of the angles of a quadrilateral is 360°.
Therefore,
Hence the measure of the fourth angle is .
Q2.
Answer :
We have ,.
So, let ,
,
And
By angle sum property of a quadrilateral, we get:
Also,
And
Similarly,
Hence, the four angles are ,
,
and
.
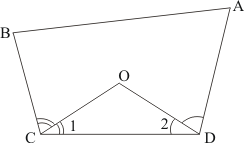
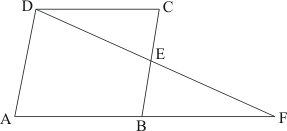
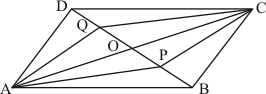
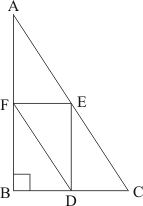
Q3.
Answer :
The quadrilateral can be drawn as follows:
We have CO and DO as the bisectors of angles and
respectively.
We need to prove that.
In ,We have,
…… (I)
By angle sum property of a quadrilateral, we have:
Putting in equation (I):
Hence proved.
Q4.
Answer :
We have, .
So, let ,
,
and
By angle sum property of a quadrilateral, we get:
Also,
And
Similarly,
Hence, the four angles are ,
,
and
.
Page 14.18 Ex. 14.2
Q1.
Answer :
It is given that the two opposite angles of a parallelogram are and
.
We know that the opposite angles of a parallelogram are equal.
Therefore,
…… (i)
Thus, the given angles become
Also, .
Therefore the sum of consecutive interior angles must be supplementary.
That is;
Since opposite angles of a parallelogram are equal.
Therefore,
And
Hence the four angles of the parallelogram are ,
,
and
.
Q2.
Answer :
Let one of the angle of the parallelogram as
Then the adjacent angle becomes
We know that the sum of adjacent angles of the parallelogram is supplementary.
Therefore,
Thus, the angle adjacent to
Since, opposite angles of a parallelogram are equal.
Therefore, the four angles in sequence are ,
,
and
.
Q3.
Answer :
Let the smallest angle of the parallelogram be
Therefore, according to the given statement other angle becomes .
Also, the opposite angles of a parallelogram are equal.
Therefore, the four angles become ,
,
and
.
According to the angle sum property of a quadrilateral:
Thus, the other angle becomes
Hence, the four angles of the parallelogram are ,
,
and
.
Q4.
Answer :
Let the shorter side of the parallelogram be cm.
The longer side is given ascm.
Perimeter of the parallelogram is given as 22 cm
Therefore,
Hence, the measure of the shorter side is cm.
Q5.
Answer :
It is given that ABCD is a parallelogram with
We know that the opposite angles of the parallelogram are equal.
Therefore,
Also, and
are adjacent angles, which must be supplementary.
Therefore,
Hence , and
.
Q6.
Answer :
It is given that ABCD is a parallelogram with
We know that the opposite angles of the parallelogram are equal.
Therefore,
Also, and
are adjacent angles, which must be supplementary.
Therefore,
Also, and
are opposite angles of a parallelogram.
Therefore,
Hence, the angles of a parallelogram are ,
,
and
.
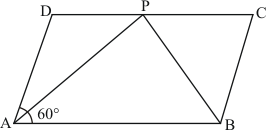
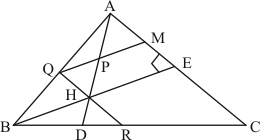
Q7.
Answer :
The figure is given as follows:
It is given that ABCD is a parallelogram.
Thus,
Opposite angles of a parallelogram are equal.
Therefore,
Also, we have AP as the bisector of
Therefore,
…… (i)
Similarly,
…… (ii)
We have ,
From (i)
Thus, sides opposite to equal angles are equal.
Similarly,
From (ii)
Thus, sides opposite to equal angles are equal.
Also,
Q8.
Answer :
The figure is given as follows:
It is given that ABCD is a parallelogram.
Thus
And are
alternate interior opposite angles.
Therefore,
…… (i)
We know that the opposite angles of a parallelogram are equal. Therefore,
Also, we have
Therefore,
…… (ii)
In
By angle sum property of a triangle.
From (i) and (ii),we get:
Hence, the required value for is
And is
.
Page 14.19 Ex. 14.2
Q9.
Answer :
Figure is given as follows:
It is given that ABCD is a parallelogram.
DE and AB when produced meet at F.
We need to prove that
It is given that
Thus, the alternate interior opposite angles must be equal.
In and
, we have
(Proved above)
(Given)
(Vertically opposite angles)
Therefore,
(By ASA Congruency )
By corresponding parts of congruent triangles property, we get
DC = BF …… (i)
It is given that ABCD is a parallelogram. Thus, the opposite sides should be equal. Therefore,
…… (ii)
But,
From (i), we get:
From (ii), we get:
Hence proved.
Q10.
Answer :
(i) Statement: In a parallelogram, the diagonals are equal.
False
(ii) Statement: In a parallelogram, the diagonals bisect each other.
True
(iii) Statement: In a parallelogram, the diagonals intersect each other at right angles.
False
(iv) Statement: In any quadrilateral, if a pair of opposite sides is equal, it is a parallelogram.
False
(v) Statement: If all the angles of a quadrilateral are equal, then it is a parallelogram.
True
(vi) Statement: If three sides of a quadrilateral are equal, then it is not necessarily a parallelogram.
False
(vii) Statement: If three angles of a quadrilateral are equal, then it is no necessarily a parallelogram.
False
(viii) Statement: If all sides of a quadrilateral are equal, then it is a parallelogram.
True
Page 14.38 Ex. 14.3
Q1.
Answer :
The parallelogram can be drawn as:
We have ,thus
and
are consecutive interior angles.
These must be supplementary.
Therefore,
Q2.
Answer :
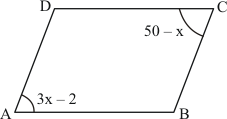
Since ABCD is a parallelogram with .
Opposite angles of a parallelogram are equal.
Therefore,
Also, let
Similarly,
We know that the sum of the angles of a quadrilateral is .
Hence the measure of other angles are ,
and
.
Q3.
Answer :
The figure can be drawn as follows:
In and
,
(Sides of a square are equal)
(Diagonals of a parallelogram bisect each other)
(Common)
So, by SSS Congruence rule, we have
Also,
(Corresponding parts of congruent triangles are equal)
But, (Linear pairs)
We have,
Hence, the required measure of is
.
Q4.
Answer :
The rectangle is given as follows with
We have to find .
An angle of a rectangle is equal to .
Therefore,
Hence, the measure for is
.
Q5.
Answer :
Figure is given as follows:
It is given that ABCD is a parallelogram.
E is the mid point of AB
Thus,
,
…… (i)
Similarly,
……(ii)
From (i) and (ii)
Also,
Thus,
Therefore, EBFD is a parallelogram.
Q6.
Answer :
Figure can be drawn as follows:
We have P and Q as the points of trisection of the diagonal BD of parallelogram ABCD.
We need to prove that AC bisects PQ. That is, .
Since diagonals of a parallelogram bisect each other.
Therefore, we get:
and
P and Q as the points of trisection of the diagonal BD.
Therefore,
and
Now, and
Thus,
Hence proved.
Q7.
Answer :
Square ABCD is given:
E, F, G and H are the points on AB, BC, CD and DA respectively, such that :
We need to prove that EFGH is a square.
Say,
As sides of a square are equal. Then, we can also say that:
In and
,we have:
(Given)
(Each equal to 90°)
(Each equal to y )
By SAS Congruence criteria, we have:
Therefore, EH = EF
Similarly, EF= FG, FG= HG and HG= HE
Thus, HE=EF=FG=HG
Also,
and
But,
and
Therefore,
i.e.,
Similarly,
Thus, EFGH is a square.
Hence proved.
Q8.
Answer :
Rhombus ABCD is given:
We have
We need to prove that
We know that the diagonals of a rhombus bisect each other at right angle.
Therefore,
,
,
In A and O are the mid-points of BE and BD respectively.
By using mid-point theorem, we get:
Therefore,
In A and O are the mid-points of BE and BD respectively.
By using mid-point theorem, we get:
Therefore,
Thus, in quadrilateral DOCG,we have:
and
Therefore, DOCG is a parallelogram.
Thus, opposite angles of a parallelogram should be equal.
Also, it is given that
Therefore,
Or,
Hence proved.
Q9.
Answer :
ABCD is a parallelogram, AD produced to E such that .
Also , AB produced to F.
We need to prove that
In , D and O are the mid-points of AE and AC respectively.
By using Mid-point Theorem, we get:
Since, BD is a straight line and O lies on AC.
And, C lies on EF
Therefore,
…… (i)
Also, is a parallelogram with
.
Thus,
In and
,we have:
So, by ASA Congruence criterion, we have:
By corresponding parts of congruence triangles property, we get:
Hence proved.
Page 14.55 Ex. 14.4
Q1.
Answer :
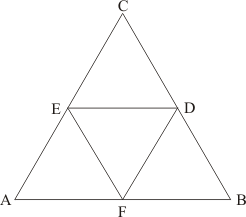
is given with D,E and F as the mid-points of BC , CA and AB respectively as shown below:
Also, ,
and
.
We need to find the perimeter of
In , E and F are the mid-points of CA and AB respectively.
Theorem states, the line segment joining the mid-points of any two sides of a triangle is parallel to the third side and equal to half of it.
Therefore, we get:
Similarly, we get
And
Perimeter of
Hence, the perimeter of is
.
Q2.
Answer :
It is given that D, E and F be the mid-points of BC , CA and AB respectively.
Then,
,
and
.
Now, and transversal CB and CA intersect them at D and E respectively.
Therefore,
[
(Given)]
and
[
(Given)]
Similarly,
Therefore,
[
(Given)]
and
[
(Given)]
Similarly,
Therefore,
[
(Given)] and
[
(Given)]
Now BC is a straight line.
Similarly,
and
Hence the measure of angles are ,
and
.
Q3.
Answer :
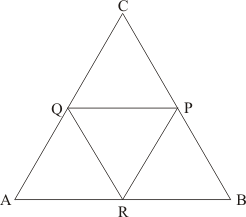
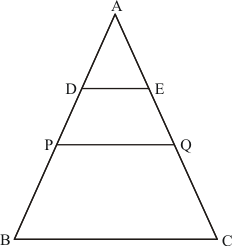
It is given that P, Q and R are the mid-points of BC, CA and AB respectively.
Also, we have ,
and
We need to find the perimeter of quadrilateral ARPQ
In , P and R are the mid-points of CB and AB respectively.
Theorem states, the line segment joining the mid-points of any two sides of a traingle is parallel to the third side and equal to half of it.
Therefore, we get:
Similarly, we get
We have Q and R as the mid points of AC and AB respectively.
Therefore,
And
Perimeter of
Hence, the perimeter of quadrilateral ARPQ is.
Q4.
Answer :
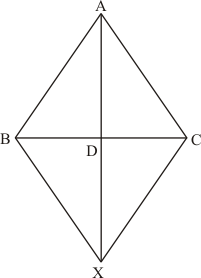
is given with AD as the median extended to point X such that
.
Join BX and CX.
We get a quadrilateral ABXC, we need to prove that it’s a parallelogram.
We know that AD is the median.
By definition of median we get:
Also, it is given that
Thus, the diagonals of the quadrilateral ABCX bisect each other.
Therefore, quadrilateral ABXC is a parallelogram.
Hence proved.
Q5.
Answer :
is given with E and F as the mid points of sides AB and AC.
Also, intersecting EF at Q.
We need to prove that
In , E and F are the mid-points of AB and AC respectively.
Theorem states, the line segment joining the mid-points of any two sides of a triangle is parallel to the third side and equal to half of it.
Therefore, we get:
Since, Q lies on EF.
Therefore,
This means,
Q is the mid-point of AP.
Thus, (Because, F is the mid point of AC and
)
Hence proved.
Q6.
Answer :
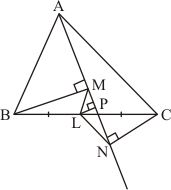
In , BM and CN are perpendiculars on any line passing through A.
Also.
We need to prove that
From point L let us draw
It is given that ,
and
Therefore,
Since, L is the mid points of BC,
Therefore intercepts made by these parallel lines on MN will also be equal
Thus,
Now in ,
And . Thus, perpendicular bisects the opposite sides.
Therefore, is isosceles.
Hence
Hence proved.
Q7.
Answer :
We have right angled at B.
It is given that and
D and E are the mid-points of sides AB and AC respectively.
(i) We need to calculate length of BC.
In right angled at B:
By Pythagoras theorem,
Hence the length of BC is .
(ii) We need to calculate area of .
In right angled at B, D and E are the mid-points of AB and AC respectively.
Theorem states, the line segment joining the mid-points of any two sides of a triangle is parallel to the third side and equal to half of it.
Therefore, .
Thus, (Corresponding angles of parallel lines are equal)
And
area of
D is the mid-point of side AB .
Therefore, area of
Hence the area of is
.
Q8.
Answer :
We have as follows:
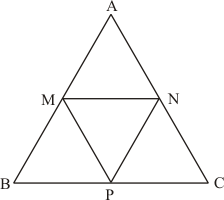
M, N and P are the mid-points of sides AB ,AC and BC respectively.
Also, ,
and
We need to calculate BC, AB and AC.
In , M and N are the mid-points of AB and AC respectively.
Theorem states, the line segment joining the mid-points of any two sides of a triangle is parallel to the third side and equal to half of it.
Therefore,
Similarly,
And
Hence, the measure for BC, AB and AC is ,
and
respectively.
Page 14.56 Ex. 14.4
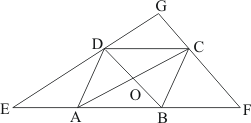
Q9.
Answer :
We have as follows:
Through A,B and C lines are drawn parallel to BC,CA and AB respectively intersecting at P,Q and R respectively.
We need to prove that perimeter of is double the perimeter of
.
and
Therefore, is a parallelogram.
Thus,
Similarly,
is a parallelogram.
Thus,
Therefore,
Then, we can say that A is the mid-point of QR.
Similarly, we can say that B and C are the mid-point of PR and PQ respectively.
In ,
Theorem states, the line drawn through the mid-point of any one side of a triangle is parallel to the another side, intersects the third side at its mid-point.
Therefore,
Similarly,
Perimeter of is double the perimeter of
Hence proved.
Q10.
Answer :
is given with
AD is any line from A to BC intersecting BE in H.
P,Q and R respectively are the mid-points of AH,AB and BC.
We need to prove that
Let us extend QP to meet AC at M.
In , R and Q are the mid-points of BC and AB respectively.
Theorem states, the line segment joining the mid-points of any two sides of a triangle is parallel to the third side and equal to half of it.
Therefore, we get:
…… (i)
Similarly, in,
…… (ii)
From (i) and (ii),we get:
and
We get, is a parallelogram.
Also,
Therefore, is a rectangle.
Thus,
Or,
Hence proved.
Q11.
Answer :
We have the following given figure:
We have and
and AP is the bisector of exterior angle
of
.
(i) We need to prove that
In ,
We have (Given)
Thus, (Angles opposite to equal sides are equal)
By angle sum property of a triangle, we get:
…… (i)
Now,
(AP is the bisector of exterior angle
)
(Linear Pair)
…… (ii)
From equation (i) and (ii),we get:
(ii) We need to prove that is a parallelogram.
We have proved that
This means,
Also it is given that
We know that a quadrilateral with opposite sides parallel is a parallelogram.
Therefore, is a parallelogram.
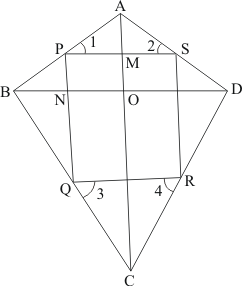
Q12.
Answer :
ABCD is a kite such that and
Quadrilateral PQRS is formed by joining the mid-points P,Q,R and S of sides AB,BC,CD and AD respectively.
We need to prove that Quadrilateral PQRS is a rectangle.
In , P and Q are the mid-points of AB and BC respectively.
Therefore,
and
Similarly, we have
and
Thus,
and
Therefore, PQRS is a parallelogram.
Now,
But, P and S are the mid-points of AB and AD
…… (I)
In : P and S are the mid-point of side AB and AD
By mid-point Theorem, we get:
Or,
In , P is the mid-point of side AB and
By Using the converse of mid-point theorem, we get:
M is the mid-point of AO
Thus,
…… (II)
In and have:
(Common)
[From (I)]
[From (II)]
By SSS Congruence theorem, we get:
By corresponding parts of congruent triangles property, we get:
But,
and
Therefore,
(
, Corresponding angles should be equal)
Or,
We have proved that
Similarly, .
Then we can say that and
Therefore, is a parallelogram with
Or, we can say that is a rectangle.
We get:
Also, PQRS is a parallelogram.
Therefore, PQRS is a rectangle.
Hence proved.
Q13.
Answer :
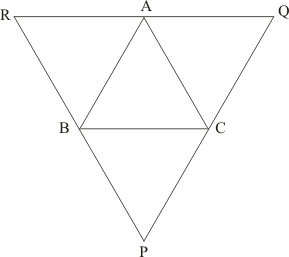
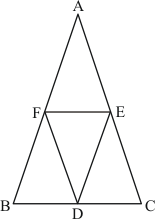
, an isosceles triangle is given with D,E and F as the mid-points of BC, CA and AB respectively as shown below:
We need to prove that the segment AD and EF bisect each other at right angle.
Let’s join DF and DE.
In , D and E are the mid-points of BC and AC respectively.
Theorem states, the line segment joining the mid-points of any two sides of a triangle is parallel to the third side and equal to half of it.
Therefore, we get: Or
Similarly, we can get
Therefore, AEDF is a parallelogram
We know that opposite sides of a parallelogram are equal.
and
Also, from the theorem above we get
Thus,
Similarly,
It is given that , an isosceles triangle
Thus,
Therefore,
Also,
Then, AEDF is a rhombus.
We know that the diagonals of a rhombus bisect each other at right angle.
Therefore, M is the mid-point of EF and
Hence proved.
Q14.
Answer :
is given with D a point on AB such that
.
Also, E is point on AC such that.
We need to prove that
Let P and Q be the mid points of AB and AC respectively.
It is given that
and
But, we have taken P and Q as the mid points of AB and AC respectively.
Therefore, D and E are the mid-points of AP and AQ respectively.
In , P and Q are the mid-points of AB and AC respectively.
Theorem states, the line segment joining the mid-points of any two sides of a triangle is parallel to the third side and equal to half of it.
Therefore, we get and
…… (i)
In , D and E are the mid-points of AP and AQ respectively.
Therefore, we get and
…… (ii)
From (i) and (ii),we get:
Hence proved.
Q15.
Answer :
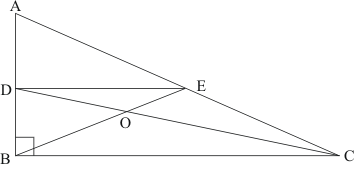
Figure is given as follows:
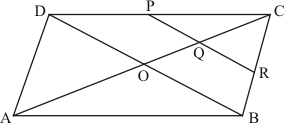
ABCD is a parallelogram, where P is the mid-point of DC and Q is a point on AC such that
.
PQ produced meets BC at R.
We need to prove that R is a mid-point of BC.
Let us join BD to meet AC at O.
It is given that ABCD is a parallelogram.
Therefore, (Because diagonals of a parallelogram bisect each other)
Also,
Therefore,
In , P and Q are the mid-points of CD and OC respectively.
Theorem states, the line segment joining the mid-points of any two sides of a triangle is parallel to the third side and equal to half of it.
Therefore, we get:
Also, in , Q is the mid-point of OC and
Therefore, R is a mid-point of BC.
Hence proved.
Q16.
Answer :
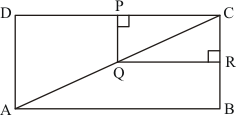
Rectangles ABCD and PQRC are given as follows:
Q is the mid-point of AC.
In , Q is the mid-point of AC such that
Using the converse of mid-point theorem, we get:
P is the mid-point of DC
That is;
Similarly, R is the mid-point of BC.
Now, in , P and R are the mid-points of DC and BC respectively.
Then, by mid-point theorem, we get:
Now, diagonals of a rectangle are equal.
Therefore putting ,we get:
Hence Proved.
Q17.
Answer :
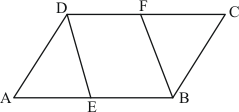
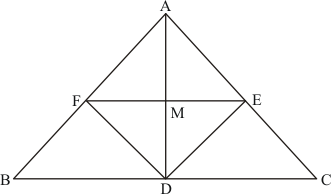
ABCD is a parallelogram with E and F as the mid-points of AB and CD respectively.
We need to prove that
Since E and F are the mid-points of AB and CD respectively.
Therefore,
,
And
,
Also, ABCD is a parallelogram. Therefore, the opposite sides should be equal.
Thus,
Also, (Because
)
Therefore, BEFC is a parallelogram
Then, and
…… (i)
Now,
Thus, (Because
as ABCD is a parallelogram)
We get,
AEFD is a parallelogram
Then, we get:
…… (ii)
But, E is the mid-point of AB.
Therefore,
Using (i) and (ii), we get:
Hence proved.
Page 14.57 Ex. 14.4
Q18.
Answer :
In BM and CN are perpendiculars on any line passing through A.
Also.
We need to prove that
From point L let us draw
It is given that ,
and
Therefore,
Since, L is the mid points of BC,
Therefore intercepts made by these parallel lines on MN will also be equal
Thus,
Now in ,
And . Thus, perpendicular bisects the opposite sides.
Therefore, is isosceles.
Hence
Hence proved.
Q19.
Answer :
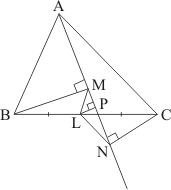
Figure can be drawn as:
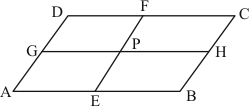
Let ABCD be a quadrilateral such that P,Q ,R and S are the mid-points of side AB,BC,CD and DA respectively.
In , P and Q are the mid-points of AB and BC respectively.
Therefore,
and
Similarly, we have
and
Thus,
and
Therefore, PQRS is a parallelogram.
Since, diagonals of a parallelogram bisect each other.
Therefore, PR and QS bisect each other.
Hence proved.
Q20.
Answer :
(i) The triangle formed by joining the mid-points of the sides of an isosceles triangle is isosceles.
Explanation:
Figure can be drawn as: A
, an isosceles triangle is given.
F and E are the mid-points of AB and AC respectively.
Therefore,
…… (I)
Similarly,
…… (II)
And
…… (III)
Now, is an isosceles triangle.
From equation (II) and (III), we get:
Therefore, in two sides are equal.
Therefore, it is an isosceles triangle.
(ii) The triangle formed by joining the mid-points of the sides of a right triangle is right triangle.
Explanation:
Figure can be drawn as: A
right angle at B is given.
F and E are the mid-points of AB and AC respectively.
Therefore,
…… (I)
Similarly,
…… (II)
And
…… (III)
Now, DE || AB and transversal CB and CA intersect them at D and E respectively.
Therefore,
and
Similarly,
Therefore,
and
Similarly,
Therefore,
Now AC is a straight line.
Now, by angle sum property of ,we get:
Therefore,
But,
Then we have:
(iii) The figure formed by joining the mid-points of the consecutive sides of a quadrilateral is parallelogram.
Explanation:
Figure can be drawn as:
Let ABCD be a quadrilateral such that P, Q, R and S are the mid-points of side AB, BC, CD and DA respectively.
In , P and Q are the mid-points of AB and BC respectively.
Therefore,
and
Similarly, we have
and
Thus,
and
Therefore, PQRS is a parallelogram.
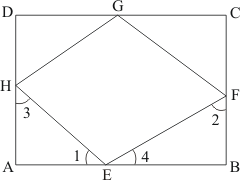
Page 14.62 Formative Assessment_VSA
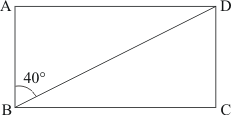
Q1.
In Parallelogram ABCD, and
are adjacent angles.
Thus, .
Then, we have and
as consecutive interior angles which must be supplementary.
Hence, the sum of and
is
.
Q2.
In Parallelogram ABCD , and
are Adjacent angles.
We know that in a parallelogram, adjacent angles are supplementary.
Now, ?A+?D=180°??A+115°=180°??A=180°-115°??A=65°So, measure of ?A is 65°.
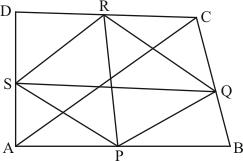
Q3.
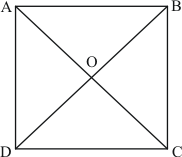
PQRS is a square given as:
Since the diagonals of a square intersect at right angle.
Therefore, the measure of is
.
Q4.
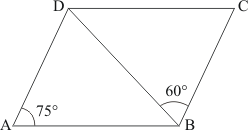
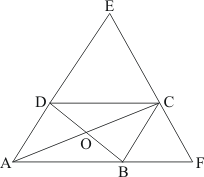
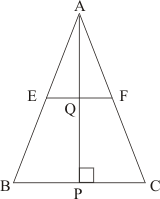
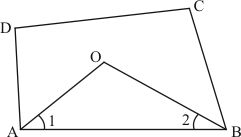
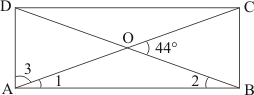
The quadrilateral can be drawn as follows:
We have AO and BO as the bisectors of angles and
respectively.
In ,We have,
…… (1)
By angle sum property of a quadrilateral, we have:
Putting in equation (1):
……(2)
It is given that in equation (2), we get:
Hence, the sum of and
is
.
Q5.
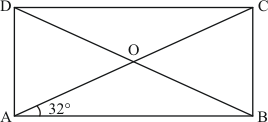
The rectangle ABCD is given as:
We have,
(Linear pair)
Since, diagonals of a rectangle are equal and they bisect each other. Therefore, in , we have
(Angles opposite to equal sides are equal.)
Therefore,
Now,in , we have
Since, each angle of a rectangle is a right angle.
Therefore,
Thus,
Hence, the measure of is.
Q6.
The square PQRS is given as:
Since PQRS is a square.
Therefore,
and
Now, in , we have
That is, (Angles opposite to equal sides are equal)
By angle sum property of a triangle.
(
)
Hence, the measure of is
.
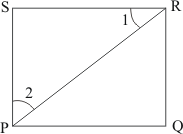
Q7.
Figure is given as :
Suppose the diagonals AC and BD intersect at O.
Since, diagonals of a rectangle are equal and they bisect each other.
Therefore, in , we have
Angles opposite to equal sides are equal.
Therefore,
But,
Now,
Hence, the measure of is
.
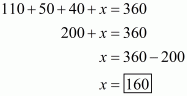
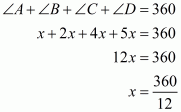
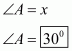
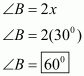
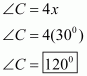
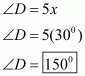
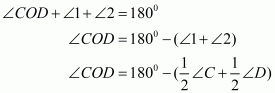
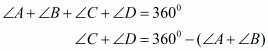
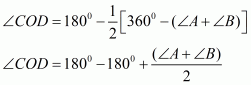
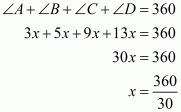
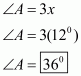
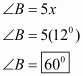
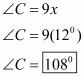
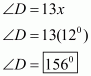
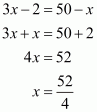
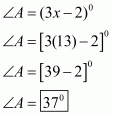
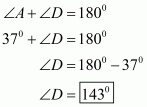
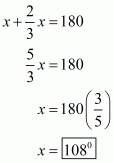
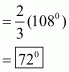
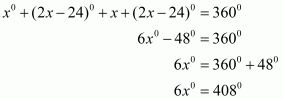
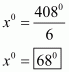
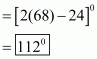
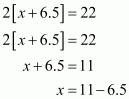
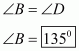
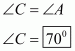
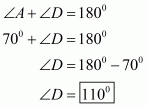
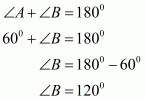
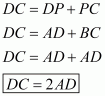
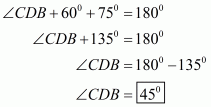
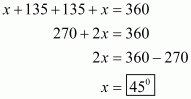
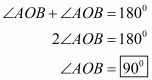
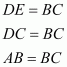
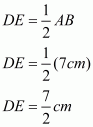
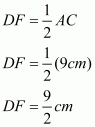
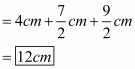
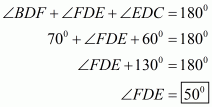
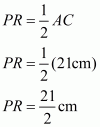
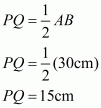
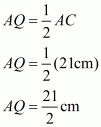
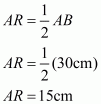
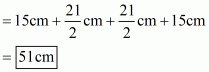
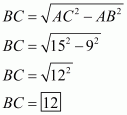
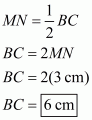
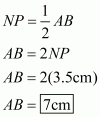
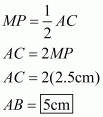
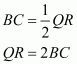
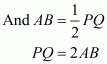
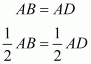
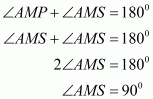
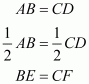
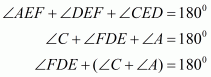
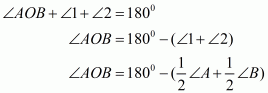
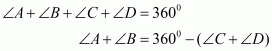
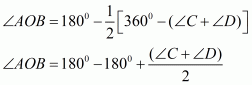
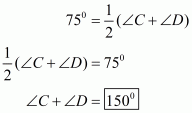
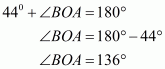
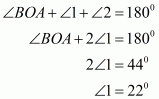
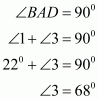
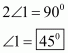
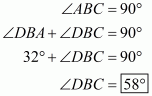

Leave a Reply