Notes For All Chapters Science Class 9
1. Introduction to Motion
1.1 What is Motion?
Motion means a change in the position of an object with time.
Everything around us moves in some way:
- Birds fly in the air.
- Fish swim in water.
- Cars move on roads.
- Blood flows through veins and arteries.
- Planets, stars, and galaxies are also in motion.
Motion can be of different types depending upon the type of path by which the object is going through.
(i) Circulatory motion/Circular motion – In a circular path.
(ii) Linear motion – In a straight line path.
1.2 Relative Nature of Motion
An object may appear moving for one observer but stationary for another.
Example:
For passengers in a moving bus, roadside trees appear to move backward.
For a person on the roadside, the bus appears to move forward.
But passengers inside the bus appear to be at rest relative to each other.
Conclusion:
Motion is relative — depends on the observer’s reference point.
2. Describing Motion
2.1 Reference Point (Origin)
To describe the location of an object, we specify a reference point or origin.
Example:
If a school is 2 km north of a railway station, the station is the reference point.
We can choose any convenient reference point.
3. Motion Along a Straight Line
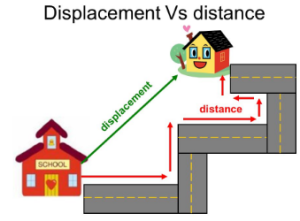
3.1 Distance and Displacement
| Concept | Definition | Type | Key Feature |
|---|---|---|---|
| Distance | Total path length covered by an object | Scalar | Depends only on path, not direction |
| Displacement | Shortest distance from the initial to the final position | Vector | Depends on direction |
Example
Object moves from O → A → B → C, then returns.
- Distance from O → A = 60 km
- Distance from A → C = 35 km
- Total Distance = 95 km
But displacement = Shortest distance from O to C = 35 km
Displacement ≠ Distance
Important Points
Distance ≥ Displacement
Displacement can be zero even when distance ≠ 0
Example: If object returns to starting point (O → A → O).
4. Uniform and Non-uniform Motion
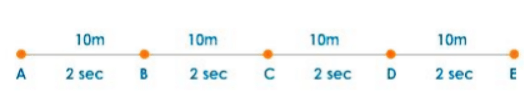
Uniform Motion: When a body travels equal distance in equal interval of time, then the motion is said to be uniform motion.
Non-uniform Motion: In this type of motion, the body will travel unequal distances in equal intervals of time.
Non-uniform motion is of two types :
(i) Accelerated Motion : When speed of a body increases with time.
(ii) De-accelerated Motion: When motion of a body decreases with time.
5. Measuring the Rate of Motion
5.1 Speed
The rate of motion of an object.
Speed (v)= \(\frac{Distance}{Time}\)
SI Unit → m/s (metre per second)
Other units → cm/s, km/h
Scalar quantity (no direction).
Average Speed
Example 7.1: An object travels 16 m in 4 s, then another 16 m in 2 s.
Average Speed = \(\frac{32}{6}\) = 5.33m/s
5.2 Velocity
Velocity = Speed in a given direction.
Vector quantity (has both magnitude and direction).
Changes if either speed or direction changes.
Average Velocity:
vav = \(\frac{u+v}{2}\)
where
u = initial velocity, v = final velocity.
Example 7.3:
Usha swims 180 m (back and forth in 90 m pool) in 1 min.
- Distance = 180 m → Average speed = 3 m/s
- Displacement = 0 → Average velocity = 0 m/s
6. Rate of Change of Velocity
6.1 Acceleration
The rate at which velocity changes with time.
a = \(\frac{v-u}{t}\)
where
v = final velocity, u = initial velocity, t = time taken.
- SI Unit: m/s²
- Positive acceleration → Speed increases.
- Negative acceleration (retardation/deceleration) → Speed decreases.
Example 7.4:
Rahul speeds up his bicycle from 0 to 6 m/s in 30 s.
a = \(\frac{6-0}{30}\) = 0.2m/s2
Then slows to 4 m/s in 5 s.
a = \(\frac{4-6}{5}\) = 0.4m/s2
7. Graphical Representation of Motion
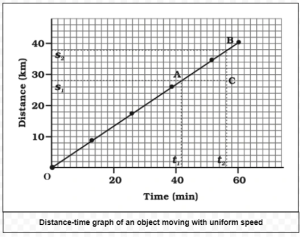
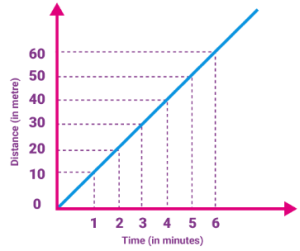
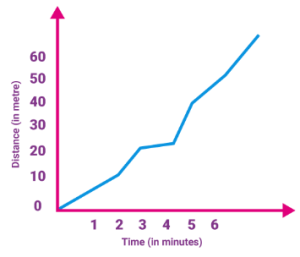
7.1 Distance–Time Graph
Time → X-axis, Distance → Y-axis
Shows how distance changes with time.
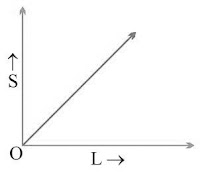
(a) Uniform Motion:
Straight line graph → Equal distances in equal times.
Speed = Slope of the graph
(b) Non-Uniform Motion:
Curved line graph → Unequal distances in equal times.
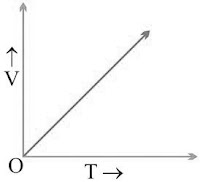
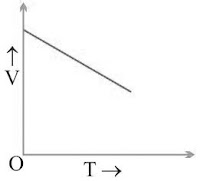
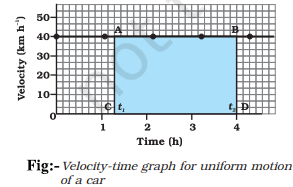
7.2 Velocity–Time Graph
- Time → X-axis, Velocity → Y-axis
- Uniform velocity: Straight line parallel to X-axis.
- Uniform acceleration: Straight line with slope.
- Non-uniform acceleration: Irregular curved line.
Finding Distance from Graph:
Distance = Area under the velocity–time graph
For uniform velocity:
Area = Rectangle under graph
For uniform acceleration:
Area = Rectangle + Triangle
s = AB×BC+\(\frac{1}{2}\)(AD×DE)
8. Equations of Motion (for Uniform Acceleration)
| Equation | Expression | Meaning |
|---|---|---|
| (i) | v = u + at | Final velocity after time t |
| (ii) | s = ut + ½ at² | Distance covered in time t |
| (iii) | v² – u² = 2as | Relation between velocity and distance |
where
u = initial velocity
v = final velocity
a = acceleration
s = distance
t = time
Example 7.6:
Car accelerates uniformly from 18 km/h to 36 km/h in 5 s.
u = 5m/s, v = 10m/s, t = 5s
(i) a = (v−u)/t = 1 m/s2
(ii) s = ut+\(\frac{1}{2}\)at2 = 37.5 m
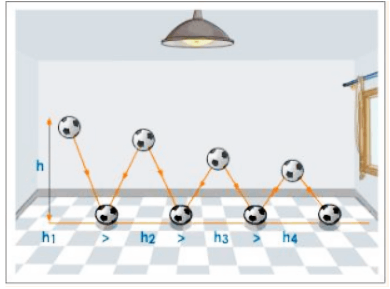
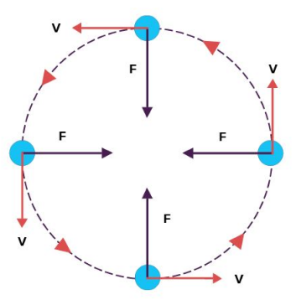
9. Uniform Circular Motion
Definition:
When an object moves in a circular path with constant speed, its motion is called Uniform Circular Motion.
Explanation:
- Speed remains constant, but direction changes continuously.
- Hence, velocity changes, and the object is accelerating.
Example:
- Moon revolving around Earth.
- Satellites around Earth.
- Cyclist moving on circular track.
Formula:
where
r = radius of the circle,
t = time to complete one revolution.
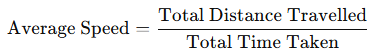
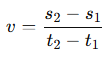
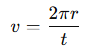


Please share me important notes fot 9th class
Thanks for free question Bank and notes
this was really helpful