Page 28.6 Ex 28.1
Q1.
Answer :
(i) The x-coordinate, the y-coordinate and the z-coordinate of the point (5, 2, 3) are all positive.
Therefore, this point lies in XOYZ octant.
(ii) The x-coordinate, the y-coordinate and the z-coordinate of the point (−5, 4, 3) are negative, positive and positive, respectively.
Therefore, this point lies in X’OYZ octant.
(iii) The x-coordinate, the y-coordinate and the z-coordinate of the point (4, −3, 5) are positive, negative and positive, respectively.
Therefore, this point lies in XOY’Z octant.
(iv) The x-coordinate, the y-coordinate and the z-coordinate of the point (7, 4, −3) are positive, positive and negative, respectively.
Therefore, this point lies in XOYZ’ octant.
(v) The x-coordinate, the y-coordinate and the z-coordinate of the point (−5, −4, 7) are negative, negative and positive, respectively.
Therefore, this point lies in X’OY’Z octant .
(vi) The x-coordinate, the y-coordinate and the z-coordinate of the point (−5, −3, −2) are all negative.
Therefore, this point lies in X’OY’Z’ octant
(vii) The x-coordinate, the y-coordinate and the z-coordinate of the point (2, −5, −7) are positive, negative and negative, respectively.
Therefore, this point lies in XOY’Z’ octant.
(viii) The x-coordinate, the y-coordinate and the z-coordinate of the point(−7, 2, −5) are negative, positive and negative, respectively.
Therefore, this point lies in X’OYZ’ octant.
Q2.
Answer :
(i) 2, 3, 4
(ii) -5,-4,-3
(iii) 5, 2, 7
(iv) -5, 0, 3
(v) -4, 0, 0
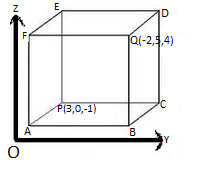
Q3.
Answer :
Let P≡(1, 0, −1)
The length of each side of the cube is 5.
The three edges from vertex of the cube are drawn from P towards the negative x and y axes and the positive z-axis.
Therefore, the coordinates of the vertex of the cube will be as follows:
x-coordinate = 1, 1-5 = -4, i.e. 1, -4
y-coordinate = 0, 0-5 = -5, i.e. 0, -5
z-coordinate = -1, -1 + 5 = 4, i.e. -1, 4
Hence, the remaining seven vertices of the cube are as follows:
1, 0, 41, -5, -11, -5, 4-4, 0, -1-4, 0, 4-4, -5, -1-4, -5, 4
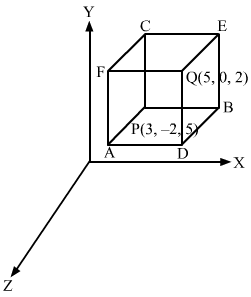
Q4.
Answer :
Let P≡(3, 0, −1), Q≡(−2, 5, 4)
PE = Distance between the parallel planes ABCP and FQDE
= 4+1=5
(These planes are perpendicular to the z-axis)
PA = Distance between the parallel planes ABQF and PCDE
= -2-3=5
(These planes are perpendicular to the x-axis)
Similarly, PC = 5-0=5
Thus, the length of the edges of the parallelepiped are 5, 5 and 5
Q5.
Answer :
Clearly, PBEC and QDAF are the planes parallel to the yz-plane such that their distances from the yz-plane are 5 and 3, respectively.
∴ PA = Distance between planes PBEC and QDAF
= 5 – 3
= 2
PB is the distance between planes PAFC and BDQE that are parallel to the zx-plane and are at distances 0 and -2, respectively, from the zx-plane.
∴PB = 0 – (-2)
= 2
PC is the distance between parallel planes PBDA and CEQF that are at distances 2 and 5, respectively, from the xy-plane.
∴ PC = 2 – 5
= -3
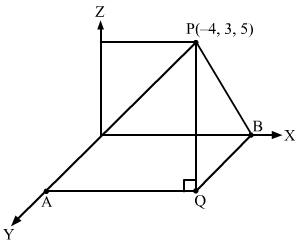
Q6.
Answer :
Let PQ be the perpendicular to the xy-plane and QA be perpendicular from Q to the y-axis.
PA will be perpendicular to the x-axis.
Also, QA = 3 and PQ = 5
Now, distance of P from the x-axis:
PB = BQ2+QP2
=32+52=9+25=34
Similarly,
From the right-angled ∆PAQ:
distance of P from the y-axis:
PA = AQ2+QP2
=-42+52=16+25=41
Similarly, the length of the perpendicular from P to the z-axis =-42+32
=16+9=25=5
Q7.
Answer :
The seven coordinates are as follows:
-3, 2, 53, 2, -5-3, -2, 53, -2, -5-3, 2, -5-3, -2, -53, 2, 5
Page 28.9 Ex 28.2
Q1.
Answer :
(i) PQ = x2-x12+y2-y12+z2-z12
= 2-12+1+12+2-02
= 12+22+22
= 1+4+4
= 9
= 3
(ii) AB = x2-x12+y2-y12+z2-z12
=-1-32+-1-22+-1+12=-42+-32+02=16+9+0=25=5
Q2.
Answer :
PQ = x2-x12+y2-y12+z2-z12
=2+22+1-32+2-12=42+-22+12=16+4+1=21 units
Q3.
Answer :
(i) AB = 5-42+-7+32+6+12
=12+-42+72=1+16+49=66
BC = 3-52+1+72+-8-62
= -22+82+-142
=4+64+196=264=266
AC = 3-42+1+32+-8+12
=-12+42+-72=1+16+49=66
Here , AB+AC=66+66 =266 =BC
Hence, the points are collinear.
(ii) PQ = 1-02+4-72+-5+72
=12+-32+22=1+9+4=14
QR = -1-12+10-42+-9+52
=-22+62+-42=4+36+16=56=214
PR=-1-02+10-72+-9+72
=-12+32+-22=1+9+4=14
Here, PQ+PR=14+14 =214 =QR
Hence, the points are collinear.
(iii) AB = -1-32+0+52+8-12
=-42+52+72=16+25+49=90=310
BC = 7+12+-10-02+-6-82
=82+-102+-142=64+100+196=360=610
AC = 7-32+-10+52+-6-12
=42+-52+-72=16+25+49=90=310
Here, AB+AC=310+310 =610 =BC
Hence, the points are collinear.
Q4.
Answer :
(i) We know that the z-coordinate of every point on the xy-plane is zero.
So, let P (x, y, 0) be a point on the xy-plane such that PA = PB = PC
Now, PA = PB
⇒PA2=PB2⇒x-12+y+12+0-02 =x-22+y-12+0-22⇒x2-2x+1+y2+2y+1=x2-4x+4+y2-2y+1+4⇒-2x+4x+2y+2y+2-9=0⇒2x+4y-7=0⇒2x+4y=7 …(1) PB=PC⇒ PB2=PC2⇒x-22+y-12+0-22=x-32+y-22+0+12⇒x2-4x+4+y2-2y+1+4=x2-6x+9+y2-4y+4+1⇒-4x+6x-2y+4y+9-14=0⇒2x+2y-5=0⇒x+y=52⇒x=52-y …2Putting the value of x in equation 1: 252-y+4y=7 ⇒5-2y+4y=7 ⇒5+2y=7 ⇒2y=2 ⇒ y=22∴y=1Putting the value of y in equation 2:x=52-1x=5-22x=32Hence, the required point is 32, 1, 0.
(ii) We know that the x-coordinate of every point on the yz-plane is zero.
So, let P (0, y, z) be a point on the yz-plane such that PA = PB = PC
Now, PA = PB
⇒0-12+y+12+z-02=0-22+y-12+z-22
⇒1+y2+2y+1+z2=4+y2-2y+1+z2-4z+4⇒2y+2=-2y-4z+9⇒2y+2y-4z=9-2⇒4y-4z=7⇒y-z=74 … 1PB=PC⇒PB2=PC2⇒0-22+y-12+z-22=0-32+y-22+z+12⇒4+y2-2y+1+z2-4z+4=9+y2-4y+4+z2+2z+1⇒-2y-4z+9=-4y+2z+14⇒-2y+4y-4z-2z=14-9⇒2y-6z=5⇒y-3z=52∴ y=52+3z 2Putting the value of y in equation 1: y-z=74⇒52+3z-z=74⇒2z=74-52⇒2z=7-104⇒2z=-34∴ z=-38Putting the value of z in equation 2: y=52+3z⇒y=52+3-38⇒y=52-98⇒y=20-98∴ y=118
Hence, the required point is 0,118,-38.
(iii) We know that the y-coordinate of every point on the zx-plane is zero.
So, let P (x, 0, z) be a point on the zx-plane such that PA = PB = PC
Now, PA = PB
⇒x-12+0+12+z-02=x-22+0-12+x-22
⇒x2+1-2x+1+z2=x2-4x+4+1+z2-4z+4⇒-2x+2=-4x-4z+9⇒-2x+4x-4z=7⇒2x-4z=7⇒x-2z=72 …1 PB=PC⇒PB2=PC2⇒x-22+0-12+z-22=x-32+0-22+z+12⇒x2-4x+4+1+z2-4z+4=x2-6x+9+4+z2+2z+1⇒-4x-4z+9=-6x+2z+14⇒-4x+6x-4z-2z=14-9⇒2x-6z=5⇒x-3z=52∴ x=52+3z …2Putting the value of x in equation 1: x-2z=72⇒52+3z-2z=72⇒52+z=72⇒z=72-52⇒z=7-52⇒z=22∴ z=1Putting the value of z in equation 2: x=52+3z⇒x=52+31⇒x=52+3⇒x=5+62∴ x=112
Hence, the required point is 112, 0, 1.
Q5.
Answer :
Let M be the point on the z-axis.
Then, the coordinates of M will be 0, 0, z.
Let M be equidistant from the points A 1, 5, 7 and B 5, 1, -4
AM = 0-12+0-52+z-72
=-12+-52+z-72=1+25+z2-14z+49=z2-14z+75
BM = 0-52+0-12+z+42
=-52+-12+z2+8z+16=25+1+z2+8z+16=z2+8z+42
Then, AM = BM
∴ z2-14z+75=z2+8z+42z2-14z+75=z2+8z+42-14z-8z=42-75-22z=-33z=3322z=32
Thus, the coordinates of M are 0, 0, 32.
Q6.
Answer :
Let the point on the y-axis be Y 0, y, 0 which is equidistant from the points P 3, 1, 2 and Q 5, 5, 2.
Then ,PY=QY
Now, 0-32+y-12+0-22=0-52+y-52+0-22
⇒-32+y2+2y+1+-22=-52+y-52+-22⇒9+y2+2y+1+4=25+y2+10y+25+4⇒y2+2y+14=y2+10y+54
⇒y2+2y+14=y2+10y+54
2y-10y=54-14-8y=40-y=408y=-5
Thus, the required point on the y-axis is (0, −5, 0).
Q7.
Answer :
Let the point be A (0, 0, z).Then,
AP = 21
⇒0-12+0-22+z-32=21⇒-12+-22+z-32=21⇒1+4+z-32=21⇒z-32=21-5⇒z-32=16⇒z-3=±4⇒z-3=4 or z-3=-4⇒z=7 or z=-1
Hence, the coordinates of the required point are (0, 0, 7) and (0, 0, −1).
Q8.
Answer :
Let A (1, 2, 3) , B (2, 3, 1) and C (3, 1, 2) are the coordinates of the triangle △ABC
AB = 2-12+3-22+1-32
=12+12+-22=1+1+4=6
BC = 3-22+1-32+2-12
=12+-22+12=1+4+1=6
AC = 3-12+1-22+2-32
=22+-12+-12=4+1+1=6
Now, AB = BC = AC
Therefore, it is an equilateral triangle.
Q9.
Answer :
Let A(0, 7, 10), B(-1, 6, 6), C(-4, 9, 6) be the coordinates of △ABC
Then, we have:
AB=0+12+7-62+10-62 =18 =32BC=-1+42+6-92+6-62 =18 =32AC=0+42+7-92+10-62 =36 =6Clearly, AB2+BC2=AC2 ⇒ ∠ABC=90°& AB=AC
Hence, △ABC is a right-angled isosceles triangle.
Q10.
Answer :
Let A(3,3,3) , B(0,6,3) , C( 1,7,7) and D (4,4,7) are the vertices of quadrilateral □ABCD
We have :
AB = 0-32+6-32+3-32
=-32+32+02=9+9+0=18=32
BC = 1-02+7-62+7-32
=12+12+42=1+1+16=18=32
CD = 4-12+4-72+7-72
=32+-32+02=9+9+0=18=32
DA = 4-32+4-32+7-32
=12+12+42=1+1+16=18=32
AB = BC = CD = DA
AC = 1-32+7-32+7-32
=-22+42+42=4+16+16=36=6
BD = 4-02+4-62+7-32
=42+-22+42=16+4+16=36=6
∴AC = BD
Since, all sides and diagonals of quadrilateral □ABCD are equal
Therefore, the points are the vertices of a square.
Q11.
Answer :
Let A(1,3,0),B(-5,5,2), C(-9,-1,2) and D(-3,-3,0) be the coordinates of quadrilateral□ABCD
AB=-5-12+5-32+2-02 =36+4+4 = 44BC=-9+52+-1-52+2-22 =16+36+0 =52 CD=-3+92+-3+12+0-22 =36+4+4 =44DA=1+32+3+32+0-02 =16+36+0 =52Here, we see that AB=CD& BC=DA
Since, opposite pair of sides are equal .
Therefore, □ABCD is a parallelogram .
AC=-9-12+-1-32+2-02 =-102+-42+22 =100+16+4 =120
BD=-3+52+-3-52+0-22 =22+-82+-22 =4+64+4 =72
∴AC≠ BD
∴ ABCD is not a rectangle.
Q12.
Answer :
Let A(1,3,4) , B(-1,6,10) , C(-7,4,7) and D (-5,1,1) be the vertices of quadrilateral □ ABCD
AB=-1-12+6-32+10-42 =4+9+36 =49 =7BC=-7+12+4-62+7-102 =36+4+9 =49 =7CD=-5+72+1-42+1-72 =4+9+36 =49 =7DA=1+52+3-12+4-12 =36+4+9 =49 =7∴ AB=BC=CD=DA
Hence, ABCD is a rhombus
Q13.
Answer :
The faces of a regular tetrahedron are equilateral triangles.
Let us consider △OAB
OA=0-02+0-12+0-12 =2
OB=1-02+0-02+1-02 =2
AB=1-02+0-12+1-12 =2
Hence, this face is an equilateral triangle.
Similarly, △OBC, △OAC, △ABC all are equilateral triangles.
Hence, the tetrahedron is a regular one.
Q14.
Answer :
Let the points be A (3, 2, 2), B (-1, 4, 2), C (0, 5, 6) and D (2, 1, 2) lie on the sphere
whose centre be P (1, 3, 4).
Since, AP, BP, CP and DP are radii.
Hence, AP = BP = CP = DP
AP=1-32+3-22+4-22 =-22+12+22 =4+1+4 =9 =3BP=1+12+3-42+4-22 =22+-12+22 =4+1+4 =9 =3CP=1-02+3-52+4-62 =12+-22+-22 =1+4+4 =9 =3DP=1-22+3-12+4-22 =-12+22+22 =1+4+4 =9 =3
Here, we see that AP = BP = CP = DP
Hence, A (3, 2, 2), B (-1, 4, 2), C (0, 5, 6) and D (2, 1, 2) lie on the sphere whose radius is 3 .
Q15.
Answer :
Let P (x, y, z) be the required point which is equidistant from the points O(0,0,0), A(2,0,0)
B(0,3,0) and C(0,0,8)
Then,
OP = AP
⇒OP2=AP2
∴ x2+y2+z2=x-22+y2+z2⇒x2=x-22⇒x2=x2-4x+4⇒4x=4⇒ x=44∴x=1
Similarly, we have:
OP = BP
⇒OP2=BP2
∴x2+y2+z2=x2+y-32+z2⇒y2=y2-6y+9⇒6y=9⇒ y=96∴ y=32
Similarly, we also have:
OP = CP
⇒OP2=CP2
⇒ x2+y2+z2=x2+y2+z-82⇒z2=z2-16z+64⇒16z=64⇒ z=6416∴ z=4
Thus, the required point is P 1, 32, 4.
Q16.
Answer :
Let coordinates of point P be (x, y, z).
Given:
3PA = 2PB
⇒3x+22+y-22+z-32=2x-132+y+32+z-132⇒3×2+4x+4+y2-4y+4+z2-6z+9=2×2-26x+169+y2+6y+9+z2-26z+169Squaring both sides,⇒9×2+y2+z2+4x-4y-6z+17=4×2+y2+z2-26x+6y-26z+347⇒9×2+9y2+9z2+36x-36y-54z+153=4×2+4y2+4z2-104x+24y-104z+1388⇒5×2+5y2+5z2+140x-60y+50z-1235=0⇒5×2+y2+z2+140x-60y+50z-1235=0∴5×2+y2+z2+140x-60y+50z-1235=0 is the locus of the point P.
Q17.
Answer :
Let P (x, y, z) be the point if PA2+PB2=2k2
⇒x-32+y-42+z-522+x+12+y-32+z+722=2k2⇒x2-6x+9+y2-8y+16+z2-10z+25+x2+2x+1+y2-6y+9+z2+14z+49=2k2⇒2×2+2y2+2z2-4x-14y+4z+109-2k2=0
Hence, 2×2+2y2+2z2-4x-14y+4z+109-2k2=0 is the locus of point P.
Page 28.10 Ex 28.2
Q18.
Answer :
Let A(a,b,c) , B(b,c,a) and C(c,a,b) be the vertices of △ABC. Then,
AB = b-a2+c-b2+a-c2
=b2-2ab+a2+c2-2bc+b2+a2-2ca+c2=2a2+2b2+2c2-2ab-2bc-2ca=2a2+b2+c2-ab-bc-ca
BC = c-b2+a-c2+b-a2
=c2-2bc+b2+a2-2ca+c2+b2-2ab+a2=2a2+2b2+2c2-2ab-2bc-2ca=2a2+b2+c2-ab-bc-ca
CA = a-c2+b-a2+c-b2
=a2-2ca+c2+b2-2ab+a2+c2-2bc+b2=2a2+2b2+2c2-2ab-2bc-2ca=2a2+b2+c2-ab-bc-ca
∴ AB = BC = CA
Therefore,△ABC is an equilateral triangle.
Q19.
Answer :
Let A(3,6,9), B(10,20,30) and C( 25,-41,5) are vertices of △ABC
AB = 10-32+20-62+30-92
=72+142+212=49+196+441=686=714
BC = 25-102+-41-202+5-302
=152+-612+-252=225+3721+625=4571
CA= 3-252+6+412+9-52
=-222+472+-42=484+2209+16=2709=3301
AB2+BC2=7142+45712 =686+4571 =5257CA2=2709∴ AB2+BC2≠CA2
A triangle △ABC is right-angled at B if CA2=AB2+BC2.
But, CA2 ≠ AB2+BC2
Hence, the points are not vertices of a right-angled triangle.
Q20.
Answer :
(i) Let A(0, 7, -10) , B(1, 6, -6) , C(4, 9, -6) be the vertices of △ABC.Then,
AB = 1-02+6-72+-6+102
=12+-12+42=1+1+16=18=32
BC = 4-12+9-62+-6+62
=32+32+0=9+9=18=32
CA= 0-42+7-92+-10+62
=16+4+16=36=6
Clearly, AB = BC
Thus, the given points are the vertices of an isosceles triangle.
(ii) Let A(0,7,10) , B( -1,6,6) and C( -4,9,6) be the vertices of △ABC. Then ,
AB = -1-02+6-72+6-102
=-12+-12+-42=1+1+16=18=32
BC = -4+12+9-62+6-62
=-32+32+0=9+9=18=32
AC = -4-02+9-72+6-102
=-42+22+-42=16+4+16=36=6
AC2=AB2+BC2
Thus, the given points are the vertices of a right-angled triangle.
(iii) Let A(-1, 2, 1) , B(1, -2, 5) , C(4, -7, 8), D(2, -3, 4) be the vertices of quadrilateral □ABCD
AB=1+12+-2-22+5-12 =4+16+16 =36 =6BC=4-12+-7+22+8-52 =9+25+9 =43CD=2-42+-3+72+4-82 =4+16+16 =36 =6DA=-1-22+2+32+1-42 =9+25+9 =43∴ AB=CD and BC=DA
Since, each pair of opposite sides are equal.
Thus, quadrilateral □ABCD is a parallelogram.
Q21.
Answer :
Let P (x, y, z) be any point that is equidistant from the points A (1, 2, 3) and B (3, 2, −1).
Then, we have:
PA = PB
⇒ x-12+y-22+z-32=x-32+y-22+z+12⇒ x2-2x-1+y2-4y+4+z2-6z+9=x2-6x+9+y2-4y+4+z2+2z+1⇒-2x-4y-6z+14=-6x-4y+2z+14⇒-2x+6x-4y+4y-6z-2z=14-14⇒4x-8z=0⇒x-2z=0
Hence, the locus is x – 2z = 0
Q22.
Answer :
Let P (x, y, z) be any point , the sum of whose distance from the points A(4,0,0) and B(-4,0,0)
is equal to 10. Then,
PA + PB = 10
⇒x-42+y-02+z-02+x+42+y-02+z-02=10⇒x+42+y-02+z-02=10-x-42+y-02+z-02⇒x2+8x+16+y2+z2=10-x2-8x+16+y2+z2
⇒x2+8x+16+y2+z2=100+x2-8x+16+y2+z2-20×2-8x+16+y2+z2⇒16x-100=-20×2-8x+16+y2+z2⇒4x-25=-5×2-8x+16+y2+z2⇒16×2-200x+625=25×2-8x+16+y2+z2⇒16×2-200x+625=25×2-200x+400+25y2+25z2⇒9×2+25y2+25z2-225=0
∴ 9×2+25y2+25z2-225=0 is the required locus .
Q23.
Answer :
To show that ABCD is a parallelogram, we need to show that its two opposite sides are equal.
AB=-1-12+-2-22+-1-32 =4+16+16 =36 =6BC=2+12+3+22+2+12 =9+25+9 =43CD=4-22+7-32+6-22 =4+16+16 =36 =6DA=1-42+2-72+3-62 =9+25+9 =43AB=CD and BC=DASince, opposite pairs of sides are equal .∴ABCD is a parallelogramAC=2-12+3-22+2-32 =1+1+1 =3BD=4+12+7+22+6+12 =25+81+49 =155Since, AC≠BD
Thus, ABCD is not a rectangle.
Q24.
Answer :
Let P (x, y, z) be any point which is equidistant from A (3,4,5) and B (-2,1,4) .Then,
PA = PB
⇒x-32+y-42+z+52=x+22+y-12+z-42⇒x2-6x+9+y2-8y+16+z2+10z+25=x2+4x+4+y2-2y+1+z2-8z+16⇒x2-6x+9+y2-8y+16+z2+10z+25=x2+4x+4+y2-2y+1+z2-8z+16⇒-10x-6y+18z+29=0∴10x+6y-18z-29=0
Hence, 10x + 6y -18z -29 = 0 is the required equation.
Page 28.17 Ex 28.3
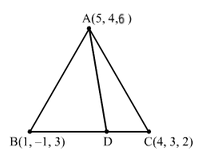
Q1.
Answer :
AB = 42+52+32=16+25+9=50=52
AC = 12+12+42=18=32
AD is the internal bisector of ∠BAC.
∴BDDC=ABAC=53
Thus, D divides BC internally in the ratio 5:3.
∴ D≡5×4+3×15+3, 5×3+3-15+3, 5×2+3×35+3⇒ D≡238, 128, 198⇒ D≡238, 32, 198 ∴ AD=5-2382+4-1282+6-1982 =172+202+29282 =289+400+84182 =15308
Q2.
Answer :
Suppose C divides AB in the ratio λ:1.
Then, the coordinates of C are 8λ+2λ+1, -3λ+1, 10λ+4λ+1.
The z-coordinate of C is 8.
∴ 10λ+4λ+1=8⇒10λ+4=8λ+8⇒2λ=4∴ λ=2
Hence, the coordinates of C are as follows:
8λ+2λ+1, -3λ+1, 10λ+4λ+1⇒8×2+22+1, -32+1, 10×2+42+1⇒183, -33, 243∴ 6, -1, 8
Hence, the coordinates of C are (6, −1, 8).
Q3.
Answer :
Suppose C divides AB in the ratio λ:1.
Then, the coordinates of C are -λ+2λ+1, 2λ+3λ+1, -3λ+4λ+1.
But, the coordinates of C are (-4, 1, -10).
∴ -λ+2λ+1=-4, 2λ+3λ+1=1, -3λ+4λ+1=-10⇒-λ+2=-4λ-4, 2λ+3=λ+1, -3λ+4=-10λ-10⇒3λ=-6, λ=-2, 7λ=-14∴ λ=-2, λ=-2, λ=-2
From these three equations, we have:
λ=-2
So, C divides AB in the ratio 2:1 (externally).
Q4.
Answer :
Let A≡(2, 4, 5) and B≡(3, 5, 4)
Let the line joining A and B be divided by the yz-plane at point P in the ratio λ:1.
Then, we have:
P≡3λ+2λ+1, 5λ+4λ+1, 4λ+5λ+1
Since P lies on the yz-plane, the x-coordinate of P will be zero.
∴3λ+2λ+1=0 ⇒3λ+2=0∴λ=-23
Hence, the yz-plane divides AB in the ratio 2:3 (externally).
Q5.
Answer :
Suppose the plane x + y + z = 5 divides the line joining the points A (2, −1, 3) and B (-1, 2, 1) at a point C in the ratio λ:1.
Then, coordinates of C are as follows:
-λ+2λ+1, 2λ-1λ+1, λ+3λ+1
Now, the point C lies on the plane x + y + z = 5.
Therefore, the coordinates of C must satisfy the equation of the plane.
-λ+2λ+1+2λ-1λ+1+λ+3λ+1=5⇒-λ+2+2λ-1+λ+3=5λ+5⇒2λ+4=5λ+5⇒-3λ=1∴λ=-13
So, the required ratio is 1:3 (externally).
Q6.
Answer :
Suppose C divides AB in the ratio λ:1.
Then, coordinates of C are as follows:
9λ+3λ+1, 8λ+2λ+1, -10λ-4λ+1
But, the coordinates of C are (5, 4, -6).
∴ 9λ+3λ+1=5, 8λ+2λ+1=4, -10λ-4λ+1=-6
These three equations give λ=12.
So, C divides AB in the ratio 1:2.
Q7.
Answer :
Let D x1, y1, z1, E x2 ,y2, z2 and F x3, y3, z3 be the vertices of the given triangle.
And, let A -2, 3, 5, B 4, -1, 7 and C 6, 5, 3 be the mid-points of the sides EF, FA and DE, respectively.
Now, A is the mid-point of EF.
∴x2+x32=-2, y2+y32=3, z2+z32=5⇒x2+x3=-4, y2+y3=6, z2+z3=10………………. i
B is the mid-point of FD.
∴x1+x32=4, y1+y32=-1, z1+z32=7⇒x1+x3=8, y1+y3=-2, z1+z3=14 …………………ii
C is the mid-point of DE.
∴x1+x22=6, y1+y22=5, z1+z22=3⇒x1+x2=12, y1+y2=10, z1+z2=6…………………… iii
Adding the first three equations in (i), (ii) and (iii):
2×1+x2+x3=-4+8+12⇒x1+x2+x3=8
Solving the first three equations in (i), (ii) and (iii) with x1+x2+x3=8:
x1=12, x2=0, x3=-4
Adding the next three equations in (i), (ii) and (iii):
2y1+y2+y3=6-2+10⇒y1+y2+y3=7
Solving the next three equations in (i), (ii) and (iii) with y1+y2+y3=7:
y1=1, y2=9, y3=-3
Adding the last three equations in (i), (ii) and (iii):
2z1+z2+z3=10+14+6⇒z1+z2+z3=15
Solving the last three equations in (i), (ii) and (iii) with z1+z2+z3=15:
z1=5, z2=1, z3=9
Thus, the vertices of the triangle are (12, 1, 5), (0, 9, 1), (−4, −3, 9).
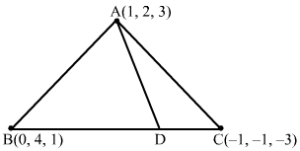
Q8.
Answer :
AB = -12+22+-22=1+4+4=9=3
AC = -22+-32+-62=4+9+36=49=7
AD is the internal bisector of ∠BAC.
∴BDDC=ABAC=37
Thus, D divides BC internally in the ratio 3:7.
∴D≡3-1+3×03+7, 3-1+743+7, 3-3+7×13+7⇒ D≡-310, 2510, -210⇒ D≡-310, 52, -15
Q9.
Answer :
Let the sphere meet the line joining the given points at the point (x1, y1, z1).
Then, we have:
Suppose the point (x1, y1, z1) divides the line joining the points (12, – 4, 8) and (27, – 9, 18) in the ratio λ:1.
∴
Substitute these values in equation (1):
Thus, the sphere divides the line joining the given points in the ratio 2:3 and 2:– 3.
Hence, the given sphere divides the line joining the points (12, – 4, 8) and (27, – 9, 18) internally in the ratio 2:3 and externally in the ratio −2:3.
Q10.
Answer :
Let:
A = (x1, y1, z1)
B = (x2, y2, z2)
Now, let the line joining A and B be divided by the plane ax + by + cz + d = 0 at point P in the ratio λ:1.
∴ P = λx2+x1λ+1, λy2+y1λ+1, λz2+z1λ+1
Since P lies on the given plane,
ax + by + cz + d = 0
Thus,
aλx2+x1λ+1+bλy2+y1λ+1+cλz2+z1λ+1+d=0⇒aλx2+x1+bλy2+y1+cλz2+z1+dλ+1=0⇒λax2+by2+cz2+d+ax1+by1+cz1+d=0⇒λax2+by2+cz2+d=-ax1+by1+cz1+d⇒λ=-ax1+by1+cz1+dax2+by2+cz2+d⇒λ=-ax1+by1+cz1+dax2+by2+cz2+dThus, the given plane divides the line joining x1, y1, z1 and x2, y2, z2 in the ratio -ax1+by1+cz1+dax2+by2+cz2+d.
Q11.
Answer :
Let Ax1, y1, z1, Bx2, y2, z2 and Cx3, y3, z3 be the vertices of the given triangle,and let D1, 2,-3 , E3, 0, 1 and F-1, 1,-4 be the mid points of the sides BC, CA and AB respectively.D is the mid point of BC∴ x2+x32=1, y2+y32=2 and z2+z32=-3⇒x2+x3=2, y2+y3=4 and z2+z3=-6 …1E is the mid point of CA∴ x1+x32=3, y1+y32=0 and z1+z32=1⇒x1+x3=6, y1+y3=0 and z1+z3=2 …2F is the mid point of AB∴ x1+x22=-1, y1+y22=1 and z1+z22=-4⇒x1+x2=-2, y1+y2=2 and z1+z2=-8 …2Adding first three equations we get,2×1+x2+x3=6, 2y1+y2+y3=6 and 2z1+z2+z3=-12⇒x1+x2+x3=3, y1+y2+y3=3 and z1+z2+z3=-6.
The coordinate of the centroid is given by x1+x2+x33, y1+y2+y33,z1+z2+z33⇒1, 1, -2
Q12.
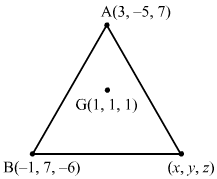
Answer :
Let G be the centroid of ∆ABC.
Given: G≡1, 1, 1
Let C≡x, y, z
Then, 1=3-1+x3 ⇒ 3=3-1+x ⇒3=2+x⇒ x=1and 1=-5+7+y3 ⇒ 3=2+y ⇒y=1and 1=7-6+z3 ⇒ 3=1+z ⇒z=2
∴C≡1, 1, 2
Q13.
Answer :
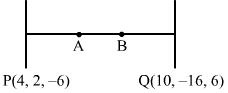
Let P≡(4, 2, -6) and Q≡(10, -16, 6)
Let A and B be the point of trisection.
Then, we have:
PA = AB = BQ
∴ PA:AQ = 1:2
Thus, A divides PQ internally in the ratio 1:2.
∴ A≡1×10+2×41+2, 1×-16+2×21+2, 1×6+2×-61+2
≡10+83, -16+43, 6-123≡183, -123, -63≡6, -4, -2
⇒ A≡(6, -4, -2)
AB = BQ
Therefore, B is the mid-point of AQ.
∴ B≡6+102, -4-162, -2+62
≡162, -202, 42≡8, -10, 2
⇒ B≡(8, -10, 2)
Q14.
Answer :
Let, C divides AB in the ratio λ:1.
Then, coordinates of C are -λ+2λ+1,2λ-3λ+1,λ+4λ+1.
But, the coordinates of C are 0, 13, 2.
∴ -λ+2λ+1=0 , 2λ-3λ+1=13, λ+4λ+1 = 2
From each of these equations, we get λ=2.
Since each of these equations give the same value of λ.
Therefore, the given points are collinear.
Q15.
Answer :
Let Q divide PR in the ratio λ:1
Thus, the coordinates of Q are as follows:
9λ+3λ+1, 8λ+2λ+1, -10λ-4λ+1
But, the coordinates of Q are (5, 4, −6) .
∴ 9λ+3λ+1=5 , 8λ+2λ+1=4 , -10λ-4λ+1=-6
These three equation gives λ=12.
So, Q divides PR in the ratio 12:1 or 1:2
Q16.
Answer :
Let A = (4, 8, 10) , B = (6, 10, -8)
Let the line joining A and B be divided by the YZ-plane at point P in the ratio λ:1.
∴ P=6λ+4λ+1, 10λ+8λ+1, -8λ+10λ+1
Since P lies on the YZ-plane, the x-coordinate of P will be zero.
∴6λ+4λ+1=0⇒6λ+4=0⇒6λ=-4∴ λ=-23
Hence, the YZ-plane divides AB in the ratio 2:3 (externally)
Page 28.18 (Multiple Choice Questions)
Q1.
Answer :
(c) -2 : 3
Let A≡(2, 4, 5) and B≡(3, 5, -9)
Let the line joining A and B be divided by the yz-plane at point P in the ratio λ:1.
Then, we have,
P≡3λ+2λ+1, 5λ+4λ+1, -9λ+5λ+1
Since P lies on the yz-plane, the x-coordinate of P will be zero.
∴3λ+2λ+1=0⇒3λ+2=0⇒λ=-23
Hence, the yz-plane divides AB in the ratio -2 : 3
Q2.
Answer :
(d) c : b
Let A≡(a, b, c) and B≡(-a, -c, -b)
Let the line joining A and B be divided by the xy-plane at point P in the ratio λ:1.
Then, we have,
P≡-aλ+aλ+1, -cλ+bλ+1, -bλ+cλ+1
Since P lies on the xy-plane, the z-coordinate of P will be zero.
∴-bλ+cλ+1=0⇒-bλ+c=0⇒λ=cb
Hence, the xz-plane divides AB in the ratio c : b
Q3.
Answer :
(d) π2
PQ2=4-02+-2-12+1-22=16+9+1=26OP2=0-02+1-02+2-02=0+1+4=5QO2=0-42+0+22+0-12=16+1+4=21Since, PQ2=OP2+QO2Hence, ∠POQ=π2
Q4.
Answer :
(b) 3
Length of the diagonal = 2-12+-3+22+5-32=1+1+4=6
∴ Length of the side = Length of diagonal2=62=3
Q5.
Answer :
(d) None of these
Suppose:
A(5, –4, 2)
B(4, –3, 1)
C(7, 6, 4)
D(8, –7, 5)
AB=4-52+-3+42+1-22 =-12+12+-12 =1+1+1=3BC=7-42+6+32+4-12 =32+92+32 =9+81+9=99=311CD=8-72+-7-62+5-42 =12+-132+12 =1+169+1=171DA=8-52+-7+42+5-22 =32+-32+32 =9+9+9=27=33
We see that none of the sides are equal.
Q6.
Answer :
(c) curves
Since, there is only one variable in the given equation. Also, it is quadratic equation.
Hence, It represents curves in yz plane.
Q7.
Answer :
(b) 3
Suppose d is the diameter of the sphere. Then
d2=-1-32+2-42+3+12⇒d2=-42+-22+42⇒d2=16+4+16⇒d2=36⇒ d=6
Hence, radius of the sphere is 3 units.
Q8.
Answer :
(c) −3:7
Let A≡(2, 3, 1) and B≡(6, 7, 1)
Let the line joining A and B be divided by the xz-plane at point P in the ratio λ:1.
Then, we have,
P≡6λ+2λ+1, 7λ+3λ+1, λ+1λ+1
Since P lies on the xz-plane, the y-coordinate of P will be zero.
∴7λ+3λ+1=0⇒7λ+3=0⇒λ=-37
Hence, the xz-plane divides AB in the ratio -3 : 7
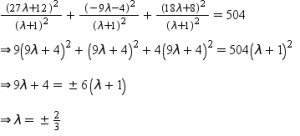

Leave a Reply