Page No.33.6 Ex.33.1
Q1.
Answer :
If a coin is tossed once, the possible outcomes are a head (H) and tail (T).
Therefore, the sample space of this experiment is S = { H, T}.
Q2.
Answer :
If a coin is tossed twice, the possible outcomes are HH, HT, TH, TT.
Therefore, the sample space of this experiment is S = {HH, HT, TH, TT}.
Q3.
Answer :
A coin has two faces: a head (H) and a tail (T).
When a coin is tossed three times, the total number of possible outcomes is 23 = 8.
Thus, when a coin is tossed three times, the sample space is given by S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}.
Q4.
Answer :
When a coin is tossed once, there are two possible outcomes: a head (H) and a tail (T).
When a coin is tossed four times, the total number of possible outcomes is 24 = 16.
Thus, when a coin is tossed four times, the sample space is given by
S = {HHHH, HHHT, HHTH, HHTT, HTHH, HTHT, HTTH, HTTT, THHH, THHT, THTH, THTT, TTHH, TTHT, TTTH, TTTT}
Q5.
Answer :
When two dices are thrown, there are (6 × 6) = 36 outcomes.
The set of these outcomes is the sample space, which is given by
S = (1, 1) , (1, 2), (1, 3), (1, 4), (1, 5), (1, 6)
(2, 1) , (2, 2), (2, 3), (2, 4), (2, 5), (2, 6)
(3, 1) , (3, 2), (3, 3), (3, 4), (3, 5), (3, 6)
(4, 1) , (4, 2), (4, 3), (4, 4), (4, 5), (4, 6)
(5, 1) , (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)
(6, 1) , (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)
Q6.
Answer :
When we throw a dice, it can result in any of the six numbers, namely 1, 2, 3, 4, 5 and 6.
When three dices are thrown together, the total number of elementary events associated is 63 = ( 6 × 6 × 6) = 216.
Q7.
Answer :
When a coin is tossed, the outcomes are H, T. When a dice is thrown, the outcomes can be 1, 2, 3, 4, 5, 6.
Thus, we can write the two parts of this experiment as follows:
Hence, the sample space is given by
S = {(H, 1), (H, 2), (H, 3), (H, 4), (H, 5), (H, 6),
(T, 1), (T, 2), (T, 3), (T, 4), (T, 5), (T, 6)}
Q8.
Answer :
A coin has two faces: a head (H) and a tail (T).
A dice has six faces that are numbered from 1, 2, 3, 4, 5, 6 with one number on each face.
When a head is shown on a coin toss, a dice is rolled.
Thus, the sample space is given by
S = {(H, 1),(H, 2), (H, 3), (H, 4), (H, 5), (H, 6), T}
Q9.
Answer :
When a coin is tossed twice, the possible outcomes are HH, HT, TH, TT.
The second throw results in a head in HH, TH.
The second throw results in a tail in HT, TT.
Now, a dice is thrown.
The possible outcomes on a dice are 1, 2, 3, 4, 5 and 6.
The sample space is given by
S = { HH, TH, (HT, 1), (HT, 2), (HT, 3), (HT, 4), (HT, 5), (HT, 6), (TT, 1), (TT, 2), (TT, 3) (TT, 4), (TT, 5), (TT 6)}.
∴ The total number of elements of the sample space is 14.
Q10.
Answer :
A coin has two faces: a head (H) and a tail (T).
A dice has six faces that are numbered from 1 to 6, with one number on each face.
Thus, the sample space of the given experiment is given by
S = {(H, H), (H, T), (T, 1), (T, 2), (T, 3), (T, 4), (T, 5), (T, 6)}
Q11.
Answer :
The box contains two red balls and three black balls.
Let us denote the red balls as R1 and R2 and the three black balls as B1, B2 and B3.
The sample space of this experiment is given by
S = {(T, R1), (T, R2), (T, B1), (T, B2), (T, B3), (H, 1), (H, 2), (H, 3), (H, 4), (H, 5), (H, 6)}.
Page No.33.7 Ex.33.1
Q12.
Answer :
In this experiment, a tail (T) may come up on the first throw, the second throw, the third throw and so on, until T is obtained.
This process continues indefinitely.
Hence, the sample space of this experiment is given by
S = {T, HT, HHT, HHHT, HHHHT, HHHHHT, …}
Q13.
Answer :
The box contains one red ball and three black balls.
Let us denote the red ball as R and the three black balls as B1, B2 and B3.
The sample space of this experiment is given by
S = {(R, B1), (R, B2), (R, B3), (B1, R), (B1, B2), (B1, B3), (B2, B1), (B2, B3), (B2, R), (B3, R), (B3, B1), (B3, B2)}
Q14.
Answer :
If a pair of dices is thrown simultaneously, then all possible outcomes = 6 × 6 = 36
The set of these outcomes is the sample space, which is given by
S = { (1, 1) , (1, 2), (1, 3), (1, 4), (1, 5), (1, 6)
(2, 1) , (2, 2), (2, 3), (2, 4), (2, 5), (2, 6)
(3, 1) , (3, 2), (3, 3), (3, 4), (3, 5), (3, 6)
(4, 1) , (4, 2), (4, 3), (4, 4), (4, 5), (4, 6)
(5, 1) , (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)
(6, 1) , (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
Again, if the outcome is a doublet, then a coin is tossed.
Now, we have the following events:
{(1, 1, H), (2, 2, H), (3, 3, H), (4, 4, H), (5, 5, H), (6, 6, H),
(1, 1, T), (2, 2, T), (3, 3, T), (4, 4, T), (5, 5, T), (6, 6, T)}
Total number of events when the outcome is a doublet = 6 x 2 = 12
Hence, the total number of elementary events associated with this experiment = (36 − 6) + 12 = 42
Q15.
Answer :
When a coin is tossed, the possible outcomes are head (H) and tail (T).
If a coin is tossed twice, the possible outcomes are given by
S = {HH, HT, TH, TT}
Again, if the second draw results in a head, then a dice is rolled. The events associated with this experiment is given by
A = {(HH, 1), (HH, 2), (HH, 3), (HH, 4), (HH, 5), (HH, 6), (TH, 1), (TH, 2), (TH, 3), (TH, 4), (TH, 5), (TH, 6)}
Hence, the sample space for this experiment is given by
(S ∪ A) = {(HH, 1), (HH, 2), (HH, 3), (HH, 4), (HH, 5), (HH, 6), (TH, 1),
(TH, 2), (TH, 3), (TH, 4), (TH, 5), (TH, 6), (HT), (TT)}
Q16.
Answer :
A bag contains four identical red balls (R) and three identical black balls (B).
The sample space S of drawing one ball with replacement and then again drawing a ball is given by
S = {RR, RB, BR, BB}
Q17.
Answer :
Three items are to be selected at random from a lot.
Each item in the lot is tested and classified as defective (D) or non-defective (N).
The sample space of this experiment is given by
S = {DDD, DDN, DND, DNN, NDD, NDN, NND, NNN}
Q18.
Answer :
(i) When the order of the birth of a girl or a boy is considered, the sample space is given by
S = {(G1, G2), (G1, B2), (B1 ,G2), (B1, B2)}
(ii) Since the maximum number of children in each family is two, a family can either have two boys or one boy or no boy.
Hence, the required sample space is given by
S = {0, 1, 2}
Q19.
Answer :
A dice has six faces that are numbered from 1 to 6, with one number on each face.
Let us denote the red, white and black dices as R, W, and B, respectively.
Accordingly, when a dice is selected and then rolled, the sample space is given by
S = {(R, 1), (R, 2), (R, 3), (R, 4), (R, 5), (R, 6),
(B, 1), (B, 2), (B, 3), (B, 4), (B, 5), (B, 6),
(W, 1), (W, 2), (W, 3), (W, 4), (W, 5), (W, 6)}
Q20.
Answer :
Let us denote two boys and two girls in room P as B1, B2 and G1, G2, respectively.
Let us denote one boy and three girls in room Q as B3 and G3, G4, G5, respectively.
Accordingly, the required sample space is given by S = {(P, B1), (P, B2), (P, G1), (P, G2) (Q, B3), (Q, G3), (Q, G4),
(Q, G5)}.
Q21.
Answer :
A bag contains one white ball (W) and one red ball (R).
When one ball is drawn, it will be either W or R.
The sample space of drawing one white ball with replacement and then again drawing a ball is {(W, W), (W, R)}.
Again, if red ball is drawn, a dice is rolled.
The sample space associated with this experiment is given by {(R, 1), (R, 2), (R, 3), (R, 4), (R, 5), (R, 6)}.
Hence, the sample space S for this experiment is S = {(W, W), (W, R), (R, 1), (R, 2), (R, 3), (R, 4), (R, 5), (R, 6)}.
Q22.
Answer :
It is given that the box contains one white ball and three identical black balls.
Let us denote the white ball with W and a black ball with B.
When two balls are drawn at random in succession without replacement, the sample space for this experiment will be given by
S = {WB, BW, BB}
Q23.
Answer :
A dice has six faces that are numbered from 1 to 6, with one number on each face.
Here, 2, 4 and 6 are even numbers, while 1, 3 and 5 are odd numbers.
A coin has two faces: a head (H) and a tail (T).
Hence, the sample space of this experiment is given by
S = { (2, H), (2, T), (4, H), (4, T), (6, H), (6, T), (1, HH), (1, HT), (1,TH), (1, TT), (3, HH), (3, HT), (3, TH), (3, TT),
(5, HH), (5, HT), (5, TH), (5, TT) }
Q24.
Answer :
In this experiment, 6 may come up on the first throw, the second throw, the third throw and so on, until it is obtained.
Hence, the sample space of this experiment is given by
S = {6, (1, 6), (2, 6), (3, 6), (4, 6), (5, 6), (1, 1, 6), (1, 2, 6), (1, 3, 6), (1, 4, 6), (1, 5, 6), (2, 1, 6), (2, 2, 6), (2, 3, 6) …}
Page No.33.17 Ex.33.2
Q1.
Answer :
In tossing a fair coin, there are two possible outcomes, namely Head (H) and Tail (T).
Hence, the sample space in this experiment is given by S = {H, T}.
Thus, total number of elementary events = 2
In all, there are four subsets of S: {H}, {T}, {H, T} and Φ.
Each of the subsets of the sample space is an event.
∴ There are 4 total events associated with the random experiment.
Note: If there are n elements in a set, then the number of its subset is 2n.
Q2.
Answer :
The events associated with the random experiment of tossing of two coins are HH, HT, TH and TT. These 4 events are also the elementary events when two unbiased coins are tossed simultaneously.
Q3.
Answer :
When three coins are tossed, the sample space is given by
S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
Accordingly, we have:
A = {HHH}
B = {HHT, HTH, THH}
C = {TTT}
D = {HHH, HHT, HTH, HTT}
Now, we observe that
A ∩ B = Φ; A ∩ C = Φ; A ∩ D = {HHH} ≠ Φ; B ∩ C = Φ; B ∩ D = {HHT, {HTH} ≠ Φ and C ∩ D = Φ
(i) Events A and B; events A and C; events B and C and events C and D are all mutually exclusive.
(ii) If an event has only one sample point of a sample space, it is called an elementary event.
Thus, A and C are elementary events.
(iii) If an event has more than one sample point of a sample space, it is called a compound event.
Thus, B and D are compound events.
Q4.
Answer :
When a dice is thrown, the sample space is given by S = {1, 2, 3, 4, 5, 6}.
Accordingly, we have:
(i) A = {1, 2, 3, 4, 5, 6}
(ii) B = Φ
(iii) C = {3, 6}
(iv) D = {1, 2, 3}
(v) E = {6}
(vi) F = {3, 4, 5, 6}
Here, A = {1, 2, 3, 4, 5, 6} and B = Φ
∴ A ∪ B = {1, 2, 3, 4, 5, 6}
Here, A = {1, 2, 3, 4, 5, 6} and B = Φ
∴ A ∩ B = Φ
Here, B = Φ and C = {3, 6}
∴ B ∩ C = Φ
Here, E = {6} and F = {3, 4, 5, 6}
∴ E ∩ F = {6}
Here, D = {1, 2, 3} and F = {3, 4, 5, 6}
∴ D ∩ F = {3}
Here, F = {3, 4, 5, 6} and S = {1, 2, 3, 4, 5, 6}
∴ F¯=S-F={1,2}
Q5.
Answer :
When three coins are tossed, the sample space is given by
S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
(i) The two events that are mutually exclusive are as follows:
A: getting no heads
B: getting no tails
This is because sets A = {HHH} and B = {TTT} are disjoint.
(ii) The three events that are mutually exclusive and exhaustive are as follows:
A: getting no heads
B: getting exactly one head
C: getting at least two heads
i.e. A = {TTT}, B = {HTT, THT, TTH} and C = {HHH, HHT, HTH, THH}
This is because A ∩ B = B ∩ C = C ∩ A = Φ and A ∪ B ∪ C = S
(iii) The two events that are not mutually exclusive a
A: getting three heads
B: getting at least 2 heads
i.e. A = {HHH} and B = {HHH, HHT, HTH, THH}
This is because A ∩ B = {HHH} ≠ Φ
(iv) The two events which are mutually exclusive but not exhaustive are as follows:
A: getting exactly one head
B: getting exactly one tail
i.e. A = {HTT, THT, TTH} and B = {HHT, HTH, THH}
It is because, A ∩ B = Φ, but A ∪ B ≠ S
Page No.33.18 Ex.33.2
Q6.
Answer :
When a dice is thrown twice, we have the following possible outcomes:
A = both numbers are odd
= {(1, 1), (1, 3),(1, 5), (3, 1), (3, 3), (3, 5), (5, 1), (5, 3), (5, 5)}
B = both numbers are even
= {(2, 2), (2, 4), (2, 6), (4, 2), (4, 4), (4, 6), (6, 2), (6, 4), (6, 6)}
C = sum of the numbers is less than 6
= {(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (4, 1)}
Now, we have:
(A ∪ B) = {(1, 1), (1, 3), (1, 5) ,(3, 1), (3, 3), (3, 5), (5, 1), (5, 3), (5, 5),
(2, 2), (2, 4), (2, 6), (4, 2), (4, 4), (4, 6), (6, 2), (6, 4), (6, 6)}
(A ∩ B) = Φ
(A ∪ C) = {(1, 1), (1, 3),(1, 5), (3, 1), (3, 3), (3, 5), (5, 1), (5, 3), (5, 5),
(1, 2), (1, 4), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (4, 1)}
(A ∩ C) = {(1, 1), (1, 3), (3, 1)}
Since (A ∩ B) = Φ and (A ∩ C) ≠ Φ, A and B are mutually exclusive, but A and C are not.
Q7.
Answer :
When two dices are thrown, there are 62 = 36 possible outcomes.
A = Getting an even number on the first dice
= {(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6),
(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6) }
B = Getting an odd number on the first dice
= {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (3, 1), (3, 2), (3, 3),
(3, 4), (3, 5), (3, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6) }
C = Getting at most 5 as the sum of the numbers on the two dices.
= {(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (4, 1)}
D = Getting a sum greater than 5 but less than 10
= {(1, 5), (1, 6), (2, 4), (2, 5), (2, 6), (3, 3), (3, 4), (3, 5), (3, 6),
(4, 2), (4, 3), (4, 4), (4, 5), (5, 1), (5, 2), (5, 3), (5, 4), (6, 1), (6, 2), (6, 3)}
E = Getting at least 10 as the sum of the numbers on the dices
= {(4, 6), (5, 5), (5, 6), (6, 4), (6, 5), (6, 6)}
F = Getting an odd number on one of the dices
= {(1, 2), (1, 4), (1, 6), (2, 1), (2, 3), (2, 5), (3, 2), (3, 4), (3, 6),
(4, 1), (4, 3), (4, 5), (5, 2), (5, 4), (5, 6), (6, 1), (6, 3), (6, 5)}
Now,
(i)
A and B = A ∩ B = Φ
B or C = B ∪ C
= {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3),
(3, 4), (3, 5), (3, 6), (4, 1), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6) }
B and C = B ∩ C
= {(1, 1), (1, 2), (1, 3), (1, 4), (3, 1), (3, 2)}
A and E = A ∩ E
= {(4, 6), (6, 4), (6, 5), (5, 6), (6, 6)}
A or F = A ∪ F
= {(1, 2), (1, 4), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 2), (3, 4), (3, 6),
(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 2), (5, 4), (5, 6), (6, 1), (6, 2),
(6, 3), (6, 4), (6, 5), (6, 6) }
A and F = A ∩ F
= {(2, 1), (2, 3), (2, 5), (4, 1), (4, 3), (4, 5), (6, 1), (6, 3), (6, 5)}
(ii)
(a) True, because A ∩ B = Φ
(b) True, because A ∩ B = Φ and A ∪ B = S
(c) False, because A ∩ C ≠ Φ
(d) False, because C ∩ D = Φ but C ∪ D ≠ S
(e) True, because C ∩ D ∩ E = Φ and C ∪ D ∪ E = S
(f) True, because A’ ∩ B’ = Φ
(g) False, because A ∩ B ∩ F ≠ Φ and A ∪ B ∪ F = S
Q8.
Answer :
Four slips marked as 1, 2, 3 and 4 are in a box. Two slips are drawn from it one after the other without replacement. The sample space S for the experiment is
S = {(1, 2), (1, 3), (1, 4), (2, 1), (2, 3), (2, 4), (3, 1), (3, 2), (3, 4), (4, 1), (4, 2), (4, 3)}
(i) A = number on the first slip is larger than the one on the second slip
= {(2, 1), (3, 1), (3, 2), (4, 1), (4, 2), (4, 3)}
(ii) B = number on the second slip is greater than 2
={(1, 3), (2, 3), (1, 4), (2, 4), (3, 4), (4, 3)}
(iii) C = sum of the numbers on the two slips is 6 or 7
={(2, 4), (3, 4), (4, 2), (4, 3)}
(iv) D = number on the second slip is two times the number on the first slip
= {(1, 2), (2, 4)}
Clearly, (A ∩ D) = Φ
Therefore, A and D are mutually exclusive events.
Page No.33.44 Ex.33.3
Q1.
Answer :
The sample space of the given experiment is given by
S = {1, 2, 3, 4, 5, 6}
∴ n (S) = 6
(i) Let A be the event of occurrence of a prime number.
Then A = {2, 3, 5}
i.e. n (A) = 3
∴PA=Number of outcomes favourable to ATotal number of possible outcomes=nAnS=36=12
(ii) Let B be the event of occurrence of the number 2 or 4.
Then B = {2,4}
i.e. n (B) = 2
∴PB=Number of outcomes favourable to BTotal number of possible outcomes=nBnS=26=13
(iii) Let C be the event of occurrence of a multiple of 2 or 3.
Then C = {2, 3, 4, 6}
i.e. n (C) = 4
∴PC=Number of outcomes favourable to CTotal number of possible outcomes=nCnS=46=23
Q2.
Answer :
We know that in a single throw of two dices, the total number of possible outcomes is (6 × 6) = 36.
Let S be the sample space.
Then n(S) = 36
(i) Let E1 = event of getting 8 as the sum.
Then E1 = {(2, 6), (3, 5), (4, 4), (5, 3), (6, 2)}
i.e. n (E1) = 5
∴PE1=nE1nS=536
(ii) Let E2 = event of getting a doublet
Then E2 = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)}
i.e. n (E2) = 6
∴PE2=nE2nS=636=16
(iii) Let E3 = event of getting a doublet of prime numbers
Then E3 = {(2, 2), (3, 3), (5, 5)}
i.e. n (E3) = 3
∴PE3=nE3nS=336=112
(iv) Let E4 = event of getting a doublet of odd numbers
Then E4 = {(1, 1), (3, 3), (5, 5)}
i.e. n (E4) = 3
∴PE4=nE4nS=336=112
(v) Let E5 = event of getting a sum greater than 9
Then E5 = {(4, 6), (5, 5), (5, 6), (6, 4), (6, 5), (6, 6)}
i.e. n (E5) = 6
∴PE5=nE5nS=636=16
(vi) Let E6 = event of getting an even number on the first throw
Then E6 = {(2, 1) , (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (4, 1) , (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (6, 1) , (6, 2), (6, 3),
(6, 4), (6, 5), (6, 6) }
i.e. n (E6) = 18
∴PE6=nE6nS=1836=12
(vii) Let E7 = event of getting an even number on one dice and a multiple of 3 on the other
Then E7 = {(2, 3), (2, 6), (4, 3), (4, 6), (6, 3), (6, 6) , (3, 2), (6, 2), (3, 4), (6, 4), (3, 6)}
i.e. n (E7) = 11
∴PE7=nE7nS=1136
(viii) Let E8 = event of getting neither 9 nor 11 as the sum of the numbers on the faces
Then E8¯ = event of getting either 9 or 11 as the sum
Thus, E8 = {(3, 6), (4, 5), (5, 4) , (5, 6), (6, 3), (6, 5) }
i.e. nE8¯=6
∴PE8¯=nE8¯nS=636=16
Hence, PE8=1-PE8¯
=1-16=56
(ix) Let E9 = event of getting a sum less than 6
Then E9 = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (4, 1)}
i.e. n (E9) = 10
∴PE9=nE9nS=1036=518
(x) Let E10 = event of getting a sum less than 7
Then E10 = {(1, 1) , (1, 2), (1, 3), (1, 4), (1, 5), (2, 1) , (2, 2), (2, 3), (2, 4), (3, 1) , (3, 2), (3, 3), (4, 1) , (4, 2), (5, 1)}
i.e. n (E10) = 15
∴PE10=nE10nS=1536=512
(xi) Let E11 = event of getting a sum greater than 7
Then E11 = {(2, 6), (3, 5), (3, 6), (4, 4), (4, 5), (4, 6), (5, 3), (5, 4), (5, 5), (5, 6), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
i.e. n (E11) = 15
∴PE11=nE11nS=1536=512
(xii) Let E12 = event of getting neither a doublet nor a total of 10
Thus E12¯ = event of getting either a doublet or a total of 10
Then E12¯ = {(1, 1), (2, 2), (3, 3), (4, 4), (4, 6), (5, 5), (6, 4), (6, 6)}
i.e. nE12¯=8
∴PE12¯=nE12¯nS=836=29
Hence, PE12=1-PE12¯
= 1 – 29=79
(xiii) Let E13 = event of getting an odd number on the first throw and 6 on the second
Then E13 = {(1,6), (3, 6), (5, 6)}
i.e. n (E13) = 3
∴PE13=nE13nS=336=112
(xiv) Let E14 = event of getting a number greater than 4 on each dice
Then E14 = {(5, 5), (5, 6), (6, 5), (6, 6)}
i.e. n (E14) = 4
∴PE14=nE14nS=436=19
(xv) Let E15 = event of getting a total of 9 or 11
Then E15 = {(3, 6), (4, 5), (5, 4) , (5, 6), (6, 3), (6, 5) }
i.e. n (E15) = 6
∴PE15=nE15nS=636=16
(xvi) Let E16 = event of getting a total greater than 8
Then E16 = {(3, 6), (4, 5), (4, 6), (5, 4), (5, 5), (5, 6), (6, 3), (6, 4), (6, 5), (6, 6)}
i.e. n (E16) = 10
∴PE16=nE16nS=1036=518
Q3.
Answer :
If three dices are thrown simultaneously, then all the possible outcomes = 63 = 216
∴ Total number of possible outcome, n(S) = 216
Let A = event of getting a sum of numbers on three dice as 17 or 18
Then the favourable outcomes are given as
A = {(6, 6, 5), (6, 5, 6), (5, 6, 6), (6, 6, 6)}
Number of favourable outcomes, n(A) = 4
Hence, required probability, P(A) = P (sum of the numbers on three dices as 17 or 18) = 4216=154
Q4.
Answer :
When three coins are tossed once, the sample space is given by
S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
i.e. n (S) = 8
(i) Let E1 = event of getting exactly two heads
Then E1 = {HHT, HTH, THH}
i.e. n(E1) = 3
∴PE1=nE1nS=38
(ii) Let E2 = event of getting at least two heads
Then E2 = {HHH, HHT, HTH, THH}
i.e. n (E2) = 4
∴PE2=nE2nS=48=12
(iii) Let E3 = event of getting at least one head and one tail
Then E3 = {HHT, HTH, HTT, THH, THT, TTH}
i.e. n(E3) = 6
∴PE3=nE3nS=68=34
Q5.
Answer :
There are 365 days, i.e. 52 weeks and one day
This one day can be any of the seven days of the week.
∴ P (Sunday) = 17
We know that 52 weeks will have 52 Sundays.
Hence, required probability = P (an ordinary year with 53 Sundays) = 17
Q6.
Answer :
We know that a leap year has 366 days (i.e. 7 × 52 + 2) = 52 weeks and 2 extra days.
The sample space for these two extra days is given by
S = {(Sunday, Monday), (Monday, Tuesday), (Tuesday, Wednesday), (Wednesday, Thursday), (Thursday, Friday), (Friday, Saturday), (Saturday, Sunday)}
There are 7 cases.
i.e. n(S) = 7
Let E be the event in which the leap year has 53 Sundays and 53 Mondays.
Then E = {(Sunday, Monday) }
i.e. n(E) = 1
∴PE=nEnS=17
Hence, the probability in which a leap year has 53 Sundays and 53 Mondays is 17.
Q7.
Answer :
A and B throw a pair of dices.
Then all the possible outcomes = 62 = 36
i.e. total number of possible outcome, n(S) = 36
Consider E = event where A throws 9 and B throws more than 9, i.e. 10, 11 and 12
E = {(4, 6), (5, 5), (5, 6), (6, 4), (6, 5), (6, 6)}
i.e. n(E) = 6
Hence, required probability = 636=16
Q8.
Answer :
If three dices are thrown simultaneously, then all the possible outcomes = 63 = 216
∴ Total number of possible outcome, n(S) = 216
Let A be the event of getting the same number on all the three dices.
Then, the favourable outcomes are as follows:
A = {(1, 1, 1), (2, 2, 2), (3, 3, 3), (4, 4, 4), (5, 5, 5), (6, 6 , 6)}
Number of favourable outcomes, n(A) = 6
Hence, required probability, P(A) = P (same number on all the three dices) = 6216=136
Q9.
Answer :
If two dices are thrown simultaneously, then all the possible outcomes = 62 = 36
∴ Total number of possible outcome, n(S) = 36
Let A = event where the the total of the numbers on the dices is greater than 10
Then the favourable outcomes are as follows:
A = {(5, 6), (6, 5), (6, 6)}
Number of favourable outcomes, n(A) = 3
Hence, required probability, P(A) = P (total of the numbers on the dices is greater than 10) = 336=112
Page No.33.45 Ex.33.3
Q10.
Answer :
Let S denote the sample space.
Then, n(S) = 52
(i) Let E1 = event of drawing a black king
We know that the number of black kings is two: one for spade and one for club.
i.e. n (E1) = 2
∴PE1=nE1nS=252=126
(ii) Let E2 = event of drawing either a black card or a king
There are 26 black cards including two black kings and there are two more kings.
Therefore, there are 28 cards in which there is a black card or a king.
i.e. n (E2) = 28
∴PE2=nE2nS=2852=713
(iii) Let E3 = event of drawing black and a king
There are two cards: a black card and a king, i.e. a black king.
i.e. n (E3) = 2C1 = 2
∴PE3=nE3nS=252=126
(iv) Let E4 = event of drawing a jack, a queen or a king
Out of 52 cards, there are four jacks, four queens and four kings.
i.e. n (E4) = 4C1 + 4C1 + 4C1
= 4 + 4 + 4 = 12
∴PE4=nE4nS=1252=313
(v) Let E5 = event of drawing neither a heart nor a king
Then E5¯ = event of drawing either a heart or a king
There are 13 cards of heart including one king. Also, there are 3 more kings.
Therefore, out of these 16 cards, one can draw either a heart or a king in 16C1 ways.
i.e. nE5¯=16
∴PE5¯=nE5¯nS=1652=413
∴PE5=1-PE5¯
=1-413=913
(vi) Let E6 = event of drawing a spade or an ace
There are 13 spade cards including one ace. Also, there are 3 more ace cards.
Therefore, out of these 16 cards, one can draw either a spade or an ace in 16C1 ways.
i.e. n (E6) = 16
∴ PE6=nE6nS=1652=413
(vii) Let E7 = event of drawing neither an ace nor a king
Then E7¯ = event of drawing either an ace or a king
There are four ace cards and four king cards.
Therefore, out of these 8 cards, one can draw either an ace or a king in 8C1 ways.
i.e. nE7¯=8
∴PE7¯=nE7¯nS=852=213
∴PE7=1-PE7¯
=1-213=1113
(viii) Let E8 = event of drawing a diamond card.
There are 13 diamond cards in a pack of 52 cards, out of which one diamond can be drawn in 13C1 .
∴ n (E8) = 13
PE8=nE8nS=1352=14
(ix) Let E9 = event of not drawing a diamond card
Then E9¯ = event of drawing a diamond card
There are 13 diamond cards in a pack of 52 cards, out of which one diamond card can be drawn in 13C1.
i.e. nE9¯=1352=14
∴PE9=1-PE9
=1-14=34
(x) Let E10 = event of drawing a black card
We know that there are 26 black cards, i.e. 13 spades and 13 clubs.
Then n (E10) = 26
∴PE10=nE10nS=2652=12
(xi) Let E11 = event of drawing a card which is not an ace
Then E11¯ = event of drawing an ace card
There are four aces in a pack of 52 cards, out of which one ace can be drawn in 4C1 ways.
i.e. nE11=4
∴PE11=nE11nS=113
Hence, PE11=1-PE11
=1-113=1213
(xii)
Let E12 = event of drawing a non-black card
We know that there are 26 non-black cards, i.e. 13 diamonds and 13 hearts.
Then n (E12) = 26
∴PE12=nE12nS=2652=12
Q11.
Answer :
It is given that from a well-shuffled pack of cards, four cards are missing out.
∴ Total number of elementary events, n(S) = 52C4
Let E be the event where four cards are missing from each suit.
i.e. n(E)= 13C1 × 13C1 × 13C1 × 13C1
Hence, required probability = nEnS=C113×C113×C113×C113C452
=13×13×13×1352×51×50×494×3×2×1=13×13×13×1313×17×25×49=219720825
Q12.
Answer :
Four cards can be drawn from a pack of 52 cards in 52C4 ways.
i.e. n(S) = 52C4
Of these, there are four ways to draw all the four honours of a suit, i.e. J, Q, K and A of Spades, Hearts, Diamonds or Clubs.
Let E be the favourable event of that all the four cards drawn are honour cards from the same suit.
Favourable number of events, n(E) = 4C4 or 4C4 or 4C4 or 4C4 = 4C4 + 4C4 + 4C4 + 4C4
Hence, required probability = nEnS=C44+C44+C44+C44C452
=452×51×50×494×3×2×1=413×17×25×49=4270725
Q13.
Answer :
Total number of elementary events, n(S) = 20C1 = 20
Multiples of 3 or 7 = 3, 6, 9, 12, 15, 18, 7, 14
Thus, favourable number of events, n(E) = 8C1 = 8
Hence, required probability = nEnS=820=25
Q14.
Answer :
Total number of balls = 6 + 4 + 8 = 18
Total number of elementary events, n(S) = 18C3
Let E be the event of favourable outcomes.
Here, E = getting one red, one white and one blue ball
So, favourable number of elementary events, n(E) = 6C1 ×4C1 × 8C1
Hence, required probability = nEnS=C16×C14×C18C318
=6×4×818×17×163×2=6×4×86×17×8=417
Q15.
Answer :
Out of 16 balls, two balls can be drawn in 16C2 ways.
∴ Total number of elementary events = 16C2 = 120
(i)
Out of seven white balls, two white balls can be chosen in 7C2 ways.
∴ Favourable number of ways = 7C2
Hence, required probability = C27C216=21120=740
(ii)
Out of five black balls, one black ball can be drawn in 5C1 ways.
Out of four red balls, one red ball can be drawn in 4C1 ways.
Therefore, one black and one red balls can be drawn in 5C1× 4C1 ways.
∴ Favourable number of ways = 5C1× 4C1 = 5× 4 = 20
Hence, required probability = 20120=16
(iii)
‘Two balls drawn are of the same colour’ means that both are either white or black or red.
Out of seven white balls, two white balls can be drawn in 7C2 ways.
Similarly, two black balls can be drawn from five black balls in 5C2 ways and two red balls can be drawn from four red balls in 4C2 ways.
Therefore, number of ways of drawing two balls of the same colour = 7C2 + 5C2 + 4C2 = 21 + 10 + 6 = 37
i.e. favourable number of ways = 37
Hence, required probability = 37120
Q16.
Answer :
Out of 18 balls, three balls can be drawn in 18C3 ways.
∴ Total number of elementary events = 18C3 = 816
(i)
Out of six red balls, one red ball can be drawn in 6C1 ways.
Out of four white balls, two white balls can be drawn in 4C2 ways .
Therefore, one red and two white balls can be drawn in 6C1 × 4C2 = 6 × 6 = 36 ways
∴ Favourable number of ways = 36
Hence, required probability = 36816=368
(ii)
Out of eight blue balls, two blue balls can be drawn in 8C2 ways.
Out of six red balls, one red ball can be drawn in 6C1 ways .
Therefore, two blue and one red balls can be drawn in 8C2 × 6C1 = 28 × 6 = 168 ways
∴ Favourable number of ways = 168
Hence, required probability = 168816=734
(iii)
There are six red balls out of which one red ball can be drawn in 6C1 ways.
Two balls from the remaining 12 balls can be drawn in 12C2 ways.
Therefore, one red two other coloured balls can be drawn in 6C1× 12C2 = 6 × 66 = 396 ways
∴ Favourable number of ways = 396
Hence, required probability = 396816=3368
Q17.
Answer :
Let S denote the sample space.
Then n(S) = 52
Thus, five cards can be drawn in 52C5 ways.
∴ Total number of elementary events = 52C5
(i)
Let E1 = event of getting just one ace
i.e. E1 = 4C1 × 48C4
∴ Total number of favourable events = 4C1 × 48C4
Hence, required probability = C14×C448C552
=4×2×47×46×4552×51×10×49×2
=47×46×913×51×2×49
=47×23×313×17×49=324310829
(ii)
Probability for at least one ace = 1 – Probability (no ace)
= 1-C548C552
= 1-3567354145=1847254145
Q18.
Answer :
Having removed 12 face cards, the remaining 40 cards include 10 cards in each suit.
∴ Chance of drawing a card in the first draw = C140C140=1
Having drawn 1 card, there remain 39 cards of which 30 are of suits different from the drawn card.
∴ Chance of drawing a card of different suit in the second draw = C130C139=3039
Having drawn two cards, there remain 38 cards of which 20 are of suits different from the drawn cards.
∴ Chance of drawing a card of in the third draw = C120C138=2038=1019
Having drawn three cards, there remain 37 cards of which 10 are of suits different from the drawn cards.
∴ Chance of drawing a card in the fourth draw = C110C137=1037
Hence, all the events being dependent, the required probability = 1×3039×1019×1037=10009139
Q19.
Answer :
In a hand at whist, the specified players have 13 cards including fourkings.
Four kings can be drawn out of four in 4C4 ways.
The remaining nine cards held by him can be drawn out of the remaining 48 cards in the pack in 48C9 ways.
The total number of ways in which four kings and nine other cards can be drawn is 4C4× 48C9.
Favourable number of cases = 4C4× 48C9
Also, exhaustive number of cases = 52C13
∴ Required probability = C44×C948C1352=114165
Q20.
Answer :
Out of 100 bulbs, 10 can be chosen in 100C10 ways.
So, total number of elementary events = 100C10
(i)
There are 20 defective and 80 non-defective bulbs.
The number of ways of selecting 10 defective bulbs out of 20 is 20C10 ways.
∴ Favourable number of elementary events = 20C10 ways
Hence, required probability = C1020C10100
(ii)
The number of ways of selecting 10 non-defective bulb out of 80 is 80C10 ways.
∴ Favourable number of elementary events = 80C10
Hence, required probability = C1080C10100
(iii)
Probability for at least one defective bulb = 1 – Probability (all 10 are non-defective)
= 1-C1080C10100
(iv)
‘None is defective’ means that all are non-defective bulbs. The number of ways of selecting all 10 non-defective bulbs out
of 80 is 80C10 ways.
∴ Favourable number of elementary events = 80C10
Hence, required probability = C1080C10100
Q21.
Answer :
There are six letters in the word ‘SOCIAL’, which can be arranged in 6! ways.
There are three vowels, namely O, I and A.
Let us consider these three vowels as one letter.
So, when the three vowels are clubbed together, we have (O, I, A) SCL. We can arrange four letters in a row in 4! ways.
Also, the three vowels can themselves be arranged in 3! ways.
Hence, required probability = 4!×3!6!=4!×3×26×5×4!=15
Q22.
Answer :
There are 7 letters in the word ‘CLIFTON’, which can be arranged in 7! ways.
There are two vowels, namely I and O.
Let us consider these two vowels as one letter.
So, when the two vowels are clubbed together, we have (I,O) CLFTN.
We can arrange six letters in a row in 6! ways.
Also, the two vowels can be arranged in 2! ways.
Hence, required probability = 6!×2!7!=6!×27×6!=27
Q23.
Answer :
There are 10 letters in the word ‘FORTUNATES’, which can be arranged in 10! ways.
There are two T’s in the word.
Let us consider these two letters in the word ‘FORTUNATES’ as one letter.
So, when the two T’s are clubbed together, we have (T,T) FORUNAES.
We can arrange 9 letters in a row in 9! ways.
Also, the two T’s can themselves be arranged in 2! ways.
Hence, required probability = 9!×2!10!=9!×210×9!=15
Q24.
Answer :
Out of the letters in the word ‘UNIVERSITY’, there are two I’s.
Number of permutations = 10!2
The number of words in which two I’s are never together is given by
total number of words – number of words in which two I’s are together.
=10!2-9!=10!-2×9!2=9!10-22=9!×82=9!×4
∴ Required probability = 9!×410!2=9!×4×210×9!=810=45
Q25.
Answer :
If odds in favour of an event A are a : b, then probability of happening of event A = P(A) = aa+b
It is given that the odds in favour of an event are 2 : 3.
Thus, n(S) = 2k + 3k = 5k and n(E) = 2k
Hence, probability of occurrence of this event = nEnS=2k5k=25
Q26.
Answer :
If the odds against the happening of an event A are a : b, then the probability of not happening of event A = PA¯=aa+b
It is given that odds against an event are 7 : 9.
Thus, n(S) = 7k + 9k = 16k
and n(E) = 7k
Hence, probability of non-occurrence of this event = nEnS=7k16k=716
Page No.33.46 Ex.33.3
Q27.
Answer :
Out of 14 balls, two balls can be chosen in 14C2 ways.
So, favourable number of elementary events = 14C2
Let A be the event of getting two balls of different colours.
∴ P(A) = P(1 white and 1 red) + P(1 white and 1 green) + P(1 white and 1 black) + P(1 red and 1 green)
+ P(1 red and 1 black) + P(1 green and 1 black)
⇒PA=C2,1C3,1C14,2+C2,1C5,1C14,2+C2,1C4,1C14,2+C3,1C5,1C14,2+C3,1C4,1C14,2+C5,1C4,1C14,2
=2×391+2×591+2×491+3×591+3×491+5×491
=6+10+8+15+12+2091=7191=0.78
Q28.
Answer :
We know that in a single throw of two dices, the total number of possible outcomes is (6 × 6) = 36.
Let S be the sample space.
Then n(S) = 36
(i)
Let E1 = event of getting neither a doublet nor a total of 8
Then E1′ = event of getting either a doublet or a total of 8
∴ E1′ = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6), (2, 6), (3, 5), (5, 3), (6, 2)}
i.e. n(E1′) = 10
Thus, P(E1′) = 1036
Hence, required probability P(E1) = 1 – P(E1′)
=1-1036=36-1036=2636=1318
(ii)
Let E2 be the event of getting the sum of the numbers obtained on the two dice is neither a multiple of 2 nor a multiple of 3. Then,
E2′ = event of getting the sum of the numbers obtained on the two dice is either a multiple of 2 or a multiple of 3.
∴ E2′ = {(1,1), (1,2), (2, 1), (1, 3), (2, 2), (3, 1), (1, 5), (2, 4), (3, 3), (4, 2), (5, 1), (2, 6), (3, 5), (4, 4), (5, 3), (6, 2), (3, 6),
(4, 5), (5, 4), (6, 3), (4, 6), (5, 5), (6, 4), (6, 6)}
i.e. n(E2′) = 24
Thus, P(E2′) = 2436=23
Hence, required probability P(E2) = 1- P(E2′)
=1-23=3-23=13
Q29.
Answer :
Out of 20 balls, three balls can be drawn in 20C3 ways.
∴ Total number of elementary events = 20C3
(i)
Out of nine blue balls, three blue balls can be chosen in 9C3 ways.
∴ Favourable number of events = 9C3 ways.
Hence, required probability = C39C320=9×8×720×19×18=795
(ii)
Out of eight red balls, one red ball can be drawn in 8C1 ways.
Out of three white balls, one white ball can be drawn in 3C1.
Out of nine blue balls, one blue ball can be drawn in 9C1 ways.
So, favourable number of elementary events = 8C1 × 3C1 × 9C1
Hence, required probability = C18×C13×C19C320=8×3×960×19=1895
Q30.
Answer :
There are 18 balls in the bag out of which two balls can be drawn in 18C2 ways.
So, total number of elementary events = 18C2 = 153
According to the question, both the balls drwan are either red or black, which means that the two balls should be of the same colour.
Out of five red balls, two red balls can be drawn in 5C2 ways.
Similarly, two black balls can be drawn from seven black balls in 7C2 ways.
So, favourable number of elementary events = 5C2 + 7C2 = 10 + 21 = 31
Hence, required probability = 31153
Q31.
Answer :
We know that there are 26 letters in the English alphabet.
So, total number of elementary events, n(S) = 26
(i)
Out of the five vowels of the English alphabet (a, e, i, o, u), one vowel can be chosen in 5C1 ways.
So, favourable number of events = 5C1 = 5
Hence, required probability = 526
(ii)
Out of the 21 consonants of the English alphabet, one consonant can be chosen in 21C1 ways.
So, favourable number of events = 21C1 = 21
Hence, required probability = 2126
Q32.
Answer :
Total number of ways in which one can choose six different numbers from 1 to 20 = 20C6
∴ Total number of elementary events = 20C6 = 38760
Hence, there are 38760 combinations of 6 numbers.
Out of these combinations, one is already fixed by the lottery committee.
Favourable number of elementary events = 1
∴ Required probability = 138760
Q33.
Answer :
Clearly, the sample space is given by S = {1, 2, 3, 4, 5……..19, 20}.
i.e. n(S) = 20
(i)
Let E1 = event of getting a multiple of 4
Then E1 = {4, 8, 12, 16, 20}
i.e. n(E1) = 5
Hence, required probability = P(E1) = nE1nS=520=14
(ii)
Let E2 = event of getting a non-multiple of 4
Then P(non-multiple of 4) = P(E2) = 1 – P(multiple of 4)
= 1-14=34
(iii)
Let E3 = event of getting an odd number
Then E3 = {1, 3, 5, 7, 9, 11, 13, 15, 17, 19}
i.e. n(E3) = 10
Hence, required probability = P(E3) = 1020=12
(iv)
Let E4 = event of getting a number greater than 12
Then E4 = {13, 14, 15, 16, 17, 18, 19, 20}
i.e. n(E4) = 8
Hence, required probability = P(E4) = 820=25
(v)
Let E5 = event of getting a number divisible by 5
Then E5 = {5, 10, 15, 20}
i.e. n(E5) = 4
Hence, required probability = P(E5) = 420=15
(vi)
Let E6 = event of getting a number which is not a multiple of 6
Then E6′ = event of getting a number which is a multiple of 6
E6′ = {6, 12, 18}
i.e. n(E6′ ) = 3
Now, P(E6′) = 320
Hence, required probability P(E6) = 1 − P(E6′)
= 1-320=20-320=1720
Q34.
Answer :
(i)
Let A be the event of ‘getting the sum 4’.
Then A= {(1, 3), (3, 1), (2, 2)}
Here, there are three favourable outcomes, while there are (36 – 3 =) 33 unfavourable outcomes.
∴ Odds in favour of the sum 4 = 333=111 = 1:11
(ii)
Let A be the event of ‘getting the sum 5’.
Then A= {(1, 4), (4, 1), (2, 3), (3, 2)}
Here, there are four favourable outcomes, while there are (36 – 4 =) 32 unfavourable outcomes.
∴ Odds in favour of the sum 5 = 432=18=1:8
(iii)
Let A be the event of ‘getting the sum 6.
Then A= {(1, 5), (5, 1), (2, 4), (4, 2), (3, 3)}
Here, there are five favourable outcomes, while there (36 – 5 =) 31 unfavourable outcomes.
∴ Odds against getting the sum 6 = 315=31:5
Q35.
Answer :
In a pack of 52 cards, there are 13 cards of spade.
There are 13 outcomes favourable to the event ‘a spade’, while the other (52 – 13 =) 39 are unfavourable.
∴ Odds in favour of getting a spade = Number of favourable outcomesNumber of unfavourable outcomes=1339=13=1:3
Again, there are four kings in a pack of 52 cards.
There are 4 outcomes favourable to the event ‘a king’, while the other (52 – 4 =) 48 are unfavourable.
∴ Odds in favour of getting a king = Number of favourable outcomesNumber of unfavourable outcomes=448=112=1:12
Q36.
Answer :
Out of 60 marbles, five marbles can be drawn in 60C5 ways.
∴ Total number of elementary events = 60C5
(i)
Out of 20 blue marbles, five blue marbles can be chosen in 20C5 ways.
∴ Favourable number of events = 20C5 ways
Hence, the required probability is given by
C520C560=20×19×18×17×1660×59×58×57×56=19×6×1759×29×57×7=2×1759×29×7=3411977
(ii) P (no green) = Favourable outcomes Total outcomes
= 30C560C5
Thus, P(at least one green) = 1 – P (no green)
=1-C530C560=1-1174484=4484-1174484=43674484
Q37.
Answer :
Total number of marbles = (6 + 4) = 10
Let S be the sample space.
Then n(S) = number of ways of selecting one marble out of 10 = 10C1 = 10 ways
(i)
Let E1 = event of getting a white marble
∴ n(E1) = 4C1 = 4
Hence, required probability = C14C110=410=25
(ii)
Let E2 = event of getting a white marble, which is odd numbered.
i.e. E2 = {13, 15}
∴ n(E2) = 2
Hence, required probability = nE2nS=210=15
(iii)
Let E3 = event of getting an even numbered marble
i.e. E3 = {2, 4, 6, 12, 14}
∴ n(E3) = 5
Hence, required probability = nE3nS=510=12
(iv)
Let E4 = event of getting a red marble
i.e. E4 = {1, 2, 3, 4, 5, 6}
∴ n(E4) = 6
Now, P(E4) = 610=35 …(i)
Let E5 = event of getting even numbered marble
Then E5 = {2, 4, 6, 12, 14}
i.e.n(E5) = 5
Now, P(E5) = 510=12 …(ii)
From (i) and (ii), we get:
E4 ∩ E5 = {2, 4, 6}
⇒n(E4 ∩ E5) = 3
⇒P(E4 ∩ E5) = 310
By addition theorem, we have:
P (E4 ∪ E5) = P(E4) + P (E5) − P (E4 ∩ E5)
⇒ P (E4 ∪ E5) = 35+12-310=810=45
Hence, required probability = P(E4 ∪ E5) = 45
Q38.
Answer :
Total number of students = (10 + 8) = 18
Let S be the sample space.
Then n(S) = number of ways of selecting 3 students out of 18 = 18C3 ways
(i)
Out of 10 boys, three boys can be selected in 10C3 ways.
∴ Favourable number of events, n(E) = 10C3
Hence, required probability = C310C318=10×9×818×17×16=534
(ii)
Out of eight girls, three girls can be selected in 8C3 ways.
∴ Favourable number of events, n(E) = 8C3
Hence, required probability = C38C318=8×7×618×17×16=7102
(iii)
One boy and two girls can be selected in 10C1 × 8C2.
∴ Favourable number of events = 10C1 × 8C2
Hence, required probability = C110×C28C318=10×28816=35102
(iv)
Probability of at least one girl = 1 – P(no girl)
= 1 – P(all 3 are boys)
= 1-C310C318=1-534=2934
(v)
Let E be the event with at most one girl in the group.
Then E = {0 girl, 1 girl}
∴ Favourable number of events, n(E) = 8C0 × 10C3 × 8C1 × 10C2
Hence, the required probability is given by
C08×C310+C18×C210C318=1×C310+ C18×C210C318=1×120+8×45816=480816=1017
Q39.
Answer :
Out of 52 cards from a deck, 5 cards can be drawn in 52C5 ways.
∴ Total number of elementary events = 52C5
Out of 13 cards of heart, 5 cards can be drawn in 13C5 ways.
∴ Favourable number of events = 13C5
Hence, required probability = C513C552=13×12×11×10×952×51×50×49×48=3366640
Q40.
Answer :
Clearly, the sample space is given by S = {1, 2, 3, 4, 5,…19, 20}.
∴ n(S) = 20C2 = 190
(i)
Let E1 be the event where both the tickets have prime numbers on them.
Then E1 = {2, 3, 5, 7, 11, 13, 17, 19}
∴ Favourable number of ways = n(E1) = 8C2
Hence, required probability = P(E1) = nE1nS=C28C220=1495
(ii)
Let E2 be the event where one ticket has a prime number, while the other has a multiple of 4.
Then prime numbers = {2, 3, 5, 7, 11, 13, 17, 19}
and multiples of 4 = {4, 8, 12, 16, 20}
∴ Favourable number of ways, n(E2) = 8C1× 5C1 = 8 × 5 = 40
Hence, required probability, P(E2 ) = nE2nS=40190=419
Q41.
Answer :
Out of 15 balls, two balls can be drawn in 15C2 ways.
∴ Total number of elementary events = 15C2 = 105
(i)
Out of three red balls, two red balls can be chosen in 3C2 ways.
∴ Favourable number of ways = 3C2 = 3
Hence, required probability = 3105=135C27C216=21120=740
(ii)
Out of three red balls, one red ball can be drawn in 3C1 ways; and out of five black balls, one black ball can be drawn in 5C1 ways.
Therefore, one red and one black can be drawn in 3C1× 5C1 ways.
∴ Favourable number of ways = 3C1× 5C1 = 3× 5 = 15
Hence, required probability = 15105=17
(iii)
Out of seven white balls, one white ball can be drawn in 7C1 ways; and one ball can be drawn from the rest of the other coloured (red and black) balls in 8C1 ways.
∴ Favourable number of ways = 7C1× 8C1 = 7× 8 = 56
Hence, required probability = 56105=815
Page No.33.47 Ex.33.3
Q42.
Answer :
(i)
Here, each of the numbers p(ωi) is positive and less than 1.
∴ Sum of probabilities = pω1+pω2+pω3+pω4+pω5+pω6+pω7
= 0. 1 + 0.01 + 0.05 + 0.03 + 0.01 + 0.2 + 0.6 = 1
Thus, the assignment is valid.
(ii)
Here, each of the numbers p(ωi) is positive and less than 1.
∴ Sum of probabilities = pω1+pω2+pω3+pω4+pω5+pω6+pω7
= 17+17+17+17+17+17+17=7×17=1
Thus, the assignment is valid.
(iii)
Here, each of the numbers p(ωi) is positive and less than 1.
∴ Sum of probabilities = pω1+pω2+pω3+pω4+pω5+pω6+pω7
= 0.7 + 0.6 + 0.5 + 0.4 + 0.3 + 0.2 + 0.1
= 2.8 ≠ 1
Thus, the assignment is not valid.
(iv)
Given:
pω7=1514>1
Thus, the assignment is not valid.
Q43.
Answer :
Total number of people = 2 + 2 = 4
Out of these four people, two can be selected in 4C2 = 6 ways.
(i) No man in the committee of two means that there will be two women in the committee.
Out of two women, two can be selected in 2C2 = 1 way.
∴ P(no man) = C22C24=12×3=16
(ii) One man in the committee of two means that there is one woman in the committee.
One man out of 2 can be selected in 2C1 = 2 ways.
One woman out of 2 can be selected in 2C1 = 2 ways.
Together, they can be selected in 2C1 × 2C1 ways.
∴ P (one man) = C12×C12C24=2×22×3=23
(iii) Two men can be selected in 2C2 way.
∴ P (two men) = C22C24=12×3=16
Q44.
Answer :
Out of four men and six women, one person can be chosen in 10C1 = 10 ways.
Number of ways of selecting one women out of six women = 6C1 = 6 ways.
∴Required probability=610=35
Page No.33.65 Ex.33.4
Q1.
Answer :
Given:
P(A) = 0.3, P (B) = 0.4 and P (A ∪ B) = 0.5
By addition theorem, we have:
P (A ∪ B) = P(A) + P (B) – P (A ∩ B)
⇒ 0.5 = 0.3 + 0.4 – P (A ∩ B)
⇒ 0.5 = 0.7 – P (A ∩ B)
⇒ P (A ∩ B) = 0.7 – 0.5
= 0.2
Hence, P (A ∩ B) = 0.2
Page No.33.66 Ex.33.4
Q2.
Answer :
Given:
P(A) = 0.5, P (B) = 0.3 and P (A ∩ B) = 0.2
By addition theorem, we have:
P (A ∪ B) = P(A) + P (B) – P (A ∩ B)
⇒ P (A ∪ B) = 0.5 + 0.3 – 0.2
= 0.8 – 0.2 = 0.6
Hence, P (A ∪ B) = 0.6
Q3.
Answer :
Given:
P (A ∪ B) = 0.8, P (A ∩ B) = 0.3 and PA¯=0.5
We know that
PA+PA¯=1
⇒PA+0.5=1
⇒PA=1-0.5=0.5
By addition theorem, we have:
P (A ∪ B) = P(A) + P (B) -P (A ∩ B)
⇒ 0.8 = 0.5 + P (B) – 0.3
⇒ 0.8 = 0.2 + P (B)
⇒ P (B) = 0.8 – 0.2
= 0.6
Hence, P (B) = 0.6
Q4.
Answer :
Given:
P(A) = 1/2 and P(B) = 1/3
For mutually exclusive events A and B, we have:
P(A or B) = P(A) + P(B)
=12+13=3+26=56
Hence, PA or B=56
Q5.
Answer :
(a)
Given:
P(A) = 0.4 and P(B) = 0.5
If A and B be mutually exclusive event, then P (A ∩ B) = 0
(i)
By addition theorem, we have:
P (A ∪ B) = P(A) + P (B) – P (A ∩ B)
= 0.4 + 0.5 – 0 = 0.9
(ii)
PA¯∩B=1-PA∪B
= 1 – 0.9 = 0.1
(iii)
PA¯∩B=PB-PA∩B
= 0.5 – 0 = 0.5
(iv)
PA∩B¯=PA-PA∩B
= 0.4 – 0 = 0.4
(b)
Given:
P (A) = 0.54, P (B) = 0.69 and P (A ∩ B) = 0.35
(i)
By addition theorem, we have:
P (A ∪ B) = P(A) + P (B) – P (A ∩ B)
= 0.54 + 0.69 – 0.35
= 0.88
(ii)
PA¯∩B=1-PA∪B
= 1 – 0.88
= 0.12
(iii)
PA∩B¯=PA-PA∩B
= 0.54 – 0.35
= 0.19
(iv)
PA¯∩B=PB-PA∩B
= 0.69 – 0.35
= 0.34
(c)
Given:
PA=13,PB=15and PA∩B=115
(i)
By addition theorem, we have:
P (A ∪ B) = P(A) + P (B) – P (A ∩ B)
=13+15-115
=5+3-115=715
(ii)
Given:
P (A) = 0.35, P (A ∪ B) = 0.6 and P (A ∩ B) = 0.25
By addition theorem, we have:
P (A ∪ B) = P(A) + P (B)- P (A ∩ B)
0.6 = 0.35 + P (B) – 0.25
P (B) = 0.6 – 0.35 + 0.25
= 0.6 – 0.1 = 0.5
(iii)
Given:
P (A) = 0.5, P(B) = 0.35 and P (A ∪ B) = 0.7
By addition theorem, we have:
P (A ∪ B) = P(A) + P (B) – P (A ∩ B)
0.7 = 0.5 + 0.35 – P (A ∩ B)
P (A ∩ B) = 0.5 + 0.35 – 0.7
= 0.85 – 0.7 = 0.15
Q6.
Answer :
Since the odds against event A are 8 : 3, the probability of the happening of event A is given by
P(A) = 38+3=311
Similarly, the odds against event B are 5 : 2.
So, P(B) = 25+2=27
Since events A, B and C are such that one of them must and only one can happen, A, B and C are mutually exclusive and totally exhaustive events.
Consequently, A ∪ B ∪ C = S
and A ∩ B = B ∩ C = C ∩ A = Φ
Thus, P (A ∪ B ∪ C) = P(S) = 1
⇒ P(A) + P(B) + P(C) = 1
⇒ 311+27+PC=1
⇒PC=1-311-27=3477
Hence, odds against the events are PC¯:PC=1-3477:3477
= (77 – 34) : 34
= 43 : 34
Q7.
Answer :
Let the given events be A and B
Now, PA=23PB.
Let P(B) = x
∴PA=23x
The events A and B are exhaustive.
∴ P(A) or P(B) = 1
⇒ P(A) + P(B) = 1 (∵ A and B are mutually exclusive)
⇒23x+x=1
⇒5×3=1
⇒x=35
∴PB=35
This implies that the odds in favour of B are 3 : (5 – 2), i.e. 3 : 2.
Q8.
Answer :
If A and B denote the events of drawing a spade card and a king, respectively, then event A consists of 13 sample points, whereas event B consists of four sample points.
Thus, PA=1352 and PB=452
The compound event (A ∩ B) consists of only one sample point, i.e. the king of spade.
So, PA∩B=152
By addition theorem, we have:
P (A ∪ B) = P(A) + P (B)- P (A ∩ B)
= 1352+452-152=13+4-152=1652=413
Hence, the probability that the card drawn is either a spade or a king is given by 413.
Q9.
Answer :
Here, S = {(1, 1), (1, 2)…,(6, 5), (6, 6)}
∴ Number of possible outcomes = 6 × 6 = 36
Let E be the event where a doublet appears and F be the event where the total is 9.
i.e. E = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)}
and F = {(3, 6), (4, 5), (5, 4), (6, 3)}
∴PE=636=16 and PF=436=19
P(neither a doublet nor a total of 9) = PE¯∩F¯=PE∪F¯=1-PE∪F …(i)
The events E and F are mutually exclusive.
By addition theorem, we have:
P (E ∪ F) = P(E) + P (F)
= 16+19=3+218=518
From (i), we get:
PE¯∩F¯=1-518=18-518=1318
Q10.
Answer :
Let S be the sample space.
Then n(S) = 500
∴ Total number of elementary events = 500
Let A be the event where the number selected is divisible by 3 and B be the event where the number selected is divisible by 5.
Then A = {3, 6, 9, 12, 15, …498}
and B = {5, 10, 15, 20, 25, …500}
and (A ∩ B) = { 15, 30, 45, …495}
We have:
nA=4983=166
nB=5005=100
nA∩B=49515=33 [∵ LCM of 3 and 5 is 15]
∴PA=166500, PB=100500 and PA∩B=33500
Now, required probability = P(a number is divisible by 3 or 5)
= P (A ∪ B)
= P(A) + P(B) – P(A ∩ B)
= 166500+100500-33500=266-33500=233500
Q11.
Answer :
Let A be event where the first throw comes up with the number 3.
Also, let B be the event where the second throw comes up with the number 3.
∴ Favourable events of A = {(3, 1),(3, 2), (3, 3), (3, 4), (3, 5), (3, 6)} = 6
⇒PA=636=16
∴ Favourable events of B = {(1, 3), (2, 3), (3, 3), (4, 3),(5, 3), (6, 3) } = 6
⇒PB=636=16
Also, PA∩B=136 [∵ Only one event will be common, i.e. (3, 3)]
Hence, required probability =P(A∪B)
= P(A)+P(B)-P(A∩B)=16+16-136=6+6-136=1136
Q12.
Answer :
If A and B denote the events of drawing an ace and a spade card, respectively, then event A consists of four sample points, whereas event B consists of 13 sample points.
Thus, PA=452 and PB=1352
The compound event (A ∩ B) consists of only one sample point, i.e. an ace of spade.
So, PA∩B=152
By addition theorem, we have:
P (A ∪ B) = P(A) + P (B) – P (A ∩ B)
= 452+1352-152=4+13-152=1652=413
Hence, the probability that the card drawn is either an ace or a spade card is given by 413.
Q13.
Answer :
P(a spade or a king)=P(a spade)+P(a king)-P(a king of spade)=1352+452-152=1652=413
Q14.
Answer :
Let S be the sample space.
Then n(S) = 100
∴ Total number of elementary events = 100
Let A be the event where the number selected is divisible by 4 and B be the event where the number selected is divisible by 6.
Then A = {4, 8, 12, 16, …100 }
B = { 6, 12, 18, 24, …96},
and (A ∩ B) = {12, 24, …96}
Now, we have:
nA=1004=25
nB=966=16
nA∩B=9612=8 [∵ LCM of 4 and 6 is 12]
∴PA=25100, PB=16100 and PA∩B=8100
Now, required probability = P(a number is divisible by 4 or 6)
= P (A ∪ B)
= P(A) + P(B) -P(A ∩ B)
= 25100+16100-8100=25+16-8100=33100
Q15.
Answer :
Out of 52 cards, four cards can be randomly chosen in 52C4 ways.
∴ n(S) = 52C4
Let A = event where the four cards drawn are red
and B = event where the four cards drawn are black
Then, n(A) = 26C4 and n(B) = 26C4
⇒PA=C426C452 and PB=C426C452
A and B are mutually exclusive events.
i.e. P (A ∩ B) = 0
By addition theorem, we have:
P (A ∪ B) = P(A) + P (B) – P (A ∩ B)
= C426C452+C426C452- 0
= 4617×49+4617×49
= 2×4617×49=92833
Hence, the probability that all the drawn cards are of the same colour is 92833.
Q16.
Answer :
Let S be the sample space associated with the experiment of students who appeared for two examination.
Then n(S) = 100
∴ Total number of elementary events = 100
Consider the following events:
A = students passed in first examination
B = students passed in second examination
Then n(A) = 60 and n(B) = 50 and n(A ∩ B) = 30
∴PA=60100, PB=50100 and PA∩B=30100
By addition theorem, we have:
P (A ∪ B) = P(A) + P (B) – P (A ∩ B)
= 50100+60100-30100=50+60-30100=80100=45
Hence, the probability that a student selected at random has passed at least one examination is 45.
Page No.33.67 Ex.33.4
Q17.
Answer :
There are 10 + 6 + 10 = 26 balls in total.
So, the total number of possible outcomes is 26.
Consider the following events:
W = event of drawing a white ball
R = event of drawing a red ball
Then n(W) = 10 and n(R) = 6
Since both the events are mutually exclusive, we have:
(A ∩ B) = 0
∴PA=1026, PB=626 and P (A ∩ B) = 0
By addition theorem, we have:
P (A ∪ B) = P(A) + P (B) -P (A ∩ B)
= 1026+626-0
= 1626=813
Hence, the probability that the ball drawn is either white or red is 813.
Q18.
Answer :
Let Q, R, S and T be the events where horses A, B, C and D win the race, respectively.
Then, P(Q)=14, P(R)=15, PS=16 and PT=17
Since only one horse can win the race, Q, R, S and T are mutually exclusive events.
∴ Required probability = P (Q ∪ R ∪ S ∪ T)
= P(Q) + P(R) + P(S) + P(T)
= 14+15+16+17
= 319420
Q19.
Answer :
We have two events such that
A = a person will travel by plane
and B = a person will travel by train.
i.e. PA=35 and PB=14
Since A and B are mutually exclusive events, we have:
P (A ∩ B) = 0
By addition theorem, we have:
P (A ∪ B) = P(A) + P (B) – P (A ∩ B)
= 35+14-0=12+520=1720
Hence, required probability = 1720
Q20.
Answer :
Let S be the sample space.
Then n(S) = number of ways of drawing two cards out of 52 = 52C2
Let E1 = event in which both the cards are black cards
and E2 = event in which both the cards are kings.
Then (E1∩ E2) = event of getting two black kings
i.e. n(E1) = number of ways of drawing two black cards out of the black cards = 26C2
n(E2) = number of ways of drawing two kings out of four kings = 4C2
∴ n(E1∩ E2) = number of ways of drawing two black kings out of two kings = 2C2 = 1
Thus, PE1=nE1nS=C226C252; PE2=nE2nS=C24C252
and PE1∩E2=nE1∩E2nS=1C252
∴ P(drawing both red cards or both kings) = P(E1or E2)
= P(E1∪ E2)
= P(E1) + P(E2)- P( E1∩ E2)
= C226C252+C24C252-1C252
= C226+C24-1C252
= 326+6+11326=3301326=55221
Hence, the required probability is 55221.
Q21.
Answer :
∵P(2 aces)=452×351=1252×51,P(2 black cards)=2652×2551=26×2552×51and, P(2 black aces)=252×151=252×51∴P(either aces or black cards)=P(2 aces)+P(2 black cards)-P(2 black aces)=1252×51+26×2552×51-252×51=662-252×51=66052×51=5513×17=55221
Q22.
Answer :
The numbers of bolts and nuts are 30 and 40, respectively.
Then the numbers of rusted bolts and rusted nuts are 15 and 20, respectively.
Total number of items = 30 + 40 = 70
Total number of rusted items = 15 + 20 = 35
Total number of ways of drawing two items = 70C2
Let R and B be the events in which both the items drawn are rusted items and bolts, respectively.
R and B are not mutually exclusive events, because there are 15 rusted bolts.
P(items are both rusted or both bolts) = P (R ∪ B)
= P(R) + P (B) -P (R ∩ B)
= C235C270+C230C270-C215C270=1×270×6935×341×2+30×291×2-15×141×2
=185070×69=185483
Q23.
Answer :
Let S be the sample space. Then n(S) = 200
∴ Total number of elementary events = 200
Let A be the event in which the number selected is divisible by 6 and B be the event in which the number selected is divisible by 8.
Then A = {6, 12, 18, 24, …198 },
B = { 8, 16, 24, 32, …200}
and (A ∩ B) = {24, 48, 72, …192}
Now, we have:
nA=1986=33
nB=2008=25
nA∩B=19224=8 [∵ LCM of 6 and 8 is 24]
∴PA=33200, PB=25200 and PA∩B=8200
Now, required probability = P(a number is divisible by 6 or 8)
= P (A ∪ B)
= P(A) + P(B) – P(A ∩ B)
= 33200+25200-8200=33+25-8200=50200=14
Q24.
Answer :
Let S be the sample space associated with the experiment that a coin is tossed four times.
Then n(S) = 24 = 16
Consider the following events:
A: Event of getting 2 tails
B : Event of getting 3 tails
Then A = {HHTT , HTHT, HTTH, THTH, TTHH, THHT}
n(A) = 6
∴PA=616
B = {HTTT, THTT, TTHT, TTTH}
n (B) = 4
∴PB=416
Since events A and B are mutually exclusive, we have:
PA∩B=0
By addition theorem, we have:
P(A ∪ B) = P(A) + P (B) – P (A ∩ B)
= 616+416-0=1016=58
Q25.
Answer :
Let A and B be the events of passing the first and the second examinations, respectively.
Accordingly, P(A) = 0.8, P(B) = 0.7 and P(A or B) = 0.95
We know that
P(A or B) = P(A) + P(B) – P(A and B)
⇒ 0.95 = 0.8 + 0.7 – P(A and B)
⇒ P(A and B) = 0.8 + 0.7 – 0.95
= 1.5 – 0.95 = 0.55
Thus, the probability of passing both the examinations is 0.55.
Q26.
Answer :
Let A and B be the events of passing English and Hindi examinations, respectively.
Accordingly, we have:
P(A and B) = 0.5
P(not A and not B) = 0.1 [i.e. P(A’ ∩ B’) = 0.1]
P(A) = 0.75
Now, P(A∪B) + P(A’ ∩ B’) = 1
⇒ P(A∪B) = 1- P(A’ ∩ B’)
= 1 – 0.1 = 0.9
By addition theorem, we have:
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
⇒ 0.9 = 0.75 + P (B) – 0.5
⇒ P(B) = 0.9 – 0.75 + 0.5
⇒ P(B) = 0.65
Thus, the probability of passing the Hindi examination is 0.65.
Page No.33.68 (Very Short Answers)
Q1.
Answer :
Let S be the sample space associated with three numbers that are chosen at random from the numbers 1 to 30.
∴ n(S) = 30C3 = 30!27!×3!=30×29×28×27!27!×3×2×1=5×29×28=4060
Let E be the favourable number of elementary events that the chosen numbers are consecutive.
E = {(1, 2, 3), (2, 3, 4), (3, 4, 5),…, (27, 28, 29), (28, 29, 30)}
i.e. n(E) = 28C1 = 28
Hence, required probability = PE=nEnS=284060=1145
Q2.
Answer :
It is given that n (≥ 3) persons are seated in a row and two persons are selected.
∴ Total number of elementary event = n(S) = nC2
Let E be the event associated with the experiment that two persons are together.
∴ n(E) = n -1C1
Thus, required probability = P(E) = n(E)n(S)
=C1n-1C2n
=n-1nn-12=2n-1nn-1=2n
Q3.
Answer :
There are 11 letters in the word ‘PROBABILITY’.
i.e. n(S) = 11
There are 4 vowels (O, A, I, I) in the given word.
i.e. n(vowel) = 4
∴ Probability (vowel) = 411
Q4.
Answer :
We know that a leap year has 366 days (i.e. 7 × 52 + 2) = 52 weeks and 2 extra days
The sample space for these two extra days are as follows:
S = {(Sunday, Monday), (Monday, Tuesday), (Tuesday, Wednesday), (Wednesday, Thursday), (Thursday, Friday), (Friday, Saturday), (Saturday, Sunday)}
There are 7 cases.
i.e. n(S) = 7
Let E be the event that a leap year has 53 Fridays or 53 Saturdays.
Then E = { (Thursday, Friday), (Friday, Saturday), (Saturday, Sunday)}
i.e. n(E) = 3
∴PE=nEnS=37
Hence, the probability that a leap year has 53 Fridays or 53 Saturdays is 37.
Q5.
Answer :
If three dices are thrown simultaneously, then the number of all the possible outcomes are 63 = 216.
∴ Total number of possible outcome = n(S) = 216
Let A be the event of getting a sum of 15 when three dices are thrown simultaneously.
The favourable outcomes are as follows:
A = {(3,6 , 6), (4, 6, 5), (5, 6, 4), (6, 6, 3), (6, 3, 6), (6, 4, 5), (6, 5, 4), (4, 5, 6), (5, 5, 5), (5, 4, 6)}
i.e. number of favourable outcomes = n(A) = 10
Hence, required probability = P (getting a sum of 15) = 10216
Page No.33.69 (Very Short Answers)
Q6.
Answer :
There are 11 letters in the word ‘MISSISSIPPI’ which can be arranged in 11! ways.
Number of the letter S = 4
Let us consider the four S’s in the given word as one letter.
So, when the four letters are clubbed together, we have (SSSS) MIIIPPI. We can arrange eight letters in a row in 8! ways.
Also, the four S’s can be arranges in 4! ways.
Hence, required probability = 8!×4!11!=8!×4×3×211×10×9×8!=4×3×211×10×9=4165
Q7.
Answer :
Probability of any chosen month out of 12 months = 112
There are seven possible ways in which a month can start and it will be a Friday on the 13th day if the first day of the month is Sunday.
So, its probability = 17
Thus, required probability = 112×17=184
Hence, the probability that the 13th day of a randomly chosen month is Friday = 184
Q8.
Answer :
We choose three vertices out of 6 in 6C3 = 20 ways.
∴ Total number of elementary events = n(S) = 20
Number of ways of choosing an equilateral triangle = 2
i.e. A1A3A5 or A2A4A6
∴ Total number of favourable events = n(E) = 2
Hence, required probability = 220=110
Q9.
Answer :
PE1∪E2∩E1¯∩E2¯=PE1∩E1¯∩E2¯∪E2∩E1¯∩E2¯
=Pϕ∪ϕ=0
Q10.
Answer :
PA¯∩B=1-PA∪B
⇒PA∪B =1-PA¯∩B=1-13=23
By addition theorem, we have:
P (A ∪ B) = P(A) + P (B) – P (A ∩ B)
∴ P(A) + P (B) = P (A ∪ B) + P (A ∩ B)
= 23+16=4+16=56
Thus, P(A) + P (B) = 56 …(i)
Again, P (A ∩ B) = P(A) × P(A) = 16
By formula, we have:
{P(A) − P (B)}2 = {P(A) + P (B)}2 − 4 × P(A) × P(B)
= 562-46=2536-46=25-2436=136
∴ P(A) − P(B) = 16 …(ii)
From (i) and (ii), we get:
2P(A) = 1
Hence, P(A) = 12 and P(B) = 13
Page No.33.69 (Multiple Choice Questions)
Q1.
Answer :
(c) 4/13
If A and B denote the events of drawing a king and a spade card, respectively, then event A consists of four sample points, whereas event B consists of 13 sample points.
Thus, PA=452 and PB=1352
The compound event (A ∩ B) consists of only one sample point, king of spade.
So, PA∩B=152
By addition theorem , we have:
P (A ∪ B) = P(A) + P (B) − P (A ∩ B)
= 452+1352-152=1652=413
Hence, the probability that the card drawn is either a king or a spade is given by 413
Q2.
Answer :
(b) 3/4
When two dice are thrown, there are (6 × 6) = 36 outcomes.
The set of all these outcomes is the sample space, given by
S = (1, 1) , (1, 2), (1, 3), (1, 4), (1, 5), (1, 6)
(2, 1) , (2, 2), (2, 3), (2, 4), (2, 5), (2, 6)
(3, 1) , (3, 2), (3, 3), (3, 4), (3, 5), (3, 6)
(4, 1) , (4, 2), (4, 3), (4, 4), (4, 5), (4, 6)
(5, 1) , (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)
(6, 1) , (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)
i.e. n(S) = 36
Let E be the event of getting at least one digit greater than 3.
Then E = {(1, 4), (1, 5), (1, 6), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6), (4, 1) , (4, 2), (4, 3), (4, 4), (4, 5), (4, 6),
(5, 1) , (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1) , (6, 2), (6, 3), (6, 4), (6, 5), (6, 6) }
∴ n(E) = 27
Hence, required probability = 2736=34
Q3.
Answer :
(c) 1/9
When two dice are thrown, there are (6 × 6) = 36 outcomes.
The set of all these outcomes is the sample space given by
S = (1, 1) , (1, 2), (1, 3), (1, 4), (1, 5), (1, 6)
(2, 1) , (2, 2), (2, 3), (2, 4), (2, 5), (2, 6)
(3, 1) , (3, 2), (3, 3), (3, 4), (3, 5), (3, 6)
(4, 1) , (4, 2), (4, 3), (4, 4), (4, 5), (4, 6)
(5, 1) , (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)
(6, 1) , (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)
i.e. n(S) = 36
Let E be the event of getting a total score of 5.
Then E = {(1, 4), (2, 3), (3, 2), (4, 1)}
∴ n(E) = 4
Hence, required probability = nEnS=436=19
Q4.
Answer :
(b) 6/36
When two dices are thrown, there are (6 × 6) = 36 outcomes.
The set of all these outcomes is the sample space given by
S = (1, 1) , (1, 2), (1, 3), (1, 4), (1, 5), (1, 6)
(2, 1) , (2, 2), (2, 3), (2, 4), (2, 5), (2, 6)
(3, 1) , (3, 2), (3, 3), (3, 4), (3, 5), (3, 6)
(4, 1) , (4, 2), (4, 3), (4, 4), (4, 5), (4, 6)
(5, 1) , (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)
(6, 1) , (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)
∴ n(S) = 36
Let E be the event of getting a total score of 7.
Then E = {(1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)}
∴ n(E) = 6
Hence, required probability = nEnS=636
Q5.
Answer :
(b) 1/12
When two dices are thrown, there are (6 × 6) = 36 outcomes.
The set of all these outcomes is the sample space, given by
S = (1, 1) , (1, 2), (1, 3), (1, 4), (1, 5), (1, 6)
(2, 1) , (2, 2), (2, 3), (2, 4), (2, 5), (2, 6)
(3, 1) , (3, 2), (3, 3), (3, 4), (3, 5), (3, 6)
(4, 1) , (4, 2), (4, 3), (4, 4), (4, 5), (4, 6)
(5, 1) , (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)
(6, 1) , (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)
i.e. n(S) = 36
Let E be the event of getting a total score of 10.
Then E = {(4, 6), (5, 5), (6, 4)}
∴ n(E) = 3
Hence, required probability = nEnS=336=112
Q6.
Answer :
(c) 1/10
Clearly, the sample space is given by
S = {1, 2, 3, 4, 5… 97, 98, 99, 100}
∴ n(S) = 100
Let E = event of getting a square.
Then E = {1, 4, 9, 16, 25, 36, 49, 64, 81, 100}
∴ n(E) = 10
Hence, required probability = nEnS=10100=110
Q7.
Answer :
(a) 47/66
Out of 12 balls, two balls can be drawn in 12C2 ways.
∴ Total number of elementary events, n(S) = 12C2 = 66
We observe that at least one ball of each colour can be drawn in one of the following mutually exclusive ways:
(i) 1 red and 1 white
(ii) 1 red and 1 blue
(iii) 1 white and 1 blue
Thus, if we define three events A, B and C as follows:
A = drawing 1 red and 1 white
B = drawing 1 red and 1 blue
C = drawing 1 white and 1 blue
then, A, B and C are mutually exclusive events.
∴ Required probability = P(A ∪ B ∪ C)
= P(A) + P(B) + P(C)
= C13×C14C212+C13×C15C212+C14×C15C212
= 3×466+3×566+4×566
= 1266+1566+2056=4766
Q8.
Answer :
(b) 13/18
When two dices are thrown, there are (6 × 6) = 36 outcomes.
The set of all these outcomes is the sample space is given by
S = (1, 1) , (1, 2), (1, 3), (1, 4), (1, 5), (1, 6)
(2, 1) , (2, 2), (2, 3), (2, 4), (2, 5), (2, 6)
(3, 1) , (3, 2), (3, 3), (3, 4), (3, 5), (3, 6)
(4, 1) , (4, 2), (4, 3), (4, 4), (4, 5), (4, 6)
(5, 1) , (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)
(6, 1) , (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)
∴ n(S) = 36
Let E be the event of getting the digits which are neither equal nor give a total of 9.
Then E’ = event of getting either a doublet or a total of 9
Thus, E’ = {{1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6), (3, 6), (4, 5), (5, 4), (6, 3)}
i.e. n(E’) = 10
P(E’) = nE’nS=1036=518
Hence, required probability P(E) = 1- P(E’)
= 1-518=1318
Q9.
Answer :
(c) 10/21
There are nine persons (three men, two women and four children) out of which four persons can be selected in 9C4 = 126 ways.
∴ Total number of elementary events = 126
Exactly two children means selecting two children and two other people from three men and two women.
This can be done in 4C2 × 5C2 ways.
∴ Favourable number of elementary events = 4C2 × 5C2 = 60
So, required probability = 60126=1021
Q10.
Answer :
(a) 0.39
Given:
P(A) = 0.25, P(B) = 0.50 and P(A∩B) = 0.14
∴ Required probability = 1 -P(A∪B)
= 1 – [P(A) + P(B) – P(A∩B)]
= 1 – [0.25 + 0.50 – 0.14]
= 1 – 0.61 = 0.39
Q11.
Answer :
(c) 1/3
Total number of sample space, S = {1, 2, 3, 4, 5, 6}
∴ n(S) = 6
Let A be the event of getting the number 1 or 6.
A = {1, 6}
i.e. n(A) = 2
Hence, required probability = nAnS=26=13
Page No.33.70 (Multiple Choice Questions)
Q12.
Answer :
(d) 1132
Total number of ways in which six boys and six girls can be seated in a row = (12)!
Taking all the six girls as one person, seven persons can be seated in a row in 7! ways. The six girls can be arranged among themselves in 6! ways.
Then number of ways in which six boys and six girls can be seated in a row so that all the girls sit together = 7! × 6!
∴ Required probability = 7!×6!12!=72012×11×10×9×8=1132
Q13.
Answer :
(b) is false
Since the events A, B and C are mutually exclusive, we have:
PA∪B∪C=23+14+16=1312>1 , which is not possible.
Hence, the given statement is false.
Q14.
Answer :
(b) (−1/4, 1/3)
P(A) = (1 − 3p)/2
P(B) = (1 + 4p)/3
P(C) = (1 + p)/6
The events are mutually exclusive and exhaustive.
∴ P(A ∪ B ∪ C) = P(A) + P(B) + P(C) = 1
⇒ 0≤PA≤1, 0≤PB≤1, 0≤PC≤1
⇒ 0≤1-3p2≤1, 0≤1+4p3≤1, 0≤1+p6≤1
⇒-1/3≤p≤13, …(i)
-14≤p≤12 …(ii)
and -1≤p≤5 …(iii)
The common solution of (i), (ii) and (iii) is -1/4≤p≤1/3.
∴ The set values of p are (-1/4 , 1/3)
Q15.
Answer :
(c) 920
We have:
P(both are aces) = 4C2 16C2= 416×315=120
P(one is ace) = 4C1×12C1C162=25
∴ P(at least one is ace) = 120+25=920
Q16.
Answer :
(c) 1/36
When three dice are thrown together, the sample space S associated with the random experiment is given by
S = {(1, 1, 1), (1, 1, 2), (1, 1, 3) …(6, 6, 5), (6, 6, 6)}
Clearly, total number of elementary events n(S) = 216
Let A be the event of getting a total score of 5.
Then A = { (1, 1, 3), (1, 3, 1), (3, 1, 1), (1, 2, 2), (2, 1, 2), (2, 2, 1)}
∴ Favourable number of elementary events = 6
i.e. n(A) = 6
Hence, required probability = 6216=136
Q17.
Answer :
(d) 3 : 2
Let P(B) = x
Then, P(A) = 2×3
P(A) + P(B) = x+2×3=5×3
⇒5×3=1 (∵ They are exhaustive events)
⇒x=35
Now, P(A)=25 and PB=35
∴ Odd in favour of B = 3/51-3/5=32=3:2
Q18.
Answer :
(b) 3/7
We know that a leap year has 366 days (i.e. 7 × 52 + 2) = 52 weeks and 2 extra days
The sample space for these 2 extra days is given below:
S = {(Sunday, Monday), (Monday, Tuesday), (Tuesday, Wednesday), (Wednesday, Thursday), (Thursday, Friday), (Friday, Saturday), (Saturday, Sunday)}
There are 7 cases.
∴ n(S) = 7
Let E be the event that the leap year has 53 Fridays or 53 Saturdays.
E = { (Thursday, Friday), (Friday, Saturday), (Saturday, Sunday)}
i.e. n(E) = 3
∴PE=nEnS=37∴P(E)=n(E)n(S)=37
Hence, the probability that a leap year has 53 Fridays or 53 Saturdays is 37.
Q19.
Answer :
(d) 2324
Total number of ways of placing four letters in 4 envelops = 4! = 24
All the letters can be dispatched in the right envelops in only one way. Therefore, the probability that all the letters are placed in the right envelops is 124.
Hence, probability that all the letters are not placed in the right envelops = 1-124=2324
Q20.
Answer :
(a) 0.39
P (A) = 0.25 and P (B) = 0.50
P(A∩B) = 0.14
∴ Required probability = 1 – P(A∪B)
= 1 – [P(A) + P(B) – P(A∩B)]
= 1 – [0.25 + 0.50 – 0.14]
= 1 – 0.61 = 0.39
Q21.
Answer :
(c) 19/50
Given:
P(A) = 15
∴ P(A’) = 1-15=45
P(B) = 310
∴ P(B’) = 1-310=730
Hence, required probability = P(A∩ B’) + P(A’∩ B)
= 15×710+45×310= 750+1250=1950
Q22.
Answer :
(a) 6464
The answer is one, because the article would be either good or defective as per the question.
Hence, the only option is 6464=1.
Q23.
Answer :
(c) 17/19
Number of ways in which we can choose three distinct integers from 20 integers = 20C3 = 1140
We know that, if we take three odd numbers, there product will always be an odd number.
Out of 20 consecutive integers, 10 are even and 10 are odd integers.
Number of ways in which we can choose three distinct odd integers from 10 odd integers= 10C3 = 120
P(product is even) = 1 – P(product is odd)
= 1-1201140=1140-1201140=10201140=1719
Q24.
Answer :
(c) 15/29
The total number of ways in which two integers can be chosen from the given 30 integers is 30C2.
The sum of the selected numbers is odd if exactly one of them is even or odd.
∴ Favourable number of outcomes = 15C1 × 15C1
Hence, required probability = C115×C115C230=1529
Q25.
Answer :
(d) 2/3
Out of 12 balls, one ball can be drawn in 12C1 ways.
∴ Total number of elementary events = 12C1 = 12
Out of fivne black balls, one black ball can be chosen in 5C1 = 5 ways.
Out of three red balls, one red ball can be chosen in 3C1 = 3 ways.
∴ Favourable number of events = 5 + 3 = 8
Hence, required probability = 812=23
Q26.
Answer :
(a) 1/36
When two dice are thrown simultaneously, the sample space associated with the random experiment is given by:
S = {(1, 1), (1, 2), (1, 3) …(6, 4), (6, 5), (6, 6)}
Clearly, total number of elementary events = 36
Let A be the event of getting a pair of aces.
Then A = {(1, 1)}
∴ n(A) = 1
Hence, required probability = nAnS=136
Q27.
Answer :
(a) 5/84
Three balls can be drawn randomly from nine balls in 9C3 = 84 ways.
Three balls cannot be red as there are only two red balls.
Three balls of the same colour can be drawn in the following ways :
3 blue out of a total of 3 blue balls.
The probability for which is C3384=184.
3 black out of a total of 4 black balls.
The probability for which is C3484=484.
Hence, required probability = 184+484=584
Page No.33.71 (Multiple Choice Questions)
Q28.
Answer :
(a) P5775
Since, it is an eight-storey building.
So, there are 7 possible options for them in 7 floors in total if ground floor is not considered.
Hence, total possible outcomes = 7× 7× 7 × 7 × 7= 75
Thus, number of ways in which 5 persons can leave from seven floors differently = 7P5
∴ Required probability = P5775
Q29.
Answer :
(a) 6464
Let A be the event of drawing one good article whereas B be the event of drawing one defected article.
Here,
PA=1010+6=1016 and PB=610+6=616
The events A and B are mutually exclusive. Thus, the required probability is PA∪B=PA+PB.
⇒PA∪B=1016+616=1616=1
Hence, the correct option is (a).
Q30.
Answer :
(c) 11/16
If the numbers of nails and nuts are 6 and 10, respectively, then the numbers of rusted nails and rusted nuts are 3 and 5, respectively.
Total number of items = 6 + 10 = 16
Total number of rusted items = 3 + 5 = 8
Total number of ways of drawing one item = 16C1
Let R and N be the events where both the items drawn are rusted items and nails, respectively.
R and N are not mutually exclusive events, because there are 3 rusted nails.
P(either a rusted item or a nail ) = P (R ∪ N)
= P(R) + P (N) – P (R ∩ N)
= C16C116+C18C116-C13C116
= 616+816-316=1116
Q31.
Answer :
(a) 1/4
Let P(B) = p
Then P(A) = 13p
Since A and B are two mutually exclusive events, we have:
A ∪ B = S
⇒ P (A∪B) = P (S)
⇒ P (A∪B) = 1
⇒ P (A) + P (B) = 1
⇒ 13p+p=1
⇒ 4p3=1⇒p=34
∴ P (A) = 13p=13×34=14
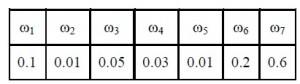
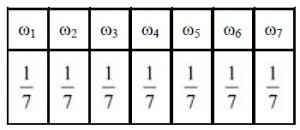
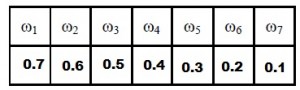
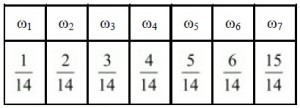
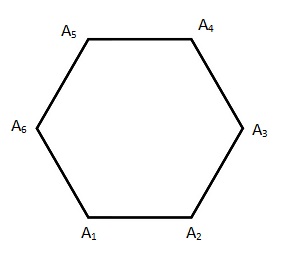

Leave a Reply