Page 23.13 Ex 23.1
Q1.
Answer :
(i) θ=-π4
∴ Slope of the line=m=tanθ⇒Slope of the line=tan-π4=-tanπ4=-1
Hence, the slope of the line is -1.
(ii) θ=2π3
∴ Slope of the line=m=tanθ⇒Slope of the line=tan2π3=-tanπ3=-3
Hence, the slope of the line is -3.
(iii) θ=3π4
∴ Slope of the line=m=tanθ⇒Slope of the line=tan3π4=-tanπ4=-1
Hence, the slope of the line is -1.
(iv) θ=π3
∴ Slope of the line=m=tanθ⇒Slope of the line=tanπ3=3
Q2.
Answer :
(i) (−3, 2) and (1, 4)
Let m be the slope of the given line.
∴ m=y2-y1x2-x1⇒m=4-21+3=24=12
Hence, the slope of the line passing through the points (−3, 2) and (1, 4) is 12.
(ii) (at12, 2at1) and (at22, 2at2)
Let m be the slope of the given line.
∴ m=y2-y1x2-x1⇒m=2at2-2at1at22-at12=2t2-t1t2-t1t2+t1=2t1+t2
Hence, the slope of the line passing through the points (at12, 2at1) and (at22, 2at2) is 2t1+t2.
(iii) (3, −5), and (1, 2)
Let m be the slope of the given line.
∴ m=y2-y1x2-x1⇒m=2+51-3=-72
Hence, the slope of the line passing through the points (3, −5), and (1, 2) is -72.
Q3.
Answer :
(i) Through (5, 6) and (2, 3); through (9, −2) and (6, −5)
Let m1 be the slope of the line joining (5, 6) and (2, 3) and m2 be the slope of the line joining (9, −2) and (6, −5).
∴ m1=y2-y1x2-x1=3-62-5=-3-3=1 and m2=y2-y1x2-x1=-5+26-9=-3-3=1
Since, m1=m2
Therefore, the given lines are parallel.
(ii) Through (9, 5) and (−1, 1); through (3, −5) and (8, −3)
Let m1 be the slope of the line joining (9, 5) and (−1, 1) and m2 be the slope of the line joining (3, −5) and (8, −3).
∴ m1=y2-y1x2-x1=1-5-1-9=-4-10=25 and m2=y2-y1x2-x1=-3+58-3=25
Since, m1=m2
Therefore, the given lines are parallel.
(iii) Through (6, 3) and (1, 1); through (−2, 5) and (2, −5).
Let m1 be the slope of the line joining (6, 3) and (1, 1) and m2 be the slope of the line joining (−2, 5) and (2, −5).
∴ m1=y2-y1x2-x1=1-31-6=-2-5=25 and m2=y2-y1x2-x1=-5-52+2=-104=-52
Now, m1m2=25×-52=-1Since, m1m2=-1
Therefore, the given lines are perpendicular.
(iv) Through (3, 15) and (16, 6); through (−5, 3) and (8, 2).
Let m1 be the slope of the line joining (3, 15) and (16, 6) and m2 be the slope of the line joining (−5, 3) and (8, 2).
∴ m1=y2-y1x2-x1=6-1516-3=-913 and m2=y2-y1x2-x1=2-38+5=-113
Now, m1m2=-913×-113=9169Since, m1m2≠-1 and m1≠m2
Therefore, the given lines are neither parallel nor perpendicular.
Q4.
Answer :
(i) We know that the angle between the coordinate axes is π2.
The line bisects the first quadrant angle.
Inclination of the line with the positive x-axis = 12π2=π4
∴ Slope of the line=tanπ4=1
(ii) The line makes an angle of 30∘ with the positive direction of the y-axis measured anticlockwise
Since the line makes an angle of 30° with the positive direction of the y-axis measured anticlockwise,
it makes an angle of 90°+30°=120° with the positive direction of the x-axis measured anticlockwise.
∴ Slope of the line=tan120°=-tan60°=-3
Q5.
Answer :
(i) A (4, 8), B (5, 12), C (9, 28)
Slope of AB = y2-y1x2-x1=12-85-4=41=4
Slope of BC = y2-y1x2-x1=28-129-5=164=4
Since, Slope of AB = Slope of BC = 4
Therefore, the given points are collinear.
(ii) A (16, − 18), B (3, −6), C (−10, 6)
Slope of AB = y2-y1x2-x1=-6+183-16=-1213
Slope of BC = y2-y1x2-x1=6+6-10-3=-1213
Since, Slope of AB = Slope of BC = -1213
Therefore, the given points are collinear.
Q6.
Answer :
Let m1 be the slope of the line passing through (3, y) and (2, 7) and m2 be the slope of the line passing through (−1, 4) and (0, 6).
∴ m1=y2-y1x2-x1=7-y2-3=7-y-1=y-7 and m2=y2-y1x2-x1=6-40+1=21=2
For both the lines to be parallel, we must have,
m1=m2⇒y-7=2 ⇒ y=9
Hence, the value of y is 9.
Q7.
Answer :
(i) zero
If the slope of a line is zero, then the line is either the x-axis itself or it is parallel to the x-axis.
(ii) positive
We know that the value of tanθ is positive for the value of θ in the first quadrant. Therefore, the line makes an acute angle with the positive direction of the x-axis.
(iii) negative
We know that the value of tanθ is negative for the value of θ in the second quadrant. Therefore, the line makes an obtuse angle with the positive direction of the x-axis.
Q8.
Answer :
Let m1 be the slope of the line joining the points (2, −3) and (−5, 1) and m2 be the slope of the line joining the points (7, −1) and (0, 3).
∴ m1=y2-y1x2-x1=1+3-5-2=-47 and m2=y2-y1x2-x1=3+10-7=-47
Since, m1 = m2
Hence, the line joining (2, −3) and (−5, 1) is parallel to the line joining (7, −1) and (0, 3).
Q9
Answer :
Let m1 be the slope of the line joining the points (2, −5) and (−2, 5) and m2 be the slope of the line joining the points (6, 3) and (1, 1).
∴ m1=y2-y1x2-x1=5+5-2-2=10-4=-52 and m2=y2-y1x2-x1=1-31-6=-2-5=25
Now, m1m2=-52×25=-1Since, m1m2=-1
Hence, the line joining (2, −5) and (−2, 5) is perpendicular to the line joining (6, 3) and (1, 1).
Q10.
Answer :
We have, A (0, 4), B (1, 2) and C (3, 3)
Now,
m1=Slope of AB=2-41-0=-2
m2=Slope of BC=3-23-1=12
m3=Slope of CA=4-30-3=-13
∴m1m2=-2×12=-1
Therefore, AB is perpendicular to BC, i.e. ∠ABC=90∘.
Thus, the given points are the vertices of a right angled triangle.
Q11.
Answer :
Let A (−4, −1), B (−2, −4), C (4, 0) and D (2, 3) be the given points.
Let us find the lengths of AB, BC, CD and DA
AB=-2+42+-4+12=13BC=4+22+0+42=213CD=2-42+3-02=13DA=2+42+3+12=213
∴ AB = CD and BC = DA
Now, we have,
m1=Slope of AB=-4+1-2+4=-32m2=Slope of BC=0+44+2=46=23m3=Slope of CD=3-02-4=-32
Here, m1m2=-3223=-1 and m1=m3
Therefore, we have,
AB = CD
BC = DA
AB⊥BC
And, AB is parallel to DC.
Hence, the given points are the vertices of a rectangle.
Q12.
Answer :
The given points are A (h, 0), P (a, b) and B (0, k).
Thus, we have,
Slope of AP=b-0a-hSlope of BP=b-ka-0
For the given points to be collinear, we must have,
Slope of AP = Slope of BP
⇒b-0a-h=b-ka-0⇒ba-h=b-ka⇒ab=ab-ak-bh+hk⇒ak+bh=hk⇒ah+bk=1 On dividing both sides by hk
Q13.
Answer :
Let m1 and m2 be the slopes of the given lines.
∴ m2=2m1
Let θ be the angle between the given lines.
∴ tanθ=m2-m11+m1m2⇒13=2m1-m11+2m12=m11+2m12⇒m11+2m12=±13
Taking the positive sign, we get,
3m1=1+2m12⇒2m12-3m1+1=0⇒2m1-1m1-1=0⇒m1=12, 1
Taking the negative sign, we get,
-3m1=1+2m12⇒2m12+3m1+1=0⇒2m1+1m1+1=0⇒m1=-12, -1
Hence, the slopes of the other line are ±12, ±1.
Q14.
The graph shown is a line.
∴ Slope of AB=97-921995-1985=510=12
The points A, B and C lie on the same line.
∴ Slope of BC=Slope of AB⇒P-972010-1995=12⇒P-97=2010-19952⇒P=97+7.5⇒P=104.5
Hence, the population in the year 2010 was 104.50 crores.
Page 23.14 Ex 23.1
Q15.
Answer :
Let A (−2, −1), B (4, 0), C (3, 3) and D (−3, 2) be the given points.
Now, slope of AB=0+14+2=16
Slope of BC=3-03-4=-3
Slope of CD=2-3-3-3=16
Slope of DA=-1-2-2+3=-3
Clearly, we have,
Slope of AB = Slope of CD
Slope of BC = Slope of DA
As the slopes of opposite sides are equal,
Therefore, both pair of opposite sides are parallel.
Hence, the given points are the vertices of a parallelogram.
Q16.
Answer :
Let the given points be A (3, −1) and B (4, −2).
∴ Slope of AB = -2+14-3=-1
Let θ be the angle between the x-axis and AB.
∴ tanθ=-1⇒θ=tan-1-1=135∘
Hence, the angle between the x-axis and the line joining the points (3, −1) and (4, −2) is 135∘.
Q17.
Answer :
Let the given points be A (−2, 6), B (4, 8), P (8, 12) and Q (x, 24).
Slope of AB = m1 = 8-64+2=26=13
Slope of PQ = m2 = 24-12x-8=12x-8
It is given that the line joining A (−2, 6) and B (4, 8) and the line joining P (8, 12) and Q (x, 24) are perpendicular.
∴ m1m2=-1⇒13×12x-8=-1⇒x-8=-4⇒x=4
Hence, the value of x is 4.
Q18.
Answer :
Let the given points be A (x, −1), B (2, 1) and C (4, 5).
Slope of AB = 1+12-x=22-x
Slope of BC = 5-14-2=42=2
It is given that the points (x, −1), (2, 1) and (4, 5) are collinear.
∴ Slope of AB = Slope of BC
⇒22-x=2⇒1=2-x⇒x=1
Hence, the value of x is 1.
Q19.
Answer :
Let the given points be A (3, −1) and B (4, −2).
∴ Slope of AB = -2+14-3=-1
Let θ be the angle between the x-axis and AB.
∴ tanθ=-1⇒θ=tan-1-1=3π4
Hence, the angle between the x-axis and the line joining the points (3, −1) and (4, −2) is 3π4.
Q20.
Answer :
Let A (−2, −1), B (4, 0), C (3, 3) and D (−3, 2) be the given points.
Now, slope of AB=0+14+2=16
Slope of BC=3-03-4=-3
Slope of CD=2-3-3-3=16
Slope of DA=-1-2-2+3=-3
Clearly, we have,
Slope of AB = Slope of CD
Slope of BC = Slope of DA
As the slopes of opposite sides are equal,
Therefore, both pair of opposite sides are parallel.
Hence, the given points are the vertices of a parallelogram.
Q21.
Answer :
Let A (4, 1), B (1, 7), C (−6, 0) and D (−1, −9) be the vertices of the given quadrilateral.
Let P, Q, R and S be the mid-points of AB, BC, CD and DA, respectively.
So, the coordinates of P, Q, R and S are P 52, 4, Q -52,72, R -72,-92 and S 32, -4.
In order to prove that PQRS is a parallelogram, it is sufficient to show that PQ is parallel to RS and PQ is equal to RS.
Now, we have,
Slope of PQ=72-4-52-52=110
Slope of RS=-4+9232+72=110
Clearly, Slope of PQ = Slope of RS
Therefore, PQ ∥ RS
PQ=-52-522+72-42=1012
RS=32+722+-4+922=1012
Therefore, PQ = RS
Thus, PQ ∥ RS and PQ = RS
Hence, the mid-points of the sides of the given quadrilateral form a parallelogram.
Page 23.17 Ex 23.2
Q1.
Answer :
The equation of a line parallel to the x-axis is y = k
It is given that y = k passes through (3, −5)
∴ −5 = k
⇒ k = −5
Hence, the equation of the required line is y = −5
Q2.
Answer :
The equation of the line perpendicular to the x-axis is x = k.
It is given that x = k has intercept −2 on the x-axis. This means that the line x = k passes through (−2, 0).
∴ −2 = k
⇒ k = −2
Hence, the equation of the line that is perpendicular to the x-axis and has intercept − 2 on the x-axis is x = −2.
Q3.
Answer :
The equation of a line parallel to the x-axis is y = k.
It is given that y = k has intercept −2 on the y-axis. This means that the line y = k passes through (0, −2).
∴ −2 = k
⇒ k = −2
Hence, the equation of the required line is y = −2.
Q4.
Answer :
The lines x = − 3 and x = 2 are parallel to the y-axis. They pass through (−3, 0) and (2, 0), respectively.
Similarly, the lines y = − 2, y = 3 are parallel to the x-axis. They pass through (0, −2) and (0, 3), respectively.
The lines x = − 3, x = 2, y = − 2 and y = 3 are drawn as shown in the following figure.
Clearly, the coordinates of the square that is formed are (2, 3), (−3, 3), (−3, −2) and (2, −2).
Q5.
Answer :
The equation of the line parallel to the x-axis is y = b.
It is given that y = b passes through (4, 3).
∴ 3 = b
⇒ b = 3
Thus, the equation of the line parallel to the x-axis and passing through (4, 3) is y = 3.
Similarly, the equation of the line perpendicular to the x-axis is x = a.
It is given that x = a passes through (4, 3).
∴ 4 = a
⇒ a = 4
Thus, the equation of the line perpendicular to the x-axis and passing through (4, 3) is x = 4.
Hence, the required lines are x = 4 and y = 3.
Q6.
Answer :
The lines x = − 2 and x = 6 pass through the points (−2, 0) and (6, 0), respectively.
Let (h, k) be the mid-point of the line joining the points (−2, 0) and (6, 0).
∴ h, k=-2+62, 0=2, 0
The given lines are parallel to the y-axis and the required line is equidistant from theses lines.
Hence, the required line is parallel to the y-axis, which is given by x = k.
This line passes through (2, 0).
∴ 2 = k
⇒ k = 2
Hence, the equation of a line that is equidistant from the lines x = − 2 and x = 6 is x = 2.
Q7.
Answer :
The lines y = 10 and y = −2 pass through the points (0, 10) and (0, −2), respectively.
Let (h, k) be the mid-point of the line joining the points (0, 10) and (0, −2).
∴ h, k=0,10-22=0, 4
The given lines are parallel to the x-axis and the required line is equidistant from these lines.
Hence, the required line is parallel to the x-axis, which is given by y = k.
This line passes through (0, 4).
∴ 4 = k
⇒ k = 4
Hence, the equation of a line that is equidistant from the lines y = 10 and y = − 2 is y = 4.
Page 23.19 Ex 23.3
Q1.
Answer :
Here, m=tan150∘=-tan30∘=-13
and c = y-intercept = 2
Substituting the values of m and c in y = mx + c, we get,
y=-13x+2⇒x+3y=23
Hence, the equation of the required line is x+3y=23.
Q2.
Answer :
(i) Here, m = 2, c = 3
Substituting the values of m and c in y = mx + c, we get,
y = 2x + 3
Hence, the equation of the straight line with slope 2 and y-intercept 3 is y = 2x + 3
(ii) Here, m=-13, c=-4
Substituting the values of m and c in y = mx + c, we get,
y=-x3-4⇒x+3y+12=0
Hence, the equation of the straight line with slope -13 and y-intercept 4 is x + 3y + 12 = 0
(iii) Here, m = −2
Substituting the value of m in y = mx + c, we get,
y = −2x + c
It is given that the line y = −2x + c intersects the x-axis at a distance of 3 units to the left of the origin.
This means that the required line passes trough the point (−3, 0).
∴ 0=-2×-3+c⇒c=-6
Hence, the equation of the required line is y = −2x − 6, i.e. 2x + y + 6 = 0
Q3.
Answer :
There are two bisectors of the coordinate axes.
Their inclinations with the positive x-axis are 45∘ and 135∘.
So, the slope of the bisector is m=tan45∘ or m=tan135∘, i.e. m=1 or m=-1 and c = 0.
Substituting the values of m and c in y = mx + c, we get,
y = x + 0
⇒ x – y = 0
or y = – x + 0
⇒ x + y = 0
Hence, the equation of the bisector is x±y=0.
Q4.
Answer :
Let m be the slope of the required line.
∴ m=tanθ=tantan-13=3 c=y-intercept=-4
Substituting the values of m and c in y = mx + c, we get y = 3x – 4
Hence, the equation of the required line is y = 3x – 4
Page 23.20 Ex 23.3
Q5.
Answer :
Let m be the slope of the required line.
c = y-intercept = -4
It is given that the required line is parallel to the line joining the points (2, −5) and (1, 2).
∴ m=y2-y1x2-x1=2+51-2=-7
Substituting the values of m and c in y = mx + c, we get,
y = -7x – 4
⇒ 7x + y + 4 = 0
Hence, the equation of the required line is 7x + y + 4 = 0
Q6.
Answer :
Let m be the slope of the required line.
Here, c = y-intercept = 3
Slope of the line joining the points (4, 2) and (3, 5) = 5-23-4=-3
It is given that the required line is perpendicular to the line joining the points (4, 2) and (3, 5).
∴m×Slope of the line joining the points 4, 2 and 3, 5=-1⇒m×-3=-1⇒m=13.
Substituting the values of m and c in y = mx + c, we get,
y=13x+3 ⇒ x-3y+9=0
Hence, the equation of the required line is x -3y + 9 = 0
Q7.
Answer :
Let m be the slope of the required line.
Here, c = y-intercept = -3
Slope of the line joining the points (4, 3) and (−1, 1) = 1-3-1-4=25
It is given that the required line is perpendicular to the line joining the points (4, 3) and (−1, 1).
∴ m×Slope of the line joining the points 4, 3 and -1, 1=-1⇒m×25=-1⇒m=-52
Substituting the values of m and c in y = mx + c, we get:
y=-52x-3 ⇒5 x+2y+6=0
Hence, the equation of the required line is 5x + 2y + 6 = 0.
Q8.
Answer :
Let m be the slope of the required line.
∴m=tanθ=tan30∘=13Here, c=y-intercept=2
Substituting the values of m and c in y = mx + c, we get:
y=13x+2 ⇒ x-3y+23=0
Hence, the equation of the required line is x-3y+23=0.
Page 23.28 Ex 23.4
Q1.
Answer :
Here, m=-3, x1=6 and y1=2
Substituting these values in y-y1=mx-x1, we get,
y-2=-3x-6⇒y-2=-3x+18⇒3x+y-20=0
Hence, the equation of the required line is 3x+y-20=0
Q2.
Answer :
Here, m=tan45∘=1×1=-2 and y1=3
Substituting these values in y-y1=mx-x1, we get:
y-3=1x+2⇒y-3=x+2⇒x-y+5=0
Hence, the equation of the required line is x-y+5=0
Q3.
Answer :
Let the required line divide the line joining the points A 2, 3 and B -5, 8 at P (x1, y1).
Here, AP : PB = 3 : 4
∴ P x1, y1=4×2-5×33+4, 4×3+3×83+4=-1, 367
Now, slope of AB = 8-3-5-2=-57
Let m be the slope of the required line.
Since, the required line is perpendicular to the line joining the points A 2, 3 and B -5, 8
∴ m×Slope of the line joining the points A2, 3 and B-5, 8=-1⇒m×-57=-1⇒m=75
Substituting m=75, x1=-1 and y1=367 in y-y1=mx-x1 we get,
y-367=75x+1⇒35y-180=49x+49⇒49x-35y+229=0
Hence, the equation of the required line is 49x-35y+229=0
Q4.
Answer :
Let PD be the perpendicular drawn from P (4, 1) on the line joining the points A2, -1 and B6, 5.
Let m be the slope of PD.
∴ m × Slope of AB=-1⇒m × 5+16-2=-1⇒m × 64=-1⇒m × 32=-1⇒m=-23
Thus, the equation of line PD passing through P (4, 1) and having slope -23 is
y-1=-23x-4⇒3y-3=-2x+8⇒2x+3y-11=0
Let D divide the line AB in the ratio k : 1
Then, the coordinates of D are 6k+2k+1, 5k-1k+1.
Since, D lies on AB whose equation is 2x+3y-11=0
Therefore, it satisfy the equation.
∴ 26k+2k+1+35k-1k+1-11=0⇒12k+4+15k-3-11k-11=0⇒16k=10⇒k=58
Hence, the perpendicular drawn from the point (4, 1) on the line joining the points (2, −1) and (6, 5) divides it in the ratio 5 : 8
Q5.
Answer :
Let mAD, mBE and mCF be the slopes of the altitudes AD, BE and CF, respectively.
∴ Slope of AD × Slope of BC=-1⇒mAD ×0-1-1-1=-1⇒mAD ×12=-1⇒mAD = -2
Slope of BE × Slope of AC=-1⇒mBE×0+2-1-2=-1⇒mBE×-23=-1⇒mBE=32
Slope of CF × Slope of AB=-1⇒mCF×1+21-2=-1⇒mCF×-3=-1⇒mCF=13
Now, the equation of AD which passes through A (2, −2) and has slope −2 is
y+2=-2x-2⇒2x+y-2=0
The equation of BE, which passes through B (1, 1) and has slope 32 is
y-1=32x-1⇒3x-2y-1=0
The equation of CF, which passes through C (−1, 0) and has slope 13 is
y-0=13x+1⇒x-3y+1=0
Q6.
Answer :
Let the given points be A (3, 4) and B (−1, 2).
Let M be the midpoint of AB.
∴ Coordinates of M=3-12, 4+22=1, 3
And, slope of AB = 2-4-1-3=12
Let m be the slope of the right bisector of the line joining the points (3, 4) and (−1, 2).
∴ m×Slope of AB=-1⇒m×12=-1⇒m=-2
So, the equation of the line that passes through M (1, 3) and has slope −2 is
y-3=-2x-1 ⇒2x+y-5=0
Hence, the equation of the right bisector of the line segment joining the points (3, 4) and (−1, 2) is 2x+y-5=0.
Q7.
Answer :
The graph of the required line is shown below.
The line which is inclined at an angle of 60° with the positive direction of y-axis makes an angle of 30° with x-axis.
Clearly, the slope of the required line is m=tan30∘=13
So, the equation of the required line having slope 13 and passes through the point P3, -2 is
y+2=13x-3⇒x-3y-3-23=0
Hence, the equation of the required line is x-3y-3-23=0
Q8.
Answer :
Let θ be the inclination of the line with the positive x-axis.
Then, we have,
sinθ=35⇒tanθ=sinθ1-sin2θ=351-3252352-32=34
So, the equation of the line that passes through (1, 2) and has slope 34 is
y-2=34x-1⇒3x-4y+5=0
Hence, the equation of the required line is 3x-4y+5=0
Q9.
Answer :
The given points are A 2, 5 and B -3, 6.
∴ Slope of AB =6-5-3-2=-15
Let m be the slope of the required line. Then,
m×Slope of AB=-1⇒m×-15=-1⇒m=5
So, the equation of the line that passes through (−3, 5) and has slope 5 is
y-5=5x+3⇒5x-y+20=0
Hence, the equation of the required line is 5x-y+20=0
Q10.
Answer :
The given points are A (1, 0) and B (2, 3).
Let M be the midpoint of AB.
∴ Coordinates of M=1+22, 0+32=32, 32
And, slope of AB = 3-02-1=3
Let m be the slope of the perpendicular bisector of the line joining the points A (1, 0) and B (2, 3).
∴ m×Slope of AB=-1⇒m×3=-1⇒m=-13
So, the equation of the line that passes through M 32, 32 and has slope -13 is
y-32=-13x-32⇒x+3y-6=0
Hence, the equation of the right bisector of the line segment joining the points A (1, 0) and B (2, 3) is x+3y-6=0.
Q11.
Answer :
The inclinations of the two lines with the positive x-axis are π3 and 2π3.
So, their slopes are m1=tanπ3=3 and m2=tan2π3=-tanπ3=-3.
Now, the equations of the lines that pass through (0, 2) and have slopes m1 and m2 are
y-2=3x-0 and y-2=-3x-0⇒y-3x-2=0 and y+3x-2=0or 3x-y+2=0 and 3x+y-2=0
Now, the equation of the line parallel to the line having slope m1 and intercept c = -2 is
y=m1x+c⇒y=3x-2⇒3x-y-2=0
Similarly, the equation of line parallel to the line having slope m2 and intercept c = -2 is
y=m2x+c⇒y=-3x-2⇒3x+y+2=0
Q12.
Answer :
It is given that the lines are equally inclined to the axes.
So, their inclinations with the positive x-axis are 45∘ and 135∘.
Let m1 and m2 be the slopes of the lines.
∴ m1=tan45∘=1 and m2=tan135∘=-tan45∘=-1
Thus, the equations of the lines passing through (0, 5) with slopes 1 and -1 are
y-5=1x-0 and y-5=-1x-0⇒y-x-5= and y+x-5=0⇒y=x+5 and x+y=5
Q13.
Answer :
The required line is shown in the following figure.
The line which is inclined at an angle of 135° with the positive direction of y-axis makes an angle of 45° with x-axis.
Here, m=tan45∘=1
Thus, the equation of the required line passing through (2, 0) with slope 1 is
y-0=1x-2 ⇒x-y-2=0
Q14.
Answer :
The equation of the line passing through (x1, y1) with slope m is given by
y-y1=mx-x1
So, the equation of the line passing through (0, 0) with slope m is
y-0=mx-0 ⇒y=mx
Q15.
Answer :
Here, m=tan75∘⇒m=tan45∘+30∘⇒m=tan45∘+tan30∘1-tan45∘tan30∘⇒m=1+131-13=3+13-1⇒m=3+13-1×3+13+1=2+3
So, the equation of the line that passes through (2, 23) and has slope 2+3 is
y-23=2+3x-2⇒y-23=2+3x-4-23⇒2+3x-y-4=0
Page 23.34 Ex 23.5
Q1.
Answer :
(i) (0, 0) and (2, −2)
Here, x1, y1≡0, 0 x2, y2≡2, -2
So, the equation of the line passing through the two points (0, 0) and (2, −2) is
y-y1=y2-y1x2-x1x-x1⇒y-0=-2-02-0x-0⇒y=-x
(ii) (a, b) and (a + csin α, b + ccos α)
Here, x1, y1≡a, b x2, y2≡a+csinα, b+ccosα
So, the equation of the line passing through the two given points is
y-y1=y2-y1x2-x1x-x1⇒y-b=b+ccosα-ba+csinα-ax-a⇒y-b=cotαx-a
(iii) (0, −a) and (b, 0)
Here, x1, y1≡0, -a x2, y2≡b, 0
So, the equation of the line passing through the two points is
y-y1=y2-y1x2-x1x-x1⇒y+a=0+ab-0x-0⇒ax-by=ab
(iv) (a, b) and (a + b, a − b)
Here, x1, y1≡a, b x2, y2≡a+b, a-b
So, the equation of the line passing through the two points is
y-y1=y2-y1x2-x1x-x1⇒y-b=a-b-ba+b-ax-a⇒by-b2=a-2bx-a2+2ab⇒a-2bx-by+b2+2ab-a2=0
(v) (at1, a/t1) and (at2, a/t2)
Here, x1, y1≡at1, at1 x2, y2≡at2, at2
So, the equation of the line passing through the two points is
y-y1=y2-y1x2-x1x-x1⇒y-at1=at2-at1at2-at1x-at1⇒y-at1=-1t2t1x-at1⇒x+t1t2y=at1+t2
(vi) (acos α, asin α) and (acos β, asin β)
Here, x1, y1≡acosα, asinα x2, y2≡acosβ, asinβ
So, the equation of the line passing through the two points is
y-y1=y2-y1x2-x1x-x1⇒y-asinα=asinβ-asinαacosβ-acosαx-acosα⇒y-asinα=sinβ-sinαcosβ-cosαx-acosα
⇒ycosβ-cosα-xsinβ-sinα-asinαcosβ+asinαcosα+acosαsinβ-acosαsinα=0⇒ycosβ-cosα-xsinβ-sinα=asinαcosβ-acosαsinβ⇒2ysinα+β2sinα-β2-2xsinβ-α2cosα+β2=asinα-β⇒2ysinα+β2sinα-β2+2xsinα-β2cosα+β2=2asinα-β2cosα-β2⇒xcosα+β2+ysinα+β2=acosα-β2 dividing by sinα-β2
Q2.
Answer :
(i) Let the given points be A (1, 4), B (2, −3) and C (−1, −2).
Let m1, m2 and m3 be the slopes of the sides AB, BC and CA, respectively.
∴ m1=-3-42-1, m2=-2+3-1-2 and m3=4+21+1⇒m1=-7, m2=-13 and m3=3
So, the equations of the sides AB, BC and CA are
y-4=-7x-1, y+3=-13x-2 and y+2=3x+1⇒7x+y=11, x+3y+7=0 and 3x-y+1=0
(ii) Let the given points be A (0, 1), B (2, 0) and C (−1, −2).
Let m1, m2 and m3 be the slopes of the sides AB, BC and CA, respectively.
∴ m1=0-12-0, m2=-2-0-1-2 and m3=1+20+1⇒m1=-12, m2=23 and m3=3
So, the equations of the sides AB, BC and CA are
y-1=-12x-0, y-0=23x-2 and y+2=3x+1⇒x+2y=2, 2x-3y=4 and 3x-y+1=0
Q3.
Answer :
Let A (−1, 6), B (−3, −9) and C (5, −8) be the coordinates of the given triangle.
Let D, E and F be midpoints of BC, CA and AB, respectively.
So, the coordinates of D, E and F are
D≡-3+52, -9-82=1, -172E≡-1+52, 6-82=2, -1F≡-1-32, 6-92=-2, -32
Median AD passes through A -1, 6 and D 1, -172.
So, its equation is
y-6=-172-61+1x+1⇒4y-24=-29x-29⇒29x+4y+5=0
Median BE passes through B -3, -9 and E 2, -1.
So, its equation is
y+9=-1+92+3x+3⇒5y+45=8x+24⇒8x-5y-21=0
Median CF passes through C 5, -8 and F -2, -32.
So, its equation is
y+8=-32+8-2-5x-5⇒-14y-112=13x-65⇒13x+14y+47=0
Q4.
Answer :
The rectangles formed by the lines x = a, x = a’, y = b and y = b’ is shown below:
Clearly, the vertices of the rectangle are A a, b, B a’, b, C a’, b’ and D a, b’.
The diagonal passing through A a, b and C a’, b’ is
y-b=b’-ba’-ax-a⇒a’-ay-ba’-a=b’-bx-ab’-b⇒a’-ay-b’-bx=-ab’-b+ba’-a⇒a’-ay-b’-bx=ba’-ab’
And, the diagonal passing through B a’, b and D a, b’ is
y-b=b’-ba-a’x-a’⇒a-a’y-ba-a’=b’-bx-a’b’-b⇒a-a’y-b’-bx=-a’b’-b+ba-a’⇒a’-ay+b’-bx=a’b’-ab
Hence, the equations of the diagonals are a’-ay-b’-bx=ba’-ab’ and a’-ay+b’-bx=a’b’-ab.
Q5.
Answer :
The vertices of triangle ABC are A (4, 3), B (0, 0) and C (2, 3).
Let us find the lengths of sides AB and AC.
AB=4-02+3-02=5AC=4-22+3-32=2
We know that the internal bisector AD of angle BAC divides BC in the ratio AB : AC i.e. 5 : 2
∴ D≡2×0+5×25+2, 2×0+5×35+2=107, 157
Thus, the equation of AD is
y-3=3-1574-107x-4⇒y-3=13x-4⇒x-3y+5=0
Q6.
Answer :
Let the given points be A (a, b), B (a’, b’), C (−a, b) and D (a’, −b’).
Let P and Q be the midpoints of AB and CD, respectively.
∴ P≡a+a’2, b+b’2Q≡a’-a2, b-b’2
The equation of the line passing through P and Q is
y-b+b’2=b-b’2-b+b’2a’-a2-a’+a2x-a+a’2⇒2y-b-b’=b’a2x-a-a’⇒2ay-2b’x=ab-a’b’
Hence, the equation of the required straight line is 2ay-2b’x=ab-a’b’
Q7.
Answer :
Let y − x + 2 = 0 divide the line joining the points (3, −1) and (8, 9) at point P in the ratio k : 1
∴ P≡3+8kk+1, -1+9kk+1
P lies on the line y − x + 2 = 0
∴-1+9kk+1-3+8kk+1+2=0⇒-1+9k-3-8k+2k+2=0⇒3k=2⇒k=23
Hence, the line y − x + 2 = 0 divides the line joining the points (3, −1) and (8, 9) in the ratio 2 : 3
Q8.
Answer :
Let the line 3x + y = 12 intersect the x-axis and the y-axis at A and B, respectively.
At x = 0
0 + y = 12
⇒y = 12
At y = 0
3x + 0 = 12
⇒x = 4
∴ A≡4, 0 and B≡0, 12
Let y=m1x and y=m2x be the lines that pass through the origin and trisect the line 3x + y = 12 at P and Q.
∴ AP = PQ = QB
Let us find the coordinates of P and Q.
P≡2×4+1×02+1, 2×0+1×122+1≡83, 4Q≡1×4+2×02+1, 1×0+2×122+1≡43, 8
Clearly, P and Q lie on y=m1x and y=m2x, respectively.
∴ 4=m1×83 and 8=m2×43⇒m1=32 and m2=6
Hence, the required lines are y=32x ⇒2y=3x and y=6x
Q9.
Answer :
The equation of the line joining the points (6, 8) and (−3, −2) is
y-8=-2-8-3-6x-6⇒10x-9y+12=0
Let 10x − 9y + 12 = 0 divide the line joining the points (2, 3) and (4, −5) at point P in the ratio k : 1
∴ P≡4k+2k+1, -5k+3k+1
P lies on the line 10x − 9y + 12 = 0
∴104k+2k+1-9-5k+3k+1+12=0⇒40k+20+45k-27+12k+12=0⇒ 97k+5=0⇒k=-597
Hence, the line joining the points (2, 3) and (4, −5) is divided by the line passing through the points (6, 8) and (−3, −2) in the ratio 5 : 97 externally.
Q10.
Answer :
The two diagonals of the quadrilateral with vertices A (−2, 6), B (1, 2), C (10, 4) and D (7, 8) are AC and BD.
The equation of AC passing through A (−2, 6) and C (10, 4) is
y-6=4-610+2x+2⇒x+6y-34=0
And, the equation of BD passing through B (1, 2) and D (7, 8) is
y-2=8-27-1x-1⇒x-y+1=0
Hence, the equations of the diagonals are x+6y-34=0 and x-y+1=0
Q11.
Answer :
Assuming C along the x-axis and L along the y-axis, we have two points, (20, 124.942) and (110, 125.134), in CL-plane.
As L is a linear function of C, the equation of the line passing through (20, 124.942) and (110, 125.134) is
L-124.942=125.134-124.942110-20C-20⇒L-124.942=0.19290C-20⇒L-124.942=0.03215C-20⇒L=0.03215C+124.942-20×0.03215⇒L=0.03215C+124.942-0.04267⇒L=41875C+124.899
Q12.
Answer :
Let x denote the price per litre and y denote the quantity of the milk sold at this price.
Since there is a linear relationship between the price and the quantity, the line representing this relationship passes through (14, 980) and (16, 1220).
So, the equation of the line passing through these points is
y-980=1220-98016-14x-14⇒y-980=120x-14⇒120x-y-700=0
When x = 17 then we have,
120×17-y-700=0⇒y=1340
Hence, the owner of the milk store can sell 1340 litres of milk at Rs 17 per litre.
Q13.
Answer :
The vertices of triangle ABC are A (−1, −2), B (0, 1) and C (2, 0).
So, the equation of BC is
y-1=0-12-0x-0⇒y-1=-12x-0⇒2y-2=-x⇒x+2y-2=0
Let D be the midpoint of BC.
∴ D≡0+22, 1+02≡1, 12
So, the equation of median AD is
y+2=12+21+1x+1y+2=54x+1⇒4y+8=5x+5⇒5x-4y-3=0
Q14.
Answer :
Let the given points be A (−2, −2), B (8, 2) and C (3, 0).
The equation of the line passing through A (−2, −2) and B (8, 2) is
y+2=2+28+2x+2⇒y+2=25x+2⇒5y+10=2x+4⇒2x-5y-6=0
Clearly, point C (3, 0) satisfies the equation 2x-5y-6=0
Hence, the given points are collinear.
Page 23.40 Ex 23.6
Q1.
Answer :
(i) Here, a = 3, b = 2
So, the equation of the line is
xa+yb=1⇒x3+y2=1⇒2x+3y-6=0
(ii) Here, a = -5, b = 6
So, the equation of the line is
xa+yb=1⇒x-5+y6=1⇒6x-5y+30=0
Q2.
Answer :
The equation of the line cutting off equal intercepts ‘a’ on the coordinate is
xa+yb=1⇒xa+ya=1⇒x+y=a
The line x + y = a passes through (1, −2)
∴ 1-2=a⇒a=-1
Hence, the equation of the line is x+y=-1
Q3.
Answer :
(i) Here, a = b
So, the equation of the line is
xa+yb=1⇒xa+ya=1⇒x+y=a
The line x + y = a passes through (5, 6).
∴ 5+6=a⇒a=11
Hence, the equation of the line is x+y=11
(ii) Here, b = -a
So, the equation of the line is
xa+yb=1⇒xa+y-a=1⇒x-y=a
The line x – y = a passes through (5, 6).
∴ 5-6=a⇒a=-1
Hence, the equation of the line is x-y=-1
Q4.
Answer :
The equation of the line with intercepts a and b is xa+yb=1
This line intersects the axes at A (a, 0) and B (0, b).
Here, (α, β) is the midpoint of AB.
∴ α=a+02, β=0+b2⇒a=2α, b=2β
Hence, the equation of the line is x2α+y2β=1
Q5.
Answer :
The equation of the line with intercepts a and b is xa+yb=1.
The line intersects the axes at A (a, 0) and B (0, b).
Let O be the origin.
It is given that the area of the triangle formed by the coordinate axes and the line is 6 square units.
∴ Area of ∆OAB=12OA×OB⇒6=12ab
⇒ab=12
⇒ab=3×4 … (1)
Here, the length of the hypotenuse is 5 units, i.e. AB = 5.
∴OA2+OB2=AB2
⇒a2+b2=25 … (2)
Let us find the possible values of a and b from (1) and (2).
Using equation (1)
144b2+b2=25⇒b4-25b2+144=0⇒b2=16, 9⇒b=±4, ±3
Now, from equation (1)
For b=±4, a=3⇒b=4,a=3,-3 and b=-4, a=3, -3
For b=±3, a=4⇒b=3,a=4,-4 and b=-3, a=4, -4
Hence, the possible equations of the lines are
x3+y4=1, x-3+y4=1, x3+y-4=1, x-3+y-4=1, x4+y3=1, x-4+y3=1, x4+y-3=1 and x-4+y-3=1
or 4x + 3y = 12 or 4x – 3y = -12 or -4x + 3y = -12 or -4x – 3y = 12 or 3x + 4y = 12 or x – 4y = -12 or -3x + 4y = -12 or -3x – 4y = 12
Q6.
Answer :
The equation of the line with intercepts a and b is xa+yb=1.
Here, a + b = 7
⇒b = 7 − a … (1)
The line passes through (−3, 8).
∴ -3a+8b=1 … (2)
Substituting b = 7 − a in (2) we get,
-3a+87-a=1⇒-37-a+8a=7a-a2⇒a2+4a-21=0⇒a-3a+7=0⇒a=3, a≠-7 ∵ a is positive
Substituting a = 3 in (1) we get,
b = 7 − 3 = 4
Hence, the equation of the line is x3+y4=1 or 4x + 3y = 12
Q7.
Answer :
The equation of the line with intercepts a and b is xa+yb=1
The line xa+yb=1 intersects the axes at (a, 0) and (0, b).
So, (−4, 3) divides the line segment AB in the ratio 5 : 3
∴ -4=5×0+3×a5+3, 3=5×b+3×05+3⇒3a=-32, 5b=24⇒a=-323, b=245
Thus, the equation of the required line is
x-323+y245=1⇒3x-32+5y24=1⇒9x-20y+96=0
Q8.
Answer :
The equation of the line with intercepts a and b is xa+yb=1
Here, a = b + 5 … (1)
The line passes through (22, −6).
∴ 22a-6b=1 … (2)
Substituting a = b + 5 from equation (1) in equation (2)
22b+5-6b=1⇒22b-6b-30=b2+5b⇒b2-11b+30=0⇒b-5b-6=0⇒b=5, 6
From equation (1)
When b = 5 then, a = 5 + 5 = 10
When b = 6 then, a = 6 + 5 = 11
Thus, the equation of the required line is
x10+y5=1 or x11+y6=1⇒x+2y-10=0 or 6x+11y-66=0
Q9.
Answer :
The equation of the line with intercepts a and b is xa+yb=1.
Since the line meets the coordinate axes at A and B, so the coordinates are A (a, 0) and B (0, b).
Given:
4AP-3BP=0⇒AP : BP=3 : 4
Here, P≡1, -7
∴ 1=3×0+4×a3+4, -7=3×b+4×03+4⇒4a=7, 3b=-49⇒a=74, b=-493
Thus, the equation of the line is
x74+y-493=1
⇒4×7-3y49=1⇒28x-3y=49
Q10.
Answer :
The equation of the line with intercepts a and b is xa+yb=1.
Here, a + b = 9
⇒b=9-a … (1)
The line passes through (2, 2).
∴ 2a+2b=1 … (2)
From equations (1) and (2)
2a+29-a=1⇒18-2a+2a=9a-a2⇒a2-9a+18=0⇒a-3a-6=0⇒a=3, 6
For a = 3, b = 9 – 3 = 6
For a = 6, b = 9 – 6 = 3
Thus, the equation of the line is
x3+y6=1 or x6+y3=1⇒2x+y=6 or x+2y=6
Q11.
Answer :
The equation of the line with intercepts a and b is xa+yb=1.
The line passes through R (h, k).
∴ ha+kb=1 … (1)
The line intersects the coordinate axes at A (a, 0) and B (0, b).
Here, AP : PB = 1 : 2
∴ h=1×0+2×a1+2, k=1×b+2×01+2⇒a=3h2, b=3k
Substituting a=3h2, b=3k in xa+yb=1
2x3h+y3k=1⇒2kx+hy-3hk=0
Hence, the equation of the line is 2kx+hy-3hk=0
Q12.
Answer :
The equation of the line with intercepts a and b is xa+yb=1
Since, the line meets the coordinate axes at A and B, the coordinates of A and B are A (a, 0) and B (0, b).
Given:
AP : BP=2 : 3
Here, P≡2, 6
∴ 2=2×0+3×a2+3, 6=2×b+3×02+3⇒3a=10, 2b=30⇒a=103, b=15
Thus, the equation of the line is
x103+y15=1⇒3×10+y15=1⇒9x+2y=30
Q13.
Answer :
The equation of the line with intercepts a and b is xa+yb=1
Here, a − b = 2
⇒a = b + 2 … (1)
The line passes through (3, 2).
∴ 3a+2b=1 … (2)
Substituting a = b + 2 in equation (2)
3b+2+2b=1⇒3b+2b+4=b2+2b⇒b2-3b-4=0⇒b-4b+1=0⇒b=4, -1
Now, from equation (1)
For b = 4, a = 4 + 2 = 6
For b = − 1, a = − 1 + 2 = 1
Thus, the equations of the lines are
x1+y-1=1 and x6+y4=1⇒x-y=1 and 2x+3y=12
Q14.
Answer :
Let the line 2x + 3y = 6 intersect the x-axis and the y-axis at A and B, respectively.
At x = 0 we have,
0 + 3y = 6
⇒ y = 2
At y = 0 we have,
2x + 0 = 6
⇒ x = 3
∴ A≡3, 0 and B≡0, 2
Let y=m1x and y=m2x pass through the origin trisecting the line 2x + 3y = 6 at P and Q.
∴ AP = PQ = QB
Let us find the coordinates of P and Q using the section formula.
P≡2×3+1×02+1, 2×0+1×22+1=2, 23Q≡1×3+2×02+1, 1×0+2×22+1=1, 43
Clearly, P and Q lie on y=m1x and y=m2x, respectively.
∴ 23=m1×2 and 43=m2×1⇒m1=13 and m2=43
Hence, the required lines are
y=13x and y=43x
⇒ x − 3y = 0 and 4x − 3y = 0
Q15.
Answer :
The equation of the line in intercept form is xa+yb=1.
The line passes through (2, 1).
∴ 2a+1b=1 … (1)
Let the line 3x − 5y = 15 intersect the x-axis and the y-axis at A and B, respectively.
At x = 0 we have,
0 − 5y = 15
⇒ y = −3
At y = 0, we have,
3x − 0 = 15
⇒ x = 5
∴ A≡0, -3 and B≡5, 0
The midpoint of AB is 52,-32.
Clearly, the point 52,-32 lies on the line xa+yb=1.
∴ 52a-32b=1 … (2)
Using 32×eq (1)+eq (2) we get,
3a+52a=32+1⇒a=115
For a = 115 we have,
1011+1b=1⇒b=11
Hence, the equation of the required line is
Q16.
Answer :
The equation of the line with intercepts a and b is xa+yb=1.
Since the line meets the coordinate axes at A and B, the coordinates are A (a, 0) and B (0, b).
Let the given point be P (3, 4).
Here, AP : BP=2 : 3
∴ 3=2×0+3×a2+3, 4=2×b+3×02+3⇒3a=15, 2b=20⇒a=5, b=10
Hence, the equation of the line is
x5+y10=1⇒2x+y=10
Q17.
Answer :
The equation of the line passing through the origin is y = mx.
Let the line ax + by + c = 0 meet the coordinate axes at A and B.
So, the coordinates of A and B are A -ca, 0 and B 0, -cb.
Now, the midpoint of AB is -c2a, -c2b.
Clearly, -c2a, -c2b lies on the line y = mx.
∴-c2b=m×-c2a⇒m=ab
Hence, the equation of the required line is
y=abx⇒ax-by=0
Q18.
Answer :
The equation of the line with intercepts a and b is xa+yb=1.
Here, a = b and ab = 25
∴a×a=25⇒a2=25⇒a=5 ∵we are to take only positive value of intercepts
Hence, the equation of the required line is
x5+y5=1⇒x+y=5
Page 23.45 Ex 23.7
Q1.
Answer :
(i) Here, p = 5, α = 60°
So, the equation of the line in normal form is
xcos60∘+ysin60∘=5⇒x2+3y2=5⇒x+3y=10
(ii) Here, p = 4, α = 150°
So, the equation of the line in normal form is
xcos150∘+ysin150∘=4⇒xcos180°-30∘+ysin180°-30∘=4⇒-xcos30∘+ysin30∘=4⇒-3×2+y2=4⇒3x-y+8=0
(iii) Here, p = 8, α = 225°
So, the equation of the line in normal form is
xcos225∘+ysin225∘=8⇒xcos180∘+45∘+ysin180∘+45∘=8⇒-xcos45∘-ysin45∘=8⇒-x2-y2=8⇒x+y+82=0
(iv) p = 8, α = 300°
So, the equation of the line in normal form is
xcos300∘+ysin300∘=8⇒xcos360∘-60∘+ysin360∘-60∘=8⇒xcos60∘-ysin60∘=8⇒x2-3y2=8⇒x-3y=16
Q2.
Answer :
Here, p = 3, α=tan-1512
∴ tanα=512⇒sinα=513 and cosα=1213
So, the equation of the line in normal form is
xcosα+ysinα=p⇒12×13+5y13=3⇒12x+5y=39
Q3.
Answer :
Here, p = 2, sinα=13
∴ cosα=1-sin2α⇒cosα=1-19 =223
So, the equation of the line in normal form is
xcosα+ysinα=p⇒22×3+y3=2⇒22x+y=6
Q4.
Answer :
Let the perpendicular drawn from the origin make acute angle α with the positive x-axis.
Then, we have,
tanα=512
Here, tan180∘+α=tanα
So, there are two possible lines, AB and CD, on which the perpendicular drawn from the origin has slope equal to 512.
Now, tanα=512⇒sinα=513 and cosα=1213
Here, p = 2
So, the equations of the lines in normal form are
xcosα+ysinα=p and xcos180∘+α+ysin180∘+α=p⇒xcosα+ysinα=2 and -xcosα-ysinα=2⇒12×13+5y13=2 and -12×13-5y13=2⇒12x+5y=26 and 12x+5y=-26
Q5.
Answer :
Let AB be the given line which make an angle of 1500 with the positive
direction of y-axis and OQ be the perpendicular drawn from the origin on the line.
Here, p = 7 and α=30∘
So, the equation of the line AB is
xcosα+ysinα=p ⇒xcos30∘+ysin30°=7⇒3×2+y2=7⇒3x+y=14
Q6.
Answer :
Let AB be the given line and OL = p be the perpendicular drawn from the origin on the line.
Here, α=60∘
So, the equation of the line AB is
xcosα+ysinα=p ⇒xcos60∘+ysin60∘=p⇒x2+3y2=p⇒x+3y=2p … (1)
Now, in triangles OLA and OLB
cos60∘=OLOA and cos30∘=OLOB⇒12=pOA and 32=pOB⇒OA=2p and OB=2p3
It is given that the area of triangle OAB is 963
∴ 12×OA×OB=963⇒12×2p×2p3=963⇒p2=122⇒p=12
Substituting the value of p in (1)
x+3y=24
Hence, the equation of the line AB is x+3y=24
Q7.
Answer :
Here, p = 4, α=15∘
Now, cos15∘=cos45∘-30∘=cos45∘cos30∘+sin45∘sin30∘⇒cos15∘=12×32+12×12=3+122
And, sin15∘=sin45∘-30∘=sin45∘cos30∘-cos45∘sin30∘⇒sin15∘=12×32-12×12=3-122
So, the equation of the line in normal form is
xcosα+ysinα=p⇒3+1×22+3-1y22=4⇒3+1x+3-1y=82
Q8.
Answer :
Let AB be the given line and OL = p be the perpendicular drawn from the origin on the line.
Here, α=30∘
So, the equation of the line AB is
xcosα+ysinα=p ⇒xcos30∘+ysin30∘=p⇒3×2+y2=p⇒3x+y=2p … (1)
Now, in triangles OLA and OLB
cos30∘=OLOA and cos60∘=OLOB⇒32=pOA and 12=pOB⇒OA=2p3 and OB=2p
It is given that the area of triangle OAB is 50/3
∴ 12×OA×OB=503⇒12×2p3×2p=503⇒p2=25⇒p=5
Substituting the value of p in (1):
3x+y=10
Hence, the equation of the line AB is x+3y=10.
Q9.
Answer :
The normal form of a line is
x cos θ + y sin θ = p … (1)
Let us try to write down the equation 3x+y+2=0 in its normal form.
Now, 3x+y+2=0⇒3x+y=-2⇒-32x-y2=1 Dividing both sides by -2⇒-32x+-12y=1 … (2)
Comparing equations (1) and (2) we get,
cosθ=-32, and p=1⇒θ=210∘=7π6 and p=1
Page 23.53 Ex 23.8
Q1.
Answer :
Here, x1, y1=3, 2, tanθ=34 and r = 5 units
Now, sinθ=332+42 and cosθ=432+42⇒sinθ=35 and cosθ=45
So, the equation of the line is x-3cosθ=y-2sinθ
⇒x-345=y-235⇒x-34=y-23⇒3x-9=4y-8⇒3x-4y=1
Hence, the points on the line at a distance of 5 units from A (3, 2) are
x1±rcosθ, y1±rsinθ
3±5×45, 2±5×35 or 3±4, 2±3or 7, 5 and -1, -1
Q2.
Answer :
Here, x1, y1=A 1, 2, θ=60∘
So, the equation of the line is
x-x1cosθ=y-y1sinθ=r⇒x-1cos60∘=y-2sin60∘=r⇒x-112=y-232=rHere, r represents the distance of any point on this line from point A (1, 2). The coordinates of any point P on this line are 1+r2, 2+3r2.
Clearly, P lies on the line x + y = 6
∴1+r2+2+3r2=6⇒3r2+r2=3⇒r3+1=6⇒r=63+1=33-1
Q3.
Answer :
Here, x1, y1=A1, 2
Let P be the point of intersection of both the lines.
∴ AP = r = 23
Let θ be the slope of the line. So, the equation of the line that has slope θ and passes through A (1, 2) is
x-x1cosθ=y-y1sinθ⇒x-1cosθ=y-2sinθ
The coordinates of P are given by
x-1cosθ=y-2sinθ=r=23⇒x=1+23cosθ, y=2+23sinθ
Thus, the coordinates of P are 1+23cosθ, 2+23sinθ.
Clearly, P lies on the line x + y = 4.
1+23cosθ+ 2+23sinθ=4⇒cosθ+sinθ=32⇒cos2θ+sin2θ+2sinθcosθ=32 Squaring both sides ⇒sin2θ=32-1=12⇒2θ=30∘ or 150∘⇒θ=15∘ or 75∘
Hence, the direction of the lines with the positive direction of the x-axis is 15∘ or 75∘.
Q4.
Answer :
Here, x1, y1=A 2, 3, θ=45∘
So, the equation of the line passing through (2, 3) and making an angle of 45° with the x-axis is
x-x1cosθ=y-y1sinθ⇒x-2cos45∘=y-3sin45∘⇒x-112=y-212⇒x-y+1=0
Let x − y + 1 = 0 intersect the line 2x − 3y + 9 = 0 at point P.
Let AP = r
Then, the coordinates of P are given by
x-2cos45°=y-3sin45°=r
⇒x=2+r2 and y=3+r2
Thus, the coordinates of P are 2+r2, 3+r2.
Clearly, P lies on the line 2x − 3y + 9 = 0.
∴ 22+r2-33+r2+9=0⇒4+2r2-9-3r2+9=0⇒r2=4⇒r=42
Hence, the distance of the point from the given line is 42.
Q5.
Answer :
Here, x1, y1=A3, 5, tanθ=12⇒sinθ=112+22 and cosθ=212+22⇒ sinθ=15 and cosθ=25
So, the equation of the line passing through (3, 5) and having slope 12 is
x-x1cosθ=y-y1sinθ⇒x-325=y-515⇒x-2y+7=0
Let x − 2y + 7 = 0 intersect the line 2x + 3y = 14 at point P.
Let AP = r
Then, the coordinates of P are given by
x-325=y-515=r
⇒x=3+2r5 and y=5+r5
Thus, the coordinates of P are 3+2r5, 5+r5.
Clearly, P lies on the line 2x + 3y = 14.
∴ 23+2r5+35+r5=14⇒6+4r5+15+3r5=14⇒7r5=-7⇒r=-5
Hence, the distance of the point (3, 5) from the line 2x + 3y = 14 is 5.
Q6.
Answer :
Here, x1, y1=A 2, 5, tanθ=34⇒sinθ=332+42 and cosθ=432+42⇒ sinθ=35 and cosθ=45
So, the equation of the line passing through A (2, 5) and having slope 34 is
x-x1cosθ=y-y1sinθ⇒x-245=y-535⇒3x-6=4y-20⇒3x-4y+14=0
Let 3x − 4y + 14 = 0 intersect the line 3x + y + 4 = 0 at point P.
Let AP = r
Then, the coordinates of P are given by
x-245=y-535=r
⇒x=2+4r5 and y=5+3r5
Thus, the coordinates of P are 2+4r5, 5+3r5.
Clearly, P lies on the line 3x + y + 4 =0.
∴ 32+4r5+5+3r5+4=0⇒6+12r5+5+3r5+4=0⇒3r=-15⇒r=-5
Hence, the distance of the point (2, 5) from the line 3x + y + 4 = 0 is 5.
Q7.
Answer :
The slope of the line 3x − 4y + 1 = 0 or y=34x-14 is 34
So, the slope of the required line is also 34 as it is parallel to the given line.
∴ tanθ=34⇒sinθ=35 and cosθ=45
Here, x1, y1=A 4, -1
So, the equation of the line passing through A (4, −1) and having slope 34 is
x-x1cosθ=y-y1sinθ⇒x-445=y+135⇒3x-12=4y+4⇒3x-4y-16=0
Here, AP = r = 5
Thus, the coordinates of P are given by
x=x1±rcosθ, y=y1±rsinθ⇒x=4±545, y=-1±535
⇒x=4±4, y=-1±3⇒x=8, y=2 and x=0, y=-4
Hence, the coordinates of the two points at a distance of 5 units from A are (8, 2) and (0, −4).
Q8.
Answer :
Here, x1, y1=A 2, 1, θ=π4
So, the equation of the line passing through A (2, 1) is
x-x1cosθ=y-y1sinθ⇒x-2cos45∘=y-1sin45∘⇒x-212=y-112⇒x-y-1=0
Let AB = r
Thus, the coordinates of B are given by
x-2cos45°=y-1sin45°=r
⇒x=2+r2, y=1+r2
Clearly, point B 2+r2, 1+r2 lies on the line x + 2y + 1 = 0.
∴ 2+r2+21+r2+1=0⇒5+3r2=0⇒r=-523
Hence, the length of AB is 523.
Q9.
Answer :
Let P1P2 be the intercept between the lines 5x − y − 4 = 0 and 3x + 4y − 4 = 0.
Let P1P2 make an angle θ with the positive x-axis.
Here, x1, y1=A 1, 5
So, the equation of the line passing through A (1, 5) is
x-x1cosθ=y-y1sinθ⇒x-1cosθ=y-5sinθ⇒y-5x-1=tanθ
Let AP1=AP2=r
Then, the coordinates of P1 and P2 are given by
x-1cosθ=y-5sinθ=r and x-1cosθ=y-5sinθ=-r
So, the coordinates of P1 and P2 are 1+rcosθ, 5+rsinθ and 1-rcosθ, 5-rsinθ, respectively.
Clearly, P1 and P2 lie on 5x − y − 4 = 0 and 3x + 4y − 4 = 0, respectively.
∴ 51+rcosθ-5-rsinθ-4=0 and 31-rcosθ+45-rsinθ-4=0⇒r=45cosθ-sinθ and r=193cosθ+4sinθ⇒45cosθ-sinθ =193cosθ+4sinθ⇒95cosθ-19sinθ=12cosθ+16sinθ⇒83cosθ=35sinθ⇒tanθ=8335
Thus, the equation of the required line is
y-5x-1=tanθ⇒y-5x-1=8335⇒83x-35y+92=0
Q10.
Answer :
Here, x1, y1=P 3, 4, θ=π6=30∘
So, the equation of the line is
x-x1cosθ=y-y1sinθ⇒x-3cos30∘=y-4sin30∘⇒x-332=y-412⇒x-3y+43-3=0
Let PQ = r
Then, the coordinates of Q are given by
x-3cos30°=y-4sin30°=r
⇒x=3+3r2, y=4+r2
Thus, the coordinates of Q are 3+3r2, 4+r2.
Clearly, the point Q lies on the line 12x + 5y + 10 = 0.
∴123+3r2+5 4+r2+10=0⇒66+123+52r=0⇒r=-1325+123
∴ PQ = r = 1325+123
Q11.
Answer :
Here, x1, y1=A-2, -7
So, the equation of the line is
x-x1cosθ=y-y1sinθ⇒x+2cosθ=y+7sinθ
Let the required line intersect the lines 4x + 3y = 3 and 4x + 3y = 12 at P1 and P2.
Let AP1 = r1 and AP2 = r2
Then, the coordinates of P1 and P2 are given by x+2cosθ=y+7sinθ=r1 and x+2cosθ=y+7sinθ=r2, respectively.
Thus, the coordinates of P1 and P2 are -2+r1cosθ, -7+r1sinθ and -2+r2cosθ, -7+r2sinθ, respectively.
Clearly, the points P1 and P2 lie on the lines 4x + 3y = 3 and 4x + 3y = 12
4-2+r1cosθ+3-7+r1sinθ=3 and 4-2+r2cosθ+3-7+r2sinθ=12⇒r1=324cosθ+3sinθ and r2=414cosθ+3sinθ
Here, AP2-AP1=3⇒r2-r1=3⇒414cosθ+3sinθ-324cosθ+3sinθ=3⇒3=4cosθ+3sinθ⇒31-sinθ=4cosθ⇒91+sin2θ-2sinθ=16cos2θ=161-sin2θ⇒25sin2θ-18sinθ-7=0⇒sinθ-125sinθ+7=0⇒sinθ=1, sinθ=-725⇒ cosθ=0, cosθ=2425
Thus, the equation of the required line is
x+2=0 or x+22425=y+7-725⇒x+2=0 or 7x+24y+182=0
Q12.
Answer :
Here, x1, y1=A 3, 5
It is given that the required line is parallel to x − 2y = 1
⇒2y=x-1⇒y=12x-12
∴ tanθ=12⇒sinθ=15, cosθ=25
So, the equation of the line is
x-x1cosθ=y-y1sinθ⇒x-325=y-515⇒x-3=2y-10⇒x-2y+7=0
Let line x-2y+7=0 cut line 2x + 3y = 14 at P.
Let AP = r
Then, the coordinates of P are given by
x-325=y-515=r
⇒x=3+2r5, y=5+r5
Thus, the coordinates of P are 3+2r5, 5+r5.
Clearly, P lies on the line 2x + 3y = 14.
∴ 23+2r5+3 5+r5=14⇒7+7r5=0⇒r=-5
∴ AP = r = 5
Q13.
Answer :
Here, x1, y1=A2, 5
It is given that the required line is parallel to 3x −4y + 8 = 0
⇒4y=3x+8⇒y=34x+2
∴ tanθ=34⇒sinθ=35, cosθ=45
So, the equation of the line is
x-x1cosθ=y-y1sinθ⇒x-245=y-535⇒3x-6=4y-20⇒3x-4y+14=0
Let the line 3x-4y+14=0 cut the line 3x + y + 4 = 0 at P.
Let AP = r
Then, the coordinates of P are given by
x-245=y-535=r
⇒x=2+4r5, y=5+3r5
Thus, the coordinates of P are 2+4r5, 5+3r5.
Clearly, P lies on the line 3x + y + 4 = 0.
∴ 32+4r5+ 5+3r5+4=0⇒ 6+12r5+ 5+3r5+4=0⇒15+15r5=0⇒r=-5
∴ AP = r = 5
Q14.
Answer :
Here, x1, y1=A-1, -3 and tanθ=1⇒sinθ=12, cosθ=12
So, the equation of the line is
x-x1cosθ=y-y1sinθ⇒x+112=y+312⇒x+1=y+3⇒x-y-2=0
Let line x-y-2=0 cut line 2x + y = 3 at P.
Let AP = r
Then, the coordinates of P are given by
x+1cosθ=y+3sinθ=r
⇒x=-1+rcosθ, y=-3+rsinθ
⇒x=-1+r2, y=-3+r2
Thus, the coordinates of P are -1+r2, -3+r2
Clearly, P lies on the line 2x + y = 3.
∴ 2-1+r2-3+r2=3⇒-2-2r-3+r2=3⇒3r2=8⇒r=823
∴ AP = 823
Q15.
Answer :
The equation of the line that passes through P x1, y1 and makes an angle of θ with the x-axis is x-x1cosθ=y-y1sinθ.
Let PQ = r
Then, the coordinates of Q are given by
x=x1+rcosθ, y=y1+rsinθ
Thus, the coordinates of Q are x1+rcosθ, y1+rsinθ.
Clearly, Q lies on the line ax + by + c = 0.
∴ ax1+rcosθ+b y1+rsinθ+c=0⇒r=-ax1+by1+cacosθ+bsinθ
∴ PQ = ax1+by1+cacosθ+bsinθ
Page 23.58 Ex 23.9
Q1.
Answer :
(i) 3x + y + 2 = 0
⇒y=-3x-2
This is the slope intercept form of the given line.
Here, slope = -3 and y-intercept = -2
(ii) 3x + y + 2 = 0
⇒3x+y=-2⇒3x-2+y-2=1 Dividing both sides by -2⇒x-23+y-2=1
This is the intercept form of the given line.
Here, x-intercept = -23 and y-intercept = -2
(iii) 3x + y + 2 = 0
⇒-3x-y=2⇒-3x-32+-12-y-32+-12=2-32+-12 Dividing both sides by coefficient of x2+coefficient of y2⇒-3×2-y2=1
This is the normal form of the given line.
Here, p = 1, cosα=-32 and sinα=-12
⇒α=210∘
Q2.
Answer :
The given equation is xa+yb=1
bx+ay=ab⇒ay=-bx+ab⇒y=-bax+b
This is the slope intercept form of the given line.
∴ Slope = -ba and y-intercept = b
Q3.
Answer :
The given equation is 3x − 2y + 6 = 0
3x-2y=-6⇒3-6x+2y6=1 Dividing both sides by -6⇒x-2+y3=1
This is the intercept form of the given line.
∴ x-intercept = −2 and y-intercept = 3
Q4.
Answer :
Let c be the intercept on the y-axis.
Then, the equation of the line is
y=-x+c ∵m=-1⇒x+y=c⇒x12+12+y12+12=c12+12 Dividing both sides by coefficient of x2+coefficient of y2⇒x2+y2=c2
This is the normal form of the given line.
Therefore, c2 denotes the length of the perpendicular from the origin.
But, the length of the perpendicular is 5 units.
∴ c2=5⇒c=±52
Thus, substituting c=±52 in y=-x+c, we get the equation of line to be y=-x+52 or, x+y-52=0
Q5.
Answer :
(i) x+3y-4=0
⇒x+3y=4⇒x12+32+3y12+32=412+32 Dividing both sides by coefficient of x2+coefficient of y2⇒x2+3y2=2
This is the normal form of the given line, where p = 2, cosα=12 and sinα=32⇒α=π3.
(ii) x+y+2=0
⇒-x-y=2⇒-x-12+-12-y-12+-12=2-12+-12 Dividing both sides by coefficient of x2+coefficient of y2⇒-x2-y2=1
This is the normal form of the given line, where p = 1, cosα=-12 and
sinα=-12⇒α=225∘ ∵ The coefficent of x and y are negative.So, α lies in third quadrant
(iii) x-y+22=0
⇒-x+y=22⇒-x-12+12+y-12+12=22-12+12 Dividing both sides by coefficient of x2+coefficient of y2⇒-x2+y2=2
This is the normal form of the given line, where p = 2, cosα=-12 and
sinα=12⇒α=135∘ ∵ The coefficent of x and y are negative and positive respectively.So, α lies in second quadrant.
(iv) x − 3 = 0
⇒x=3⇒x+0×y=3⇒x12+02+0×y12+02=312+02 Dividing both sides by coefficient of x2+coefficient of y2⇒x+0×y=3
This is the normal form of the given line, where p = 3, cosα=1 and sinα=0⇒α=0.
(v) y − 2 = 0
⇒y=2⇒0×x+y=2⇒0×x02+12+y02+12=202+12 Dividing both sides by coefficient of x2+coefficient of y2⇒0×x+y=2
This is the normal form of the given line, where p = 2, cosα=0 and sinα=1⇒α=90∘.
Q6.
Answer :
Let us write down the normal forms of the lines 3x − 4y + 4 = 0 and 2x + 4y − 5 = 0.
⇒-3x+4y=4⇒-3-32+42x+4-32+42y=4-32+42 Dividing both sides by coefficient of x2+coefficient of y2⇒-35x+45y=45 … (1)
Now, 2x + 4y = − 5
⇒-2x-4y=5
⇒-222+42x-422+42y=522+42 Dividing both sides by coefficient of x2+coefficient of y2⇒-225x-425y=525 … (2)
From equations (1) and (2):
45<525
Hence, the line 3x − 4y + 4 = 0 is nearer to the origin.
Q7.
Answer :
Let us write down the normal forms of the given lines.
First line: 4x + 3y + 10 = 0
⇒-4x-3y=10⇒-4-42+-32x-3-42+-32y=10-42+-32 Dividing both sides by coefficient of x2+coefficient of y2⇒-45x-35y=2 ∴ p=2
Second line: 5x − 12y + 26 = 0
⇒-5x+12y=26⇒-5-52+122x+12-52+122y=26-52+122 Dividing both sides by coefficient of x2+coefficient of y2⇒-513x+1213y= 2∴ p=2
Third line: 7x + 24y = 50
⇒772+242x+2472+242y=5072+242 Dividing both sides by coefficient of x2+coefficient of y2⇒725x+2425y=2∴ p=2
Hence, the origin is equidistant from the given lines.
Q8.
Answer :
The normal form of the line 3x+y+2=0 is
-3x-y=2⇒-3-32+-12x-1-32+-12y=2-32+-12 Dividing both sides by coefficient of x2+coefficient of y2⇒-32x-12y=1
Comparing the equations xcos θ + ysin θ = p and -32x-12y=1 we get,
cosθ=-32, sinθ=-12 and p=1
∴ θ=210∘ and p=1
Page 23.64 Ex 23.10
Q1.
Answer :
(i)
The equations of the lines are as follows:
2x − y + 3 = 0 … (1)
x + y − 5 = 0 … (2)
Solving (1) and (2) using cross-multiplication method:
x5-3=y3+10=12+1⇒x2=y13=13⇒x=23 and y=133
Hence, the point of intersection is 23,133.
(ii)
The equations of the lines are as follows:
bx + ay = ab
⇒ bx + ay − ab = 0 … (1)
ax + by = ab
⇒ax + by − ab = 0 … (2)
Solving (1) and (2) using cross-multiplication method:
x-a2b+ab2=y-a2b+ab2=1b2-a2⇒xabb-a=yabb-a=1a+bb-a⇒x=aba+b and y=aba+b
Hence, the point of intersection is aba+b, aba+b.
(iii)
The equations of the lines are y=m1 x+am1 and y=m2 x+am2.
Thus, we have:
m1 x-y+am1=0 … (1)
m2 x-y+am2=0 … (2)
Solving (1) and (2) using cross-multiplication method:
x-am2+am1=yam2m1-am1m2=1-m1+m2⇒x=-am2+am1-m1+m2, y=am2m1-am1m2-m1+m2⇒x=am1m2 and y=am1+m2m1m2
Hence, the point of intersection is am1m2, am1+m2m1m2 or am1m2, a1m1+1m2.
Page 23.65 Ex 23.10
Q2.
Answer :
(i) x + y − 4 = 0, 2x − y + 3 = 0 and x − 3y + 2 = 0
x + y − 4 = 0 … (1)
2x − y + 3 = 0 … (2)
x − 3y + 2 = 0 … (3)
Solving (1) and (2) using cross-multiplication method:
x3-4=y-8-3=1-1-2⇒x=13, y=113
Solving (1) and (3) using cross-multiplication method:
x2-12=y-4-2=1-3-1⇒x=52, y=32
Similarly, solving (2) and (3) using cross-multiplication method:
x-2+9=y3-4=1-6+1⇒x=-75, y=15
Hence, the coordinates of the vertices of the triangle are 13, 113, 52, 32 and -75, 15.
(ii) y (t1 + t2) = 2x + 2a t1t2, y (t2 + t3) = 2x + 2a t2t3 and y (t3 + t1) = 2x + 2a t1t3
2x − y (t1 + t2) + 2a t1t2 = 0 … (1)
2x − y (t2 + t3) + 2a t2t3 = 0 … (2)
2x − y (t3 + t1) + 2a t1t3 = 0 … (3)
Solving (1) and (2) using cross-multiplication method:
x-2at2t3t1+t2+2at1t2t2+t3=y4at1t2-4at2t3=1-2t2+t3+2t1+t2⇒x2at22t1-t3=y4at2t1-t3=12t1-t3⇒x=at22, y=2at2
Solving (1) and (3) using cross-multiplication method:
x-2at1t3t1+t2+2at1t2t3+t1=y4at1t2-4at1t3=1-2t3+t1+2t1+t2⇒x2at12t2-t3=y4at1t2-t3=12t2-t3⇒x=at12, y=2at1
Similarly, solving (2) and (3) using cross-multiplication method:
x-2at1t3t2+t3+2at2t3t3+t1=y4at2t3-4at1t3=1-2t3+t1+2t2+t3⇒x2at32t2-t1=y4at3t2-t1=12t2-t1⇒x=at32, y=2at3
Hence, the coordinates of the vertices of the triangle are at12, 2at1, at22, 2at2 and at32, 2at3.
Q3.
Answer :
(i) y = m1x + c1 … (1)
y = m2x + c2 … (2)
x = 0 … (3)
In triangle ABC, let equations (1), (2) and (3) represent the sides AB, BC and CA, respectively.
Solving (1) and (2):
x=c2-c1m1-m2, y=m1c2-m2c1m1-m2
Thus, AB and BC intersect at B c2-c1m1-m2,m1c2-m2c1m1-m2.
Solving (1) and (3):
x=0, y=c1
Thus, AB and CA intersect at A 0,c1.
Similarly, solving (2) and (3):
x=0, y=c2
Thus, BC and CA intersect at C 0,c2.
∴ Area of triangle ABC = 120c110c21c2-c1m1-m2m1c2-m2c1m1-m21
= 12c2-c1m1-m2c1-c2=12c1-c22m2-m1
(ii) y = 0 … (1)
x = 2 … (2)
x + 2y = 3 … (3)
In triangle ABC, let equations (1), (2) and (3) represent the sides AB, BC and CA, respectively.
Solving (1) and (2):
x = 2, y = 0
Thus, AB and BC intersect at B (2, 0).
Solving (1) and (3):
x = 3, y = 0
Thus, AB and CA intersect at A (3, 0).
Similarly, solving (2) and (3):
x = 2, y = 12
Thus, BC and CA intersect at C 2, 12.
∴ Area of triangle ABC = 122013012121=14
(iii) x + y − 6 = 0 … (1)
x − 3y − 2 = 0 … (2)
5x − 3y + 2 = 0 … (3)
In triangle ABC, let equations (1), (2) and (3) represent the sides AB, BC and CA, respectively.
Solving (1) and (2):
x = 5, y = 1
Thus, AB and BC intersect at B (5, 1).
Solving (1) and (3):
x = 2, y = 4
Thus, AB and CA intersect at A (2, 4).
Similarly, solving (2) and (3):
x = −1, y = −1
Thus, BC and CA intersect at C (−1, −1).
∴ Area of triangle ABC = 12511241-1-11=12
Q4.
Answer :
The given equations are as follows:
3x + 2y + 6 = 0 … (1)
2x − 5y + 4 = 0 … (2)
x − 3y − 6 = 0 … (3)
In triangle ABC, let equations (1), (2) and (3) represent the sides AB, BC and CA, respectively.
Solving (1) and (2):
x = −2, y = 0
Thus, AB and BC intersect at B (−2, 0).
Solving (1) and (3):
x = -611, y = -2411
Thus, AB and CA intersect at A -611, -2411.
Similarly, solving (2) and (3):
x = −42, y = −16
Thus, BC and CA intersect at C (−42, −16).
Let D, E and F be the midpoints the sides BC, CA and AB, respectively.Then,
Then, we have:
D=-2-422, 0-162=-22, -8
E=-611-422, -2411-162=-23411, -10011
F=-611-22, -2411+02=-1411, -1211
Now, the equation of median AD is
y+2411=-8+2411-22+611x+611⇒16x-59y-120=0
The equation of median BE is
y-0=-10011-0-23411+2x+2⇒25x-53y+50=0
And, the equation of median CF is
y+16=-1211+16-1411+42x+42⇒41x-112y-70=0
Q5.
Answer :
The given equations are as follows:
y=3x+1 … (1)
y = 4 … (2)
y=-3x+2 … (3)
In triangle ABC, let equations (1), (2) and (3) represent the sides AB, BC and CA, respectively.
Solving (1) and (2):
x=3, y = 4
Thus, AB and BC intersect at B 3, 4.
Solving (1) and (3):
x=123, y=32
Thus, AB and CA intersect at A 123, 32.
Similarly, solving (2) and (3):
x=-23, y=4
Thus, BC and AC intersect at C -23, 4.
Now, we have:
AB=123-32+32-42=53BC=3+232+4-42=53AC=123+232+32-42=53
Hence, the given lines form an equilateral triangle.
Q6.
Answer :
Let a1x+b1y+c1=0 and a2x+b2y+c2=0 be the two lines.
(a) The lines intersect if a1a2≠b1b2 is true.
(b) The lines are parallel if a1a2=b1b2≠c1c2 is true.
(c) The lines are coincident if a1a2=b1b2=c1c2 is true.
(i) 2x + y − 1 = 0 and 3x + 2y + 5 = 0
Here, 23≠12
Therefore, the lines 2x + y − 1 = 0 and 3x + 2y + 5 = 0 intersect.
(ii) x − y = 0 and 3x − 3y + 5 = 0
Here, 13=-1-3≠05
Therefore, the lines x − y = 0 and 3x − 3y + 5 = 0 are parallel.
(iii) 3x + 2y − 4 = 0 and 6x + 4y − 8 = 0
Here, 36=24=-4-8
Therefore, the lines 3x + 2y − 4 = 0 and 6x + 4y − 8 = 0 are coincident.
Q7.
Answer :
We have,
4x + y − 1 = 0 … (1)
7x − 3y − 35 = 0 … (2)
Solving (1) and (2) using cross-multiplication method:
x-35-3=y-7+140=1-12-7⇒x=2, y=-7
Thus, the point of intersection of the given lines is 2,-7.
So, the equation of the line joining the points (3, 5) and 2, -7 is
y-5=-7-52-3x-3⇒y-5=12x-36⇒12x-y-31=0
Q8.
Answer :
We have,
4x − 7y − 3 = 0 … (1)
2x − 3y + 1 = 0 … (2)
Solving (1) and (2) using cross-multiplication method:
x-7-9=y-6-4=1-12+14⇒x=-8, y=-5
Thus, the point of intersection of the given lines is -8, -5.
Now, the equation of a line having equal intercept as a is xa+ya=1.
This line passes through -8, -5.
∴-8a-5a=1⇒-8-5=a⇒a=-13
Hence, the equation of the required line is x-13+y-13=1 or x+y+13=0.
Q9.
Answer :
The given lines are as follows:
y = m1 x … (1)
y = m2 x … (2)
y = c … (3)
Solving (1) and (2), we get (0, 0) as their point of intersection.
Solving (1) and (3), we get cm1, c as their point of intersection.
Similarly, solving (2) and (3), we get cm2, c as their point of intersection.
∴ Area of the triangle formed by these lines = 12001cm1c1cm2c1=12c2m1-c2m2=c22m2-m1m1m2
It is given that m1 and m2 are the roots of the equation x2+3+2x+3-1=0.
∴ m1+m2=-3+2, m1m2=3-1⇒m2-m1=m1+m22-4m1m2⇒m2-m1=-3+22-43+4⇒m2-m1=7+43-43+4=11
∴ Area=c22113-1=c223+1113+13-1 =c2233+112=c2433+11
Q10.
Answer :
The given lines are x + y = 3 and 2x − 3y = 1.
x + y − 3 = 0 … (1)
2x − 3y − 1 = 0 … (2)
Solving (1) and (2) using cross-multiplication method:
x-1-9=y-6+1=1-3-2⇒x=2, y=1
Thus, the point of intersection of the given lines is (2, 1).
It is given that the line xa+yb=1 passes through (2, 1).
∴ 2a+1b=1 … (3)
It is also given that the line xa+yb=1 is parallel to the line x − y − 6 = 0.
Hence, Slope of xa+yb=1 ⇒y=-bax+b is equal to the slope of x − y − 6 = 0 or, y = x − 6
∴-ba=1
⇒b=-a … (4)
From (3) and (4):
2a-1a=1⇒a=1
From (4):
b = −1
∴ a = 1, b = −1
Q11.
Answer :
The given lines are as follows:
x + y = 1 … (1)
2x + 3y = 6 … (2)
4x − y + 4 = 0 … (3)
In triangle ABC, let equations (1), (2) and (3) represent the sides AB, BC and CA, respectively.
Solving (1) and (2):
x = −3, y = 4
Thus, AB and BC intersect at B (−3, 4).
Solving (1) and (3):
x = -35 , y = 85
Thus, AB and CA intersect at A -35, 85.
Let AD and BE be the altitudes.
AD⊥BC and BE⊥AC
∴ Slope of AD × Slope of BC = −1
and Slope of BE × Slope of AC = −1
Here, slope of BC = slope of the line (2) = -23 and slope of AC = slope of the line (3) = 4
∴ Slope of AD×-23=-1 and slope of BE×4=-1⇒Slope of AD=32 and slope of BE=-14
The equation of the altitude AD passing through A -35, 85 and having slope 32 is
y-85=32x+35
⇒3x-2y+5=0 … (4)
The equation of the altitude BE passing through B (−3, 4) and having slope -14 is
y-4=-14x+3
⇒x+4y-13=0 … (5)
Solving (4) and (5), we get 37, 227 as the orthocentre of the triangle.
Q12.
Answer :
The sides AB, BC and CA of a triangle ABC are as follows:
5x − 3y + 2 = 0 … (1)
x − 3y − 2 = 0 … (2)
x + y − 6 = 0 … (3)
Solving (1) and (3):
x = 2 , y = 4
Thus, AB and CA intersect at A (2, 4).
Let AD be the altitude.
AD⊥BC
∴ Slope of AD × Slope of BC = −1
Here, slope of BC = slope of the line (2) = 13
∴ Slope of AD×13=-1 ⇒Slope of AD=-3
Hence, the equation of the altitude AD passing through A (2, 4) and having slope −3 is
y-4=-3x-2⇒3x+y=10
Q13.
Answer :
Let A (0, 0), B (−1, 3) and C (2, −1) be the vertices of the triangle ABC.
Let AD and BE be the altitudes.
AD⊥BC and BE⊥AC
∴ Slope of AD × Slope of BC = −1
Slope of BE × Slope of AC = −1
Here, slope of BC = -1-32+1=-43
and slope of AC = -1-02-0=-12
∴Slope of AD×-43=-1 and slope of BE×-12=-1 ⇒Slope of AD=34and slope of BE=2
The equation of the altitude AD passing through A (0, 0) and having slope 34 is
y-0=34x-0⇒y=34x …. (1)
The equation of the altitude BE passing through B (−1, 3) and having slope 2 is
y-3=2x+1⇒2x-y+5=0 …. (2)
Solving (1) and (2):
x = − 4, y = − 3
Hence, the coordinates of the orthocentre is (−4, −3).
Q14.
Answer :
The given lines are as follows:
3x − 4y = 0 … (1)
12y + 5x = 0 … (2)
y − 15 = 0 … (3)
In triangle ABC, let equations (1), (2) and (3) represent the sides AB, BC and CA, respectively.
Solving (1) and (2):
x = 0, y = 0
Thus, AB and BC intersect at B (0, 0).
Solving (1) and (3):
x = 20 , y = 15
Thus, AB and CA intersect at A (20, 15).
Solving (2) and (3):
x = −36 , y = 15
Thus, BC and CA intersect at C (−36, 15).
Let us find the lengths of sides AB, BC and CA.
AB=20-02+15-02=25BC=0+362+0-152=39AC=20+362+15-152=56
Here, a = BC = 39, b = CA = 56 and c = AB = 25
Also, x1, y1 = A (20, 15), x2, y2 = B (0, 0) and x3, y3 = C (−36, 15)
∴ Centroid=x1+x2+x33, y1+y2+y33 =20+0-363, 15+0+153=-163, 10
And, incentre=ax1+bx2+cx3a+b+c, ay1+by2+cy3a+b+c =39×20+56×0-25×3639+56+25, 39×15+56×0+25×1539+56+25 =-120120, 120×8120=-1, 8
Q15.
Answer :
The given lines are as follows:
3x+y=0 … (1)
3y+x=0 … (2)
3x+y=1 … (3)
3y+x=1 … (4)
In quadrilateral ABCD, let equations (1), (2), (3) and (4) represent the sides AB, BC, CD and DA, respectively.
Lines (1) and (3) are parallel and lines (2) and (4) are parallel.
Solving (1) and (2):
x = 0, y = 0.
Thus, AB and BC intersect at B (0, 0).
Solving (1) and (4):
x = -12 , y = 32
Thus, AB and DA intersect at A -12, 32.
Solving (3) and (2):
x = 32 , y = -12
Thus, BC and CD intersect at C 32, -12.
Solving (3) and (4):
x = 3-12 , y = 3-12
Thus, DA and CD intersect at D 3-12, 3-13.
Let us find the lengths of sides AB, BC and CD and DA.
AB=0-122+0-322=1BC=32-02+-12-02=1CD=3-12-322+3-12+122=1DA=3-12+122+3-12-322=1
Hence, the given lines form a rhombus.
Page 23.70 Ex 23.11
Q1.
Answer :
(i) Given:
15x − 18y + 1 = 0 … (1)
12x + 10y − 3 = 0 … (2)
6x + 66y − 11 = 0 … (3)
Now, consider the following determinant:
15-1811210-3666-11=15-110+198+18-132+18+1792-60
⇒15-1811210-3666-11=1320-2052+732=0
Hence, the given lines are concurrent.
(ii)
Given:
3x − 5y − 11 = 0 … (1)
5x + 3y − 7 = 0 … (2)
x + 2y = 0 … (3)
Now, consider the following determinant:
3-5-1153-7120=3×14+5×7-11×7=0
Hence, the given lines are concurrent.
(iii)
Given:
bx+ay-ab=0 … (1)
ax+by-ab=0 … (2)
x − y = 0 … (3)
Now, consider the following determinant:
ba-abab-ab1-10=-b×ab-a×ab-ab×-a-b=0
Hence, the given lines are concurrent.
Q2.
Answer :
Given:
2x − 5y + 3 = 0 … (1)
5x − 9y + λ = 0 … (2)
x − 2y + 1 = 0 … (3)
It is given that the three lines are concurrent.
∴ 2-535-9λ1-21=0⇒2-9+2λ+55-λ+3-10+9=0⇒-18+4λ+25-5λ-3=0⇒λ=4
Q3.
Answer :
The given lines can be written as follows:
m1x-y+c1=0 … (1)
m2x-y+c2=0 … (2)
m3x-y+c3=0 … (3)
It is given that the three lines are concurrent.
∴ m1-1c1m2-1c2m3-1c3=0⇒m1-c3+c2+1m2c3-m3c2+c1-m2+m3=0⇒m1c2-c3+m2c3-c1+m3c1-c2=0
Hence, the required condition is m1c2-c3+m2c3-c1+m3c1-c2=0.
Q4.
Answer:
The given lines can be written as follows:
p1 x + q1 y – 1 = 0 … (1)
p2 x + q2 y – 1 = 0 … (2)
p3 x + q3 y – 1 = 0 … (3)
It is given that the three lines are concurrent.
∴ p1q1-1p2q2-1p3q3-1=0⇒-p1q11p2q21p3q31=0⇒p1q11p2q21p3q31=0
This is the condition for the collinearity of the three points, (p1, q1), (p2, q2) and (p3, q3).
Q5.
Answer :
The given lines can be written as follows:
(b + c) x + ay + 1 = 0 … (1)
(c + a) x + by + 1 = 0 … (2)
(a + b) x + cy + 1 = 0 … (3)
Consider the following determinant.
b+ca1c+ab1a+bc1
Applying the transformation C1→C1+C2 ,
b+ca1c+ab1a+bc1=a+b+ca1c+a+bb1a+b+cc1
⇒b+ca1c+ab1a+bc1 = a+b+c1a11b11c1
⇒b+ca1c+ab1a+bc1 =0
Hence, the given lines are concurrent.
Q6.
Answer :
The given lines can be written as follows:
ax + a2y + 1 = 0 … (1)
bx + b2y + 1 = 0 … (2)
cx + c2y + 1 = 0 … (3)
The given lines are concurrent.
∴ aa21bb21cc21=0
Applying the transformation R1→R1-R2 and R2→R2-R3:
a-ba2-b20b-cb2-c20cc21=0⇒a-bb-c1a+b01b+c0cc21=0⇒a-bb-cc-a=0
⇒a-b=0 or b-c=0 or c-a=0⇒a=b or b=c or c=a
Therefore, atleast two of the constants a,b,c are equal .
Q7.
Answer :
The given lines can be written as follows:
ax + 2y + 1 = 0 … (1)
bx + 3y + 1 = 0 … (2)
cx + 4y + 1 = 0 … (3)
Consider the following determinant.
a21b31c41
Applying the transformation R1→R1-R2 and R2→R2-R3,
a21b31c41=a-b-10b-c-10c41
⇒a21b31c41=-a+b+b-c=2b-a-c
Given:
2b = a + c
a21b31c41=a+c-a-c=0
Hence, the given lines are concurrent, provided 2b = a + c.
Q8.
Answer :
Let ABC be a triangle with vertices A x1, y1, B x2, y2 and C x3, y3.
Let D, E and F be the midpoints of the sides BC, CA and AB, respectively.
Thus, the coordinates of D, E and F are D x2+x32, y2+y32, E x1+x32, y1+y32 and F x1+x22, y1+y22.
Let mD, mE and mF be the slopes of AD, BE and CF respectively.
∴ Slope of BC × mD = -1
⇒y3-y2x3-x2×mD=-1⇒mD=-x3-x2y3-y2
Thus, the equation of AD
y-y2+y32=-x3-x2y3-y2x-x2+x32
⇒y-y2+y32=-x3-x2y3-y2x-x2+x32⇒2yy3-y2-y32-y22=-2xx3-x2+x32-x22
⇒2xx3-x2+2yy3-y2-x32-x22-y32-y22=0 … (1)
Similarly, the respective equations of BE and CF are
2xx1-x3+2yy1-y3-x12-x32-y12-y32=0 … (2)
2xx2-x1+2yy2-y1-x22-x12-y22-y12=0 … (3)
Let L1, L2 and L3 represent the lines (1), (2) and (3), respectively.
Adding all the three lines,
We observe:
1·L1+1·L2 +1·L3=0
Hence, the perpendicular bisectors of the sides of a triangle are concurrent.
Page 23.79 Ex 23.12
Q1.
Answer :
The equation of the line parallel to 3x − 4y + 5 = 0 is 3x-4y+λ=0, where λ is a constant.
It passes through (2, 3).
∴6-12+λ=0⇒λ=6
Hence, the required line is 3x − 4y + 6 = 0.
Q2.
Answer :
The equation of the line perpendicular to x − 3y + 5 = 0 is 3x+y+λ=0, where λ is a constant.
It passes through (3, −2).
9-2+λ=0⇒λ=-7
Substituting λ = −7 in 3x+y+λ=0, we get 3x+y-7=0, which is the required line.
Q3.
Answer :
Let A (1, 3) and B (3, 1) be the given points.
Let C be the midpoint of AB.
∴Coordinates of C=1+32, 3+12 =2, 2
Slope of AB=1-33-1=-1∴ Slope of the perpendicular bisector of AB=1
Thus, the equation of the perpendicular bisector of AB is
y-2=1x-2⇒x-y=0
or, y=x
Q4.
Answer :
The vertices of ∆ABC are A (1, 4), B (−3, 2) and C (−5, −3).
Slope of AB = 2-4-3-1=12
Slope of BC = -3-2-5+3=52
Slope of CA = 4+31+5=76
Thus, we have:
Slope of CF = -2
Slope of AD = -25
Slope of BE = -67
Hence,
Equation of CF is :y+3=-2x+5⇒2x+y+13=0Equation of AD is : y-4=-25x-1 ⇒2x+5y-22=0Equation of BE is : y-2=-67x+3⇒6x+7y+4=0
Q5.
Answer :
The line perpendicular to 3x-y+5=0 is x+3y+λ=0.
It is given that the line x+3y+λ=0 cuts off an intercept of 4 units with the negative direction of the y-axis.
This means that the line passes through 0,-4.
∴ 0-3×4+λ=0⇒λ=43
Substituting the value of λ, we get x+3y+43=0, which is the equation of the required line.
Q6.
Answer :
The line perpendicular to 3x-y+5=0 is x+3y+λ=0
It is given that the line x+3y+λ=0 is at a distance of 3 units from the origin.
∴ λ1+3=3⇒λ=±6
Substituting the value of λ, we get x+3y±6=0, which is equation of the required line.
Q7.
Answer :
The line perpendicular to lx + my + n = 0 is mx-ly+λ=0
This line passes through (α, β).
∴ mα-lβ+λ=0⇒λ=lβ-mα
Substituting the value of λ:
mx-ly+lβ-mα=0⇒mx-α=ly-β
This is equation of the required line.
Q8.
Answer :
The line perpendicular to 2x − 3y = 5 is 3x+2y+λ=0
It is given that the line 3x+2y+λ=0 cuts off an intercept of 1 on the positive direction of the x-axis.
This means that the line 3x+2y+λ=0 passes through the point (1, 0).
∴ 3+0+λ=0⇒λ=-3
Substituting the value of λ, we get 3x+2y-3=0, which is equation of the required line.
Q9.
Answer :
The line perpendicular to 5x − 2y = 8 is 2x+5y+λ=0
Coordinates of the mid points of 2,3 and 4,5=2+42, 3+52
= (3,4)
∴ 6+20+λ=0⇒λ=-26
Substituting the value of λ, we get 2x+5y-26=0, which is equation of the required line.
Q10.
Answer :
The line perpendicular to 3x − 4y + 11 = 0 is 4x+3y+λ=0
It is given that the line 4x+3y+λ=0 has y-intercept equal to 43
This means that the line passes through 0, 43
∴ 0+4+λ=0⇒λ=-4
Substituting the value of λ, we get 4x+3y-4=0, which is equation of the required line.
Q11.
Answer :
Let A (a, b) and B (a1, b1) be the given points. Let C be the midpoint of AB.
∴Coordinates of C=a+a12, b+b12
And, slope of AB = b1-ba1-a
So, the slope of the right bisector of AB is -a1-ab1-b
Thus, the equation of the right bisector of the line segment joining the points (a, b) and (a1, b1) is
y-b+b12=-a1-ab1-bx-a+a12⇒2a1-ax+2yb1-b+a2+b2-a12+b12=0 This is equation of the required line .
Q12.
Answer :
Let the image of A (2, 1) be B (a, b). Let M be the midpoint of AB.
∴ Coordinates of M are≡2+a2, 1+b2
The point M lies on the line x + y − 5 = 0
∴ 2+a2+1+b2-5=0
⇒a+b=7 … (1)
Now, the lines x + y − 5 = 0 and AB are perpendicular.
∴ Slope of AB × Slope of CD = −1
⇒b-1a-2×-1=-1⇒a-2=b-1
⇒ a-b=1 … (2)
Adding eq (1) and eq (2):
2a=8⇒a=4
Now, from equation (1):
4+b=7⇒b=3
Hence, the image of the point (2, 1) with respect to the line mirror x + y − 5 = 0 is (4, 3).
Q13.
Answer :
Let the image of A (2, 1) be B (5, 2). Let M be the midpoint of AB.
∴Coordinates of M=2+52, 1+22 =72, 32
Let CD be the mirror.
The line AB is perpendicular to the mirror CD.
∴ Slope of AB × Slope of CD = −1
⇒2-15-2×Slope of CD=-1⇒Slope of CD=-3
Thus, the equation of the mirror CD is
y-32=-3x-72⇒2y-3=-6x+21⇒6x+2y-24=0⇒3x+y-12=0
Page 23.80 Ex 23.12
Q14.
Answer :
Let the given points be A (2, 3) and B (4, −1). Let M be the midpoint of AB.
∴Coordinates of M=2+42, 3-1 2 =3, 1
The equation of the line parallel to 3x − 4y + 6 = 0 is 3x-4y+λ=0
This line passes through M (3,1).
∴9-4+λ=0⇒λ=-5
Substituting the value of λ in 3x-4y+λ=0, we get 3x-4y-5=0, which is the equation of the required line.
Q15.
Answer :
The given lines can be written as
y=23x+13 … (1)
y=-x+3 … (2)
y=23x-23 … (3)
y=-x+4 … (4)
The slope of lines (1) and (3) is 23 and that of lines (2) and (4) is −1.
Thus, lines (1) and (3), and (2) and (4) are two pair of parallel lines.
If both pair of opposite sides are parallel then ,we can say that it is a parallelogram.
Hence, the given lines form a parallelogram.
Q16.
Answer :
Let us find the intersection of the line x4+y6=1 with y-axis.
At x = 0,
0+y6=1⇒y=6
Thus, the given line intersects y-axis at (0, 6).
The line perpendicular to the line x4+y6=1 is
x6-y4+λ=0
This line passes through (0, 6).
0-64+λ=0⇒λ=32
Now, substituting the value of λ, we get:
x6-y4+32=0⇒2x-3y+18=0
This is the equation of the required line.
Q17.
Answer :
The given line is y = mx + c which can be written as
mx-y+c=0 … (1)
The slope of the line perpendicular to y = mx + c is -1m
So, the equation of the line with slope -1m and passing through the origin is
y=-1mx
x+my=0 … (2)
Solving eq (1) and eq (2) by cross multiplication, we get
xmc-0=y0-c=1-1-m2⇒x=-mcm2+1, y=cm2+1
Thus, the point of intersection of the perpendicular from the origin to the line y = mx + c is -mcm2+1, cm2+1
It is given that the perpendicular from the origin to the line y = mx + c meets it at the point (-1,2)
-mcm2+1=-1 and cm2+1=2⇒m2+1=mc and m2+1=c2⇒mc=c2⇒m=12
Now, substituting the value of m in m2+1=mc, we get
14+1=12c⇒c=52
Hence, m=12 and c=52.
Q18.
Answer :
Let A (3, 4) and B (−1, 2) be the given points.
Let C be the midpoint of AB.
∴C≡3-12, 4+22≡1, 3
∵Slope of AB=2-4-1-3=12∴ Slope of the perpendicular bisector of AB=-2
Thus, the equation of the perpendicular bisector of AB is
y-3=-2x-1⇒2x+y-5=0
Hence, the required line is 2x+y-5=0.
Q19.
Answer :
Let A (h,3) and B (4,1) be the given points.
The line 7x − 9y − 19 = 0 can be written as
y=79x-199
So, the slope of this line is 79
It is given that the line joining the points A (h,3) and B (4,1) is perpendicular to the line 7x − 9y − 19 = 0.
79×1-34-h=-1⇒9h-36=-14⇒9h=22⇒h=229
Hence, the value of h is 229.
Q20.
Answer :
Let the image of A (3,8) be B (a,b). Also, let M be the midpoint of AB.
∴Coordinates of M=3+a2, 8+b2
Point M lies on the line x + 3y = 7
∴3+a2+3×8+b2=7
⇒a+3b+13=0 … (1)
Lines CD and AB are perpendicular.
∴ Slope of AB × Slope of CD = −1
⇒b-8a-3×-13=-1⇒b-8=3a-9
⇒3a-b-1=0 … (2)
Solving (1) and (2) by cross multiplication, we get:
a-3+13=b39+1=1-1-9⇒a=-1, b=-4
Hence, the image of the point (3, 8) with respect to the line mirror x + 3y = 7 is (−1, −4).
Q21.
Answer :
Let A (−1, 3) be the given point.
Also, let M (h, k) be the foot of the perpendicular drawn from A (−1, 3) to the line 3x − 4y − 16 = 0
Point M (h, k) lies on the line 3x − 4y − 16 = 0
3h − 4k − 16 = 0 … (1)
Lines 3x − 4y − 16 = 0 and AM are perpendicular.
∴ k-3h+1×34=-1
⇒4h+3k-5=0 … (2)
Solving eq (1) and eq (2) by cross multiplication, we get:
h20+48=k-64+15=19+16⇒a=6825, b=-4925
Hence, the coordinates of the foot of perpendicular are 6825, -4925.
Q22.
Answer :
Let A (−1, 2) be the given point whose projection is to be evaluated and C (−1, 2) and D (5, 4) be the other two points.
Also, let M (h, k) be the foot of the perpendicular drawn from A (−1, 2) to the line joining the points C (−1, 2) and D (5, 4).
Clearly, the slope of CD and MD are equal.
Q23.
Answer :
Let the image of A (2, 1) be B (5, 2). Also, let M be the midpoint of AB.
∴Coordinates of M =2+52, 1+22 =72, 32
Let CD be the mirror.
Line AB is perpendicular to the mirror CD.
∴ Slope of AB × Slope of CD = −1
⇒2-15-2×Slope of CD=-1⇒Slope of CD=-3
Equation of the mirror CD:
y-32=-3x-72⇒2y-3=-6x+21⇒6x+2y-24=0⇒3x+y-12=0
Q24.
Answer :
The given line is 2x + 3y = 12, which can be written as
x6+y4=1 … (1)
So, the coordinates of the points A and B are (6, 0) and (0, 4), respectively.
The equation of the line perpendicular to line (1) is
x4-y6+λ=0
This line passes through the point (5, 5).
∴54-56+λ=0⇒λ=-512
Now, substituting the value of λ in x4-y6+λ=0, we get:
x4-y6-512=0⇒x53-y52=1 …(2)
Thus, the coordinates of intersection of line (1) with the x-axis is C 53,0.
To find the coordinates of E, let us write down equations (1) and (2) in the following manner:
2x+3y-12=0 … (3)
3x-2y-5=0 … (4)
Solving (3) and (4) by cross multiplication, we get:
x-15-24=y-36+10=1-4-9⇒x=3, y=2
Thus, the coordinates of E are (3, 2).
From the figure,
EC=53-32+0-22=2133
EA=6-32+0-22=13
Now,
Area OCEB=Area ∆OAB-Area ∆CAE⇒Area OCEB=12×6×4-12×2133×13 =233 sq units
Q25.
Answer :
Let the intercepts on x-axis and y-axis be 2a and a, respectively.
So, the equation of the line with intercepts 2a on x-axis and a on y-axis be
x2a+ya=1
⇒x+2y=2a … (1)
Let us change equation (1) into normal form.
x1+22+2y1+22=2a1+22×5+2y5=2a5
Thus, the length of the perpendicular from the origin to the line (1) is
p=2a5
Given:
p = 1
∴2a5=1⇒a=±52
Required equation of the line:
x+2y=±252⇒x+2y±5=0
Q26.
Answer :
Let the perpendicular bisectors x − y + 5 = 0 and x + 2y = 0 of the sides AB and AC intersect at D and E, respectively.
Let x1,y1 and x2,y2 be the coordinates of points B and C.
∴Coordinates of D=x1+12, y1-22 and coordinates of E=x2+12, y2-22
Point D lies on the line x − y + 5 = 0
∴x1+12-y1-22+5=0
⇒x1-y1+13=0 … (1)
Point E lies on the line x + 2y = 0
∴x2+12+2×y2-22=0
⇒x2+2y2-3=0 … (2)
Side AB is perpendicular to the line x − y + 5 = 0
∴ 1×y1+2×1-1=-1
⇒x1+y1+1=0 … (3)
Similarly, side AC is perpendicular to the line x + 2y = 0
∴ -12×y2+2×2-1=-1
⇒2×2-y2-4=0 … (4)
Now, solving eq (1) and eq (3) by cross multiplication, we get:
x1-1-13=y113-1=11+1⇒x1=-7, y1=6
Thus, the coordinates of B are -7,6.
Similarly, solving (2) and (4) by cross multiplication, we get:
x2-8-3=y2-6+4=1-1-4⇒x2=115, y2=25
Thus, coordinates of C are 115,25.
Therefore, equation of line BC is
y-6=25-6115+7x+7⇒y-6=-2846x+7⇒14x+23y-40=0
Page 23.85 Ex 23.13
Q1.
Answer :
(i) The equations of the lines are
3x + y + 12 = 0 … (1)
x + 2y − 1 = 0 … (2)
Let m1 and m2 be the slopes of these lines.
m1=-3, m2=-12
Let θ be the angle between the lines.
Then,
tanθ=m1-m21+m1m2 =-3+121+32 =1⇒θ=π4or 45°
Hence, the acute angle between the lines is 45°
(ii) The equations of the lines are
3x − y + 5 = 0 … (1)
x − 3y + 1 = 0 … (2)
Let m1 and m2 be the slopes of these lines.
m1=3, m2=13
Let θ be the angle between the lines.
Then,
tanθ=m1-m21+m1m2 =3-131+1 =43⇒θ=tan-143
Hence, the acute angle between the lines is tan-143.
(iii) The equations of the lines are
3x + 4y − 7 = 0 … (1)
4x − 3y + 5 = 0 … (2)
Let m1 and m2 be the slopes of these lines.
m1=-34, m2=43
∵m1m2=-34×43 =-1
Hence, the given lines are perpendicular.
Therefore, the angle between them is 90°.
(iv) The equations of the lines are
x − 4y = 3 … (1)
6x − y = 11 … (2)
Let m1 and m2 be the slopes of these lines.
m1=14, m2=6
Let θ be the angle between the lines.
Then,
tan θ=m1-m21+m1m2 =14-61+32 =2310⇒θ=tan-12310
Hence, the acute angle between the lines is tan-12310
(v) The equations of the lines are
(m2 − mn) y = (mn + n2) x + n3 … (1)
(mn + m2) y = (mn − n2) x + m3 … (2)
Let m1 and m2 be the slopes of these lines.
∴m1=mn+n2m2-mn, m2=mn-n2mn+m2
Let θ be the angle between the lines.
Then,
tan θ=m1-m21+m1m2 =mn+n2m2-mn-mn-n2mn+m21+mn+n2m2-mn×mn-n2mn+m2⇒tan θ=mn+n2mn+m2-mn-n2m2-mnm2-mnmn+m2+mn+n2mn-n2⇒tan θ=m2n2+m3n+mn3+m2n2-m3n+m2n2+m2n2-mn3m3n+m4-m2n2-m3n+m2n2-mn3+mn3-n4
⇒tanθ=4m2n2m4-n4
Hence, the acute angle between the lines is tan-14m2n2m4-n4.
Q2.
Answer :
The equations of the lines are
2x − y + 3 = 0 … (1)
x + y + 2 = 0 … (2)
Let m1 and m2 be the slopes of these lines.
m1=2, m2=-1
Let θ be the angle between the lines.
Then,
tan θ=m1-m21+m1m2 =2+11-2 =3⇒θ=tan-13
Hence, the acute angle between the lines is tan-13.
Q3.
Answer :
Let A(2, −1), B(0, 2), C(2, 3) and D(4, 0) be the vertices.
Slope of AB = 2+10-2=-32
Slope of BC = 3-22-0=12
Slope of CD = 0-34-2=-32
Slope of DA = -1-02-4=12
Thus, AB is parallel to CD and BC is parallel to DA.
Therefore, the given points are the vertices of a parallelogram.
Now, let us find the angle between the diagonals AC and BD.
Let m1 and m2 be the slopes of AC and BD, respectively.
∴ m1=3+12-2=∞m2=0-24-0=-12
Thus, the diagonal AC is parallel to the y-axis.
∴∠ODB=tan-112
In triangle MND,
∠DMN=π2-tan-112
Hence, the acute angle between the diagonal is π2-tan-112
Q4.
Answer :
Let A (2, 0), B (0, 3) be the given points.
Slope of AB = m1
= 3-00-2
=-32
Slope of the line x + y = 1 is -1
∴ m2=-1
Let θ be the angle between the line joining the points (2, 0), (0, 3) and the line x + y = 1
∴ tan θ=m1-m21+m1m2 =-32+11+32 =15⇒θ=tan-115
Hence, the acute angle between the line joining the points (2, 0), (0, 3) and the line x + y = 1 is tan-115
Q5.
Answer :
Let A (x1, y1) and B (x2, y2) be the given points.
Let O be the origin.
Slope of OA = m1 = y1x1
Slope of OB = m2 = y2x2
It is given that θ is the angle between lines OA and OB.
∴ tan θ=m1-m21+m1m2 =y1x1-y2x21+y1x1×y2x2⇒ tan θ=x2y1-x1y2x1x2+y1y2
Now,
As we know that cos θ=11+tan2 θ
∴cos θ=x1x2+y1y2x2y1-x1y22+x1x2+y1y22
⇒cos θ=x1x2+y1y2x22y12+x12y22+x12x22+y12y22
⇒cos θ=x1x2+y1y2x12+y12 x22+y22
Q6.
Answer :
The given lines are
(a + b) x + (a − b ) y = 2ab … (1)
(a − b) x + (a + b) y = 2ab … (2)
x + y = 0 … (3)
Let m1, m2 and m3 be the slopes of the lines (1), (2) and (3), respectively.
Now,
Slope of the first line = m1 = -a+ba-b
Slope of the second line = m2 = -a-ba+b
Slope of the third line = m3 = -1
Let θ1 be the angle between lines (1) and (2), θ2 be the angle between lines (2) and (3) and θ3 be the angle between lines (1) and (3).
∴tan θ1=m1-m21+m1m2 =-a+ba-b+a-ba+b1+a+ba-b×a-ba+b⇒tan θ1=2aba2-b2⇒θ1=tan-12aba2-b2 =2 tan-1ab
∴tan θ2=m2-m31+m2m3 =-a-ba+b+11+a-ba+b⇒tan θ2=ba⇒θ2=tan-1ba
∴tan θ3=m1-m31+m1m3 =-a+ba-b+11+a+ba-b⇒tan θ3=ba⇒θ3=tan-1ba
Here,
θ2=θ3 and θ=2 tan-1ab
Hence, the given lines form an isosceles triangle whose vertical angle is 2tan-1ab.
Q7.
Answer :
The given lines can be written as
x = a … (1)
y=-cb … (2)
Lines (1) and (2) are parallel to the y-axis and x-axis, respectively. Thus, they intersect at right angle, i.e. at 90°.
Q8.
Answer :
The respective equations of the lines having intercepts 3, 4 and 1, 8 on the axes are
x3+y4=1 … (1)
x1+y8=1 … (2)
Let m1 and m2 be the slope of the lines (1) and (2), respectively.
∴m1=-43, m2=-8
Let θ be the angle between the lines (1) and (2).
∴tan θ=m1-m21+m1m2 =-43+81+323⇒tan θ=47
Hence, the tangent of the angles between the lines is 47.
Q9.
Answer :
Let m1 be the slope of the line joining the points (a, 2a) and (−2, 3)
m1=3-2a-2-a
It is given that the line passing through points (a, 2a) and (−2, 3) is perpendicular to the line 4x + 3y + 5 = 0.
∴ m1×-43=-1⇒3-2a-2-a×-43=-1⇒8a-12=3a+6⇒a=185
Hence, the value of a is 185.
Q10.
Answer :
The given lines are
a2x + ay + 1 = 0 … (1)
x − ay = 1 … (2)
Let m1 and m2 be the slopes of the lines (1) and (2).
m1m2=-a2a×1a =-1
Hence, line a2x + ay + 1 = 0 is perpendicular to the line x − ay = 1 for all non-zero real values of a.
Page 23.89 Ex 23.14
Q1.
Answer :
Let ABC be the triangle of sides AB, BC and CA whose equations are x − 5y + 6 = 0, x − 3y + 2 = 0 and x − 2y − 3 = 0, respectively.
On solving the equations, we get A (9,3), B (4, 2) and C (13, 5) as the coordinates of the vertices.
It is given that point P (α2, α) lies either inside or on the triangle. The three conditions are given below.
(i) A and P must lie on the same side of BC.
(ii) B and P must lie on the same side of AC.
(iii) C and P must lie on the same side of AB.
If A and P lie on the same side of BC, then
9-9+2α2-3α+2≥0⇒α-2α-1≥0
⇒α∈(-∞,1]∪[2,∞) … (1)
If B and P lie on the same side of AC, then
4-4-3α2-2α-3≥0⇒α-3α+1≤0
⇒α∈-1,3 … (2)
If C and P lie on the same side of AB, then
13-25+6α2-5α+6≥0⇒α-3α-2≤0
⇒α∈2,3 … (3)
From (1), (2) and (3), we get:
α∈2,3
Q2.
Answer :
Let ABC be the triangle of sides AB, BC and CA whose equations are x + y − 4 = 0, 3x − 7y − 8 = 0 and 4x − y − 31 = 0, respectively.
On solving them, we get A 7,-3, B 185,25 and C 20925,6125 as the coordinates of the vertices.
Let P (a, 2) be the given point.
It is given that point P (a,2) lies inside the triangle. So, we have the following:
(i) A and P must lie on the same side of BC.
(ii) B and P must lie on the same side of AC.
(iii) C and P must lie on the same side of AB.
Thus, if A and P lie on the same side of BC, then
21+21-83a-14-8>0
⇒a>223 … (1)
If B and P lie on the same side of AC, then
4×185-25-314a-2-31>0
⇒a<334 … (2)
If C and P lie on the same side of AB, then
20925+6125-4a+2-4>0⇒345-4a+2-4>0
⇒a>2 … (3)
From (1), (2) and (3), we get:
a∈223,334
Q3.
Answer :
Let ABC be the triangle of sides AB, BC and CA, whose equations x + y − 4 = 0, 3x − 7y + 8 = 0 and 4x − y − 31 = 0, respectively.
On solving them, we get A7,-3, B (2, 2) and C (9, 5) as the coordinates of the vertices.
Let P (−3, 2) be the given point.
The given point P (−3, 2) will lie inside the triangle ABC, if
(i) A and P lies on the same side of BC
(ii) B and P lies on the same side of AC
(iii) C and P lies on the same side of AB
Thus, if A and P lie on the same side of BC, then
21+21+8-9-14+8>0⇒50×-15>0⇒-750>0, which is false
Therefore, the point (−3, 2) lies outside triangle ABC.
Page 23.94 Ex 23.15
Q1.
Answer :
Comparing ax + by + c = 0 and 3x − 5y + 7 = 0, we get:
a = 3, b = − 5 and c = 7
So, the distance of the point (4, 5) from the straight line 3x − 5y + 7 = 0 is
d=ax1+by1+ca2+b2⇒d=3×4-5×5+732+-52=634
Hence, the required distance is 634
Q2.
Answer :
The distance of the point (1, 1) from the straight line ax − by + c = 0 is 1
∴ 1=a-b+ca2+b2⇒a2+b2+c2-2ab+2ac-2bc=a2+b2⇒ab+bc-ac=c22
Dividing both the sides by abc, we get:
1c+1a-1b=c2ab
Q3.
Answer :
Equation of the line passing through (acosα, asinα) and (acosβ, asinβ) is
y-asinα=asinβ-asinαacosβ-acosαx-acosα⇒y-asinα=sinβ-sinαcosβ-cosαx-acosα⇒y-asinα=2cosβ+α2sinβ-α22sinβ+α2sinα-β2x-acosα⇒y-asinα=-cotβ+α2x-acosα⇒y-asinα=-cotα+β2x-acosα
⇒xcotα+β2+y-asinα-acosα cotα+β2=0
The distance of the line from the origin is
d=-asinα-acosα cotα+β2cot2α+β2+1⇒d=asinα+acosα cotα+β2cosec2α+β2 ∵cosec2θ=1+cot2θ
⇒d=asinα+β2sinα+cosα cosα+β2 ⇒d=asinα sinα+β2+cosα cosα+β2 ⇒d=acosα+β2-α =acosβ-α2=acosα-β2
Hence, the required distance is acosα-β2
Q4.
Answer :
et P(a, b) be any point on 2x + 11y − 5 = 0
∴ 2a + 11b − 5 = 0
⇒ b=5-2a11 …i
Let d1 and d2 be the perpendicular distances from point P
on the lines 24x + 7y = 20 and 4x − 3y − 2 = 0, respectively.
d1=24a+7b-20242+72=24a+7b-2025⇒d1=24a+7×5-2a11-2025 from (1)⇒d1=50a-3755
Similarly,
d2=4a-3b-232+-42=4a-3×5-2a11-25⇒d2=44a-15+6a-2211×5 from (1)⇒d2=50a-3755
∴ d1 = d2
Q5.
Answer :
Solving the lines 2x + 3y = 21 and 3x − 4y + 11 = 0 we get:
x33-84=y-63-22=1-8-9⇒x=3, y=5
So, the point of intersection of 2x + 3y = 21 and 3x − 4y + 11 = 0 is (3, 5).
Now, the perpendicular distance d of the line 8x + 6y + 5 = 0 from the point (3, 5) is
d=24+30+582+62=5910
Q6.
Answer :
Solving the lines 2x − 3y + 14 = 0 and 5x + 4y − 7 = 0 we get:
x21-56=y70+14=18+15⇒x=-3523, y=8423
So, the point of intersection of 2x − 3y + 14 = 0 and 5x + 4y − 7 = 0 is -3523,8423.
The equation of the line passing through the origin and the point -3523,8423 is
y-0=8423-0-3523-0x-0⇒y=84-35x⇒y=-125x⇒12x+5y=0
Let d be the perpendicular distance of the line 12x + 5y = 0 from the point (4, −7)
∴d=48-35122+52=1313=1
Q7.
Answer :
Let (t, 0) be a point on the x-axis.
It is given that the perpendicular distance of the line xa+yb=1 from a point is a.
∴ta+0-11a2+1b2=a⇒a21a2+1b2=t2a2+1-2ta⇒1+a2b2=t2a2+1-2ta⇒a2b2=t2a2-2ta
⇒b2t2-2ab2t-a4=0⇒t=2ab2±2a2b4+b2a42b2⇒t=abb±a2+b2
Hence, the required points on the x-axis are abb-a2+b2,0 and abb+a2+b2,0.
Q8.
Answer :
Let d1 and d2 be the perpendicular distances of line xa cos θ+yb sin θ=1 from points a2-b2,0 and -a2-b2,0, respectively.
∴d1=a2-b2acosθ-1cos2θa2+sin2θb2=b a2-b2cosθ-aa2sin2θ+b2cos2θ
Similarly,
d1=-a2-b2acosθ-1cos2θa2+sin2θb2=b -a2-b2cosθ-aa2sin2θ+b2cos2θ=b a2-b2cosθ+aa2sin2θ+b2cos2θ
Now,
d1d2=b a2-b2cosθ-aa2sin2θ+b2cos2θ×b a2-b2cosθ+aa2sin2θ+b2cos2θ⇒d1d2=b2 a2-b2cos2θ-a2a2sin2θ+b2cos2θ⇒d1d2=b2 a2cos2θ-1-b2cos2θa2sin2θ+b2cos2θ⇒d1d2=b2-a2sin2θ-b2cos2θa2sin2θ+b2cos2θ=b2a2sin2θ+b2cos2θa2sin2θ+b2cos2θ=b2
Q9.
Answer :
The equation of the line perpendicular to x-3y+4=0 is3x+y+λ=0.
This line passes through (1, 2).
∴3+2+λ=0⇒λ=-3-2
Substituting the value of λ, we get 3x+y-3-2=0
Let d be the perpendicular distance from the origin to the line 3x+y-3-2=0
d=0-0-3-21+3=3+22
Hence, the required perpendicular distance is 3+22
Q10.
Answer :
To find the point intersection of the lines x + 2y = 5 and x − 3y = 7, let us solve them.
x-14-15=y-5+7=1-3-2⇒x=295, y=-25
So, the equation of the line passing through 295,-25 with slope 5 is
y+25=5x-295⇒5y+2=25x-145⇒25x-5y-147=0
Let d be the perpendicular distance from the point (1, 2) to the line 25x-5y-147=0
∴d=25-10-147252+52=132526
Hence, the required perpendicular distance is 132526
Q11.
Answer :
Let (0, t) be a point on the y-axis.
It is given that the perpendicular distance of the line x3+y4=1 from the point (0, t) is 4 units.
∴0+t4-1132+142=4⇒t-4=4×4×53×4⇒t-4=203
⇒t-4=±203⇒t=4±203⇒t=4+203, 4-203⇒t=323, -83
Hence, the required points on the y-axis are 0,323 and 0,-83
Q12.
Answer :
The equation of the line joining the points (cos θ, sin θ) and (cos ϕ, sin ϕ) is given below:
y-sinθ=sinϕ-sinθcosϕ-cosθx-cosθ⇒cosϕ-cosθy-sinθcosϕ-cosθ=sinϕ-sinθx-sinϕ-sinθcosθ⇒sinϕ-sinθx-cosϕ-cosθy+sinθcosϕ-sinϕcosθ=0
Let d be the perpendicular distance from the origin to the line sinϕ-sinθx-cosϕ-cosθy+sinθcosϕ-sinϕcosθ=0
∴d=sinθcosϕ-sinϕcosθsinϕ-sinθ2+cosϕ-cosθ2⇒d=sinθ-ϕsin2ϕ+sin2θ-2sinϕsinθ+cos2ϕ+cos2θ-2cosϕcosθ⇒d=sinθ-ϕsin2ϕ+cos2ϕ+sin2θ+cos2θ-2cosθ-ϕ⇒d=12sinθ-ϕ1-cosθ-ϕ
⇒d=12sinθ-ϕ2sin2θ-ϕ2 ⇒d=12×2sinθ-ϕsinθ-ϕ2=122sinθ-ϕ2cosθ-ϕ2sinθ-ϕ2⇒d=cosθ-ϕ2
Hence, the required distance is cosθ-ϕ2.
Q13.
Answer :
Equation of side BC:
y+1=2+11-4x-4⇒x+y-3=0
The equation of the altitude that is perpendicular to x+y-3=0 is x-y+λ=0.
Line x-y+λ=0 passes through (2, 3).
∴2-3+λ=0⇒λ=1
Thus, the equation of the altitude from the vertex A (2, 3) is x-y+1=0.
Let d be the length of the altitude from A (2, 3).
d=2+3-312+12⇒d=2
Hence, the required distance is 2.
Q14.
Answer :
Let P(h, k) be the moving point such that it is equidistant from the lines 3x − 2y = 5 and 3x + 2y = 5
3h-2k-532+22=3h+2k-532+22⇒3h-2k-5=3h+2k-5⇒3h-2k-5=±3h+2k-5⇒3h-2k-5=3h+2k-5 and 3h-2k-5=-3h+2k-5⇒k=0 and 3h=5
Hence, the path of the moving points are 3x=5 or y=0 These are straight lines.
Q15.
Answer :
It is given that the sum of perpendicular distances of a variable point P (x, y) from the lines x + y − 5 = 0 and 3x − 2y + 7 = 0 is always 10
∴x+y-512+12+3x-2y+732+22=10⇒x+y-52+3x-2y+713=10
32+13x+13-22y+72-513-1026=0It is a straight line.
Page 23.99 Ex 23.16
Q1.
Answer :
(i) The parallel lines are
4x − 3y − 9 = 0 … (1)
4x − 3y − 24 = 0 … (2)
Let d be the distance between the given lines.
⇒d=-9+2442+-32=155=3 units
(ii) The parallel lines are
8x + 15y − 34 = 0 … (1)
8x + 15y + 31 = 0 … (2)
Let d be the distance between the given lines.
⇒d=-34-3182+152=6517 units
(iii) The given parallel lines can be written as
mx − y +c = 0 … (1)
mx − y +d = 0 … (2)
Let d be the distance between the given lines.
⇒d=c-dm2+1
(iv) The given parallel lines can be written as
4x + 3y − 11 = 0 … (1)
4x+3y-152=0 … (2)
Let d be the distance between the given lines.
⇒d=-11+15242+32=72×5=710 units
Q2.
Answer :
The sides of a square are
5x − 12y − 65 = 0 … (1)
5x − 12y + 26 = 0 … (2)
We observe that lines (1) and (2) are parallel. So, the distance between them will give the length of the side of the square.
Let d be the distance between the given lines.
⇒d=-65-2652+-122=9113=7
∴ Area of the square = 72
= 49 square units
Q3.
Answer :
The equation of given line is
x + 7y + 2 = 0 … (1)
The equation of a line parallel to line x + 7y + 2 = 0 is given below:
x+7y+λ=0 … (2)
The line x+7y+λ=0 is at a unit distance from the point (1, −1).
∴1=1-7+λ1+49⇒λ-6=±52⇒λ=6+52, 6-52
Required lines:
x+7y+6+52=0 and x+7y+6-52=0.
Q4.
Answer :
Let d1 be the distance between lines 2x + 3y = 19 and 2x + 3y = 6,
while d2 is the distance between lines 2x + 3y + 7 = 0 and 2x + 3y = 6
∴d1=-19–622+32 and d2=7–622+32⇒d1=-1313 =13 and d2=1313=13
Hence, the lines 2x + 3y = 19 and 2x + 3y + 7 = 0 are equidistant from the line 2x + 3y = 6
Q5.
Answer :
The given equations of the lines can be written as:
3x+2y-73=0 … (1)
3x + 2y + 6 = 0 … (2)
Let the equation of the line midway between the parallel lines (1) and (2) be
3x+2y+λ=0 … (3)
The distance between (1) and (3) and the distance between (2) and (3) are equal.
∴-73-λ32+22=6-λ32+22⇒-λ+73=6-λ⇒6-λ=λ+73⇒λ=116
Equation of the required line:
3x+2y+116=0⇒18x+12y+11=0
Page 23.102 Ex 23.17
Q1.
Answer :
The given lines are
a1x + b1y + c1 = 0 … (1)
a1x + b1y + d1 = 0 … (2)
a2x + b2y + c2 = 0 … (3)
a2x + b2y + d2 = 0 … (4)
The area of the parallelogram formed by the lines a1x + b1y + c1 = 0, a1x + b1y + d1 = 0, a2x + b2y + c2 = 0 and a2x + b2y + d2 = 0 is given below:
Area=c1-d1c2-d2a1a2b1b2
∵a1a2b1b2=a1b2-a2b1
∴Area=c1-d1c2-d2a1b2-a2b1=d1-c1d2-c2a1b2-a2b1
If the given parallelogram is a rhombus, then the distance between the pair of parallel lines are equal.
∴ c1-d1a12+b12=c2-d2a22+b22
Q2.
Answer :
The given lines are
3x − 4y + a = 0 … (1)
3x − 4y + 3a = 0 … (2)
4x − 3y − a = 0 … (3)
4x − 3y − 2a = 0 … (4)
Area of the parallelogram=c1-d1c2-d2a1b2-a2b1⇒Area of the parallelogram=a-3a2a-a-9+16=2a27square units
Q3.
Answer :
The given lines are
lx + my + n = 0 … (1)
mx + ly + n’ = 0 … (2)
lx + my + n’ = 0 … (3)
mx + ly + n = 0 … (4)
Solving (1) and (2), we get,
B≡mn’-lnl2-m2, mn-ln’l2-m2
Solving (2) and (3), we get,
C≡-n’m+l, -n’m+l
Solving (3) and (4), we get,
D≡mn-ln’l2-m2, mn’-lnl2-m2
Solving (1) and (4), we get,
A≡-nm+l, -nm+l
Let m1 and m2 be the slope of AC and BD.
m1=-n’m+l+nm+l-n’m+l+nm+l=1
and m2=mn’-lnl2-m2-mn-ln’l2-m2mn-ln’l2-m2-mn’-lnl2-m2 =mn’-ln-mn+ln’mn-ln’-mn’+ln =-1
∴m1m2=-1
Hence, diagonals of the parallelogram intersect at an angle π2.
Page 23.108 Ex 23.18
Q1.
Answer :
We know that, the equations of two lines passing through a point x1,y1 and making an angle α with the given line y = mx + c are
y-y1=m±tanα1∓mtanαx-x1
Here,
x1=0, y1=0, α=45∘ and m=-3
So, the equations of the required lines are
y-0=-3+tan45∘1+3tan45∘x-0 and y-0=-3-tan45∘1-3tan45∘x-0⇒y=-3+11+3x and y=3+13-1x⇒y=-3+1-233-1x and y=3+1+233-1x⇒y=3-2x and y=3+2x
Q2.
Answer :
We know that the equations of two lines passing through a point x1,y1 and making an angle α with the given line y = mx + c are
y-y1=m±tanα1∓mtanαx-x1
Here,
Equation of the given line is,x+y+3y-x=a⇒3+1y=3-1x+a⇒y=3-13+1x+a3+1Comparing this equation with y=mx+cwe get,m=3-13+1
∴ x1=0, y1=0, α=75∘, m=3-13+1=2-3
and tan75∘=2+3
So, the equations of the required lines are
y-0=2-3+tan75∘1-2-3tan75∘x-0 and y-0=2-3-tan75∘1+2-3tan75∘x-0⇒y=2-3+2+31-2-32+3x and y=2-3-2-31+2-32+3x⇒y=41-1x and y=-3x⇒x=0 and 3x+y=0
Q3.
Answer :
We know that the equations of two lines passing through a point x1,y1 and making an angle α with the given line y = mx + c are
y-y1=m±tanα1∓mtanαx-x1
Here,
Equation of the given line is,6x+5y-8=0⇒5y=-6x+8⇒y=-65x+85Comparing this equation with y=mx+cwe get,m=-65
x1=2, y1=-1, α=45∘, m=-65
So, the equations of the required lines are
y+1=-65+tan45∘1+65tan45∘x-2 and y+1=-65-tan45∘1-65tan45∘x-2⇒y+1=-65+11+65x-2 and y+1=-65-11-65x-2⇒y+1=-111x-2 and y+1=-11-1x-2⇒x+11y+9=0 and 11x-y-23=0
Q4.
Answer :
We know that the equations of two lines passing through a point x1,y1 and making an angle α with the given line y = m’x + c are
y-y1=m’±tanα1∓m’tanαx-x1
Here,
x1=h, y1=k, α=tan-1m, m’=m.
So, the equations of the required lines are
y-k=m+m1-m2x-h and y-k=m-m1+m2x-h⇒y-k=2m1-m2x-h and y-k=0⇒y-k1-m2=2mx-h and y=k
Q5.
Answer :
We know that the equations of two lines passing through a point x1,y1 and making an angle α with the given line y = mx + c are
y-y1=m±tanα1∓mtanαx-x1
Here,
Equation of the given line is,3x+y=1⇒y=-3x+1Comparing this equation with y=mx+cwe get,m=-3
x1=3, y1=-2, α=60∘, m=-3
So, the equations of the required lines are
y+2=-3+tan60∘1+3tan60∘x-3 and y+2=-3-tan60∘1-3tan60∘x-3⇒y+2=-3+31+3x-3 and y+2=-3-31-3x-3⇒y+2=0 and y+2=3x-3⇒y+2=0 and 3x-y=2+33
Q6.
Answer :
We know that the equations of two lines passing through a point x1,y1 and making an angle α with the given line y = mx + c are
y-y1=m±tanα1∓mtanαx-x1
Here,
Equation of the given line is,3x+y-5=0⇒y=-3x+5Comparing this equation with y=mx+cwe get,m=-3
x1=2, y1=3, α=45∘, m=-3.
So, the equations of the required lines are
y-3=-3+tan45∘1+3tan45∘x-2 and y-3=-3-tan45∘1-3tan45∘x-2⇒y-3=-3+11+3x-2 and y-3=-3-11-3x-2⇒y-3=-12x-2 and y-3=2x-2⇒x+2y-8=0 and 2x-y-1=0
Page 23.109 Ex 23.18
Q7.
Answer :
Here , we are given △ABC is an isosceles right angled triangle .∠A+∠B+ ∠C=180°⇒90°+∠B+∠B=180°⇒∠B=45°, ∠C=45°
Now, we have to find the equations of the sides AB and AC, where 3x + 4y = 4 is the equation of the hypotenuse BC.
We know that the equations of two lines passing through a point x1,y1 and making an angle α with the given line y = mx + c are
y-y1=m±tanα1∓mtanαx-x1
Here,
Equation of the given line is,3x+4y=4⇒4y=-3x+4⇒y=-34x+1Comparing this equation with y=mx+cwe get,m=-34
x1=2, y1=2, α=45∘, m=-34
So, the equations of the required lines are
y-2=-34+tan45∘1+34tan45∘x-2 and y-2=-34-tan45∘1-34tan45∘x-2⇒y-2=-34+11+34x-2 and y-2=-34-11-34x-2⇒y-2=17x-2 and y-2=-71x-2⇒x-7y+12=0 and 7x+y-16=0
Q8.
Answer :
Let A (1, 2) be the vertex of square ABCD and BD be the diagonal that is along the line 8x − 15y = 0
Equation of the given line is,8x-15y=0⇒-15y=-8x⇒y=815xComparing this equation with y=mx+cwe get,m=815
So, the slope of BD will be 815.
Here, we have to find the equations of sides AB and AD.
We know that the equations of two lines passing through a point x1,y1 and making an angle α with the line whose slope is m.
y-y1=m±tanα1∓mtanαx-x1
Here,
m=815×1=1 y1=2 α=45∘
So, the equations of the required sides are
y-2=815+tan45∘1-815tan45∘x-1 and y-2=815-tan45∘1+815tan45∘x-1⇒y-2=815+11-815x-1 and y-2=815-11+815x-1⇒23x-7y-9=0 and 7x+23y-53=0
Q9.
Answer :
Let A2+3,5 be the vertex of the equilateral triangle ABC and x − y = 0 be the equation of BC.
Here, we have to find the equations of sides AB and AC, each of which makes an angle of 60∘ with the line x − y = 0
We know the equations of two lines passing through a point x1,y1 and making an angle α with the line whose slope is m.
y-y1=m±tanα1∓mtanαx-x1
Here,
x1=2+3, y1=5, α=60∘, m=1
So, the equations of the required sides are
y-5=1+tan60∘1-tan60∘x-2-3 and y-5=1-tan60∘1+tan60∘x-2-3⇒y-5=-2+3x-2-3 and y-5=-2-3x-2-3⇒y-5=-2+3x+2+32 and y-5=-2-3x+2-32+3⇒2+3x+y=2+43 and 2-3x+y-6=0
Hence, the second side is y+(2-3) x=6 and the equation of the third side is 2+3x+y=12+43
Q10.
Answer :
Let A (1, 2) be the vertex of square ABCD and BD be one diagonal, whose equation is 4x + 7y = 12
Here, we have to find the equations of sides AB and AD, each of which makes an angle of 45∘ with line 4x + 7y = 12
We know the equations of two lines passing through a point x1,y1 and making an angle α with the line whose slope is m.
y-y1=m±tanα1∓mtanαx-x1
Here,
Equation of the given line is4x+7y=9⇒y=-47x+94
∴ x1=1, y1=2, α=45∘, m=-47
So, the equations of the required sides are
y-2=-47+tan45∘1+47tan45∘x-1 and y-2=-47-tan45∘1-47tan45∘x-1⇒y-2=-47+11+47x-1 and y-2=-47-11-47x-1⇒y-2=311x-1 and y-2=-113x-1⇒3x-11y+19=0 and 11x+3y-17=0
Q11.
Answer :
Let A(1, 2) be the vertex of the triangle ABC and x + y = 0 be the equation of BC.
Here, we have to find the equations of sides AB and AC, each of which makes an angle of 60∘ with the line x + y = 0.
We know the equations of two lines passing through a point x1,y1 and making an angle α with the line whose slope is m.
y-y1=m±tanα1∓mtanαx-x1
Here,
x1=1, y1=2, α=60∘, m=-1
So, the equations of the required sides are
y-2=-1+tan60∘1+tan60∘x-1 and y-2=-1-tan60∘1-tan60∘x-1⇒y-2=3-13+1x-1 and y-2=3+13-1x-1⇒y-2=2-3x-1 and y-2=2+3x-1
Solving x + y = 0 and y-2=2-3x-1, we get:
x=-3+12, y=3+12
∴B≡-3+12, 3+12 or C≡3-12, -3-12
AB = BC = AD = =6 units
∴ Area of the required triangle = 3×624=332 square units
Q12.
Answer :
Let ABC be the isosceles triangle, where 7x − y + 3 = 0 and x + y − 3 = 0 represent the sides AB and AC, respectively.
Let AB = BC
∵ AB = BC
∴ tan B = tan C
Here,
Slope of AB = 7
Slope of AC = −1
Let m be the slope of BC.
Then, m-71+7m=m+11-m=m+1m-1⇒m-71+7m=±m+1m-1
Taking the positive sign, we get:
m2-8m+7=7m2+8m+1⇒m+3m-13=0⇒m=-3, 13
Now, taking the negative sign, we get:
m-7m-1=-7m+1m+1⇒m2-8m+7=-7m2-8m-1⇒m2=-1 (not possible)
Equations of the third side is
y+10=-3x-1 and y+10=13x-1⇒3x+y+7=0 and x-3y-31=0
Q13.
Answer :
We observe that (0,−4) lies on the line 2x + 3y + 12 = 0
If (3, −5) lies between the lines 2x + 3y − 7 = 0 and 2x + 3y + 12 = 0, then we have,
ax1+by1+c1ax2+by2+c1>0
Here, x1=0, y1=-4, x2=3, y2=-5, a=2, b=3 and c1=-7
Now,
ax1+by1+c1ax2+by2+c1=2×0-3×4-72×3-3×5-7ax1+by1+c1ax2+by2+c2=-19×-16>0
Thus, point (3,−5) lies between the given parallel lines.
The equation of the lines passing through (3,−5) and making an angle of 45° with the given parallel lines is given below:
y-y1=m±tanα1∓mtanαx-x1
Here, x1=3, y1=-5, α=45∘and m=-23
∴y+5=-23±tan45∘1∓-23tan45∘x-3⇒y+5=-23+11+23x-3 and y+5=-23-11-23x-3⇒y+5=15x-3 and y+5=-5x-3⇒x-5y-28=0 and 5x+y-10=0
Q14.
Answer :
Let A (2, −1) be the vertex of the equilateral triangle ABC and x + y = 2 be the equation of BC.
Here, we have to find the equations of the sides AB and AC, each of which makes an angle of 60∘ with the line x + y = 2
The equations of two lines passing through point x1,y1 and making an angle α with the line whose slope is m is given below:
y-y1=m±tanα1∓mtanαx-x1
Here,
x1=2, y1=-1, α=60∘, m=-1
So, the equations of the required sides are
y+1=-1+tan60∘1+tan60∘x-2 and y+1=-1-tan60∘1-tan60∘x-2⇒y+1=-1+31+3x-2 and y+1=-1-31-3x-2⇒y+1=2-3x-2 and y+1=2+3x-2
Solving x + y = 2 and y+1=2-3x-2, we get:
x=15+36, y=-3+36
∴B≡15+36, -3+36 or C≡15-36, -3-36
∴ AB = BC = AD = =23
Equations of its sides are given below: 2-3x-y-5+23=0 , 2+3x-y-5-23=0
Page 23.115 Ex 23.19
Q1.
Answer :
The given family of lines can be written as
x + 2y + 5 + λ (x − y) = 0
This line is of the form L1 + λL2 = 0, which passes through the intersection of L1 = 0 and L2 = 0.
⇒ x + 2y + 5 = 0
⇒ x − y = 0
Now, solving the lines:
-53,-53
This is a fixed point.
Q2.
Answer :
The equation of the straight line passing through the point of intersection of 2x + y − 1 = 0 and x + 3y − 2 = 0 is given below:
2x + y − 1 + λ (x + 3y − 2) = 0
⇒(2 + λ)x + (1 + 3λ)y − 1 − 2λ = 0
⇒x1+2λ2+λ+y1+2λ1+3λ=1
So, the points of intersection of this line with the coordinate axes are 1+2λ2+λ,0 and 0,1+2λ1+3λ.
It is given that the required line makes an area of 38 square units with the coordinate axes.
121+2λ2+λ×1+2λ1+3λ=38⇒33λ2+7λ+2=44λ2+4λ+1⇒9λ2+21λ+6=16λ2+16λ+4⇒7λ2-5λ-2=0⇒λ=1, -27
Hence, the equations of the required lines are
3x+4y-1-2=0 and 2-27x+1-67y-1+47=0⇒3x+4y-3=0 and 12x+y-3=0
Q3.
Answer :
The equation of the straight line passing through the points of intersection of 4x − 3y = 0 and 2x − 5y + 3 = 0 is given below:
4x − 3y + λ (2x − 5y + 3) = 0
⇒(4 + 2λ)x + (−3 − 5λ)y + 3λ = 0
⇒y=4+2λ3+5λx+3λ3+5λ
The required line is parallel to 4x + 5y + 6 = 0 or, y=-45x-65
∴4+2λ3+5λ=-45⇒λ=-1615
Hence, the required equation is
4-3215x-3-8015y-4815=0⇒28x+35y-48=0
Q4.
Answer :
The equation of the straight line passing through the points of intersection of x + 2y + 3 = 0 and 3x + 4y + 7 = 0 is
x + 2y + 3 + λ(3x + 4y + 7) = 0
⇒(1 + 3λ)x + (2 + 4λ)y + 3 + 7λ = 0
⇒y=-1+3λ2+4λx-3+7λ2+4λ
The required line is perpendicular to x − y + 9 = 0 or, y = x + 9
∴-1+3λ2+4λ×1=-1⇒λ=-1
Required equation is given below:
(1 − 3)x + (2 − 4)y + 3 − 7 = 0
⇒ x + y + 2 = 0
Q5.
Answer :
The equation of the straight line passing through the points of intersection of 2x − 7y + 11 = 0 and x + 3y − 8 = 0 is given below:
2x − 7y + 11 + λ(x + 3y − 8) = 0
⇒(2 + λ)x + (−7 + 3λ)y + 11 − 8λ = 0
(i) The required line is parallel to the x-axis. So, the coefficient of x should be zero.
∴2+λ=0⇒λ=-2
Hence, the equation of the required line is
0 + (−7 − 6)y + 11 + 16 = 0
⇒ 13y − 27 = 0
(ii) The required line is parallel to the y-axis. So, the coefficient of y should be zero.
∴-7+3λ=0⇒λ=73
Hence, the equation of the required line is
2+73x+0+11-8×73=0⇒13x-23=0
Q6.
Answer :
The equation of the straight line passing through the points of intersection of 2x + 3y + 1 = 0 and 3x − 5y − 5 = 0 is
2x + 3y + 1 + λ(3x − 5y − 5) = 0
⇒(2 + 3λ)x + (3 − 5λ)y + 1 − 5λ = 0
⇒ y=-2+3λ3-5λ-1-5λ3-5λ
The required line is equally inclined to the axes. So, the slope of the required line is either 1 or −1.
∴-2+3λ3-5λ=1 and -2+3λ3-5λ= -1⇒-2-3λ=3-5λ and 2+3λ=3-5λ⇒λ=52 and 18
Substituting the values of λ in (2 + 3λ)x + (3 − 5λ)y + 1 − 5λ = 0, we get the equations of the required lines.
2+152x+3-252y+1-252=0 and 2+38x+3-58y+1-58=0⇒19x-19y-23=0 and 19x+19y+3=0
Q7.
Answer :
The equation of the straight line passing through the point of intersection of x + y = 4 and 2x − 3y = 1 is
x + y − 4 + λ(2x − 3y − 1) = 0
⇒(1 + 2λ)x + (1 − 3λ)y − 4 − λ = 0 … (1)
⇒y=-1+2λ1-3λx+4+λ1-3λ
The equation of the line with intercepts 5 and 6 on the axis is
x5+y6=1 … (2)
The slope of this line is -65.
The lines (1) and (2) are perpendicular.
∴-65×-1+2λ1-3λ=-1⇒λ=113
Substituting the values of λ in (1), we get the equation of the required line.
⇒1+223x+1-11y-4-113=0⇒25x-30y-23=0
Q8.
Answer :
The equation of the straight line passing through the point of intersection of 3x − y = 5 and x + 3y = 1 is
3x − y − 5 + λ(x + 3y − 1) = 0
⇒(3 + λ)x + (−1 + 3λ)y − 5 − λ = 0 … (1)
⇒y=-3+λ-1+λx+5+λ-1+λ
The slope of the line that makes equal and positive intercepts on the axis is −1.
From equation (1), we have:
-3+λ-1+3λ=-1⇒λ=2
Substituting the value of λ in (1), we get the equation of the required line.
⇒3+2x+-1+6y-5-2=0⇒5x+5y-7=0
Q9.
Answer :
The equation of the straight line passing through the point of intersection of x − 3y + 1 = 0 and 2x + 5y − 9 = 0 is given below:
x − 3y + 1 + λ(2x + 5y − 9) = 0
⇒(1 + 2λ)x + (−3 + 5λ)y + 1 − 9λ = 0 … (1)
The distance of this line from the origin is 5.
1-9λ1+2λ2+5λ-32=5⇒1+81λ2-18λ=145λ2-130λ+50⇒64λ2-112λ+49=0⇒8λ-72=0⇒λ=78
Substituting the value of λ in (1), we get the equation of the required line.
1+148x+-3+358y+1-638=0⇒22x+11y-55=0⇒2x+y-5=0
Q10.
Answer :
The given straight line (2 + k)x + (1 + k)y = 5 + 7k can be written in the following way:
2x + y − 5 + k (x + y − 7) = 0
This line is of the form L1 + kL2 = 0, which passes through the intersection of the lines
L1 = 0 and L2 = 0, i.e. 2x + y − 5 = 0 and x + y − 7 = 0.
Solving 2x + y − 5 = 0 and x + y − 7 = 0, we get (−2, 9), which is the fixed point.
Page 23.116 (Very Short Answers)
Q1.
Answer :
The lines passing through (a, b) and parallel to the x-axis and y-axis are y = b and x = a, respectively.
Therefore, their combined equation is given below:
(x – a)(y – b) = 0
Q2.
Answer :
The equation x2 − y2 = 0 represents a pair of straight line, which can be written in the following way:
(x + y)(x − y) = 0
So, the lines can be written separately in the following manner:
x + y = 0 … (1)
x − y = 0 … (2)
The third line is
x + 6y = 18 … (3)
Lines (1) and (2) are perpendicular to each other as their slopes are −1 and 1, respectively
⇒ −1 × 1 = −1
Therefore, the triangle formed by the lines (1), (2) and (3) is a right-angled triangle.
Thus, the orthocentre of the triangle formed by the given lines is the intersection of x + y = 0 and x − y = 0, which is (0, 0).
Q3.
Answer :
The centroid of a triangle with vertices x1,y1, x2,y2 and x3,y3 is given below:
x1+x2+x33, y1+y2+y33.
Therefore, the centre of the triangle having vertices (0, 0), (cos θ, sin θ) and (sin θ, − cos θ) is
0+cosθ+sinθ3,0+sinθ-cosθ3≡cosθ+sinθ3,sinθ-cosθ3
This point lies on the line y = 2x.
sinθ-cosθ3=2×cosθ+sinθ3⇒sinθ-cosθ=2cosθ+2sinθ⇒tanθ=-3
∴ tanθ = −3
Q4.
Answer :
Let A be the area of the triangle formed by the points O (0,0), A (acosθ,bsinθ) and B (acosθ,− bsinθ)
A=12001acosθbsinθ1acosθ-bsinθ1⇒A=12-absinθcosθ-absinθcosθ⇒A=absinθcosθ=12sin2θ
Now,
∴Amax=12, when sin2θ=1⇒∴Amax=12, when 2θ=π2⇒θ=π4
Hence, the area of the triangle formed by the given points is maximum when θ=π4.
Q5.
Answer :
The distance between the two parallel lines ax+by+c1=0 and ax+by+c2=0 is c1-c2a2+b2.
The given lines can be written as
4x + 3y − 11 = 0 … (1)
8x+6y-15=0 ⇒4x+3y-152=0 … (2)
Let d be the distance between the lines (1) and (2).
d=-11–15242+32=710 units
Q6.
Answer :
The equation xy = 0 represents a pair of straight lines.
The lines can be written separately in the following way:
x = 0 … (1)
y = 0 … (2)
The third line is
x + y = 1 … (3)
Lines (1) and (2) are perpendicular to each other as they are coordinate axes.
Therefore, the triangle formed by the lines (1), (2) and (3) is a right-angled triangle.
Thus, the orthocentre of the triangle formed by the given lines is the intersection of x = 0 and y = 0, which is (0, 0).
Q7.
Answer :
The given lines are
x + ay + a = 0 … (1)
bx + y + b = 0 … (2)
cx + cy + 1 = 0 … (3)
It is given that the lines (1), (2) and (3) are concurrent.
∴1aab1bcc1=0⇒1-bc-ab-bc+abc-c=0⇒1-bc-ab+abc+abc-ac=0⇒2abc-ab-bc-ca=-1
Hence, the value of 2abc − ab − bc − ca is −1
Q8.
Answer :
The point of intersection of the coordinate axes is (0, 0).
Let us find the intersection of the line (sec θ − tan θ) x + (sec θ + tan θ) y = 2 and the coordinate axis.
For x-axis:
y = 0, x=2secθ-tanθ
For y-axis:
x = 0, y=2secθ+tanθ
Thus, the coordinates of the triangle formed by the coordinate axis and the line (sec θ − tan θ) x + (sec θ + tan θ) y = 2 are (0, 0), 2secθ-tanθ,0 and 0,2secθ+tanθ.
Let A be the area of the required triangle.
∴ A=120012secθ-tanθ0102secθ+tanθ1⇒A=12×2secθ-tanθ×2secθ+tanθ⇒A=2secθ-tanθsecθ+tanθ=2sec2θ-tan2θ=2
Hence, the area of the triangle is 2 square units.
Q9.
Answer :
The given lines are
l1x + m1y + n1 = 0 … (1)
l2x + m2y + n2 = 0 … (2)
lsub>1x + msub>1y + nsub>1′ = 0 … (3)
l2x + m2y + n2‘ = 0 … (4)
Let (1), (2), (3) and (4) represent the sides AB, BC, CD and DA, respectively.
The equation of diagonal AC passing through the intersection of (2) and (3) is given by
lsub>1x + msub>1y + nsub>1’ +λ(l2x + m2y + n2) = 0
⇒l1+λl2x+m1+λm2y+n1’+λn2=0⇒Slope of diagonal AC=-l1+λl2m1+λm2
Also, the equation of diagonal BD, passing through the intersection of (1) and (2), is given by
l1x + m1y + n1 +μ(l2x + m2y + n2) = 0
⇒l1+μl2x+m1+μm2y+n1+μn2=0⇒Slope of diagonal BD=-l1+μl2m1+μm2
The diagonals are perpendicular to each other.
∴ l1+λl2m1+λm2l1+μl2m1+μm2=-1
⇒l1+λl2l1+μl2=-m1+λm2m1+μm2Let λ=-1, μ=1⇒l1-l2l1+l2=-m1-m2m1+m2⇒l12-l22=-m12-m22⇒l12-l22+m12-m22=0
Q10.
Answer :
Let the given point be A(3,8) and its image in the line x + 3y − 7 = 0 is B(h,k).
The midpoint of AB is 3+h2,8+k2 that lies on the line x + 3y − 7 = 0.
∴3+h2+3×8+k2-7=0
h+3k+13=0 … (1)
AB and the line x + 3y − 7 = 0 are perpendicular.
∴Slope of AB×Slope of the line=-1⇒k-8h-3×-13=-1
⇒3h-k-1=0 … (2)
Solving (1) and (2), we get:
(h, k) = (−1, −4)
Hence, the image of the point (3,8) in the line x + 3y − 7 = 0 is (−1,−4).
Q11.
Answer :
The given lines can be written as
mx – y + 1 = 0 … (1)
3x + 4y – 9 = 0 … (2)
Solving (1) and (2) by cross multiplication, we get:
x9-4=y3+9m=14m+3⇒x=54m+3, y=9m+34m+3
For x to be integer we have, 4m+3=1,-1,5 and -5⇒m=-12,-1,12 and -2
Hence, the integral values of m are -1 and -2.
Q12.
Answer :
The given lines are
(b − c)x + (c − a)y + (a − b) = 0 … (1)
(b3 − c3)x + (c3 − a3)y + (a3 − b3) = 0 … (2)
The lines (1) and (2) will represent the same lines if
b-cb3-c3=c-ac3-a3=a-ba3-b3⇒b-cb-cb2+bc+c2=c-ac-ac2+ac+a2=a-ba-ba2+ab+b2⇒1b2+bc+c2=1c2+ac+a2=1a2+ab+b2 ∵a≠b≠c
⇒b2+bc+c2=c2+ac+a2 and c2+ac+a2=a2+ab+b2⇒a-ba+b+c=0 and b-cb+c+a=0⇒a+b+c=0 ∵a≠b≠c
Hence, the given lines will represent the same lines if a + b + c = 0.
Q13.
Answer :
The point of intersection of the line ax + by + c = 0 with the coordinate axis are-ca,0 and 0,-cb.
So, the vertices of the triangle are (0, 0), -ca,0 and 0,-cb.
Let A be the area of the required triangle.
A=12001-ca010-cb1A=12-ca×-cb=12c2ab
It is given that a, b and c are in GP.
∴b2=ac
⇒A=12b4a2×ab=12ba3square units
Q14.
Answer :
The given lines can be written separately in the following way:
a x + b y + c = 0; x, y ≥ 0 … (1)
-a x + b y + c = 0; x < 0 y ≥ 0 … (2)
-a x – b y + c = 0; x < 0 y < 0 … (3)
a x – b y + c = 0; x ≥ 0 y < 0 … (4)
The lines and the region enclosed between them is shown below.
So, the area of the figures formed by the lines a |x| + b |y| + c = 0 is
4×12ca×cb=2c2ab square units
Q15.
Answer :
Let (h, k) be the locus.
It is given that the sum of distances of (h, k) from the coordinate axis is unity.
∴ |h| + |k| = 1
Taking locus of (h, k), we get:
|x| + |y| = 1
This represents a square.
Page 23.116 (Multiple Choice Questions)
Q1.
Answer :
(a) (1,1)
Let ax + by + c = 0 be the variable line. It is given that the algebraic sum of the distances
of the points (1, 1), (2, 0) and (0, 2) from the line is equal to zero.
∴a+b+ca2+b2+2a+0+ca2+b2+0+2b+ca2+b2=0⇒3a+3b+3c=0⇒a+b+c=0
Substituting c = – a – b in ax + by + c = 0, we get:
ax+by-a-b=0⇒ax-1+by-1=0⇒x-1+bay-1=0
This line is of the form L1+λL2=0, which passes through the intersection of L1=0 and L2=0, i.e. x – 1 = 0 and y – 1 = 0.
⇒ x = 1, y = 1
Q2.
Answer :
(c) cos-145
Let the coordinates of the right-angled isosceles triangle be O(0, 0), A(a, 0) and B(0, a).
Here, BD and AE are the medians drawn from the acute angles B and A, respectively.
∴ Slope of BD = m1
= 0-aa2-0
= -2
Slope of AE = m2
= a2-00-a
=-12
Let θ be the angle between BD and AE.
tan θ=-2+121+1 =34⇒cos θ=432+42⇒cos θ=45⇒θ=cos-145
Hence, the acute angle between the medians is cos-145.
Page 23.117 (Multiple Choice Questions)
Q3.
Answer :
(a) 0
Let A(1, 2), B(2, 1) and C3+32,3+32 be the given points.
∴AB=2-12+1-22 =2BC=3+32-22+3+32-12 =2AC=3+32-12+3+32-22 =2
Thus, ABC is an equilateral triangle.
We know that the orthocentre and the circumcentre of an equilateral triangle are same.
So, the distance between the the orthocentre and the circumcentre of the triangle
with vertices (1, 2), (2, 1) and 3+32,3+32 is 0.
Q4.
Answer :
(a) 9x − 20y + 96 = 0
Let the required line intersects the coordinate axis at (a, 0) and (0, b).
The point (−4, 3) divides the required line in the ratio 5 : 3
∴-4=5×0+3×a5+3 and 3=5×b+3×05+3⇒a=-323 and b=245
Hence, The equation of the required line is given below:
x-323+y245=1⇒-3×32+5y24=1⇒-9x+20y=96⇒9x-20y+96=0
Q5.
Answer :
(d) cannot be found
The point which divides the join of (1, 2) and (3, 4) externally in the ratio 1 :1 is 1×3-1×11-1,1×4-1×21-1
which is not defined .
Therefore,it is not possible to externally divide the line joining two points in the ratio 1:1
Q6.
Answer :
(d) 43
The equation of the line perpendicular to 3x + y = 3 is given below:
x – 3y + λ= 0
This line passes through (2, 2).
2 – 6 + λ = 0
⇒λ=4
So, the equation of the line will be
x – 3y + 4 = 0
⇒y=13x+43
Hence, the y-intercept is 43.
Q7.
Answer :
(c) A.P.
The given lines are
ax + 12y + 1 = 0 … (1)
bx + 13y + 1 = 0 … (2)
cx + 14y + 1 = 0 … (3)
It is given that (1), (2) and (3) are concurrent.
a121b131c141=0⇒a13-14-12b-c+14b-13c=0⇒-a-12b+12c+14b-13c=0⇒-a+2b-c=0⇒2b=a+c
Hence, a, b and c are in AP.
Q8.
Answer :
(a) 0
The given lines are
x − 2y + 3 = 0 … (1)
λx + 3y + 1 = 0 … (2)
4x − λy + 2 = 0 … (3)
It is given that (1), (2) and (3) are concurrent.
∴1-23λ314-λ2=0⇒6+λ+22λ-4+3-λ2-12=0⇒6+λ+4λ-8-3λ2-36=0⇒5λ-3λ2-38=0⇒3λ2-5λ+38=0
The discriminant of this equation is 25-4×3×38=-431
Hence, there is no real value of λ for which the lines x − 2y + 3 = 0, λx + 3y + 1 = 0 and 4x − λy + 2 = 0 are concurrent.
Q9.
Answer :
(b) x-3y = 4
The equation of the sides AB, BC and CA of ∆ABC are y − x = 2, x + 2y = 1 and 3x + y + 5 = 0, respectively.
Solving the equations of AB and BC, i.e. y − x = 2 and x + 2y = 1, we get:
x = − 1, y = 1
So, the coordinates of B are (−1, 1).
The altitude through B is perpendicular to AC.
∴ Slope of AC=-3
Thus, slope of the altitude through B is 13.
Equation of the required altitude is given below:
y-1=13x+1⇒x-3y+4=0
Q10.
Answer :
(a) 4p12 +p22 = a2
The given lines are
x sec θ + y cosec θ = a … (1)
x cos θ − y sin θ = a cos 2 θ … (2)
p1 and p2 are the perpendiculars from the origin upon the lines (1) and (2), respectively.
p1=-asec2θ++cosec2θ and p2=-acos2θcos2θ+sin2θ⇒p1=-asinθcosθsin2θ+cos2θ and p2=-acos2θ⇒p1=12-a×2sinθcosθ and p2=-acos2θ⇒p1=12-asin2θ and p2=-acos2θ⇒4p12+p22=a2sin22θ+cos22θ =a2
Q11.
Answer :
(d) none of these
The given points are (a+3)(a+4),a+3,(a+2)(a+3),(a+2) and (a+1)(a+2),(a+1).
Let A be the area of the triangle formed by these points.
Then, A=12x1y2-y3+x2y3-y1+x3y1-y2⇒A=12a+3a+4a+2-a-1+a+2a+3a+1-a-3+a+1a+2a+3-a-2⇒A=12a+3a+4-2a+2a+3+a+1a+2⇒A=12a2+7a+12-2a2-10a-12+a2+3a+2⇒A=1
Q12.
Answer :
(b) 23,2
Given:
a + b + c = 0
Substituting c = − a − b in 3ax + by + 2c = 0, we get:
3ax+by-2a-2b=0⇒a3x-2+by-2=0⇒3x-2+bay-2=0
This line is of the form L1+λL2=0, which passes through the intersection of the lines L1 and L2, i.e. 3x-2=0 and y-2=0.
Solving 3x-2=0 and y-2=0, we get:
x=23, y=2
Hence, the required fixed point is 23,2.
Q13.
Answer :
(c) 3 :1
Let the points (−3, −4) and (1, −2) be divided by y-axis at (0,t) in the ratio m:n.
∴ m-3nm+n,-2m-4nm+n=0,t
⇒ 0=m-3nm+n⇒m:n=3:1
Q14.
Answer :
(a) 17
Let A be the area of the triangle formed by the points (−4, −1), (1, 2) and (4, −3).
∴ A=12x1y2-y3+x2y3-y1+x3y1-y2⇒A=12-42+3+1-3+1+4-1-2⇒A=17
Q15.
Answer :
(d) 4:9
Let the line segment joining the points (1, 2) and (−2, 1) be divided by the line 3x + 4y = 7 in the ratio m:n.
Then, the coordinates of this point will be -2m+nm+n,m+2nm+n that lie on the line.
3x + 4y = 7
3×-2m+nm+n+4×m+2nm+n=7⇒-2m+11n=7m+7n⇒-9m=-4n⇒m:n=4:9
Page 23.118 (Multiple Choice Questions)
Q16.
Answer :
(b) 2x+5y = 20
Let the equation of the line be xa+yb=1
The coordinates of the intersection of this line with the coordinate axes are (a, 0) and (0, b).
The midpoint of (a, 0) and (0, b) is a2,b2
According to the question:
a2,b2=5,2⇒a2=5, b2=2⇒a=10, b=4
The equation of the required line is given below:
x10+y4=1⇒2x+5y=20
Q17.
Answer :
(a) 118
The area of a triangle with vertices D (x, 3x), B (−3, 5) and C (4, −2) is given below:
Area of ∆DBC = 12×5+2-3-2-3x+43x-5
⇒Area of ∆DBC = 14x-7 sq units
Similarly, the area of a triangle with vertices A (6, 3), B (−3, 5) and C (4, −2) is given below:
∆ABC = 1265+2-3-2-3+43-5
⇒∆ABC = 492sq units
Given:
∆DBC:∆ABC = 1:2
214x-749=12⇒8x-4=7⇒x=118
Q18.
Answer :
(c) 1p2=1a2+1b2
It is given that p is the length of the perpendicular from the origin on the line xa+yb=1
1ax+1by-1=0∴p=0+0-11a2+1b2Squaring both sides,⇒1p2=1a2+1b2
Q19.
Answer :
(a) 5x+3y-20=0
A line perpendicular to 3x − 5y + 7 = 0 is given by
5x+3y+λ=0
This line passes through (1, 5).
5+15+λ=0⇒λ=-20
Therefore, the equation of the required line is 5x+3y-20=0
Q20.
Answer :
(c) a rhombus
The given lines can be written separately in the following manner:
ax + by + c = 0 … (1)
ax + by − c = 0 … (2)
ax − by − c = 0 … (3)
ax − by − c = 0 … (4)
Graph of the given lines is given below:
Clearly, AB=BC=CD=DA=a2c2+b2c2=a2+b2c
Thus, the region formed by the given lines is ABCD, which is a rhombus.
Q21.
Answer :
Let (h, k) be the third vertex of the triangle.
It is given that the area of the triangle with vertices (h, k), (−2, −1) and (3, 2) is 4 square units.
12h-1-2-3-1-k-22-k=4
⇒3h-5k+1=±8
Taking positive sign, we get,
3h-5k+1=8
3h-5k-7=0 … (1)
Taking negative sign, we get,
3h-5k+9=0 … (2)
The vertex (h, k) lies on the line x + y = 5.
h+k-5=0 … (3)
On solving (1) and (3), we find (4, 1) to be the coordinates of the third vertex.
Similarly, on solving (2) and (3), we find (2, 3) to be the coordinates of the third vertex.
Q22.
Answer :
(d) 3π4
The midpoint of the line joining the points (4, −5) and (−2, 9) is (1, 2).
Let θ be the inclination of the straight line passing through the points (−3, 6) and (1, 2).
Then, tan θ=2-61+3=-1⇒θ=3π4
Q23.
Answer :
(c) 35334
The given lines can be written as
5x + 3y − 7 = 0 … (1)
5x+3y+143=0 … (2)
Let d be the distance between the lines 5x + 3y − 7 = 0 and 15x + 9y + 14 = 0
Then, d=-7-14352+32⇒d=35334
Q24.
Answer :
(a) 90°
Let m1 and m2 be the slope of the lines 2x − y + 3 = 0 and x + 2y + 3 = 0, respectively.
Let θ be the angle between them.
Here, m1 =2 and m2=-12
∵m1m2=-1
Therefore, the angle between the given lines is 90°.
Q25.
Answer :
(b) 1
It is given that the lines 3x + 4y = 5, 5x + 4y = 4 and λx + 4y = 6 meet at a point.
In other words, the given lines are concurrent.
34-554-4λ4-6=0⇒3-24+16-4-30+4λ-520-4λ=0⇒-24+120-16λ-100+20λ=0⇒4λ=4⇒λ=1
Q26.
Answer :
(b) (4,1)
Let A(−1, −6), B(2, −5) and C(7, 2) be the given vertex. Let D(h, k) be the fourth vertex.
The midpoints of AC and BD are 3,-2 and 2+h2,-5+k2 respectively.
We know that the diagonals of a parallelogram bisect each other.
∴3=2+h2 and -2=-5+k2⇒h=4 and k=1
Q27.
Answer :
(b) (4,7)
Let A(4, 8) and B(−2, 6) be the given vertex. Let C(h, k) be the third vertex.
The centroid of △ABC is 4-2+h3,8+6+k3.
It is given that the centroid of triangle ABC is (2, 7).
∴4-2+h3=2, 8+6+k3=7⇒h=4, k=7
Thus, the third vertex is (4, 7).
Q28.
Answer :
(c) 3
The lines x + q = 0, y − 2 = 0 and 3x + 2y + 5 = 0 are concurrent.
∴10q01-2325=0⇒15+4-0+q0-3=0⇒3q=9⇒q=3
Q29.
Answer :
(d) a=±2b
The midpoints of BC and AC are Da2,0 and Ea2,b2.
Slope of AD= 0-ba2-0
Slope of BE = -b2-a2
It is given that the medians are perpendicular to each other.
0-ba2-0×-b2-a2=-1⇒a=±2b
Q30.
Answer :
(b) 3x + 2y -2=0
Given:
4x + 3y − 7 = 0 … (1)
8x + 5y − 1 = 0 … (2)
The equation of the line with slope -32 is given below:
y=-32x+c
⇒32x+y-c=0 … (3)
The lines (1), (2) and (3) are concurrent.
∴43-785-1321-c=0⇒4-5c+1-3-8c+32-78-152=0⇒-20c+4+24c-92-56+1052=0⇒-40c+8+48c-9-112+1052=0⇒8c=8⇒c=1
On substituting c = 1 in y=-32x+c, we get:
y=-32x+1⇒3x+2y-2=0
Q31.
Answer :
(c) 2
Let A(0, 6), B(6, 0) and C(6, 6) be the vertices of the given triangle.
Centroid of △ABC=0+6+63,6+0+63 =4,4
Coordinates of N=6+62,6+02 =6,3Coordinates of P=0+62,6+62 =3,6Equation of MN is y=3Equation of MP is x=3As , we know that circumcentre of a triangle is the intersection of the perpendicular bisectors of any two sides .Therefore, coordinates of circumcentre is (3,3)
Thus, the coordinates of the circumcentre are (3, 3) and the centroid of the triangle is (4,4).
Let d be the distance between the circumcentre and the centroid.
∴ d=4-32+4-32=2
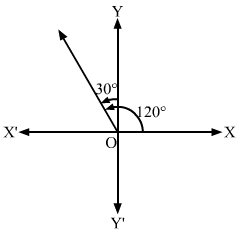
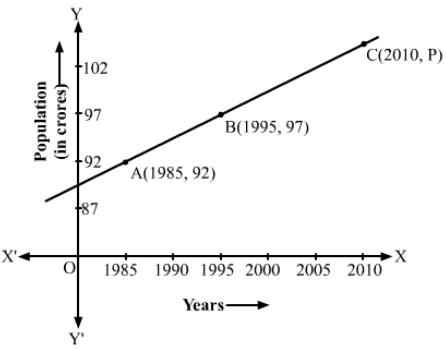

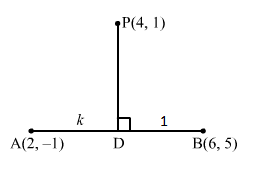
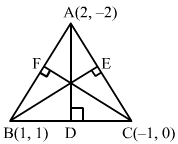
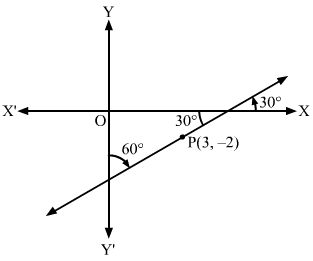
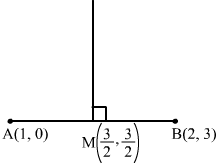
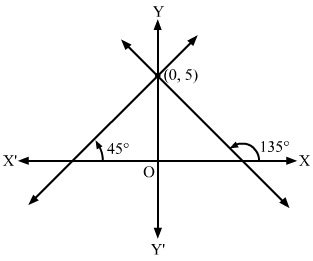
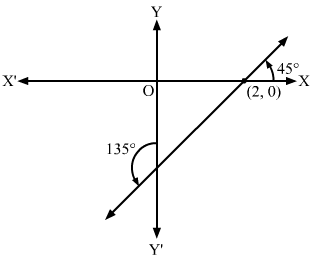
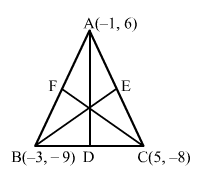
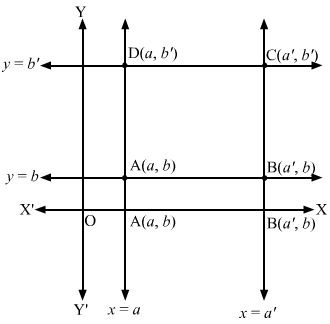
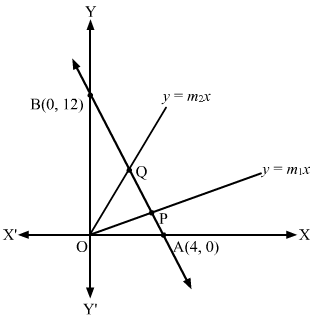
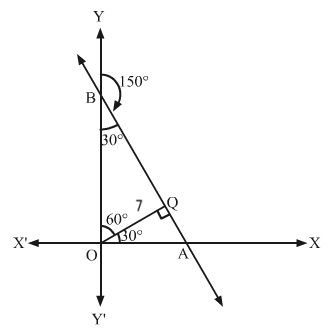
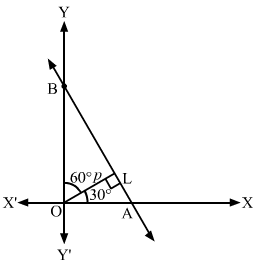
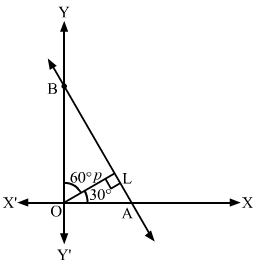
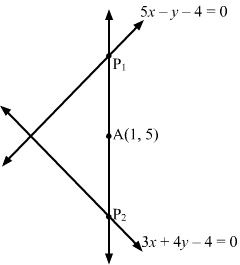
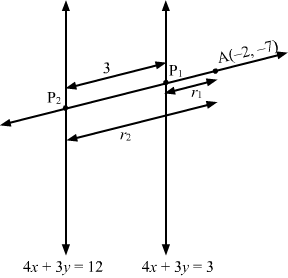
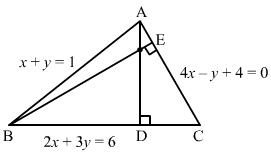
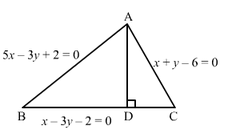
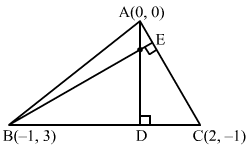
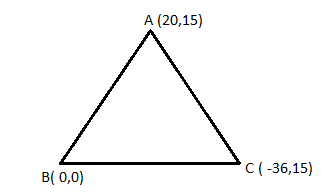
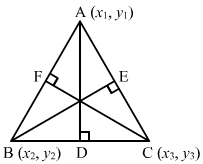
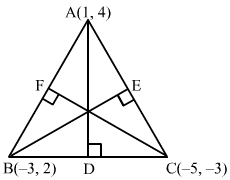
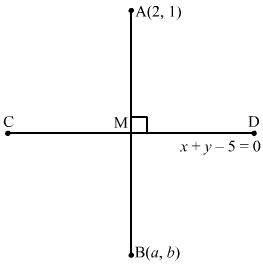
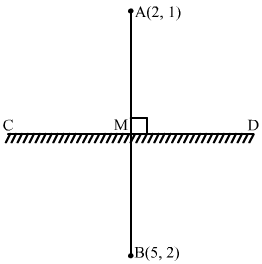
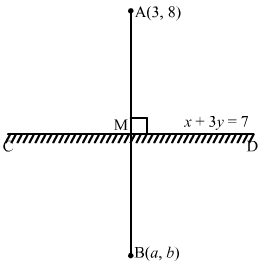
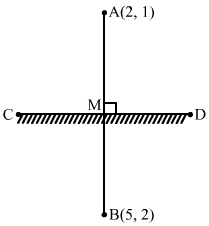
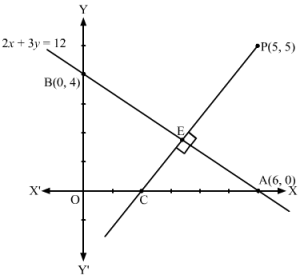
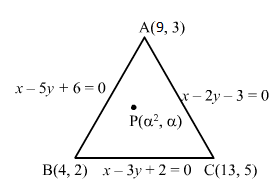
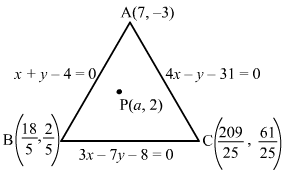
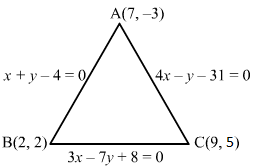
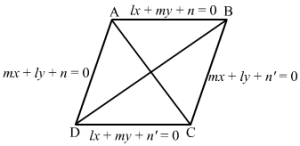
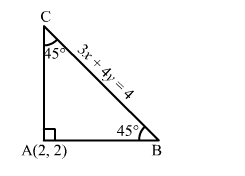
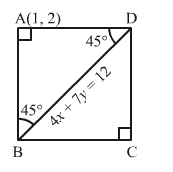
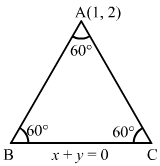
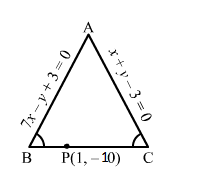
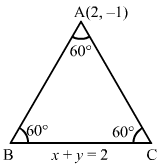
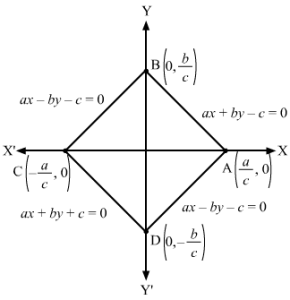

Leave a Reply