Notes For All Chapters Physics Class 11 CBSE
• Fluids are the sustances which can flow e.g., liquids and gases. It does not possess definite shape.
• When an object is submerged in a liquid at rest, the fluid exerts a force on its surface normally. It is called thrust of the liquid.
• Pressure
The thrust experienced per unit area of the surface of a liquid at rest is called pressure.
• When a liquid is in equilibrium, the force acting on its surface is perpendicular everywhere. The pressure is the same at the same horizontal level.
• The pressure at any point in the liquid depends on the depth (h) below the surface, density of liquid and acceleration due to gravity.
• Pascal’s Law
According to Pascal’s Law, the pressure applied to an enclosed liquid is transmitted undiminished to every portion of the liquid and the walls of the containing vessel.
• Hydraulic system works on Pascal’s law. Force exerted to area, ratio will be same at all cross¬sections.
Note: A large force is experienced in larger cross-section it a smaller force 4cross is applied in smaller by the relation section.
• A column of height h of a liquid of density p exerts a pressure P given
• If Pa be the atmospheric pressure then pressure in a liquid at a depth h from its free surface is given by P = Pa+ hρg. Relation is true for incompressible fluids only.
• The gauge pressure (Pg), is the difference of the absolute pressure (P) and the atmospheric pressure (Pa).
Absolute pressure (P) = Gauge pressure (Pg) + Atmospheric pressure (Pa)
Pg=P-Pa
• Archimedes Principle
When a body is partially or completely immersed in a liquid, it loses some of its weight. The loss
in weight of the body in the liquid is equal to the weight of the liquid displaced by the immersed
part of the body.
• The upward force excerted by the liquid displaced when a body is immersed is called buoyancy. Due to this, there is apparent loss in the weight experienced by the body.
• Law of Floatation
“A body floats in a liquid if weight of the liquid displaced by the immersed portion of the body is equal to the weight of the body.”
. When a body is immersed partially or wholly in a liquid, then the various forces acting on the body are
(i) upward thrust (T) acting at the centre of buoyancy and whose magnitude is equal to the
weight of the liquid displaced and
• (ii) the weight of the body (W) which acts vertically downward through its centre of gravity.
(a) When W > T, the body will sink in the liquid;
(b) When W = T, then the body will remain in equilibrium inside the liquid;
(c) When W < T, then the body will come upto the surface of the liquid in such a way that the weight of the liquid displaced due to its immersed portion equals the weight of the body. Thus the body will float with only a part of it immersed inside the liquid.
• The flow of a liquid is said to be steady or stream line flow if such particle of the fluid passing
through a given point travels along the same path and with same speed as the preceding particle passing through that very point.
• If the liquid flows over a horizontal surface in the form of layers of different velocities, then the flow of the liquid is called laminar flow.
• The flow of fluid in which velocity of all particles crossing a given point is not same and the motion of fluid becomes irregular or disordered is called turbulent flow.
• Equation of Continuity
According to equation of continuity, if there is no fluid source or sink along the length of a pipe, then mass of the fluid crossing any section of the pipe per unit time remains constant. i.e„ a1 v1ρ1 = a2v2 ρ2
For incompressible liquids (i.e., fluids) ρ1 = ρ2 and hence the equation is given as
a1v1=a2v2
– It means that speed of flow of liquid is more where the pipe is narrower and speed of flow is less
where the cross-section of pipe is more.
• Energy of a liquid
A liquid can possess three types of energies: (i) kinetic energy, (ii) potential energy and (iii) pressure energy
The energy possessed by a liquid due to its motion is called kinetic energy i.e., 1/2mv2.
The potential energy of a liquid of mass m at a height h is given by P.E. = mgh
The energy possessed by a liquid by virtue of its pressure is called pressure energy. Pressure energy of liquid in volume dV = PdV
Pressure energy per unit mass of the liquid
• Bernoulli’s Theorem
For an incompressible, non-viscous, irrotational liquid having streamlined flow, the sum of the pressure energy, kinetic energy and potential energy per unit mass is a constant i.e.,
• For steady flow of a non-viscous fluid along a horizontal pipe, Bernoulli’s equation is simplified as
• Viscosity
Viscosity is the property of the fluid (liquid or gas) by virtue of which an internal frictional force comes into play when the fluid is in motion in the form of layers having relative motion. It opposes the relative motion of the different layers. Viscosity is also called as fluid friction.
• The viscous force directly depends on the area of the layer and the velocity gradient.
• Coefficient of Viscosity
Coefficient of viscosity of a liquid is equal to the tangential force required to maintain a unit velocity gradient between two parallel layers of liquid each of area unity.
The SI unit of coefficient of viscosity is poiseuille (Pl) or Pa – s or Nm-2 s or kg m-1 s-1 . Dimensional formula of q is [ML-1T-1].
• Stoke’s Law
According to Stokes’ law the backward dragging force acting on a small spherical body of radius r moving with a velocity v through a viscous medius of coefficient of viscosity ή is given by
F = 6πήr
• Terminal Velocity
It is maximum constant velocity acquired by the body while falling freely in a viscous medium. This is attained when the apparent weight is compensated by the viscous force.
It is given by
where p be the density of the material of the body of radius r and o be the density of the medium.
• Poiseuille’s Equation
According to Poiseuille, if a pressure difference (P) is maintained across the two ends of a capillary tube of length ‘l’ and radius ‘r’, then the volume of liquid coming out of the tube per second is directly proportional to the pressure difference (P).
(ii) directly proportional to the fourth power of radius (r) of the capillary tube.
(iii) inversely proportional to the coefficient of viscosity (ή) of the liquid.
(iv) inversely proportional to the length (i) of the capillary tube.
It is given as
• Reynold’s Number
Reynold number Re is a dimensionless number whose value gives an approximate idea whether the flow of a fluid will be streamline or turbulent. It is given by
where p = density of fluid flowing with a speed u, d stands for the diameter of the pipe and q is the viscosity of the fluid. Value of Re remains same in any system of units.
• It is observed that flow is streamline or laminar for Re <= 1000 and the flow is turbulent for Re >= 2000. The flow becomes unsteady for Re between 1000 and 2000. The critical value of Re , at which turbulence sets, is same for the geometrically similar flows.
• Re may also be expressed as the ratio of inertial force (force due to inertia i.e., mass of moving fluid or due to inertia of obstacle in its path) to viscous force i.e.,
• Critical Velocity
The critical velocity is that velocity of liquid flow, upto which its flow is streamline and above which its flow becomes turbulent.
It is given by
where K is a dimensionless constant, q is coefficient of viscosity of liquid, p is density of liquid and r is the radius of tube.
• Surface Tension
It is the property of the liquid by virtue of which the free surface of liquid at rest tends to have minimum area and as such it behaves as a stretched elastic membrane.
• The force acting per unit length of line drawn on the liquid surface and normal to it parallel to the surface is called the force of surface tension.
It is given by
The SI unit of surface tension is Nm-1 and its dimensional formula is [MT-2],
• Surface Energy
Energy possessed by the surface of the liquid is called surface energy. Change in surface energy is the product of surface tension and change in surface area under constant temperature.
• The height to which water rises in a capillary tube of radius r is given by
where T is the surface tension of the liquid and 0 is the angle of contact.
Due to surface tension there is excess pressure on the concave side of a surface film of a liquid over
the convex side and is equal to 2T/r . For a soap bubble the excess pressure is 4T/r where, r denotes the radius of the surface.
• Angle of Contact
The angle which the tangent to the liquid surface at the point of contact makes with the solid surface inside the liquid is called angle of contact.
• Intermolecular force amongst molecules of the same material is called the force of cohesion. However, force amongst molecules of different materials is called the force of adhesion.
• Torricelli’s Theorem
According to this theorem, velocity of efflux i.e., the velocity with which the liquid flows out of on orifice {i.e., a narrow hole) is equal to that which a freely falling body would acquire in falling through a vertical distance equal to the depth of orifice below the free surface of liquid.
The velocity is given by
V = √2gh
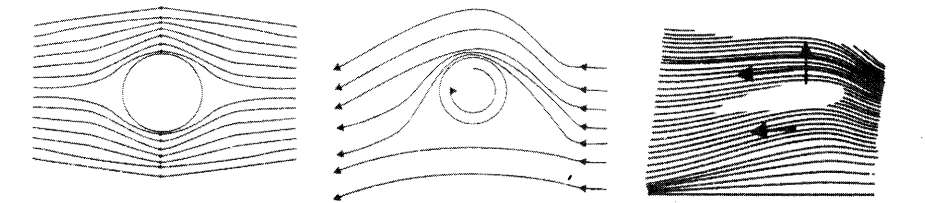
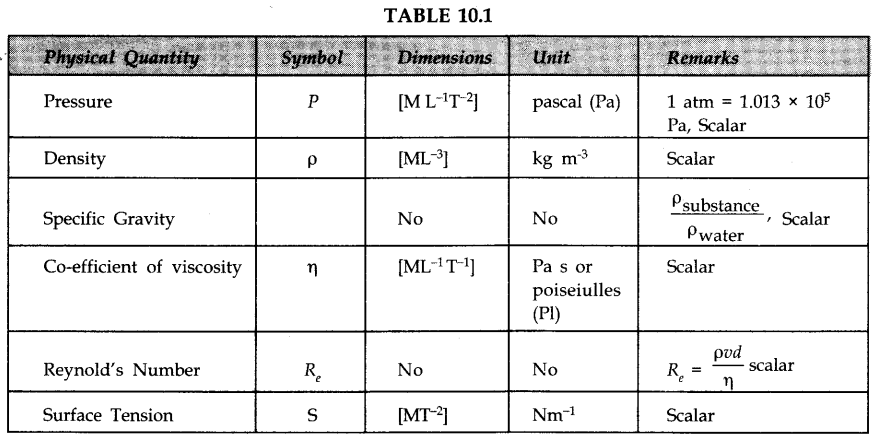
• Magnus Effect
When a ball is given a spin when it is in a streamline of air molecules, it will follow a curved path which is convex towards the greater pressure side. This idea is the basis of the ball from spin bowlers getting a lift and areodynamics.
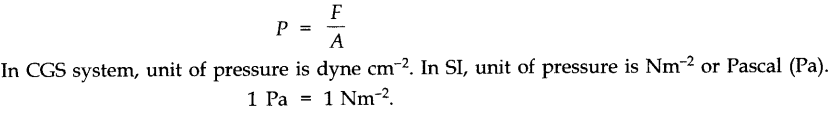
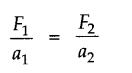
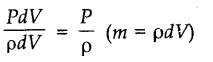
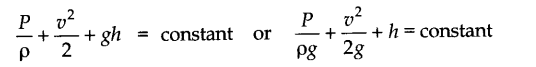
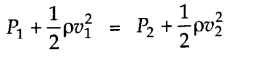
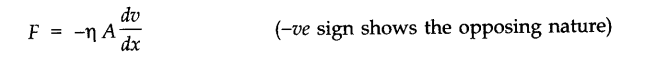
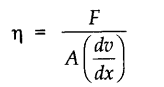
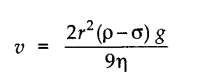
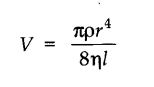
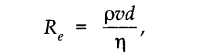
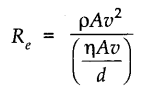
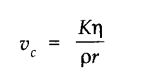
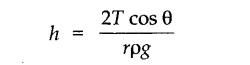



Leave a Reply