12.1
Estimate the fraction of molecular volume to the actual volume occupied by oxygen gas at STP. Take the diameter of an oxygen molecule to be 3 Å.
Solution :
Diameter of an oxygen molecule, d = 3Å
Radius, r = d/2 = 3/2 = 1.5 Å = 1.5 × 10–8 cm
Actual volume occupied by 1 mole of oxygen gas at STP = 22400 cm3
Molecular volume of oxygen gas, V = (4/3)πr3N
Where, N is Avogadro’s number = 6.023 × 1023 molecules/mole
∴ V = (4/3) × 3.14 × (1.5 × 10-8)3 × 6.023 × 1023 = 8.51 cm3
Ratio of the molecular volume to the actual volume of oxygen = 8.51 / 22400
= 3.8 × 10-4.
12.2
Molar volume is the volume occupied by 1 mol of any (ideal) gas at standard temperature and pressure (STP: 1 atmospheric pressure, 0 °C). Show that it is 22.4 litres.
Solution :
The ideal gas equation relating pressure (P), volume (V), and absolute temperature (T) is given as:
PV = nRT
Where,
R is the universal gas constant = 8.314 J mol–1 K–1
n = Number of moles = 1
T = Standard temperature = 273 K
P = Standard pressure = 1 atm = 1.013 × 105 Nm–2
∴ V = nRT / P
= 1 × 8.314 × 273 / (1.013 × 105)
= 0.0224 m3
= 22.4 litres
Hence, the molar volume of a gas at STP is 22.4 litres.
12.3
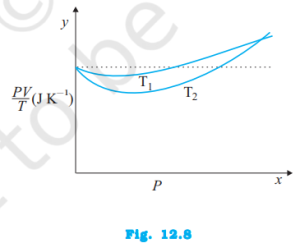
Figure 12.8 shows plot of PV/T versus P for 1.00×10–3 kg of oxygen gas at two different temperatures.
a. What does the dotted plot signify?
b. Which is true: T1 > T2 or T1 < T2?
c. What is the value of PV/T where the curves meet on the y-axis?
d. If we obtained similar plots for 1.00 ×10–3 kg of hydrogen, would we get the same value of PV/T at the point where the curves meet on the y-axis? If not, what mass of hydrogen yields the same value of PV/T (for low pressure high temperature region of the plot)? (Molecular mass of H2 = 2.02μ, of O2 = 32.0μ, R = 8.31 J mo1–1 K–1.)
Solution :
a. The dotted plot in the graph signifies the ideal behavior of the gas, i.e., the ratio PV/T is equal.
μR (μ is the number of moles and R is the universal gas constant) is a constant quality. It is not dependent on the pressure of the gas.
b. The dotted plot in the given graph represents an ideal gas. The curve of the gas at temperature T1 is closer to the dotted plot than the curve of the gas at temperature T2. A real gas approaches the behaviour of an ideal gas when its temperature increases. Therefore, T1 > T2 is true for the given plot.
c. The value of the ratio PV/T, where the two curves meet, is μR. This is because the ideal gas equation is given as:
PV = μRT
PV/T = μR
Where,
P is the pressure
T is the temperature
V is the volume
μ is the number of moles
R is the universal constant
Molecular mass of oxygen = 32.0 g
Mass of oxygen = 1 × 10–3 kg = 1 g
R = 8.314 J mole–1 K–1
∴ PV/T = (1/32) × 8.314
= 0.26 J K-1
Therefore, the value of the ratio PV/T, where the curves meet on the y-axis, is
0.26 J K–1.
d. If we obtain similar plots for 1.00 × 10–3 kg of hydrogen, then we will not get the same value of PV/T at the point where the curves meet the y-axis. This is because the molecular mass of hydrogen (2.02 u) is different from that of oxygen (32.0 u).
We have:
PV/T = 0.26 J K-1
R = 8.314 J mole–1 K–1
Molecular mass (M) of H2 = 2.02 u
PV/T = μR at constant temperature
Where, μ = m/M
m = Mass of H2
∴ m = (PV/T) × (M/R)
= 0.26 × 2.02 / 8.31
= 6.3 × 10–2 g = 6.3 × 10–5 kg
Hence, 6.3 × 10–5 kg of H2 will yield the same value of PV/T.
12.4
An oxygen cylinder of volume 30 litres has an initial gauge pressure of 15 atm and a temperature of 27 °C. After some oxygen is withdrawn from the cylinder, the gauge pressure drops to 11 atm and its temperature drops to 17 °C. Estimate the mass of oxygen taken out of the cylinder (R = 8.31 J mol–1 K–1, molecular mass of O2 = 32 μ).
Solution :
Volume of oxygen, V1 = 30 litres = 30 × 10–3 m3
Gauge pressure, P1 = 15 atm = 15 × 1.013 × 105 Pa
Temperature, T1 = 27°C = 300 K
Universal gas constant, R = 8.314 J mole–1 K–1
Let the initial number of moles of oxygen gas in the cylinder be n1.
The gas equation is given as:
P1V1 = n1RT1
∴ n1 = P1V1/ RT1
= (15.195 × 105 × 30 × 10-3) / (8.314 × 300) = 18.276
But n1 = m1 / M
Where,
m1 = Initial mass of oxygen
M = Molecular mass of oxygen = 32 g
∴m1 = n1M = 18.276 × 32 = 584.84 g
After some oxygen is withdrawn from the cylinder, the pressure and temperature reduces.
Volume, V2 = 30 litres = 30 × 10–3 m3
Gauge pressure, P2 = 11 atm = 11 × 1.013 × 105 Pa
Temperature, T2 = 17°C = 290 K
Let n2 be the number of moles of oxygen left in the cylinder.
The gas equation is given as:
P2V2 = n2RT2
∴ n2 = P2V2/ RT2
= (11.143 × 105 × 30 × 10-3) / (8.314 × 290) = 13.86
But n2 = m2 / M
Where,
m2 is the mass of oxygen remaining in the cylinder
∴ m2 = n2M = 13.86 × 32 = 453.1 g
The mass of oxygen taken out of the cylinder is given by the relation:
Initial mass of oxygen in the cylinder – Final mass of oxygen in the cylinder
= m1 – m2
= 584.84 g – 453.1 g
= 131.74 g
= 0.131 kg
Therefore, 0.131 kg of oxygen is taken out of the cylinder.
12.5
An air bubble of volume 1.0 cm3 rises from the bottom of a lake 40 m deep at a temperature of 12 °C. To what volume does it grow when it reaches the surface, which is at a temperature of 35 °C?
Solution :
Volume of the air bubble, V1 = 1.0 cm3 = 1.0 × 10–6 m3
Bubble rises to height, d = 40 m
Temperature at a depth of 40 m, T1 = 12°C = 285 K
Temperature at the surface of the lake, T2 = 35°C = 308 K
The pressure on the surface of the lake:
P2 = 1 atm = 1 ×1.013 × 105 Pa
The pressure at the depth of 40 m:
P1 = 1 atm + dρg
Where,
ρ is the density of water = 103 kg/m3
g is the acceleration due to gravity = 9.8 m/s2
∴ P1 = 1.013 × 105 + 40 × 103 × 9.8 = 493300 Pa
We have P1V1 / T1 = P2V2 / T2
Where, V2 is the volume of the air bubble when it reaches the surface
V2 = P1V1T2 / T1P2
= 493300 × 1 × 10-6 × 308 / (285 × 1.013 × 105)
= 5.263 × 10–6 m3 or 5.263 cm3
Therefore, when the air bubble reaches the surface, its volume becomes 5.263 cm3
12.6
Estimate the total number of air molecules (inclusive of oxygen, nitrogen, water vapour and other constituents) in a room of capacity 25.0 m3 at a temperature of 27 °C and 1 atm pressure.
Solution :
Volume of the room, V = 25.0 m3
Temperature of the room, T = 27°C = 300 K
Pressure in the room, P = 1 atm = 1 × 1.013 × 105 Pa
The ideal gas equation relating pressure (P), Volume (V), and absolute temperature (T) can be written as:
PV = kBNT
Where,
KB is Boltzmann constant = 1.38 × 10–23 m2 kg s–2 K–1
N is the number of air molecules in the room
∴ N = PV / kBT
= 1.013 × 105 × 25 / (1.38 × 10-23 × 300)
= 6.11 × 1026 molecules
Therefore, the total number of air molecules in the given room is 6.11 × 1026.
12.7
Estimate the average thermal energy of a helium atom at
1. room temperature (27 °C),
2. the temperature on the surface of the Sun (6000 K),
3. the temperature of 10 million Kelvin (the typical core temperature in the case of a star).
Solution :
1. At room temperature, T = 27°C = 300 K
Average thermal energy = (3/2)kT
Where k is Boltzmann constant = 1.38 × 10–23 m2 kg s–2 K–1
∴ (3/2)kT = (3/2) × 1.38 × 10-38 × 300
= 6.21 × 10–21J
Hence, the average thermal energy of a helium atom at room temperature (27°C) is 6.21 × 10–21 J.
2. On the surface of the sun, T = 6000 K
Average thermal energy = (3/2)kT
= (3/2) × 1.38 × 10-38 × 6000
= 1.241 × 10-19 J
Hence, the average thermal energy of a helium atom on the surface of the sun is 1.241 × 10–19 J.
3. At temperature, T = 107 K
Average thermal energy = (3/2)kT
= (3/2) × 1.38 × 10-23 × 107
= 2.07 × 10-16 J
Hence, the average thermal energy of a helium atom at the core of a star is 2.07 × 10–16 J.
12.8
Three vessels of equal capacity have gases at the same temperature and pressure. The first vessel contains neon (monatomic), the second contains chlorine (diatomic), and the third contains uranium hexafluoride (polyatomic). Do the vessels contain equal number of respective molecules? Is the root mean square speed of molecules the same in the three cases? If not, in which case is vrms the largest?
Solution :
All the three vessels have the same capacity, they have the same volume.
Hence, each gas has the same pressure, volume, and temperature.
According to Avogadro’s law, the three vessels will contain an equal number of the respective molecules. This number is equal to Avogadro’s number,
N = 6.023 × 1023.
The root mean square speed (vrms) of a gas of mass m, and temperature T, is given by the relation:
vrms = (3kT/m)1/2
where,
k is Boltzmann constant
For the given gases, k and T are constants.
Hence vrms depends only on the mass of the atoms, i.e.,
vrms ∝ (1/m)1/2
Therefore, the root mean square speed of the molecules in the three cases is not the same. Among neon, chlorine, and uranium hexafluoride, the mass of neon is the smallest. Hence, neon has the largest root mean square speed among the given gases.
12.9
At what temperature is the root mean square speed of an atom in an argon gas cylinder equal to the rms speed of a helium gas atom at – 20 °C? (atomic mass of Ar = 39.9 u, of He = 4.0 u).
Solution :
Temperature of the helium atom, THe = –20°C= 253 K
Atomic mass of argon, MAr = 39.9 u
Atomic mass of helium, MHe = 4.0 u
Let, (vrms)Ar be the rms speed of argon.
Let (vrms)He be the rms speed of helium.
The rms speed of argon is given by:
Therefore, the temperature of the argon atom is 2.52 × 103 K.
12.10
Estimate the mean free path and collision frequency of a nitrogen molecule in a cylinder containing nitrogen at 2.0 atm and temperature 17 °C. Take the radius of a nitrogen molecule to be roughly 1.0 Å. Compare the collision time with the time the molecule moves freely between two successive collisions (Molecular mass of N2 = 28.0 u).
Solution :
Mean free path = 1.11 × 10–7 m
Collision frequency = 4.58 × 109 s–1
Successive collision time ≈ 500 × (Collision time)
Pressure inside the cylinder containing nitrogen, P = 2.0 atm = 2.026 × 105 Pa
Temperature inside the cylinder, T = 17°C =290 K
Radius of a nitrogen molecule, r = 1.0 Å = 1 × 1010 m
Diameter, d = 2 × 1 × 1010 = 2 × 1010 m
Molecular mass of nitrogen, M = 28.0 g = 28 × 10–3 kg
The root mean square speed of nitrogen is given by the relation:
Collision frequency = vrms / l
= 508.26 / (1.11 × 10-7) = 4.58 × 109 s-1
Collision time is given as:
T = d / vrms
= 2 × 10-10 / 508.26 = 3.93 × 10-13 s
Time taken between successive collisions:
T ‘ = l / vrms
= 1.11 × 10-7 / 508.26 = 2.18 × 10-10 s
∴ T ‘ / T = 2.18 × 10-10 / (3.93 × 10-13) = 500
Hence, the time taken between successive collisions is 500 times the time taken for a collision.



Leave a Reply