Notes For All Chapters Science Class 6
On a day-to-day basis, we are faced with various instances when we are required to separate substances from one another. Whether it is picking out chillies from our paranthas/poha or separating tea leaves from tea while serving it, the need for separation of substances is something we encounter on a daily basis. It is usually because of one or all three of the following reasons:
1. To separate two dissimilar but useful elements like in the case of butter and milk. Milk is churned in order to obtain butter.
2. To segregate useless elements from the useful ones like in the case of separating tea leaves from tea.
3. To remove and discard impurities or potentially harmful substances like picking out small pieces of stones and other impurities from rice and wheat.
Figure 1 Separating tea leaves from tea
Problems arise when the materials to be separated are really small in size or differ in their composition. It is nearly impossible to separate grains of salt from grains of sand by hand or trying to separate oil from water. We might need to use methods other than simple handpicking even though for a lot of separation processes, even handpicking might be enough.
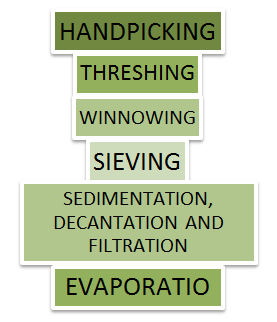
Methods of Separation
Handpicking: The simple process of separating slightly bigger sized harmful substances or other useful substances or impurities like small pieces of stones, husk and dirt from grains of wheat, pulses and rice is called handpicking. In situations when the quantity of such impurities is not very large, handpicking turns out to be a time-saving and convenient procedure of separating substances.
Figure 3 A group of individuals separating two types of grains
Threshing: After the crop is harvested, stalks are left to dry under the sun. A single stalk has some 100 pieces of grain seeds joined to it. It is manually impossible to pluck each grain seed which is very small in size from the stalk and hence handpicking as a method of separation does not work here. That is why we use a method called threshing to separate these grain seeds.
Thus, Threshing can be defined as the process of separating the edible part i.e. grain seeds from the stalk by either with the help of machines, bullocks or sometimes by beating them.
Figure 4 a) Threshing by hand b) Threshing by machine
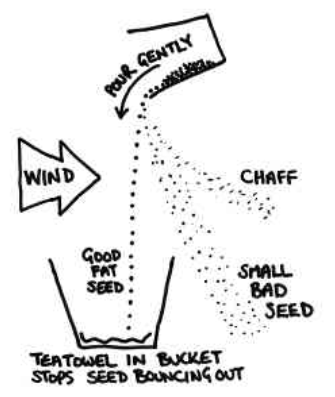
Winnowing: Even when threshing is done, husk or chaff is still attached to the grain seed and since the size of the two is quite similar, handpicking does not work and neither does threshing. Hence, a method called winnowing can be used.
Winnowing can be defined as the method of separating lighter husk particles and heavier grain seed components by blowing a current of air through them. The lighter husk particles are carried away by the wind and the grain seeds get separated. This husk can be further used as fodder for the cattle.
Figure 5 Process of winnowing
Sieving: Sometimes even after the grain seeds have passed through the stages of threshing and winnowing, husk may still be attached to the grain or it may have collected stones and dirt in the earlier stages which need to be removed and this separation is usually done with the help of a sieve.
Sieving is a very simple, convenient and time-saving process through which particles of varying sizes can be separated from each other with the help of a sieve. A sieve is nothing but a simple device with small pores in it which allow finer materials like flour to pass through leaving behind any impurities it might contain.
Figure 6 Sieving
Sedimentation, Decantation and Filtration
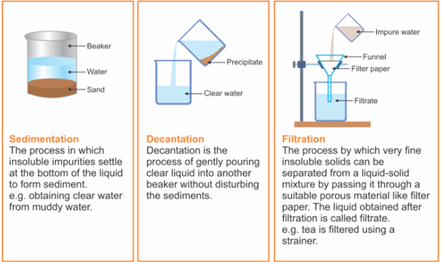
1. Sedimentation: Sedimentation can be defined as the process through which dirt and other heavier particles in a mixture settle at the bottom of the vessel when water is added to it. When the dust and dirt particles have settled, the clear water which forms the upper layer is moved to a different container and the dirt and dust is done away with. This technique can also be used to separate two liquids which do not mix with each other (also called immiscible liquids) and is called decantation.
2. Decantation: Decantation can be defined as a technique through which immiscible liquids or a liquid and a solid substance are separated. For example, take the case of oil and water. These are two examples of immiscible liquids. Once we pour oil in water, oil forms the upper layer of water and can be easily separated by gently pouring the mixture in another container till all the oil has been removed. Sometimes smaller dirt particles get carried along with the water in the process of decantation which needs to be further removed. This can be achieved through the process of filtration.
3. Filtration: Filtration is the process through which smaller particles like dirt etc. are separated from a solution by making the solution pass through a medium (often a filter paper). This medium is such that only liquids are able to pass through it because of the presence of very tiny pores in it. The filter paper is molded to form a cone and this cone-like structure is then affixed to a funnel through which the dirty solution is allowed to pass. Sometimes, filtration can also be applied to separate pulp and seeds from the juice. It can also be used to separate cottage cheese or paneer from milk.
Figure 7 Sedimentation, Decantation and Filtration
4. Evaporation: Evaporation is the process of converting liquid into gas or vapour by increasing the temperature or pressure of the liquid. This process is often used to separate salt from salt water or salty sea water. Sea water has a number of salts present in it. Shallow pits called evaporation ponds are constructed and salt water is allowed to stand in these. After some time, the water gets evaporated, leaving behind the salts. Common salt is separated from this mixture upon further purification.
Figure 8 Salt Evaporation Ponds
Use of more than one method of separation
Often, we are faced with mixtures and solutions that cannot be separated by use of a single separation technique. A number of such techniques need to be applied simultaneously to achieve the desired result.
Take for example the case of a salt and sand mixture. We know handpicking will not work and considering both of them weigh just about the same, neither will winnowing.
And hence we try to separate the two with the help of filtration or decantation.
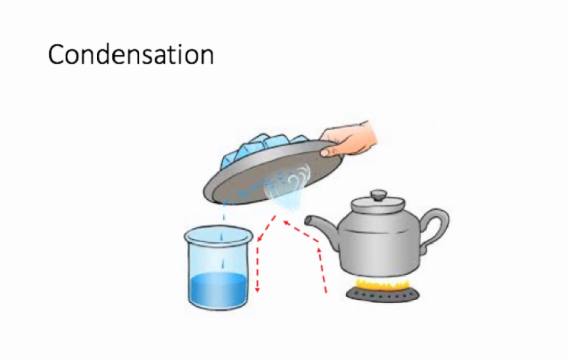
We take a beaker and add water to the said mixture of salt and sand. While the salt dissolves in water, the sand deposits at the bottom of the beaker and can be separated from the salt solution with the help of a filter paper or by gently pouring the salt solution in another container. We now have to separate the salt from water, for which we will simultaneously use the methods of evaporation and condensation. While heating the solution in a kettle, we observe that vapour or steam starts to rise from the spout of the kettle. What we then do is allow this steam to come in contact with a metal plate which has some ice on it. When this happens, the steam gets converted to small drops of water which we transfer to another container and thus successfully manage to separate salt which gets left behind in the kettle and the water which we collect in a separate container.
Condensation is the defined as the simple process of converting gas or vapour to its liquid form by decreasing the temperature or pressure exerted on it. This is what we did when we allowed the steam to come in contact with the cold metal plate
Figure 9 Use of more than one method of separation
Can Water Dissolve Any Amount of a Substance?
Even though water can dissolve a number of substances and solutions in it, it has a limit to how much it can dissolve. After a certain point, it stops dissolving any more of that substance and the substance collects at the bottom of the vessel. We say that the solution has become saturated.
A saturated solution is one that contains the maximum possible concentration of a particular solute. For example, if we continue to add increasing amounts of salt to a small quantity of water, there will come a point that the salt will not get mixed with the water and instead deposit at the bottom. At this point, we say that the solution has become saturated i.e. it is now incapable of dissolving any more of the given solute which is in this case, salt.
A salute is defined as a very small element in a solution that is dissolved in a solution.
One way of ensuring that the given amount of water takes more salt even after it has reached its saturation point is by heating the said water. This is because heating the solution helps to increase the solubility of salt or any solute and hence more amount of the same solute can now be dissolved in the same amount of water.
Some Important Definitions
Churning: The process of shaking milk or cream in order to allow lighter particles to come to the surface in order to make butter is called churning.
Pure Substance: This can be defined as a substance composed of only a single type of particle.
Impure Substance: A substance composed of more than one type of particles.
Sublimation: When a solid directly gets converted into vapour, this process is known as sublimation.
Magnetic Separation: This is another method of separation which allows metals (and other articles which are attracted to a magnet) to be separated from a mixture with the help of a magnetic or by applying a magnetic force to it. For example, a mixture of salt and iron filings can be separated with the help of a magnet.






Leave a Reply