Notes For All Chapters Maths Class 6
Number
A number is a mathematical object used to count, measure, and also label.
Comparing Numbers
1. Compare 4978 and 5643…….
5643 is greater as the digit at the thousands place in 5643 is greater than that in 4978.
2. Compare 9364,8695,8402 and 7924
9364 is the greatest as it has the greatest digit at the thousands place in all the numbers.
Whereas 7924 is the smallest as it has the smallest digit at the thousands place in all the numbers.
3. Special case
Compare 56321 and 56843
Here, we will start by checking the thousands place.As the digit 5 at ten thousand place is same so we will move forward and see the thousands place. The digit 6 is also same so we will still move on further to check the hundreds place.
The digit at the hundreds place in 56843 is greater than that in 56321
Thus 56843 is greater than 56321
Proper Order
(a) If we arrange the numbers from the smallest to the greatest then it is said to be an Ascending order.
(b) If we arrange the numbers from the greatest to the smallest then it is said to be Descending order.
Example
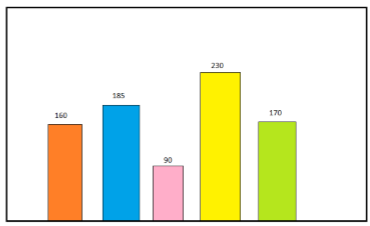
Arrange the following heights in ascending and descending order.
Ascending order – 90 < 160 < 170 < 185 < 230
Descending order – 230 >185 >170 > 160 > 90
Number Formations
Form the largest and the smallest possible numbers using 3,8,1,5 without repetition
Largest number will be formed by arranging the given numbers in descending order – 8531
The smallest number will be formed by arranging the given numbers in ascending order – 1358
Introducing 10,000
99 is the greatest 2-digit number.
999 is the greatest 3-digit number
9999 is the greatest 4-digit number
Observation
(i) If we add 1 to the greatest single digit number then we get the smallest 2-digit number
(9 + 1 = 10)
(ii) If we add 1 to the greatest 2- digit number then we get the smallest 3-digit number
(99 + 1 = 100)
(iii) If we add 1 to the greatest 3- digit number then we get the smallest 4-digit number
(999 + 1 = 1000)
Moving forward, all the above situations are same as adding 1 to the greatest 4-digit number is the same as the smallest 5-digit number. (9999 + 1 = 10,000), and it is known as ten thousand.
Place Value
It refers to the positional notation which defines a digits position.
Example
6931
Here, 1 is at one’s place, 3 is at tens place, 9 is at hundreds place and 6 is at thousands place
Expanded form
It refers to expand the number to see the value of each digit.
Example
6821 = 6000 + 800 + 20 + 1
= 6 × 1000 + 8 × 100 + 2 × 10 + 1×1
Introducing 1,00,000
As above pattern if we add 1 to the greatest 5-digit number then we will get the smallest 6-digit number
(99,999 + 1 = 1,00,000)
This number is called one lakh.
Larger Numbers
To get the larger numbers also, we will follow the same pattern.
We will get the smallest 7-digit number if we add one more to the greatest 6-digit number, which is called Ten Lakh.
Going forward if we add 1 to the greatest 7-digit number then we will get the smallest 8-digit number which is called One Crore.
Remark
1 hundred = 10 tens
1 thousand = 10 hundreds
= 100 tens
1 lakh = 100 thousands
= 1000 hundreds
1 crore = 100 lakhs
= 10,000 thousands
Pattern
9 + 1 = 10
99 + 1 = 100
999 + 1 = 1000
9,999 + 1 = 10,000
99,999 + 1 =1,00,000
9,99,999 + 1 = 10,00,000
99,99,999 + 1 = 1,00,00,000
Reading and Writing Large Numbers
We can identify the digits in ones place, tens place and hundreds place in a number by writing them under the tables O, T and H.
AS:
| Crores | Lakhs | Thousands | Ones | |||||
Ten Crores (TC) | Crores (C) | Ten Lakhs (TL) | Lakhs (L) | Ten Thousands (TTh) | Thousands (Th) | Hendreds (H) | Tens (T) | Ones (O) |
(10, 00, 00, 000) | (1,00,00,000) | (10, 00, 000) | (1,00,000) | (10,000) | (1000) | (100) | (10) | (1) |
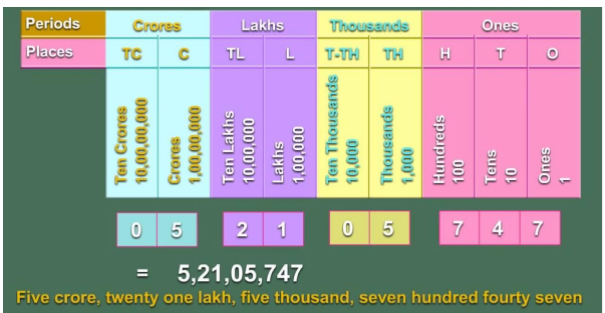
Example
Represent the number 5, 21, 05, 747
Use of Commas
We use commas in large numbers to ease reading and writing. In our Indian System of Numeration, we use ones, tens, hundreds, thousands and then lakhs and crores.
We use the first comma after hundreds place which is three digits from the right. The second comma comes after two digits i.e. five digits from the right. The third comma comes after another two digits which is seven digits from the right.
Example
5,44,12,940
Remark: We do not use commas while writing number names
International System of Numeration
| Millons | Thousands | Ones | ||||||
| Hundred Million | Ten Million | Million | Hundred Thousands | Ten Thousands | Thousands | Hundred | Tens | Ones |
| 100,000,000 | 10,000,000 | 1,000,000 | 100,000 | 10,000 | 1,000 | 100 | 10 | 1 |
Example
341,697,832
Expanded form: 3 x 100,000,000 + 4 x 10,000,000 + 1 x 1,000,000 + 6 x 100,000 + 9 x 10,000 + 7 x 1,000 + 8 x 100 + 3 x 10 + 2 x 1
Remark: If we have to express the numbers larger than a million then we use a billion in the International System of Numeration:
1 billion = 1000 million
Large Numbers in Practice
10 millimeters = 1 centimeter
1 meter = 100 centimeters
= 1000 millimeters
1 kilometer = 1000 meters
1 kilogram = 1000 grams.
1 gram = 1000 milligrams
. 1 litre = 1000 millilitres
1 litre = 1000 millilitres
Let’s Solve Some Problems
Example: 1
To fill an order, the factory dyed 336 yards of silk in yellow and 37 yards in pink. How many yards of silk did it dye for that order?
Solution:
Yards of yellow silk = 336
Yards of pink silk = 37
Total yards of silk dyed = 336 + 37
= 371
Thus, 371 yards of silk was dyed for the order.
Example: 2
There are 8797 children in a town, 6989 go to school. How many children do not go to school?
Solution:
Total children = 8797
Children who go to school = 6989
Children who do not go to school = 8797 – 6989
= 1808
Thus 1808 children of the town do not go to school.
Example: 3
There are 24 folders and each has 56 sheets of paper inside them. How many sheets of paper are there altogether?
Solution:
Thus there are 1344 sheets of paper altogether.
Example: 4
$5,876 is distributed equally among 26 men. How much money will each person get?
Solution:
Money received by 26 men = 5876
Money received by one man = 5876 ÷ 26
Thus each man got $226.
Estimation
It is a rough calculation of value. We use estimations when we have to deal with large numbers and to do the quick calculations.
Estimating to the nearest tens by rounding off
If the digit in the ones places is:
5 or higher, round tens place up
4 or lower, leave tens place as is
Firstly to estimate we need to see where does the number lies.
Here 38 lie between 30 and 40
Secondly, we will see if it is 5 or higher.
Yes it is higher than 5 i.e. 38
Thus the number 738 is rounded off to 740.
Estimating to the nearest hundreds by rounding off
Round off the number 867 nearest to the hundreds.
It lies between 800 and 900
Now we have to check for tens place. If it is greater than 50 then we will round it off to the upper side and if it is less than 50 then we will round it off on the lower side.
It is 67, which is greater than 50 and is closer to 900.
Thus 867 is rounded off to 900
Estimating to the nearest thousands by rounding off
The Numbers from 1 to 499 are rounded off to 0 as they are nearer to 0, and the numbers from 501 to 999 are rounded off to 1000 as they are nearer to 1000
And 500 is always rounded off to 1000.
Example
Round off the number 7690 nearest to thousands.
It lies between 7000 and 8000
And is closer to 8000
Thus 7690 is rounded off to 8000.
To estimate sum or difference
Estimate: 3,210 + 12,884
Solution
3,210 will be rounded off to 3000.
12,884 will be rounded off to 13000.
3000+ 13000
Estimated solution = 16000
Actual solution = 3,210 + 12 884
= 16,094
To estimate products
Estimate: 73 × 18
Solution
73 will be rounded off to 70
18 will be rounded off to 20
70 × 20
Estimated solution = 1400
Actual solution = 73 × 18
= 1314
Using Brackets
We use brackets to indicate that the numbers inside should be treated as a different number thus the bracket should be solved first.
Example
8 + 2 = 8 + 10
= 18
Whereas if we use brackets
(8 + 2) × 5 = 10
= 50
Expanding brackets
Brackets help in the systematic calculation.
Example
3 × 109 = 3 × (100 + 9)
= 3 × 100 + 3 × 9
= 300 + 27
= 327
Roman Numerals
Numbers in this system are represented by combinations of letters from the Latin alphabets.
Rules:
a. If we repeat a symbol, its value will be added as many times as it occurs:
Example
II is equal 2
XX is 20
XXX is 30.
b. We cannot repeat a symbol more than three times and some symbols like V, L and D can never be repeated.
c. If we write a symbol of lesser value to the right of a symbol of larger value then its value will be added to the value of the greater symbol.
VI = 5 + 1 = 6, XII = 10 + 2 = 12 and LXV = 50 + 10 + 5 = 65.
d. If we write a symbol of lesser value to the left of a symbol of larger value then its value will be subtracted from the value of the greater symbol.
IV = 5 – 1 = 4, IX = 10 – 1 = 9 XL= 50 – 10 = 40, XC = 100 – 10 = 90.
e. The symbols V, L and D can never be subtracted so they are never written to the left of a symbol of greater value. We can subtract the symbol “I” from V and X only and the symbol X from L, M and C only.


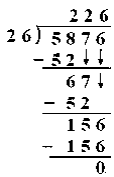


Hello ma’am
I want handwritten notes with concepts of ncert math from classes 6th to 10th new revised syllabus accordingly.
Thank you