Notes For All Chapters Maths Class 6
Plane Figures
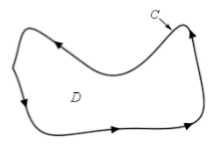
The closed 2-D shapes are referred to as plane figures.
Here “C” is the boundary of the above figure and the area inside the boundary is the region of this figure. Point D comes in the area of the given figure.
Perimeter
If we go around the figure along its boundary to form a closed figure then the distance covered is the perimeter of that figure. Hence the Perimeter refers to the length of the boundary of a closed figure.
If a figure is made up of line segments only then we can find its perimeter by adding the length of all the sides of the given figure.
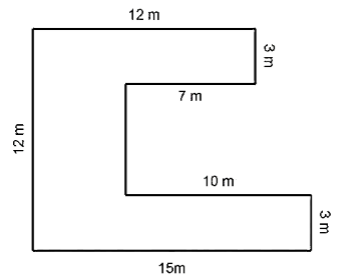
Example
Find the Perimeter of the given figure.
Solution
Perimeter = Sum of all the sides
= (12 + 3 + 7 + 6 + 10 + 3 + 15 + 12) m
= 68 m
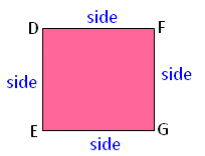
The Perimeter of a Rectangle
A rectangle is a closed figure with two pairs of equal opposite sides.
Perimeter of a rectangle = Sum of all sides
= length + breadth + length + breadth
Thus, Perimeter of a rectangle = 2 × (length + breadth)
Example: 1
The length and breadth of a rectangular swimming pool are 16 and 12 meters respectively .find the perimeter of the pool.
Solution:
Perimeter of a rectangle = 2 × (length + breadth)
Perimeter of the pool = 2 × (16 + 12)
= 2 × 28
= 56 meters
Example: 2
Find the cost of fencing a rectangular farm of length 24 meters and breadth 18 meters at 8/- per meter.
Solution:
Perimeter of a rectangle = 2 × (length + breadth)
Perimeter of the farm = 2 × (24 + 18)
= 2 × 42
= 84 meter
Cost of fencing = 84 × 8
= Rs. 672
Thus the cost of fencing the farm is Rs. 672/-.
Regular Closed Figure
Figures with equal length of sides and an equal measure of angles are known as Regular Closed Figures or Regular Polygon.
Perimeter of Regular Polygon = Number of sides × Length of one side
Perimeter of Square
Square is a regular polygon with 4 equal sides.
Perimeter of square = side + side + side + side
Thus, Perimeter of a square = 4 × length of a side
Example
Find the perimeter of a square having side length 25 cm.
Solution
Perimeter of a square = 4 × length of a side
Perimeter of square = 4 × 25
= 100 cm
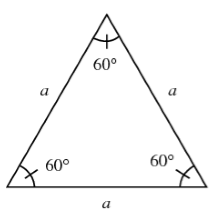
Perimeter of an Equilateral Triangle
An equilateral triangle is a regular polygon with three equal sides and angles.
Perimeter of an equilateral triangle = 3 × length of a side
Example
Find the perimeter of a triangle having each side length 13 cm.
Solution
Perimeter of an equilateral triangle = 3 × length of a side
Perimeter of triangle = 3 × 13
= 39 cm
Perimeter of a Regular Pentagon
A regular pentagon is a polygon with 5 equal sides and angles.
Perimeter of a regular pentagon = 5 × length of one side
Example
Find the perimeter of a pentagon having side length 9 cm.
Solution
Perimeter of a regular pentagon = 5 × length of one side
Perimeter of a regular pentagon = 5 × 9
= 45 cm
Perimeter of a Regular Hexagon
A regular hexagon is a polygon with 6 equal sides and angles.
Perimeter of a regular hexagon = 6 × Length of one side
Example
Find the perimeter of a hexagon having side length 15cm.
Solution
Perimeter of a regular hexagon = 6 × Length of one side
Perimeter of a regular hexagon = 6 × 15
= 90 cm
Perimeter of a Regular Octagon
A regular octagon is a polygon with 8 equal sides and angles.
Perimeter of a regular octagon = 8 × length of one side
Example
Find the perimeter of an octagon having side length 7cm.
Solution
Perimeter of a regular octagon = 8 × length of one side
Perimeter of a regular octagon = 8 × 7
= 56 cm
Area
Area refers to the surface enclosed by a closed figure.
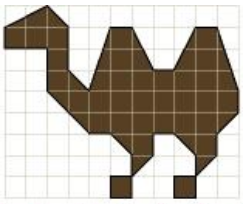
To find the area of any irregular closed figure, we can put them on a graph paper with the square of 1 cm × 1 cm .then estimate the area of that figure by counting the area of the squares covered by the figure.
Here one square is taken as 1 sq.unit.
Example
Find the area of the given figure. (1 square = 1 m²)
Solution
The given figure is made up of line segments and is covered with some full squares and some half squares.
Full squares in figure = 32
Half squares in figure = 21
Area covered by full squares = 32 × 1 sq. unit = 32 sq. unit.
Area covered by half squares = 21 × (1/2) sq. unit. = 10.5 sq. unit.
Total area covered by figure = 32 + 10.5 = 42.5 sq. unit.
Area of a Rectangle
Area of a rectangle = (length × breadth)
Example
Find the area of a rectangle whose length and breadth are 20 cm and 12 cm respectively.
Solution
Length of the rectangle = 20 cm
Breadth of the rectangle = 12 cm
Area of the rectangle = length × breadth
= 20 cm × 12 cm
= 240 sq cm.
To find the length of a rectangle if breadth and area are given:
Example
What will be the length of the rectangle if its breadth is 6 m and the area is 48sq.m?
Solution
Length = 48/6
= 8 m
To find the breadth of the rectangle if length and area are given:
Example
What will be the breadth of the rectangle if its length is 8 m and the area is 81 sq.m?
Solution
Breadth = 81/8
= 9 m
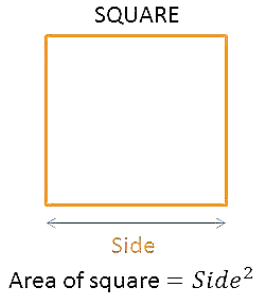
Area of a Square
Area of a square is the region covered by the boundary of a square.
Area of a square = side × side
Example
Calculate the area of a square of side 13 cm.
Solution
Area of a square = side × side
= 13 × 13
= 169 cm².

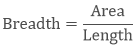
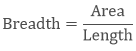

VERY GOOD