Notes For All Chapters Maths Class 6
Symmetry
When we fold a paper in such a way that the picture is divided into two equal halves then the line which divides the picture into two halves is called a Line of Symmetry.
Here the line divides the star into two halves so it is the line of symmetry. It is also called the Mirror Line because if we place the mirror on that line then one side of the picture will fall exactly on the other side of the picture.
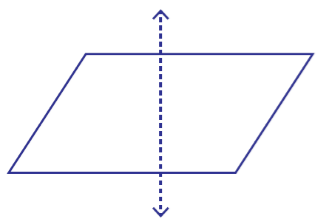
Non-symmetrical Figure
This figure is not symmetrical as if we fold the image from the dotted line then it does not divide it into two equal halves.
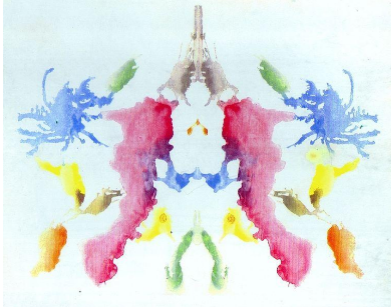
Making Symmetric Figures: Ink-blot Devils
To make an ink-blot pattern-
(i) Take a piece of paper and fold it in half.
(ii) Put some drops of ink on one side of the paper.
(iii) Then press the halves together.
(iv) It will make a symmetric pattern with the fold as the line of symmetry.
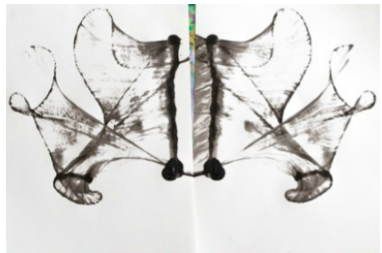
Inked-string pattern
To make an inked string pattern-
(i) Take a piece of paper and fold it in half.
(ii) Dip a string in different colours and arrange it on the one side of the paper.
(iii) Press the two halves together and pull the string.
(iv) It will make a symmetric inked string pattern with the fold as the line of symmetry.
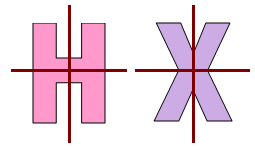
Two Lines of Symmetry
Some figures have two lines of symmetry.
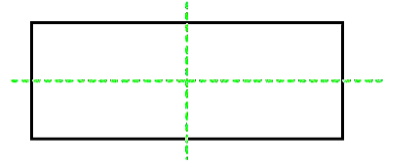
1. A Rectangle
Take a rectangular sheet and fold it horizontally in two equal halves and then again fold it vertically in two equal halves. After opening it, we get two lines of symmetry of the rectangular sheet.
2. More Figures with two Line of Symmetry
If we take a rectangular piece of paper and double fold it to make two lines of symmetry and cut it in some new shape then after opening it we will get a new image that too with the two lines of symmetry.
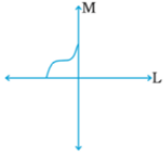
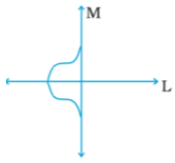
Construction of figure with two Lines of Symmetry
1. To draw a figure with two lines of symmetry, take one figure.
2. Let L and M be the two lines of symmetry.
3. Draw the figure in such a way that L is the line of symmetry,
4. Now complete the figure by drawing the remaining part so that M will also become the line of symmetry.
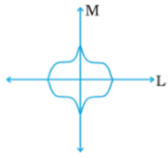
Hence this is the final figure with two lines of symmetry.
Multiple Lines of Symmetry
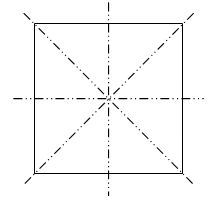
Take a square sheet of paper and fold it in two halves vertically and again horizontally .open it and fold it in two equal halves diagonally then again open it and fold it along another diagonal.
When you will open the paper you will see four imaginary lines and these lines are the lines of symmetry.
Some more images with more than two lines of symmetry
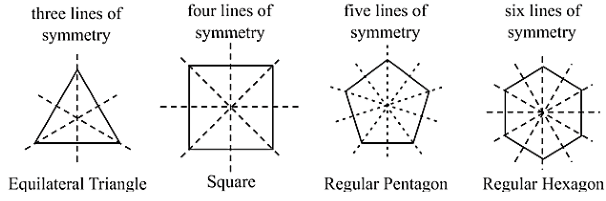
(i) Equilateral triangle will have three lines of symmetry.
(ii) Square will have four lines of symmetry.
(iii) Regular pentagon will have five lines of symmetry.
(iv) Regular hexagon will have six lines of symmetry.
Some Real-life Examples of Symmetry
In Taj Mahal and the butterfly there is one line of symmetry and there are so many other things also in our daily life which are having one or more line of symmetry.
Reflection and Symmetry
The line of symmetry is also called Mirror Line because the mirror image of an object is symmetrical to the image. When we see an object in the mirror then there is no change in the length and angles of the object except one thing i.e. the image is opposite to the original image.
Some Examples of Reflection Symmetry
1. Paper Decoration
We can use a rectangular sheet to fold and create some intricate patterns by cutting paper.
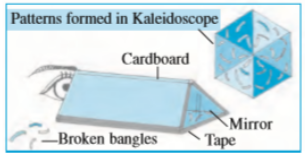
2. Kaleidoscope
In Kaleidoscope, mirrors are used to create pictures having various lines of symmetry. Two mirrors strips forming a V-shape are used. The angle between the mirrors determines the number of lines of symmetry.
Example
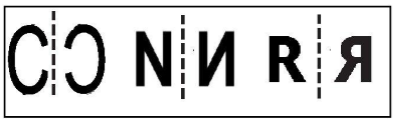
Which alphabet will remain same after reflection symmetry? Check for R, C, N, A and T.
Solution
In the alphabet reflection symmetry, the alphabets look opposite in the mirror i.e. the alphabet written from right to left will appear as written from left to right.
Hence C, N and R will not look the same after reflection.
Hence A and T will look same after reflection symmetry.







Leave a Reply