Notes For All Chapters Maths Class 6
Natural Numbers
All the positive counting numbers starting from one are called Natural Numbers.
Predecessor and Successor
If we add 1 to any natural number, we get the next number, which is called the Successor of that number.
12 + 1 = 13
So 13 is the successor of 12.
If we subtract 1 from any natural number, we get the predecessor of that number.
12 – 1 = 11
So 11 is the predecessor of 12.
Remark: There is no predecessor of 1 in natural numbers.
Whole Numbers
Whole numbers are the collection of natural numbers including zero. So, the zero is the predecessor of 1 in the whole numbers.
Number Line
To draw a number line, follow these steps-
(i) Draw a line and mark a point 0 on it.
(ii) Now mark the second point to the right of zero and label it as 1.
(iii) The distance between the 0 and 1 is called the unit distance.
(iv) Now you can mark other points as 2, 3, 4 and so on with the unit distance.
This is the number line for the whole numbers.
1. The distance between two points
The distance between 3 and 5 is 2 units. Likewise, the distance between 1 and 6 is 5 units.
2. The greater number on the number line
The number on the right is always greater than the number on the left.
As number 5 is on the right of the number 2, Hence 5>2.
3. A smaller number on the number line
The number on the left of any number is always smaller than that number.
As number 3 is on the left of 7, so 3 < 7.
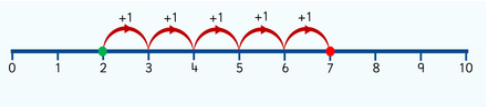
Addition on the Number Line
If we have to add 2 and 5, then start with 2 and make 5 jumps to the right. As our 5th jump is at 7 so the answer is 7.
The sum of 2 and 5 is 2 + 5 = 7
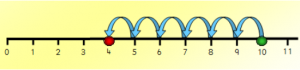
Subtraction on the Number Line
If we have to subtract 6 from 10, then we have to start from 10 and make 6 jumps to the left. As our 6th jump is at 4, so the answer is 4.
The subtraction of 6 from 10 is 10 – 6 = 4.
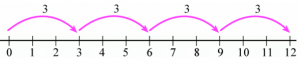
Multiplication on the Number Line
If we have to multiply 4 and 3, then Start from 0, make 4 jumps using 3 units at a time to the right, as you reach to 12. So, we say, 3 × 4 = 12.

Properties of Whole Numbers
1. Closure Property
Two whole numbers are said to be closed if their operation is also the whole number.
| Operation | Meaning | Example | Closed or not |
Addition | Whole numbers are closed under addition as their sum is also a whole number. | 2 + 5 = 7 | Yes |
Subtraction | Whole numbers are not closed under subtraction as their difference is not always a whole number. | 9 – 2 = 7 2 – 9 = (-7) which is not a whole number. | No |
Multiplication | Whole numbers are closed under multiplication as their product is also a whole number. | 9 × 5 = 45 | Yes |
Division | Whole numbers are not closed under division as their result is not always a whole number. | 5 ÷ 1 = 5 5 ÷ 2 =, not a whole number. | No |
2. Commutative Property
Two whole numbers are said to be commutative if their result remains the same even if we swap the positions of the numbers.
| Operation | Meaning | Example | Commutative or not |
| Addition | The addition is commutative for whole numbers as their sum remains the same even if we interchange the position of the numbers. | 2 + 5 = 7 5 + 2 = 7 | Yes |
| Subtraction | Subtraction is not commutative for whole numbers as their difference may be different if we interchange the position of the numbers. | 9 – 2 = 7 2 – 9 = (-7) which is not a whole number. | No |
| Multiplication | Multiplication is commutative for whole numbers as their product remains the same even if we interchange the position of the numbers. | 9 × 5 = 45 5 × 9 = 45 | Yes |
| Division | The division is not commutative for whole numbers as their result may be different if we interchange the position of the numbers. | 5 ÷ 1 = 5 1 ÷ 5 =, not a whole number. | No |
3. Associative Property
The two whole numbers are said to be associative if the result remains the same even if we change the grouping of the numbers.
| Operation | Meaning | Example | Associative or not |
| Addition | The addition is associative for whole numbers as their sum remains the same even if we change the grouping of the numbers. | 3 + (2 + 5) = (3 + 2) + 5 3 + 7 = 5 + 5 10 = 10 | Yes |
| subtraction | Subtraction is not associative for whole numbers as their difference may change if we change the grouping of the numbers. | 8 – (10 – 2) ≠ (8 – 10) – 2 8 – (8) ≠ (-2) – 2 0 ≠ (-4) | No |
| Multiplication | Multiplication is associative for whole numbers as their product remains the same even if we change the grouping of the numbers. | 3 × (5 × 2) = (3 × 5) × 2 3 × (10) = (15) × 2 30 = 30 | Yes |
| Division | The division is not associative for whole numbers as their result may change if we change the grouping of the numbers. | 24 ÷ 3 ≠ 4 ÷ 2 8 ≠ 2 | No |
4. Distributivity of Multiplication over Addition
This property says that if we have three whole numbers x, y and z, then
x(y + z) = xy + xz
Example
Evaluate 15 × 45
Solution
15 × 45 = 15 × (40 + 5)
= 15 × 40 + 15 × 5
= 600 + 75
= 675
5. Identity for Addition
If we add zero to any whole number the result will the same number only. So zero is the additive identity of whole numbers.
a + 0 = 0 + a = a
This clearly shows that if we add zero apples to 2 apples we get the two apples only.
6. Identity for Multiplication
If we multiply one to any whole number the result will be the same whole number. So one is the multiplicative identity of whole numbers.
Patterns
Patterns are used for easy verbal calculations and to understand the numbers better.
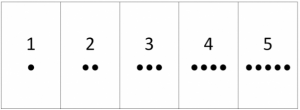
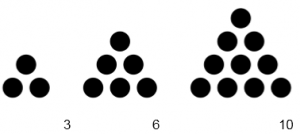
We can arrange the numbers using dots in elementary shapes like triangle, square, rectangle and line.
1. We can arrange every number using dots in a line
2. We can arrange some numbers using a rectangle.
3. We can arrange some numbers using a square.
4. We can arrange some numbers using a triangle.
Use of Patterns
Patterns can be used to simplify the process.
1. 123 + 9 = 123 + 10 – 1 = 133 -1 = 132
123 + 99 = 123 + 100 – 1 = 223 – 1 = 222
2. 83 × 9 = 83 × (10-1) = 830 – 83 = 747
83 × 99 = 83 × (100-1) = 8300 – 83 = 8217


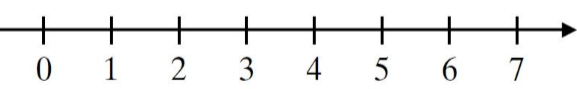

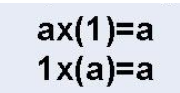



Leave a Reply