Solutions For All Chapters Maths Class 8
Ex 11.1 Class 8 Maths Question 1.
Following are the car parking charges near a railway station up to.
4 hours – ₹ 60
8 hours – ₹ 100
12 hours – ₹ 140
24 hours – ₹ 180
Check if the parking charges are in direct proportions to the parking time.
Solution:
We have the ratio of time period and the parking charge.
Hence the given quantities are not directly proportional.
Ex 11.1 Class 8 Maths Question 2.
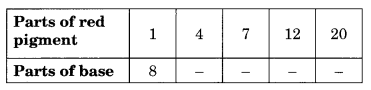
A mixture of paint is prepared by mixing 1 part of red pigments with 8 parts of base. In the following table, find the parts of base that need to be added.
Solution:
Let the number to be filled in the blanks be a, b, c and d respectively.
Ex 11.1 Class 8 Maths Question 3.
In Question 2 above, if 1 part of a red pigment requires 75 mL of base, how much red pigment should we mix with 1800 mL of base?
Solution:
Let the required red pigment be x part.
Hence, the required amount of red pigment = 24 parts.
Ex 11.1 Class 8 Maths Question 4.
A machine in a soft drink factory fills 840 bottles in six hours. How many bottles will it fill in five hours?
Solution:
Let the required number of bottles be x
Hence the required number of bottles = 700.
Ex 11.1 Class 8 Maths Question 5.
A photograph of a bacteria enlarged 50,000 times attains a length of 5 cm as shown in the diagram. What is the actual length of the bacteria? If the photograph is enlarged 20,000 times only, what would be its enlarged length?
Solution:
Let the actual length be x cm.
Ex 11.1 Class 8 Maths Question 6.
In a model of a ship, the mast is 9 cm high, while the mast of the actual ship is 12 m high. If the length of the ship is 28 m, how long is the model ship?
Solution:
Let the required length of the model ship be x m.
Ex 11.1 Class 8 Maths Question 7.
Suppose 2 kg of sugar contains 9 × 106 crystals. How many sugar crystals are there in
(i) 5 kg of sugar?
(ii) 1.2 kg of sugar?
Solution:
Let x be the number of sugar crystals needed.
Ex 11.1 Class 8 Maths Question 8.
Rashmi has a road map with a scale of 1 cm representing 18 km. She drives on a road of 72 km. What would be her distance covered in the map?
Solution:
Let the required distance be x km.
Hence the distance covered in the map = 4 cm.
Ex 11.1 Class 8 Maths Question 9.
A 5 m 60 cm high vertical pole casts a shadow 3 m 20 cm long. Find at the same time
(i) the length of the shadow cast by another pole 10 m 50 cm high,
(ii) the height of a pole which casts a shadow 5 m long.
Solution:
(i) Let the required length of shadow be x m.
Ex 11.1 Class 8 Maths Question 10.
A loaded truck travels 14 km in 25 minutes. If the speed remains the same, how far can it travel in 5 hours?
Solution:
Let the required distance be x km.
Hence the required distance = 168 km.
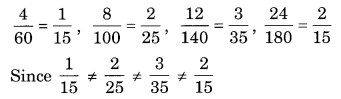

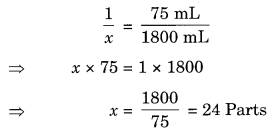


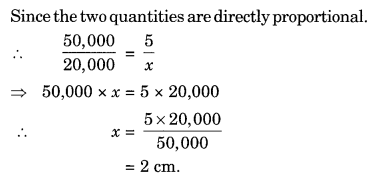

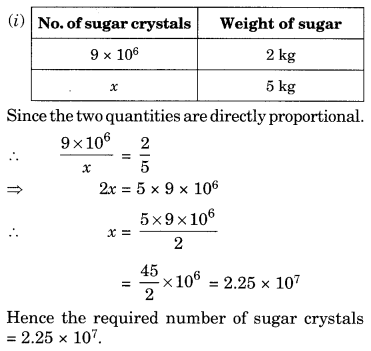
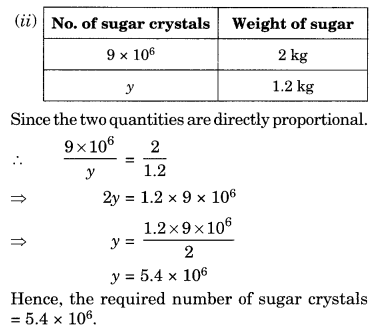





It’s a great website for students to pass….
Thanks
I love it very much evidyarthi
Evidyarthi, I kindly request you to provide one-word answers to the questions.
Very nice, Evidyarthi! I am proud of you! 👏😊
I really like your solutions
This helps me so much. Thanks for it.
Thank you for your information
Give some very short solution these are very big