Solutions For All Chapters Maths Class 8
Ex 8.3 Class 8 Maths Question 1.
Carry out the multiplication of the expressions in each of the following pairs:
(i) 4p, q + r
(ii) ab, a – b
(iii) a + b, 7a²b²
(iv) a² – 9, 4a
(v) pq + qr + rp, 0
Solution:
(i) 4p × (q + r) = (4p × q) + (4p × r) = 4pq + 4pr
(ii) ab, a – b = ab × (a – b) = (ab × a) – (ab × b) = a²b – ab²
(iii) (a + b) × 7a²b² = (a × 7a²b²) + (b × 7a²b²) = 7a³b² + 7a²b³
(iv) (a² – 9) × 4a = (a² × 4a) – (9 × 4a) = 4a³ – 36a
(v) (pq + qr + rp) × 0 = 0
[∵ Any number multiplied by 0 is = 0]
Ex 8.3 Class 8 Maths Question 2.
Complete the table.
| S.No. | First Expression | Second Expression | Product |
| (i) | a | b + c + d | – |
| (ii) | x + y – 5 | 5xy | – |
| (iii) | p | 6p2 – 7p + 5 | – |
| (iv) | 4p2q2 | p2 – q2 | – |
| (v) | a + b + c | abc | – |
Solution:
(i) a × (b + c + d) = (a × b) + (a × c) + (a × d) = ab + ac + ad
(ii) (x + y – 5) (5xy) = (x × 5xy) + (y × 5xy) – (5 × 5xy) = 5x²y + 5xy² – 25xy
(iii) p × (6p² – 7p + 5) = (p × 6p²) – (p × 7p) + (p × 5) = 6p³ – 7p² + 5p
(iv) 4p²q² × (p² – q²) = 4p²q² × p2 – 4p²q² × q² = 4p4q² – 4p²q4
(v) (a + b + c) × (abc) = (a × abc) + (b × abc) + (c × abc) = a²bc + ab²c + abc²
Completed Table:
| S.No. | First Expression | Second Expression | Product |
| (i) | a | b + c + d | ab + ac + ad |
| (ii) | x + y – 5 | 5xy | 5x2y + 5xy2 – 25xy |
| (iii) | p | 6p2 – 7p + 5 | 6p3 – 7p2 + 5p |
| (iv) | 4p2q2 | p2 – q2 | 4p4q2 – 4p2q4 |
| (v) | a + b + c | abc | a2bc + ab2c + abc2 |
Ex 8.3 Class 8 Maths Question 3.
Find the products.
Solution:
Ex 8.3 Class 8 Maths Question 4.
(a) Simplify: 3x(4x – 5) + 3 and find its values for (i) x = 3 (ii) x = 1/2.
(b) Simplify: a(a² + a + 1) + 5 and find its value for (i) a = 0 (ii) a = 1 (iii) a = -1
Solution:
(a) We have 3x(4x – 5) + 3 = 4x × 3x – 5 × 3x + 3 = 12x² – 15x + 3
(i) For x = 3, we have
12 × (3)² – 15 × 3 + 3 = 12 × 9 – 45 + 3 = 108 – 42 = 66
(b) We have a(a2 + a + 1) + 5
= (a2 × a) + (a × a) + (1 × a) + 5
= a3 + a2 + a + 5
(i) For a = 0, we have
= (0)3 + (0)2 + (0) + 5 = 5
(ii) For a = 1, we have
= (1)3 + (1)2 + (1) + 5 = 1 + 1 + 1 + 5 = 8
(iii) For a = -1, we have
= (-1)3 + (-1)2 + (-1) + 5 = -1 + 1 – 1 + 5 = 4
Ex 8.3 Class 8 Maths Question 5.
(a) Add: p(p – q), q(q – r) and r(r – p)
(b) Add: 2x(z – x – y) and 2y(z – y – x)
(c) Subtract: 3l(l – 4m + 5n) from 4l(10n – 3m + 2l)
(d) Subtract: 3a(a + b + c) – 2b(a – b + c) from 4c(-a + b + c)
Solution:
(a) p(p – q) + q(q – r) + r(r – p)
= (p × p) – (p × q) + (q × q) – (q × r) + (r × r) – (r × p)
= p2 – pq + q2 – qr + r2 – rp
= p2 + q2 + r2 – pq – qr – rp
(b) 2x(z – x – y) + 2y(z – y – x)
= (2x × z) – (2x × x) – (2x × y) + (2y × z) – (2y × y) – (2y × x)
= 2xz – 2x2 – 2xy + 2yz – 2y2 – 2xy
= -2x2 – 2y2 + 2xz + 2yz – 4xy
= -2x2 – 2y2 – 4xy + 2yz + 2xz
(c) 4l(10n – 3m + 2l) – 3l(l – 4m + 5n)
= (4l × 10n) – (4l × 3m) + (4l × 2l) – (3l × l) – (3l × -4m) – (3l × 5n)
= 40ln – 12lm + 8l2 – 3l2 + 12lm – 15ln
= (40ln – 15ln) + (-12lm + 12lm) + (8l2 – 3l2)
= 25ln + 0 + 5l2
= 25ln + 5l2
= 5l2 + 25ln
(d) [4c(-a + b + c)] – [3a(a + b + c) – 2b(a – b + c)]
= (-4ac + 4bc + 4c2) – (3a2 + 3ab + 3ac – 2ab + 2b2 – 2bc)
= -4ac + 4bc + 4c2 – 3a2 – 3ab – 3ac + 2ab – 2b2 + 2bc
= -3a2 – 2b2 + 4c2 – ab + 6bc – 7ac
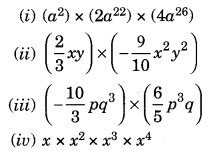
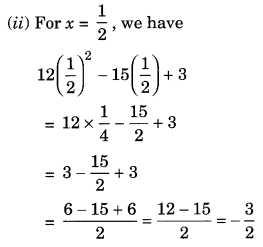

I have a great solution 😊
Good website
Good
👍👍
Good solutions
Great 👍👍👍
Solution with the explanation 🙂
100 rs ka redem coda dedo
Yes working
their is so many unonted steps the sum but answer are
aquret this is good and try
to reduce some unonted steps from the sums
Thank you !10