Patterns and Properties of Perfect Squares (Page 4)
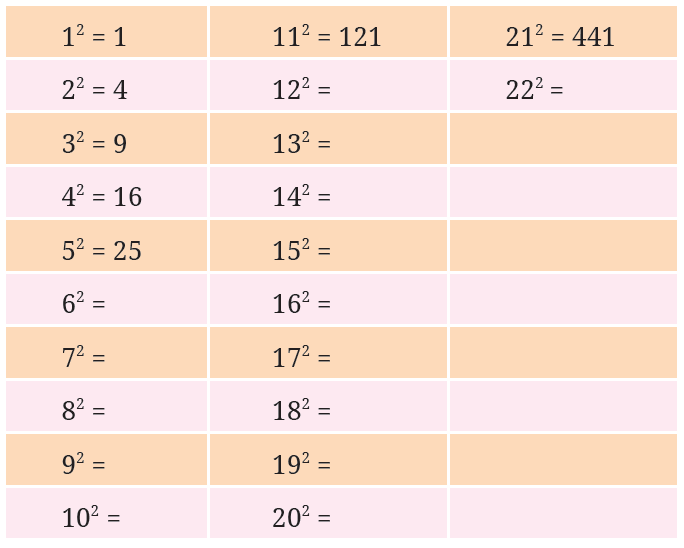
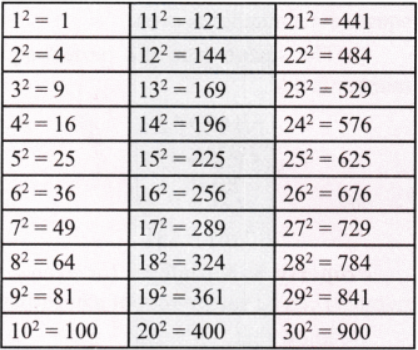
Q. 1 Find the squares of the first 30 natural numbers and fill in the table below.
Answer:
Q 2. What patterns do you notice? Share your observations and make conjectures.
Answer: When we look at the squares of the first 30 natural numbers, we notice some patterns:
1. Unit digits pattern
- The squares always end with 0, 1, 4, 5, 6, or 9.
- They never end with 2, 3, 7, or 8.
2. Even/Odd relation
- The square of an even number is always even.
- The square of an odd number is always odd.
3. Zeros at the end
- If a number has a zero at the end, its square will have two zeros at the end.
- In general, squares always have an even number of zeros at the end.
4. Increasing difference
The difference between two consecutive squares is always an odd number (e.g., 4 – 1 = 3, 9 – 4 = 5, 16 – 9 = 7, …).
Conjecture (what we can guess from the pattern)
- If a number ends with 2, 3, 7, or 8, it cannot be a perfect square.
- Every square number can be written as the sum of consecutive odd numbers.
Q 3. If a number ends in 0, 1, 4, 5, 6 or 9, is it always a square?
Answer: No, if a number ends in 0, 1, 4, 5, 6 or 9, it is not always a square.
For example: 16 and 36 are squares ending in 6, but 26 also ends in 6 and is not a square.
What we can say for sure:
If a number ends with 2, 3, 7, or 8 → it can never be a perfect square.
Q 4. Write 5 numbers such that you can determine by looking at their units digit that they are not squares.
numbers ending with 2, 3, 7, 8 can never be perfect squares.
Examples: 12, 23, 37, 48, 52
Answer: 12, 23, 37, 48, 52
The squares, 1², 9², 11², 19², 21², and 29², all have 1 in their units place. Write the next two squares. Notice that if a number has 1 or 9 in the units place, then its square ends in 1.
31² = 961 → units digit 1
39² = 1521 → units digit 1
Answer: 31² = 961, 39² = 1521
So final answers:
- Five numbers not squares (by unit digit): 12, 23, 37, 48, 52
- Next two squares ending with 1: 31² = 961, 39² = 1521
Q 5. Let us consider square numbers ending in 6: 16 = 4², 36 = 6², 196 = 14², 256 = 16², 576 = 24², and 676 = 26².
Which of the following numbers have the digit 6 in the units place?
(i) 38²
(ii) 34²
(iii) 46²
(iv) 56²
(v) 74²
(vi) 82²
Let’s solve step by step and check the units digit of each square:
(i) 38² = 1444 → units digit = 4 ❌
(ii) 34² = 1156 → units digit = 6 ✅
(iii) 46² = 2116 → units digit = 6 ✅
(iv) 56² = 3136 → units digit = 6 ✅
(v) 74² = 5476 → units digit = 6 ✅
(vi) 82² = 6724 → units digit = 4 ❌
Answer: 34², 46², 56², 74²
Q 6. Find more such patterns by observing the numbers and their squares from the table you filled earlier.
Consider the following numbers and their squares.
Answer:
If a number has a 3 or 9 in the units place, its square will always end in 6.
If a number has a 2 or 8 in the units place, its square will always end in 4.
If a number has a 5 in the units place, its square will always end in 5.
Q 7. If a number contains 3 zeros at the end, how many zeros will its square have at the end?
Answer: If a number contains 3 zeros at the end, then its square will have 6 zeros at the end.
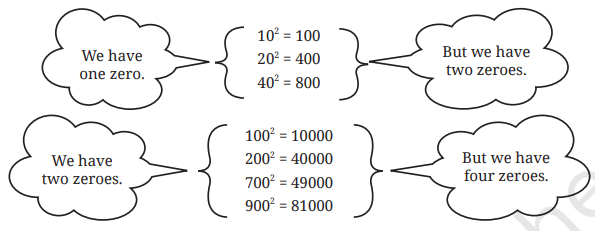
Q 8. What do you notice about the number of zeros at the end of a number and the number of zeros at the end of its square? Will this always happen? Can we say that squares can only have an even number of zeros at the end?
Answer: From the table, we notice that whenever a two-digit number has a zero in the units place, its square ends with two zeros. This is not just a coincidence but a rule.
In general, if a number ends with n zeros, then its square will always end with 2n zeros.
Therefore, we can conclude that the square of any number ending in zero will always have an even number of zeros at the end.
Q 9. What can you say about the parity of a number and its square?
Answer:
If a number is even, then its square will also be even.
Example: 6² = 36 (even).
If a number is odd, then its square will also be odd.
Example: 7² = 49 (odd).
So, the parity (odd/even nature) of a number and its square is always the same.
Perfect Squares and Odd Numbers
Q. Find how many numbers lie between two consecutive perfect squares.
Do you notice a pattern?
Answer:
There are exactly 2n numbers between n² and (n+1)².
For example: Between 3² = 9 and 4² = 16,the numbers are 10, 11, 12, 13, 14, 15.
So, there are 2 × 3 = 6 numbers.
Pattern: The number of integers between two consecutive perfect squares keeps increasing by 2 as
n increases.
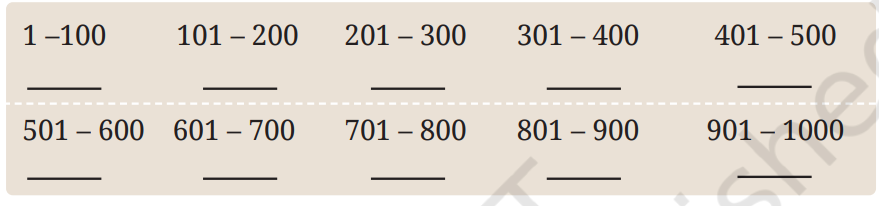
Q. How many square numbers are there between 1 and 100? How many are between 101 and 200? Using the table of squares you filled earlier, enter the values below, tabulating the number of squares in each block of 100. What is the largest square less than 1000?
Answer:
The largest square less than 1000 is 31² = 961.
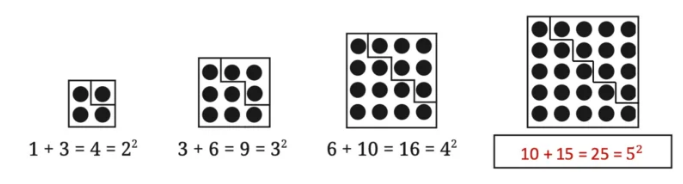
Perfect Squares and Triangular Numbers
Q. Can you see any relation between triangular numbers and square numbers? Extend the pattern shown and draw the next term.
Answer:
Square Roots
Q. Find whether 1156 and 2800 are perfect squares using prime factorisation.
Answer:
(i) 1156 = (2 × 2) × (17 × 17)
= 2²× 17²
= (2 × 17)²
= (34)²
∴ √1156 = 34.
(ii) 2800 = (2 × 2) × (2 × 2) × (5 × 5) × 7
= 2² × 2² × 5² × 7
Since the factors cannot be paired
∴ 2800 is not a perfect square.
Figure it Out
1. Which of the following numbers are not perfect squares?
(i) 2032 (ii) 2048 (iii) 1027 (iv) 1089
Answer:
(i) 2032 is not a perfect square, as a number ending with 2 can not be a perfect square.
(ii) 2048 is not a perfect square, as a number ending with 8 can not be a perfect square.
(iii) 1027 is not a perfect square, as a number ending with 7 can not be a perfect square.
(iv) 1089 ends in 9 at the unit’s place. Hence, it is a perfect square.
2. Which one among 64² , 108², 292², 36² has last digit 4?
64² = 4096 → ends with 6
108² = 11664 → ends with 4 ✅
292² = 85264 → ends with 4 ✅
36² = 1296 → ends with 6
Answer: 108² and 292²
3. Given 125² = 15625, what is the value of 126².
(i) 15625 + 126
(ii) 15625 + 26²
(iii) 15625 + 253
(iv) 15625 + 251
(v) 15625 + 51²
Answer:
We use the formula:
(n+1)² = n² + 2n + 1
Here, n = 125.
126² = 125² + 2(125) + 1
126² = 15625 + 250 + 1
126² = 15625 + 251
So the correct option is: (iv) 15625 + 251
4. Find the length of the side of a square whose area is 441 m².
Answer:
Area of the square = side × side = 441 m².
(side)² = 441
side = √441
side = ± 21 m
Since the side of a square cannot be negative, the length of the side of the square is 21 m.
5. Find the smallest square number that is divisible by each of the following numbers: 4, 9, and 10.
Answer:
Factorise the numbers
4 = 2²
9 = 3²
10 = 2 × 5
Find the LCM
Take the highest powers of each prime factor:
LCM (4,9,10) = 2² × 3² × 5 = 180
Make it a perfect square
Prime factorisation of 180 = 2² × 3² × 5.
To be a perfect square, each prime factor must appear in even powers.
Here,5 appears only once → we need one more 5.
So, smallest perfect square divisible by 4, 9, 10 is: 180 × 5 = 900
6. Find the smallest number by which 9408 must be multiplied so that the product is a perfect square. Find the square root of the product.
Answer:
To find the smallest number by which 9408 must be multiplied so that the product is a perfect square, we first need to find the prime factorization of 9408 and check whether its prime factors can be divided into two equal groups.
Prime factorisation of 9408: \(2^6\) × 3 × 7²
Here, 3 appears only once, so we multiply 9408 by 3 to make all prime factors in pairs, i.e., 9408 × 3 = 28224, which is a square number.
Prime factorisation of 28224: 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 7 × 7
Grouping the prime factors into equal groups, we get: (2 × 2 × 2 × 3 × 7) × (2 × 2 × 2 × 3 × 7)
So, the square root of 28224 is 2 × 2 × 2 × 3 × 7 = 168.
7. How many numbers lie between the squares of the following numbers?
(i) 16 and 17
(ii) 99 and 100
Count the whole numbers between n² and (n+1)².
The count = (n+1)² – n² – 1 = 2n.
(i) Between 16 and 17
16² = 256, 17² = 289.
Numbers between them = 289 – 256 – 1 = 32.
(ii) Between 99 and 100
99² = 9801, 100² = 10000.
Numbers between them = 10000 – 9801 – 1 = 198.
Final Answer:
(i) 32 numbers
(ii) 198 numbers
8. In the following pattern, fill in the missing numbers:
Answer:
9. How many tiny squares are there in the following picture? Write the prime factorisation of the number of tiny squares.
Answer:
Number of squares in a row = 9.
Number of squares in a column = 9.
Total number of squares in the picture = 9 × 9 = 81.
Number of tiny squares in a square = 5 × 5 = 25.
Total number of tiny squares in the picture = 25 × 81 = 2025.
1.2 Cubic Numbers
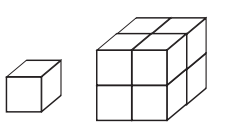
Q. How many cubes of side 1 cm make a cube of side 2 cm?
Answer:
By looking at the arrangement, we find that there are 2 × 2 unit cubes at the top layer, and there are 2 such layers.
So, a total of 2 × 2 × 2 = 8 cubes of side 1 cm make a cube of side 2 cm.
Q. How many cubes of side 1 cm will make a cube of side 3 cm?
Answer:
In the arrangement of a cube of side 3 cm, there will be 3 × 3 unit cubes at the top layer, and there will be 3 such layers.
So, there will be 3 × 3 × 3 = 27 cubes of side 1 cm that will make a cube of side 3 cm.
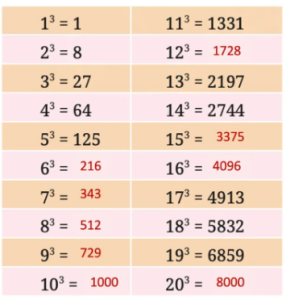
Q. Complete the table below.
Answer:
Q. What patterns do you notice in the table above?
Answer:
Observations:
Cube of a number having 0 at the units place, will have three trailing zeros.
The cube of an even number is even, and the cube of an odd number is odd.
There are only four perfect cubes up to 100 and ten perfect cubes up to 1000.
Q. We know that 0, 1, 4, 5, 6, 9 are the only last digits possible for squares. What are the possible last digits of cubes?
Answer:
Cubic numbers can end in any digit from 0 to 9, unlike square numbers.
Additionally, the cube of a number ending with 0, 1, 4, 5, 6, or 9 also ends with 0, 1, 4, 5, 6, or 9, respectively.
But the cube of a number ending with 2, 3, 7, and 8 ends with 8, 7, 3, and 2, respectively.
Q. Similar to squares, can you find the number of cubes with 1 digit, 2 digits, and 3 digits? What do you observe?
Answer:
We want to find how many perfect cubes have:
1 digit,
2 digits,
3 digits.
Cubes with 1 digit
Numbers:\(1^3\) = 1, \(2^3\) = 8.
So, only 2 cubes (1, 8).
Cubes with 2 digits
Numbers:
\(3^3\) = 27, \(4^3\) = 64, \(5^3\) = 125 (already 3 digits).
So, only 2 cubes (27, 64).
Cubes with 3 digits
Numbers:
\(5^3\) = 125 up to \(9^3\) = 729.
So cubes are: 125, 216, 343, 512, 729.
That makes 5 cubes.
Q. Can a cube end with exactly two zeroes (00)? Explain.
Answer:
No. A cube cannot end with exactly two zeros because zeros in a cube occur in multiples of three. If a number ends in one zero, its cube ends in three zeros.
Taxicab Numbers
Q. The next two taxicab numbers after 1729 are 4104 and 13832. Find the two ways in which each of these can be expressed as the sum of two positive cubes.
Answer:
1. Taxicab Number 4104
4104 can be expressed as the sum of two positive cubes in two different ways:
1. 4104 = 2³ + 16³
2³ + 16³ = 8 + 4096 = 4104
2. 4104 = 9³ + 15³
9³ + 15³ = 729 + 3375 = 4104
2. Taxicab Number 13832
13832 can also be expressed in two different ways as the sum of cubes:
1. 13832 = 2³ + 24³
2³ + 24³ = 8 + 13824 = 13832
2. 13832 = 18³ + 20³
18³ + 20³ = 5832 + 8000 = 13832
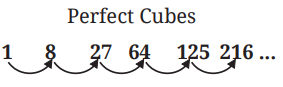
Perfect Cubes and Consecutive Odd Numbers
Q. Can you tell what this sum is without doing the calculation?
Answer:
1 = 1 = 1³
3 + 5 = 8 = 2³
7 + 9 + 11 = 27 = 3³
13 + 15 + 17 + 19 = 64 = 4³
21 + 23 + 25 + 27 + 29 = 125 = 5³
31 + 33 + 35 + 37 + 39 + 41 = 216 = 6³
We see a pattern:
The sum of the next group of consecutive odd numbers gives the next cube number.
The given set is:
91 + 93 + 95 + 97 + 99 + 101 + 103 + 105 + 107 + 109
The number of terms in the sum is 10 consecutive odd numbers.
According to the pattern, the sum of the first 10 odd numbers is 10³ = 1000.
Therefore, without calculating step by step, we can say the sum is 1000.
Cube Roots
Q. Find the cube roots of these numbers:
(i) \(\sqrt[3]{64}\) =
(ii) \(\sqrt[3]{512}\) =
(iii) \(\sqrt[3]{729}\) =
Answer:
(i) Prime factorisation of 64 = 2 × 2 × 2 × 2 × 2 × 2
This can be divided into three equal groups as
64 = (2 × 2) × (2 × 2) × (2 × 2) = (2 × 2)³
⇒ \(\sqrt[3]{64}\) = (2 × 2) = 4
(ii) Prime factorisation of 512 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
This can be divided into three equal groups as
512 = (2 × 2 × 2) × (2 × 2 × 2) × (2 × 2 × 2) = (2 × 2 × 2)³
⇒ \(\sqrt[3]{512}\) = (2 × 2 × 2) = 8
(iii) Prime factorisation of 729 = 3 × 3 × 3 × 3 × 3 × 3
This can be divided into three equal groups as
729 = (3 × 3) × (3 × 3) × (3 × 3) = (3 × 3)³
⇒ \(\sqrt[3]{729}\) = (3 × 3) = 9
Successive Differences
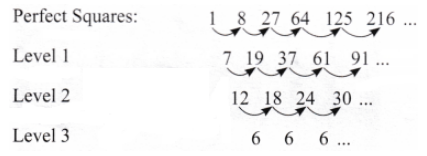
Q. Compute successive differences over levels for perfect cubes until all the differences at a level are the same. What do you notice?
Answer:
Observe the differences step by step:
- The first-level differences do not follow a specific pattern.
- The second-level differences increase by 6 each time (like 12, 18, 24, etc.).
- At the third level, all the differences become constant and equal to 6.
Thus, 6 is the constant difference found at the third level.
Figure it Out
1. Find the cube roots of 27000 and 10648.
Answer:
1. For 27000:
First, write the prime factors of 27000:
27000 = 2 × 2 × 2 × 3 × 3 × 3 × 5 × 5 × 5
Next, group the factors into three equal groups:
27000 = (2 × 3 × 5) × (2 × 3 × 5) × (2 × 3 × 5)
= (2 × 3 × 5)³
Therefore, the cube root of 27000 is:
³√27000 = 2 × 3 × 5 = 30
2. For 10648:
First, write the prime factors of 10648:
10648 = 2 × 2 × 2 × 11 × 11 × 11
Next, group the factors into three equal groups:
10648 = (2 × 11) × (2 × 11) × (2 × 11)
= (2 × 11)³
Therefore, the cube root of 10648 is:
³√10648 = 2 × 11 = 22
2. What number will you multiply by 1323 to make it a cube number?
Answer:
First, do the prime factorisation of 1323:
1323 = 3 × 3 × 3 × 7 × 7
That means: 1323 = 3³ × 7²
To make it a perfect cube, every prime factor should appear in multiples of 3.
Right now, the factor 7 appears only twice (7²).
We need one more 7 to make it a complete cube (7³).
So, multiply 1323 by 7:
1323 × 7 = (3³ × 7²) × 7 = 3³ × 7³ = (3 × 7)³ = 21³ = 9261
We should multiply 1323 by 7 to make it a cube number.
So, the required number is 7.
3. State true or false. Explain your reasoning.
(i) The cube of any odd number is even.
(ii) There is no perfect cube that ends with 8.
(iii) The cube of a 2-digit number may be a 3-digit number.
(iv) The cube of a 2-digit number may have seven or more digits.
(v) Cube numbers have an odd number of factors
(i) The cube of any odd number is even.
An odd number multiplied by itself three times (odd × odd × odd) is always odd, not even.
Example: 3³ = 27 (odd).
Answer: False
(ii) There is no perfect cube that ends with 8.
Check small cubes:
2³ = 8, ends with 8.
So, at least one perfect cube ends in 8.
Answer: False
(iii) The cube of a 2-digit number may be a 3-digit number.
Smallest 2-digit number = 10.
10³ = 1000,which is 4-digit, not 3-digit.
All larger 2-digit numbers will give cubes bigger than 1000.
Answer: False
(iv) The cube of a 2-digit number may have seven or more digits.
Largest 2-digit number = 99.
99³ = 970, 299, which has 6 digits, not 7.
So, a 2-digit cube can never reach 7 digits.
Answer: False
(v) Cube numbers have an odd number of factors.
A number has an odd number of factors only if it is a perfect square.
Example: 8 = 2³ → factors: 1, 2, 4, 8 (4 factors, even).
Cubes are not necessarily squares, so they generally have an even number of factors.
Answer: False
4. You are told that 1331 is a perfect cube. Can you guess without factorisation what its cube root is? Similarly, guess the cube roots of 4913, 12167, and 32768.
Answer:
Trick to guess cube roots without factorisation:
1. Look at the last digit of the number → it tells the last digit of the cube root.
2. Look at the remaining digits (before the last 3 digits) → this tells the first digit of the cube root by finding the nearest cube.
(1) 1331
- Last digit = 1 → cube root ends in 1.
- 1331 is a 4-digit number.
- Among cubes: 10³ = 1000, 11³ = 1331, 12³ = 1728.
So,\(\sqrt[3]{1331}\) = 11
(2) 4913
- Last digit = 3 → cube root ends in 7 (since 7³ = 343 ends in 3).
- 4913 is a 4-digit number.
- 17³ = 4913.
So,\(\sqrt[3]{4913}\) = 17
(3) 12167
- Last digit = 7 → cube root ends in 3 (since 3³ = 27 ends in 7).
- 12167 is a 5-digit number.
- 23³ = 12167.
So,\(\sqrt[3]{12167}\) = 23
(4) 32768
- Last digit = 8 → cube root ends in 2 (since 2³ = 8 ends in 8).
- 32768 is a 5-digit number.
- 32³ = 32768.
So,\(\sqrt[3]{32768}\) = 32
5. Which of the following is the greatest? Explain your reasoning.
(i) 67³ – 66³
(ii) 43³ – 42³
(iii) 67² – 66²
(iv) 43² – 42²
Answer:
Use the identities for differences:
a³ − b³ = (a−b)(a² + ab + b²). For consecutive integers a = n,b = n − 1:
n³ − (n − 1)³ = n² + n (n − 1) + (n − 1)² = 3n² − 3n + 1.
a² − b² = (a−b) (a+b). For consecutive integers a = n, b = n − 1:
n² − (n−1)² = n + (n−1) = 2n − 1.
(i) 67³ − 66³ = 3(67)² − 3(67) + 1
67² = 4489 so 3. 4489 = 13467 Then 13467 − 201 + 1 = 13267.
(i) 43³ − 42³ = 3(43)² − 3(43) + 1
43² = 1849 so 3⋅ 1849 = 5547 Then 5547 − 129 + 1 = 5419.
(iii) 67² − 66² = 2⋅ 67 − 1 = 134 − 1 = 133.
(iv) 43² − 42² = 2⋅ 43 − 1 = 86 − 1 = 85.
Therefore (i) 67³ − 66³ is the greatest.
Puzzle Time
Q. Try arranging the numbers 1 to 17 (without repetition) in a row in a similar way — the sum of every adjacent pair of numbers should be a square.
Answer:
One valid arrangement (left → right)
16, 9, 7, 2, 14, 11, 5, 4, 12, 13, 3, 6, 10, 15, 1, 8, 17
Check (every adjacent sum is a perfect square)
- 16 + 9 = 25
- 9 + 7 = 16
- 7 + 2 = 9
- 2 + 14 = 16
- 14 + 11 = 25
- 11 + 5 = 16
- 5 + 4 = 9
- 4 + 12 = 16
- 12 + 13 = 25
- 13 + 3 = 16
- 3 + 6 = 9
- 6 + 10 = 16
- 10 + 15 = 25
- 15 + 1 = 16
- 1 + 8 = 9
- 8 + 17 = 25
All sums are in the set {9, 16, 25} — so the condition is satisfied.
Q. Can you arrange them in more than one way? If not, can you explain why?
Answer:
is also valid. Apart from reversing, no other distinct arrangement exists for 1–17 (reason: the graph of allowed pairs admits essentially one Hamiltonian path).
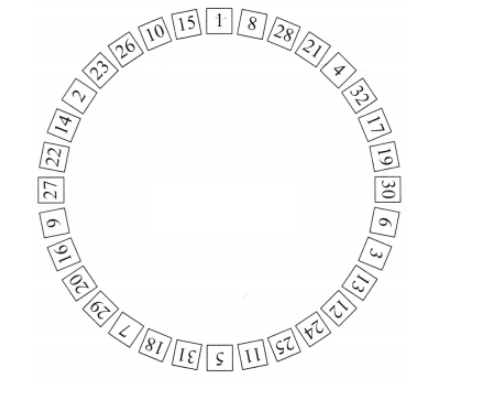
Q. Can you do the same with numbers from 1 to 32 (again, without repetition), but this time arranging all the numbers in a circle?
Answer:
Here is a complete circular arrangement of the numbers 1 to 32 so that every adjacent pair (including the last with the first) sums to a perfect square, and a quick verification.
The circle (read around the circle)
1, 8, 28, 21, 4, 32, 17, 19, 30, 6, 3, 13, 12, 24, 25, 11, 5, 31, 18, 7, 29, 20, 16, 9, 27, 22, 14, 2, 23, 26, 10, 15
(then back to 1 to close the circle)

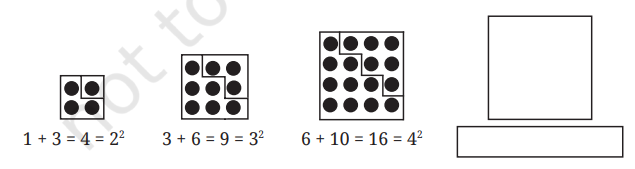
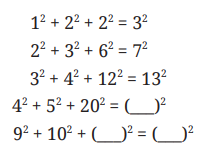
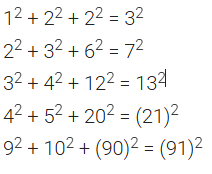



Leave a Reply