2.1 Experiencing the Power Play …
Q. Say you can fold a sheet of paper as many times as you wish. What would its thickness be after 30 folds? Make a guess.
Let us find out how thick a sheet of paper will be after 46 folds. Assume that the thickness of the sheet is 0.001 cm.
Answer:
- Initial thickness of paper = 0.001 cm
- Each fold doubles the thickness
- After n folds, thickness =
T = 0.001 × \(2^n\) cm
(A) Thickness after 30 folds
T = 0.001 × \(2^{30}\)
Now calculate:
- \(2^{10}\) = 1024 ≈ \(10^3\)
- \(2^{20}\) = (\(2^{10}\))² ≈ (\(10^3\))² = \(10^6\)
- \(2^{30}\) = (\(2^{10}\))³ ≈ (\(10^3\))³ = \(10^9\)
- Exact: \(2^{30}\) = 1,073,741,824
T = 0.001 × 1,073, 741, 824 = 1,073,741.824cm
Convert:
- 1m = 100cm
- 1,073,741.824 ÷ 100 = 10,737.418m
- 10,737.418 ÷ 1000 = 10.737km
After 30 folds, thickness ≈ 10.7 km (about the height at which planes fly).
(B) Thickness after 46 folds
T = 0.001 × \(2^{46}\)
Now calculate:
\(2^{46}\) = 70,368,744,177,664
Multiply:
T = 0.001 × 70,368,744,177,664 = 70,368,744,177.664cm
Convert:
- To meters: 70,368,744,177.664 ÷ 100 = 703,687,441.776m
- To kilometers: 703,687,441.776 ÷ 1000 = 703,687.442km
After 46 folds, thickness ≈ 7,03,687 km — more than the distance from Earth to the Moon (~3,84,400 km)!
Q. Fill the table below
Answer:
| Fold | Thickness | Fold | Thickness | Fold | Thickness |
|---|---|---|---|---|---|
| 18 | ≈ 262 cm | 21 | ≈ 20.97 m | 24 | ≈ 167.8 m |
| 19 | ≈ 524 cm | 22 | ≈ 41.9 m | 25 | ≈ 335.5 m |
| 20 | ≈ 10.4 m | 23 | ≈ 83.9 m | 26 | ≈ 670 m |
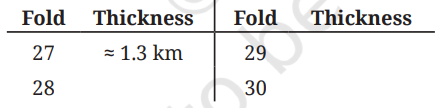
Q. After 26 folds, the thickness is approximately 670 m. Burj Khalifa in Dubai, the tallest building in the world, is 830 m tall.
Answer:
| Fold | Thickness | Fold | Thickness |
|---|---|---|---|
| 27 | ≈ 1.3 km | 29 | ≈ 5.2 km |
| 28 | ≈ 2.6 km | 30 | ≈ 10.4 km |
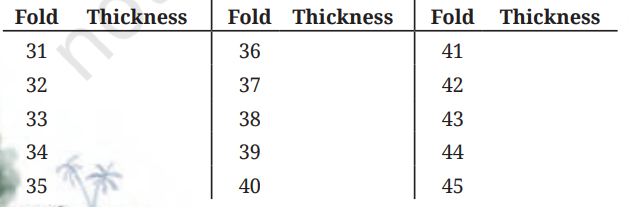
Q. After 30 folds, the thickness of the paper is about 10.7 km, the typical height at which planes fly. The deepest point discovered in the oceans is the Mariana Trench, with a depth of 11 km.
Answer:
| Fold | Thickness | Fold | Thickness | Fold | Thickness |
|---|---|---|---|---|---|
| 31 | ≈ 21.4 km | 36 | ≈ 684.8 km | 41 | ≈ 21,913.6 km |
| 32 | ≈ 42.8 km | 37 | ≈ 1369.6 km | 42 | ≈ 43,827.2 km |
| 33 | ≈ 85.6 km | 38 | ≈ 2739.2 km | 43 | ≈ 87,654.4 km |
| 34 | ≈ 171.2 km | 39 | ≈ 5478.4 km | 44 | ≈ 175,308.8 km |
| 35 | ≈ 342.4 km | 40 | ≈ 10,956.8 km | 45 | ≈ 350,617.6 km |
2.2 Exponential Notation and Operations
Q. Which expression describes the thickness of a sheet of paper after it is folded 10 times? The initial thickness is represented by the letter-number v.
(i) 10v
(ii) 10 + v
(iii) 2 × 10 × v
(iv) \(2^{10}\)
(v) \(2^{10}\)v
(vi) \(10^2\)v
Answer:
- Initial thickness = v
- Every time the paper is folded, its thickness doubles.
So, after 10 folds, the thickness becomes:
v × 2 × 2 × 2 × … (10 times) = v × 2¹⁰
The correct expression is: \(2^{10} \times v\)
Final Answer: (v) \(2^{10}v\)
Q. What is \((– 1)^5\) ? Is it positive or negative? What about \((– 1)^{56}?\)
Answer:
(i) \((– 1)^5\):
\((– 1)^5\) = – 1 × – 1 × – 1 × – 1 × –1 = – 1
Since the exponent is odd (5), the result is –1 (negative).
(ii) \((– 1)^{56}?\):
\((– 1)^{56}?\) = \((– 1 × – 1)^{28}\) = \(1^{28}?\) = 1
Since the exponent is even (56), the result is 1 (positive).
For Example :
- \((– 1)^1\) = – 1
- \((– 1)^2\) = – 1 × – 1 = + 1
- \((– 1)^3\) = – 1 × – 1 × – 1 = – 1
- \((– 1)^4\) = – 1 × – 1 – 1 × – 1 = + 1
- \((– 1)^5\) = – 1 × – 1 × – 1 × – 1 × –1 = – 1
Q. Is \((– 2)^4\) = 16? Verify.
Answer:
\((–2)^4\) = (–2) × (–2) × (–2) × (–2)
Calculation:
- (–2) × (–2) = 4
- 4 × (–2) = –8
- (–8) × (–2) = 16
So, \((–2)^4\) = 16
Yes, \((–2)^4\) = 16 is correct.
Figure it Out
1. Express the following in exponential form:
(i) 6 × 6 × 6 × 6
(ii) y × y
(iii) b × b × b × b
(iv) 5 × 5 × 7 × 7 × 7
(v) 2 × 2 × a × a
(vi) a × a × a × c × c × c × c × d
Answer:
(i) \(6^4\)
(ii) \(Y^2\)
(iii) \(b^4\)
(iv) \(5^2 × 7^3\)
(v) \(2^2 × a^2\)
(vi) \(a^3 × c^4 × d\)
2. Express each of the following as a product of powers of their prime factors in exponential form.
(i) 648 (ii) 405 (iii) 540 (iv) 3600
Answer:
(i) 648 = 2 × 2 × 2 × 3 × 3 × 3 × 3 = \(2^3 × 3^4\)
(ii) 405 = 3 × 3 × 3 × 3 × 5 = \(3^4 × 5\)
(iii) 540 = 2 × 2 × 3 × 3 × 3 × 5 = \(2^2 × 3^3 × 5\)
(iv) 3600 = 2 × 2 × 2 × 2 × 3 × 3 × 5 × 5 = \(2^4 × 3^2 × 5^2\)
3. Write the numerical value of each of the following:
(i) \(2 × 10^3\)
(ii) \(7^2 × 2^3\)
(iii) \(3 × 4^4\)
(iv) \((–3)^2 × (–5)^2\)
(v) \(3^2 × 10^4\)
(vi) \((–2)^5 × (– 10)^6\)
Answer:
(i) \(2 × 10^3\) = 2 × 1000 = 2000
(ii) \(7^2 × 2^3\) = (7 × 7) × (2 × 2 × 2) = 49 × 8 = 392
(iii) \(3 × 4^4\) = 3 × (4 × 4 × 4 × 4) = 3 × 256 = 768
(iv) \((–3)^2 × (–5)^2\) = (–3 × –3) × (–5 × –5) = 9 × 25 = 225
(v) \(3^2 × 10^4\) = (3 × 3) × 10,000 = 9 × 10,000 = 90,000
(vi) \((–2)^5 × (– 10)^6\) = \((–2)^5\) = – 32 and \((– 10)^6\) = (–10× –10 × –10 × –10 × –10 × –10) = \((10)^6\) = 1,000,000
So, –32 × 1,000,000 = –32,000,000
The Stones that Shine …
Q. \(3^7\) can also be written as \(3^2 × 3^5\). Can you reason out why?
Answer:
\(n^a × n^b = n^{a+b}\)
\(3^7 = 3^2 × 3^5\)
because according to the exponent rule, multiplying powers with the same base adds their exponents:
\(3^2 × 3^5 = 3^{2+5} = 3^7\)
Q. Use this observation to compute the following.
(i) \(2^9\)
(ii) \(5^7\)
(iii) \(4^6\)
Answer:
(i) \(2^9\) = (2 × 2 × 2) × (2 × 2 × 2) × (2 × 2 × 2) = 2³ × 2³ × 2³ = 8 × 8 × 8 = 512.
(ii) \(5^7\) = (5 × 5) × (5 × 5) × (5 × 5) × 5 = 5² × 5² × 5² × 5 = 25 × 25 × 25 × 5 = 78,125.
(iii) \(4^6\) = (4 × 4) × (4 × 4) × (4 × 4) = 4² × 4² × 4² = 16 × 16 × 16 = 4096.
Q. Write the following expressions as a power of a power in at least two different ways:
(i) \(8^6\)
(ii) \(7^{15}\)
(iii) \(9^{14}\)
(iv) \(5^8\)
Answer:
(i) \(8^6\)
1. \(8^6\) = (8³)²
2. \(8^6\) = (8²)³
(ii) \(7^{15}\)
1. \(7^{15}\) = (\(7^5\))³
2. \(7^{15}\) = \((7^3)^5\)
(iii) \(9^{14}\)
1. \(9^{14}\) = \((9^7)^2\)
2. \(9^{14}\) = \((9^2)^7\)
(iv) \(5^8\)
1. \(5^8\) = \((5^4)^2\)
2. \(5^8\) = \((5^2)^4\)
Magical Pond
In the middle of a beautiful, magical pond lies a bright pink lotus. The number of lotuses doubles every day in this pond. After 30 days, the pond is completely covered with lotuses. On which day was the pond half full?
If the pond is completely covered by lotuses on the 30th day, how much of it is covered by lotuses on the 29th day?
Since the number of lotuses doubles every day, the pond should be half covered on the 29th day.
Q. Write the number of lotuses (in exponential form) when the pond was —
(i) fully covered (ii) half covered
Answer:
Half-full day
If it doubles every day, then on the 29th day the pond must have been half full.
So, answer:
The pond was half full on the 29th day.
How much on the 29th day
Since the 30th day is full, the 29th day = half full.
Write in exponential form
Let’s assume on the first day there was 1 lotus.
On the 2nd day → \(2^1\)lotuses
On the 3rd day → \(2^2\)lotuses
…
On the 30th day → \(2^{29}\) lotuses (fully covered)
On the 29th day → \(2^{28}\) lotuses (half covered)
Q. Use this observation to compute the value of \(2^5 × 5^5\).
Answer:
\(m^a × n^a = (m×n)^a\)
This works when the exponents (powers) are the same.
Apply the rule:
Here, both have exponent 5.
\(2^5 × 5^5 = (2×5)^5\)
\(= 10^5\)
Compute the value:
\(10^5\) = 100000
\(2^5 × 5^5 = 10^5\) = 100000
Q. Simplify \(\frac{10^4}{5^4}\) and write it in exponential form.
Answer:
How Many Combinations
Q. Roxie has 7 dresses, 2 hats, and 3 pairs of shoes. How many different ways can Roxie dress up?
Answer:
If we have choices in groups, the total number of combinations =
(choices of first)×(choices of second)(choices of third)…
Number of dresses = 7
Number of hats = 2
Number of shoes = 3
So, total combinations = 7 × 2 × 3 = 42
Roxie can dress up in 42 different ways.
Q. Estu and Roxie came across a safe containing old stamps and coins that their great-grandfather had collected. It was secured with a 5-digit password. Since nobody knew the password, they had no option except to try every password until it opened. They were unlucky and the lock only opened with the last password, after they had tried all possible combinations. How many passwords did they end up checking?
Answer:
Estu and Roxie found a 5-digit lock.
- Each digit can be from 0 to 9 (10 choices).
- They had to try all possible combinations until the last one worked.
Possible choices per digit
For each digit: 10 choices.
Total combinations
10 × 10 × 10 × 10 × 10 = \(10^5\)
\(10^5\) = 100000
Estu and Roxie ended up checking 100,000 passwords.
Q. Estu says, “Next time, I will buy a lock that has 6 slots with the letters A to Z. I feel it is safer.”
How many passwords are possible with such a lock?
Answer:
Estu wants a lock with 6 slots, and each slot can have letters A–Z.
That means each slot has 26 choices.
For each slot → 26 options.
Total combinations
26 × 26 × 26 × 26 × 26 × 26 = \(26^6\)
Compute value
- \(26^2\) = 676
- \(26^3\) = 26 × 676 = 17576
- \(26^4\) = 26 × 17576 = 456976
- \(26^5\) = 26 × 456976 = 11881376
- \(26^6\) = 26 × 11881376 = 308915776
The lock can have
\(26^6\) = 308,915,776 possible passwords.
Q. Think about how many combinations are possible in different contexts. Some examples are—
(i) Pincodes of places in India—The Pincode of Vidisha in Madhya Pradesh is 464001. The Pincode of Zemabawk in Mizoram is 796017.
(ii) Mobile numbers.
(iii) Vehicle registration numbers.
Try to find out how these numbers or codes are allotted/generated
Answer:
(i) PIN Codes in India
India uses a 6-digit Postal Index Number (PIN) system introduced in 1972.
Structure:
- 1st digit: Region (9 zones total)
- 2nd digit: Sub-region
- 3rd digit: Sorting district
- Last 3 digits: Specific post office
Combinations:
- Theoretically: \(10^6\) = 1,000,000 combinations
- Practically: Only valid combinations are used based on geography and postal infrastructure.
e.g, 464001 → Vidisha, Madhya Pradesh
796017 → Zemabawk, Mizoram
(ii) Mobile numbers in India
Indian mobile numbers are 10 digits, starting with digits 6-9.
Structure:
- 1st digit: Must be 6, 7, 8, or 9
- Remaining 9 digits: Any number from 0-9
Combinations:
\(4 × 10^9\) = 4,000,000,000 possible mobile numbers
Allocation:
- Managed by the Department of Telecommunications
- Prefixes (like 91x, 98x) are assigned to different telecom operators.
(iii) Vehicle Registration Numbers
Vehicle numbers follow a format like DL 01 AB 1234.
Structure:
- 2 letters: State/UT code (e.g., DL for Delhi)
- 2 digits: RTO code
- 1-2 letters: Series
- 4 digits: Unique vehicle number
Combinations:
Varies by state and RTO, but for one RTO:
\(26^2\) letter combinations × \(10^4\) numbers = 676 × 10,000 = 6,760,000 combinations per RTO
Allocation:
- Managed by the Ministry of Road Transport & Highways via the Parivahan portal.
- Fancy numbers can be bid for, and older vehicles may require re-registration.
2.3 The Other Side of Powers
Q. What is \(2^{100} ÷ 2^{25}\)in powers of 2?
Answer:
Q. In a generalised form, \(n^a ÷ n^b = n^{a-b},\) where n ≠ 0 and a and b are counting numbers and a > b. Why can’t n be 0?
Answer:
What if n = 0?
Take an example: \(0^4 ÷ 0^2\)
This means:
\(\frac{0 × 0 × 0 × 0}{0 × 0}\)
Here, the denominator becomes 0. But division by zero is not defined in mathematics.
If n = 0, then in any expression like
\(0^a ÷ 0^b\)
the denominator will always be \(0^b = 0.\)
Since dividing by zero has no meaning, the formula cannot work.
That’s why the rule explicitly states 𝑛 ≠ 0
This keeps the denominator nonzero and ensures the expression makes sense.
We cannot take n = 0 because then the denominator becomes 0 (like \(0^b\)), and division by zero is not possible. Therefore, the formula \(n^a ÷ n^b = n^{a-b}\) is valid only when 𝑛 ≠ 0.


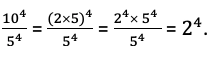

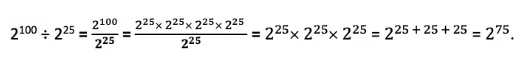

Leave a Reply